空间非合作目标质量特性在轨辨识*

张海博 王大轶 魏春岭

1.北京控制工程研究所，北京100190

2.空间智能控制工程技术重点实验室，北京100190

空间操作作为未来航天技术发展的方向，越来越受到航天大国的重视［1］。利用空间机器人携带的机械臂对目标(失效目标)进行捕获，进一步进行维护或者离轨操作，可产生巨大的经济效益。当机械臂捕获未知目标时，系统在捕获前后动力学特性参数可能会发生相当大的变化。为保证系统的控制性能，必须对未知目标的质量特性参数，包括质量、质心和转动惯量进行在线辨识。

对于空间机器人系统来说，在忽略系统所受到的小量外力和外力矩的情况下满足角动量和线动量守恒定理，由此，许多文献研究了基于角动量守恒和线动量守恒的质量特性参数辨识。文献［2］首先提出了基于线动量守恒定理辨识空间机器人本体惯性参数的算法，但该方法不能独立的获得质量和转动惯量参数。文献［3］针对单臂自由飞行空间机器人在其机械臂末端作用器抓住未知目标后，假设系统角速度、线速度、各关节转角和角速度信息均可测，由此采取合适的计算方法可解出未知目标的质量、质心和转动惯量参数。文献［4］基于文献［2］的基本思想，研究了双臂空间机器人负载的惯性参数是未知的情况，给出了双臂空间机器人捕获未知目标的参数辨识方法，同时该方法也可以用于本体的惯性参数辨识。文献［5］也利用角动量守恒定理，在无需力矩和加速度信息的情况下，利用机械臂各关节和本体的角速度信息，计算得到包括本体在内的整个空间机器人系统的质量和惯性矩参数。基于角动量守恒和线动量守恒的参数辨识方法原理简单，计算量小易于在线辨识。但是在辨识过程中假设系统不受外力和外力矩的作用，在实际空间环境中，由于空间干扰力和干扰力矩的存在，系统的动量、角动量是不守恒的，因此也影响了辨识的准确性。另外，辨识算法需对各关节实施驱动力矩，增加了算法的实施复杂性。文献［6］用空间机器人运动学方程来进行系统的参数辨识。不过其主要缺点在于它需要测量各关节的加速度信号，这在实际中是不可取的，因此使用方面受到很大影响。文献［7-8］基于系统的牛顿-欧拉动力学方程进行系统参数辨识，但必须已知系统受到的力和力矩，实际上进行在轨辨识时，系统受到的力和力矩是很难进行测量的。另一方面，此法已成熟地应用在以单刚体为模型的航天器质量特性参数的研究上。文献［9］提出了一种使用高斯二阶滤波的辨识方法，该方法像扩展卡尔曼滤波，但算法更复杂，计算量也更大，而且辨识模型忽略了角速度耦合项，因此要求空间机器人的运动速度足够慢，否则辨识精度不满足要求。文献［10］提出了一种针对自旋卫星的最小二乘辨识算法。文献［11］提出了以飞轮控制作为激励方式的空间机器人整体系统的质量特性。文献［12］也采用此法对小卫星进行了质量特性参数在轨辨识。文献［13］将动力学方程看作约束条件，将辨识问题转化为非线性优化问题，采用基于粒子群的优化算法辨识航天器的质量、质心和惯量参数，不过该方法仅适合于离线辨识。

本文基于系统动力学方程，在机械臂对非合作目标捕获后，通过固定机械臂构型，利用喷气激励的方式，使用递推最小二乘算法实现对整个空间机器人系统的质量参数进行辨识，进一步通过几何关系解算得到机械臂末端作用器与非合作目标联合体的质量特性。

1 空间机器人质量特性参数辨识

空间机器人系统由n自由度机械臂和作为其基座的航天器平台组成。当未知目标被机械臂牢牢抓住后，未知目标的相对位姿对于该机械臂不再改变，即该机械臂的最后一个连杆(末端作用器)和目标可看作一个整体，形成一个新的未知目标系统。以刚体的系统动力学方程作为模型进行辨识，必须通过喷气对系统进行控制，根据作用效果辨识模型中的质量、质心位置和惯量参数。动力学方程包括平动动力学方程和转动动力学方程。由平动动力学方程(即利用加速度计测量模型)辨识出系统的质量和质心位置，由转动即姿态动力学方程辨识出系统的质心位置和惯量参数。

1.1 基于加速度计测量的质量和质心辨识

1.2 基于姿态动力学方程的质心和惯量参数辨识

式中，L为推力器的安装位置，C为推力器的推力方向，质心体现在L中。F为推力器的推力大小。文中不考虑推力器的瞬时特性，即上升、下降和延迟，实际工程中该特性可根据推力器的参数进行标定。

设各推力器安装位置在空间机器人本体机械坐标系下表示为rc和L0，一般情况下，该固连坐标系选为空间机器人的机械坐标系。由几何关系

注1:上述方程中的角加速度可通过角速度差分得到或者通过滤波器得到。

1.3 基于递推最小二乘算法的在线辨识

本文采用递推最小二乘算法实现质量参数的在线辨识，该算法计算量小，运行速度快且代码占用空间率小，同时辨识的精度较高。

进一步，为了实现在线实时辨识，采用最小二乘的递推形式。递推最小二乘估计从每次获得的测量值中提取被估计量信息，用于修正上一步所得的估计值，获得测量的次数越多，修正的次数也越多，估计值的精度也越高。

基于卡尔曼滤波原理，给出加权最小二乘递推算法的过程。设X为待测量，Zi为第i次测量，量测方程为

2 非合作目标质量特性解算

采用第1节的辨识算法得到的是空间机器人抓捕非合作目标后整体的质量特性参数，而辨识的目的是得到目标的质量特性参数，准确的说是空间机器人机械臂末端作用器与目标联合体的质量特性参数。根据多体动力学的建模方法，在给定空间机器人平台以及机械臂的结构参数后，平台以及机械臂各关节的质量特性参数均可计算得到，因此在得到整体的质量特性参数后，利用几何关系进行解算来得到末端作用器与目标联合体的质量特性参数。

2.1 变量定义

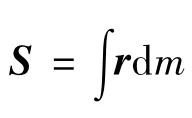
2.2 目标质量特性解算

这样结合式(24)和(25)，由式(21)、(23)和(26)可计算得到末端作用器与目标联合体的质量特性参数。

3 仿真分析

为了保证推力器的开启对空间机器人本体姿态的影响尽量小，仿真中各轴仅选取单个推力器开启，此种方式既保证了星体有一定的位置偏移，又有一定的姿态转动。该方案试验开始时，机械臂各关节锁死，本体姿态停控，设置推力器开机指令。仿真持续20s，仿真步长 1s。

推力器的选择要适中，产生的激励过大容易引起挠性部件的颤振，过小辨识精度较低。根据推力器的配置，仿真中选择推力器B4，B6，C10，推力器B6和C10的推力器大小为1.2N，B4的推力大小为5N。根据推力器的安装矩阵可知，3组推力器产生的力矩如表1所示。

表1 推力器力与力矩大小

注2:用推力器进行开环仿真时，空间机器人本体角速度不超过2(°)/s。

根据机械臂各关节的参数、空间机器人本体的质量参数以及目标的质量特性参数，经过几何计算得到组合体的质量特性参数如表2所示。仿真结果如图1～4所示。

表2 组合体的质量特性参数

图1 整体姿态角速度变化曲线

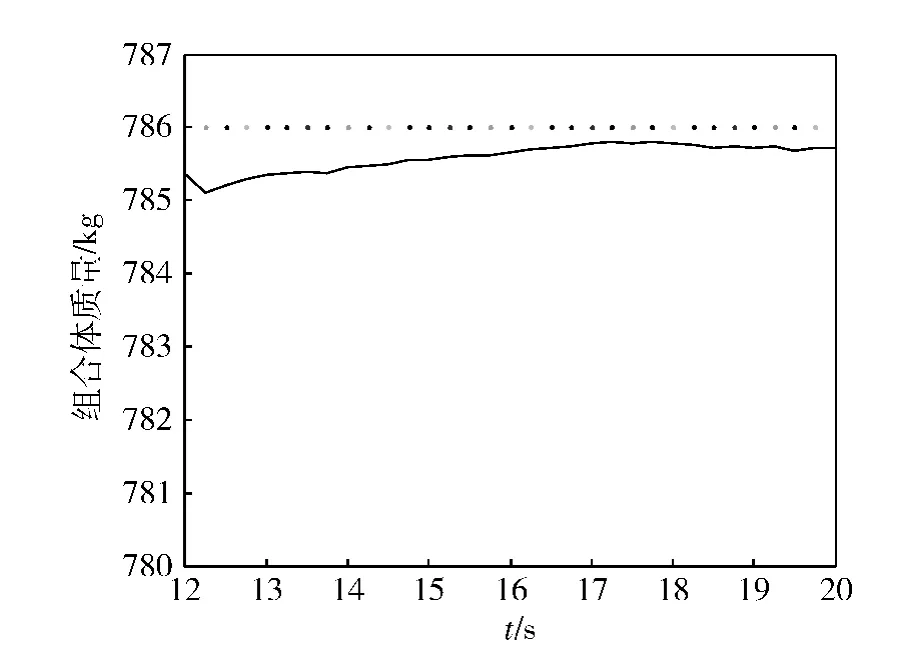
图2 整体质量辨识曲线

图3 整体质心辨识曲线

由图1可知，该试验过程中本体的姿态角速度未超过规定的范围，方案可行。由图2可知，对整体质量的辨识满足要求。由图3可知，对整体的质心辨识结果中较标称值有20mm的误差，满足要求。由图4可知，对整体主惯量的辨识结果较为准确，对惯量积的辨识结果有一定的误差，在可接受的范围内。对目标和末端作用器联合体的质量特性参数的解算过程如第2节所示，这里不再赘述。对整体的质量特性参数辨识正确，那么也可正确解算目标与末端作用器联合体的质量特性参数，方便后续控制器的设计。

图4 整体惯量辨识曲线

4 结论

针对空间非合作目标质量特性辨识问题，讨论了系统质量特性参数辨识的基本原理与方法，从辨识结果解算出末端作用器与目标联合体的质量特性参数。首先建立了基于加速度计测量模型和基于系统姿态动力学模型的整体质量特性参数辨识方法，采用递推最小二乘法实现辨识。然后给出了解算目标特性参数的算法，最后仿真说明了算法的有效性。

［1］ 何英姿，魏春岭，汤亮.空间操作控制技术研究现状及发展趋势［J］.空间控制技术与应用，2014，40(1):1-8.(HE Yingzi，WEI Chunling，TANG Liang.A Survey on Space Operations Control［J］.Aerospace Control and Application，2014，40(1):1-8.)

［2］ Murotsu Y，Tsujio S，et al.System Identification and Resolved Acceleration Control of Space Robots by Using Experimental System［C］//Proceedings of the IEEE/RSJ International Workshop on Intelligence for Mechanical Systems.USA:IEEE，1991:1669-1674.

［3］ Murotsu Y，Senda K，et al.Parameter Identification of Unknown Object Handled by Free-Flying Space Robot［J］.Journal of Guidance，Control，and Dynamics，1994，17(3):488-494.

［4］ GUO Qi，HONG Bingrong.Parameter Identification of Unknown Object Handled By a Dual-arm Four-Degreeof-Freedom Space Robot［J］.Robot，2005，27(6):512-516.

［5］ Kazuya Y，Satoko A.Inertia Parameter Identification for a Free-Flying Space Robot［C］//AIAA Guidance，Navigation，and Control Conference.Monterey，CA，USA，5-8 August，2002.

［6］ Kawasaki H.Trajectory Control of Manipulators by On-Line Parameter Identification［J］.Transactions of Society of Instrument and Control Engineers，1984，20(9):780-787.

［7］ Atkeson C G，Hollerbach J M.Estimation of Inertial Parameters of Manipulator Loads and Links［J］.The International Journal of Robotics Research，1986，5(3):101-119.

［8］ Bergmann E，Dzielski J.Spacecraft Mass Property Identification with Torque-Generating Control［J］.Journal of Guidance，Control，and Dynamics，1990，13(1):99-103.

［9］ Sergei T，Trevor W.Mass Property Estimation Using Coasting Maneuvers［J］.Journal of Guidance，Control，and Dynamics，1997，20(4):625-632.

［10］ Edward W，David W S，Robert W M.Motion-Based Mass-And Thruster-Property Identification for Thruster-Controlled Spacecraft［C］//AIAA Aerospace Conference in Arlington.VA，USA，26-29 September，2005.

［11］ 王超，杜小平，高永明.基于飞轮控制的空间机器人质量参数辨识［J］.航天控制，2012，30(3):51-55.(WANG Chao，DU Xiaoping，GAO Yongming.Identification of Inertia Properties of Space Robot Based on Wheel Control［J］.Aerospace Control，2012，30(3):51-55.)

［12］ 徐文福，何勇，王学谦，等.航天器质量特性参数的在轨辨识方法［J］.宇航学报，2010，31(8):1906-1914.(XU Wenfu，HE Yong，WANG Xueqian，et al.On Orbit Identification of Mass Characteristic Parameters for Spacecraft［J］.Journal of Astronautics，2010，31(8):1906-1914.)

［13］ 金磊，徐世杰.空间机器人抓取未知目标的质量特性参数辨识［J］.宇航学报，2012，33(11):1570-1576.(JIN Lei，XU Shijie.Inertial Parameter Identification of Unknown Object Captured by a Space Robot［J］.Journal of Astronautics，2012，33(11):1570-1576.)