基于ESO的高超声速飞行器模糊自适应姿态控制*

胡超芳 刘运兵

天津大学电气与自动化工程学院，天津300072

高超声速飞行器是指飞行速度超过5倍声速的飞行器。由于其飞行速度快、突防能力强，因此无论在军事还是民用上都具有很高的研究价值。在再入飞行过程中，飞行包络大，气动特性变化剧烈，因此模型耦合性更强，非线性程度更高，控制起来难度也更大。而且通常无法获知精确模型参数，所以线性控制方法往往很难达到期望的性能。如Agustin等［1］曾指出，从离轨到着陆的整个再入过程中飞行器的系统结构和参数将随马赫数变化发生剧烈变化，可能导致预置增益控制器的失效。近年来，飞行器再入过程的非线性控制方法取得了一定进展。如韩钊等［2］对带有输入干扰的系统，基于多时间尺度设计了终端滑模控制律，降低了高频噪声对系统性能的影响。Lian等［3］针对再入飞行器，利用自适应反步法设计了姿态控制器。史震等［4］基于非零和博弈理论对再入飞行器设计了模糊自适应控制器，有效抑制了参数摄动对控制性能的影响。

文中针对具有耦合影响、参数摄动及输入力矩扰动情况下的六自由度再入飞行器模型，提出了基于ESO的模糊自适应姿态控制策略。首先，基于反步控制思想对简化后的面向姿态控制模型设计姿态控制系统。在此框架下，对于姿态角动态中的耦合不确定性，采用模糊自适应进行在线逼近。同时，为避免控制过程中的复杂计算，对于角速率动态中参数摄动和输入力矩扰动引起的综合不确定项，采用ESO进行在线观测并补偿。最后，为了避免反步法中虚拟控制输入求导带来的微分爆炸问题，采用了动态面策略设计控制器。基于Lyapunov的稳定性分析证明了闭环控制系统的半全局一致最终有界性，仿真结果验证了该方法的性能。

1 高超声速飞行器再入模型描述

1.1 再入模型

考虑高超声速飞行器的十二状态六自由度动态模型，由三自由度的质心平动方程和三自由度绕质心转动的角运动方程组成［5-7］，如下所示:

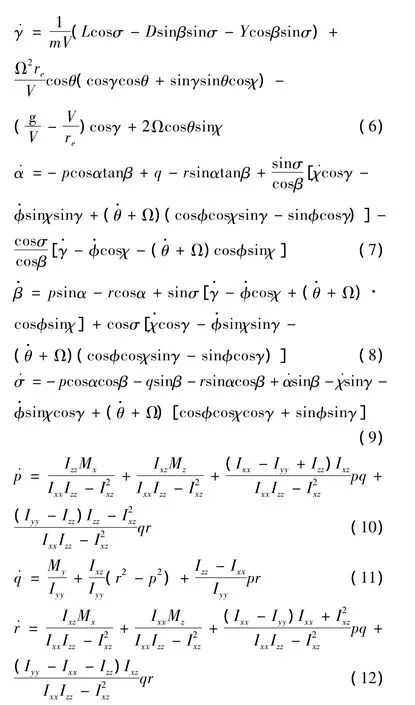
其中，re为飞行器到地心的距离，φ为经度，θ为纬度，V为飞行器的速度，χ为航向角，γ为航迹角;α，β，σ 分别代表攻角、侧滑角和倾侧角;p，q，r分别代表滚转、俯仰、偏航角速率;Ω为地球自转角速度，g 为引力加速度;Iij(i=x，y，z，j=x，y，z)为转动惯量，Mi(i=x，y，z)为滚转、俯仰和偏航通道的控制力矩;L，Y，D分别表示升力、侧力和阻力，具体形式可参见文献［8］。

1.2 面向姿态控制模型

质心平动模型式(1)～(6)主要用于轨迹优化和制导，而角运动模型式(7)～(12)则用于姿态控制。由式(7)～(9)可知姿态角运动受平动动态影响，因此为简化控制器设计，将地球自转以及飞行器自身平动对姿态运动的耦合影响作为不确定性处理，则姿态角动态式(7)～(9)可改写为如下形式:

2 姿态控制器设计及稳定性分析

2.1 姿态控制器设计

为使飞行器姿态角动态跟踪期望指令Θd=［αd，βd，σd］T，针对模型式(18)，基于动态面原理，设计姿态控制器。首先，给出如下引理和假设:

其中，x= ［x1，...，xn］T;θ为参数向量;ξ(x)为模糊基函数向量，其每个分量可表示为

设Step 1中的Lyapunov函数为:

Step 2:在模型(18)的角速率动态中，由于Δg是由参数摄动和力矩扰动产生的综合不确定项，且与ω，˙ω等多个变量均相关，若使用模糊自适应则会导致在线识别参数过多，从而造成系统运行缓慢，因此本文利用ESO来在线识别Δg。设ESO对Δg进行在线观测获得的估计值向量为Δ∈R3，本节在设计控制器时将直接使用观测值Δ，而观测器的具体设计方法以及有界性分析将在下一小节中加以阐述。

对Step 1中已定义的角速率跟踪误差z2=ωωd求导可得:

2.2 ESO设计及其误差有界性分析

3 仿真结果

应用所提方法针对X-33飞行器模型进行数值仿真，初始条件为:re=21162900，V=24061，φ=0°，θ=0°，χ=0°，α =12.6°，β =-11.46°，γ =-1.046°，σ =-57.29°，p=q=r=0(°)/s。其它参数详见文献［2］。期望攻角和倾侧角指令分别为幅值10°和40°的方波信号，而期望侧滑角为0°的阶跃信号，且均经过一阶滤波器给出。模型中的参数摄动范围以及输入扰动形式如下［7］:

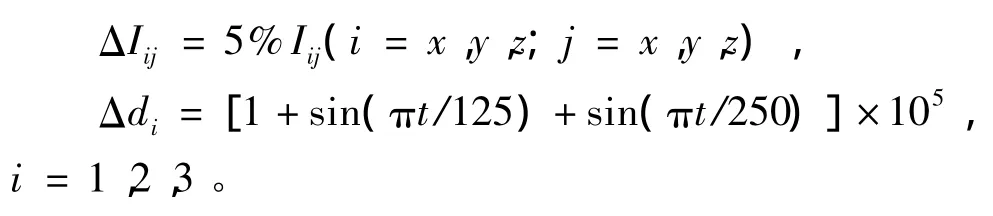
仿真中采用以高斯型隶属度函数为主的模糊系统来逼近不确定项Δf，控制参数设计为:

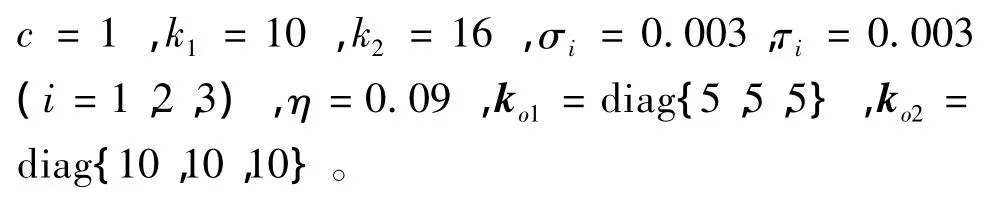
姿态控制结果如图1～2所示，从图1中看出，控制器的设计能使角动态准确跟踪姿态角指令，误差在可允许的范围内。图2表明，控制力矩幅值变化比较合理，系统稳定时能保证其处于零值附近。观测器的观测曲线如图3所示。由图可知，使用ESO可以使观测状态准确跟踪原系统状态，因此扩张状态Δ可以准确逼近不确定项Δg。综上所述，本文所设计的控制器可确保高超声速飞行器再入过程中控制系统具有良好的跟踪性能和稳定性。

图1 姿态角跟踪曲线

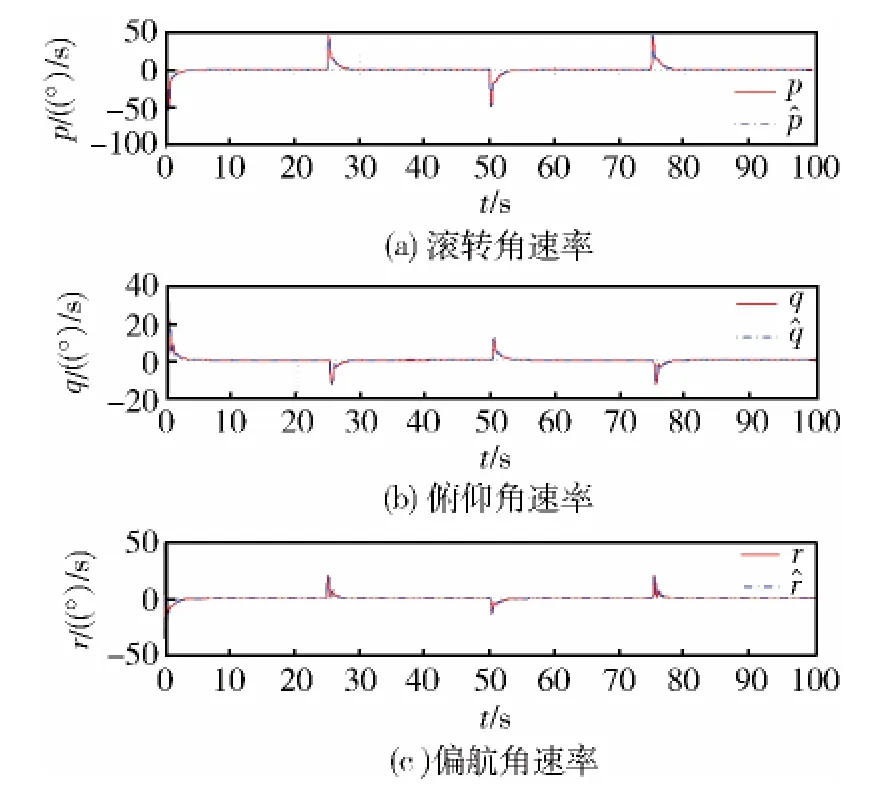
图2 姿态角速率观测曲线

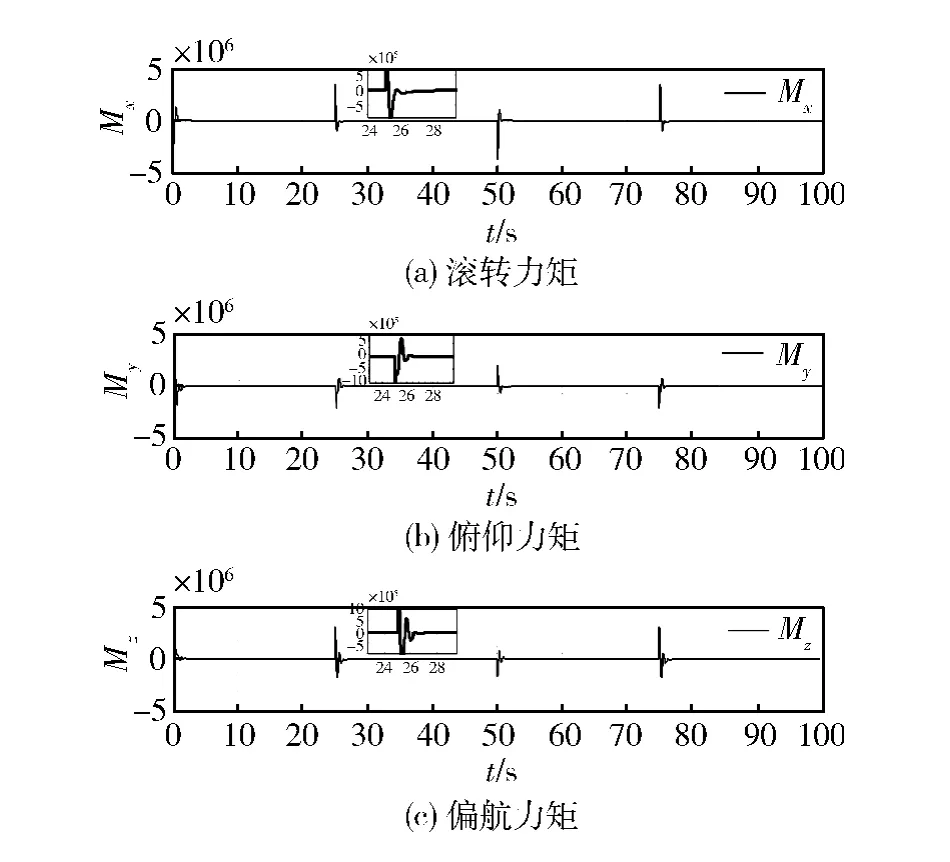
图3 控制力矩输入曲线

4 结论

针对具有耦合影响、参数摄动和输入扰动的高超声速飞行器再入模型，提出了基于ESO的模糊自适应姿态控制方法。在利用动态面策略抑制反步法微分爆炸问题基础上，除采用模糊自适应机制逼近姿态角动态的耦合不确定性外，还采用了ESO在线观测角速率动态中的综合不确定项，大大减轻了自适应计算负担。该方法不仅实现了高超声速飞行器再入姿态角的准确跟踪，而且保证了闭环系统信号的半全局一致最终有界性。

［1］ Agustin R M，Mangoubi R S，Hain R M.Robust failure detection for reentry vehicle attitude control system［J］.Journal of Guidance，Control，and Dynamics，1999，22(6):839-845.

［2］ 韩钊，宗群，田柏苓，等.基于Terminal滑模的高超声速飞行器姿态控制［J］.控制与决策，2013，28(2):259-268.(HAN Z，ZONG Q，TIAN B L，et al.Hypersonic vehicle attitude control using terminal sliding mode control［J］.Control and Decision，2013，28(2):259-268.)

［3］ Lian B H，Bang H，Hurtado J E.Adaptive backstepping control based autopilot design for reentry vehicle［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit.Rhode Island，2004.

［4］ 史震，张玉芳，王飞.再入机动飞行器的模糊自适应H2/H∞控制［J］.控制与决策，2013，28(9):1365-1371.(SHI Z，ZHANG Y F，WANG F.Fuzzy adaptive H2/H∞control for maneuvering reentry vehicle［J］.Control and Decision，2013，28(9):1365-1371.)

［5］ Desai P N，Conway B A.Six-degree-of-freedom trajectory optimization using a two-timescale collocation architecture［J］.Journal of Guidance，Conteol，and Dynamics，2008，31(5):1308-1315.

［6］ Shaffer P J.Optimal trajectory reconfiguration and retargeting for the X-33 reusable launch vehicle［D］.Monterey，California， American:Naval Postgraduate School，2004.

［7］ 王芳，宗群，田柏苓，等.基于鲁棒自适应反步的可重复使用飞行器再入姿态控制［J］.控制与决策，2014，29(1):12-18.(WANG F，ZONG Q，TIAN B L，et al.Robust adaptive back-stepping flight control design for reentry RLV ［J］.Control and Decision，2014，29(1):12-18.)

［8］ Bollino K P.High-fidelity real-time trajectory optimization for reusable launch vehicles［D］.Monterey，California，American:Naval Postgraduate School，2006.

［9］ Tong S C，He X L，Li Y M.Adaptive fuzzy backstepping robust control for uncertain nonlinear systems based on small-gain approach ［J］.Fuzzy Sets and Systems，2010，161(6):771-796.

［10］ 胡超芳，刘艳雯.基于动态面的高超声速飞行器模糊自适应非线性控制［J］.控制与决策，2013，28(12):1849-1854.(HU C F，LIU Y W.Fuzzy adaptive nonlinear control based on dynamic surface control for hypersonic vehicle ［J］.Control and Decision，2013，28(12):1849-1854.)

［11］ 李铁山，邹早建，罗伟林.基于DSC后推法的非线性系统的鲁棒自适应 NN控制［J］.自动化学报，2008，34(11):1424-1430.(LI T S，ZOU Z J，LUO W L.DSC-backstepping based robust adaptive NN control for nonlinear systems ［J］.Acta Automatic Sinica，2008，34(11):1424-1430.)

［12］ 韩京清.一类不确定对象的扩张状态观测器［J］.控制与决策，1995，10(1):85-88.

［13］ 韩京清，王伟.非线性跟踪-微分器［J］.系统科学与数学，1994，14(2):177-183.

［14］ 陈增强，孙明玮，杨瑞光.线性自抗扰控制器的稳定性研究［J］.自动化学报，2013，39(5):574-580.(CHEN Z Q，SUN M W，YANG R G.On the stability of linear active disturbance rejection control［J］.Acta Automatic Sinica，2013，39(5):574-580.)