地球-火星之间的往返轨迹全局一体化优化设计

姬聪云 南 英 安 彬 陈昊翔

南京航空航天大学航天学院，南京210016

进入21世纪，以火星，小行星为牵引的探测计划即将拉开序幕。火星是地球的近邻，它的特征在很多方面都与地球极为相似，是太阳系八大行星之一，按离太阳由近及远的次序排列为第4。火星对于人类有一种特殊的吸引力，因为它是太阳系中最近似地球的天体，它的赤道平面与公转轨道平面交角非常接近于地球，这使它也有类似地球的四季交替，同时，火星的自转周期为24小时37分，火星上的一天几乎和地球上一样长。

有人认为，火星的现在就是地球的未来。因而开展火星探测和研究，对于认识人类居住的地球环境，特别是认识地球的长期演化过程，具有十分重要的意义［1］。从1965年的“水手4号”探测器到2012年的“好奇号”火星探测器登陆火星，美国在火星探测方面已具有很强的优势。而轨迹优化是星际往返问题(火星探测)中至关重要的一步，牵涉到飞行器各种功能的实现和指标任务的达成，NASA已经确定了把轨迹优化技术作为下一代多级重复使用航天器能否成功的一个关键技术［2］。

关于地球-火星往返轨迹优化的论文并不多见，由文献［3-4］可以看出，这些论文都只对由地球到火星的单程飞行轨迹进行优化，而且性能指标也比较单一(飞行时间或者燃料消耗量)，但是在真实飞行环境下，必须考虑使飞行时间最短和燃料消耗量最少的控制条件。另外，随着深空探测技术的日趋成熟，未来还要考虑探测器返回地球的轨迹优化。美国近四十年的实验研究与实践已积累了丰富的经验，对未来的飞行器设计已经拥有较为具体的蓝本;我国在本世纪初开始了火星探测的规划，并已经实施。因此，本文以美国NASA火星探测器为飞行器模型，结合我国的航天任务需求，起飞地点等实际情况，采用一种组合优化算法对整个火星探测的飞行轨迹(包括从地球到火星的飞行轨迹和从火星返回地球的飞行轨迹)进行了全局一体化优化设计。该组合算法包括静态参数和动态参数优化方法。静态参数优化采用遗传算法，动态参数优化采用原始自然算法。

1 问题描述

2015年4月1日至2017年4月1日，将火星探测器从地球发射，在尽可能短的时间内到达火星，在火星探测工作1至2年时间，然后返回地球。

航天器的初始质量m=1500kg，推进器比冲Isp=3000s，推进的速度方向可以任意设定，推进器的开关时间和次数没有限制。

航天火星探测轨迹优化是一个多目标优化问题，优化目标主要有:1)在火星驻留时间最长;2)飞行过程中所耗的燃料最省;3)往返飞行时间最短。航天器深空探测任务中在火星周围驻留的时间越长，能够使航天器上的有效载荷工作时间最长，获得更多的有用信息数据;航天器飞行过程中所消耗的燃料越少，所耗费的成本越少，航天器之后也能进行更多的其它探索任务;往返飞行时间短可以使航天器所获得的数据尽快传送到地面研究人员手中，尽可能缩短人类探索太空的时间。

但是，显然以上3个优化目标并不能同时达到，需要优化设计一整套飞行程序，使得以下综合性能指标式(4)～(10)达到最优［5-7］，即:

飞行器最大可用推力:TMax=0.2N;飞行器离开行星时的最大可用速度差:ΔVMax=1.21 km/s，在离开地球和火星时，飞行器加速需要消耗一定的燃料，本问题中不作考虑，由其它子系统提供;ΔVM，f与ΔVE，f分别是到达火星与地球时相对火星与地球的速度 限 制［8-9］，ΔVM，f，Max=4.0km/s，ΔVE，f，Max=11.0km/s。

由式(1)可得，要使性能指标最大，航天器与火星交会时的误差(dr，dv)最小，航天器返回地球时的剩余质量mf最大，任务飞行时间t1最短，同时航天器留在火星探测的时间t2最长。

在J2000坐标系中，地球和火星绕太阳运行采用多体动力学运动微分方程:

2018年作为改革开放40周年，从青砖黛瓦到高楼大厦，从绿皮火车到高铁飞机，在中国拥抱世界的这四十年间，让中国各行业翻开新的篇章。作为一名工业媒体人， 更是感叹我国从工业化水平低到世界制造大国，完成现代化工业的华丽转身。在飞速发展的阶段，总会有一些契机，来让我们思考未来的方向。

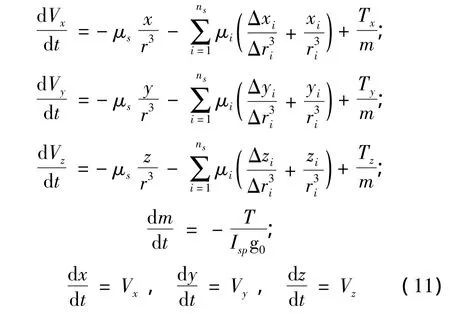
式中，(Vx，Vy，Vz)为探测器的飞行速度，(x，y，z)为探测器的3个直角坐标，(xi，yi，zi)为第 i颗行星的3 个直角坐标，(Δxi，Δyi，Δzi)为第 i颗行星与探测器的坐标值之差;r为探测器与太阳间的距离，Δri为飞行器与第i颗行星的距离;T(Tx，Ty，Tz)为探测器的控制推力，m为探测器的质量，Isp为发动机的比冲，g0=9.81m/s2;ns是所涉及到的行星个数，μs是太阳引力常数，μi是第i颗行星的引力常数。

2 轨迹优化方法

轨迹优化算法采用组合优化算法，优化算法的组合方式参见文献［10-12］，关于组合优化算法优化程序中用到的静态参数与动态参数优化算法分别是:1)静态参数的迭代优化算法为改进遗传算法，计算步骤参见文献［13］;

2)动态参数的迭代优化算法为原始的自然算法［14］。

原始的自然算法的优化设计计算步骤共分N+1步，在文献［14］的物质普适性算法基础上进行简化，与文献［14］的计算步骤类同，具体的算法步骤如下:

第1步:计算t=t0～t1的轨迹，求从第0时段到第1时段最优控制u*(0)，从起点X(0)=X0出发，求第1时段最优控制u*(1)

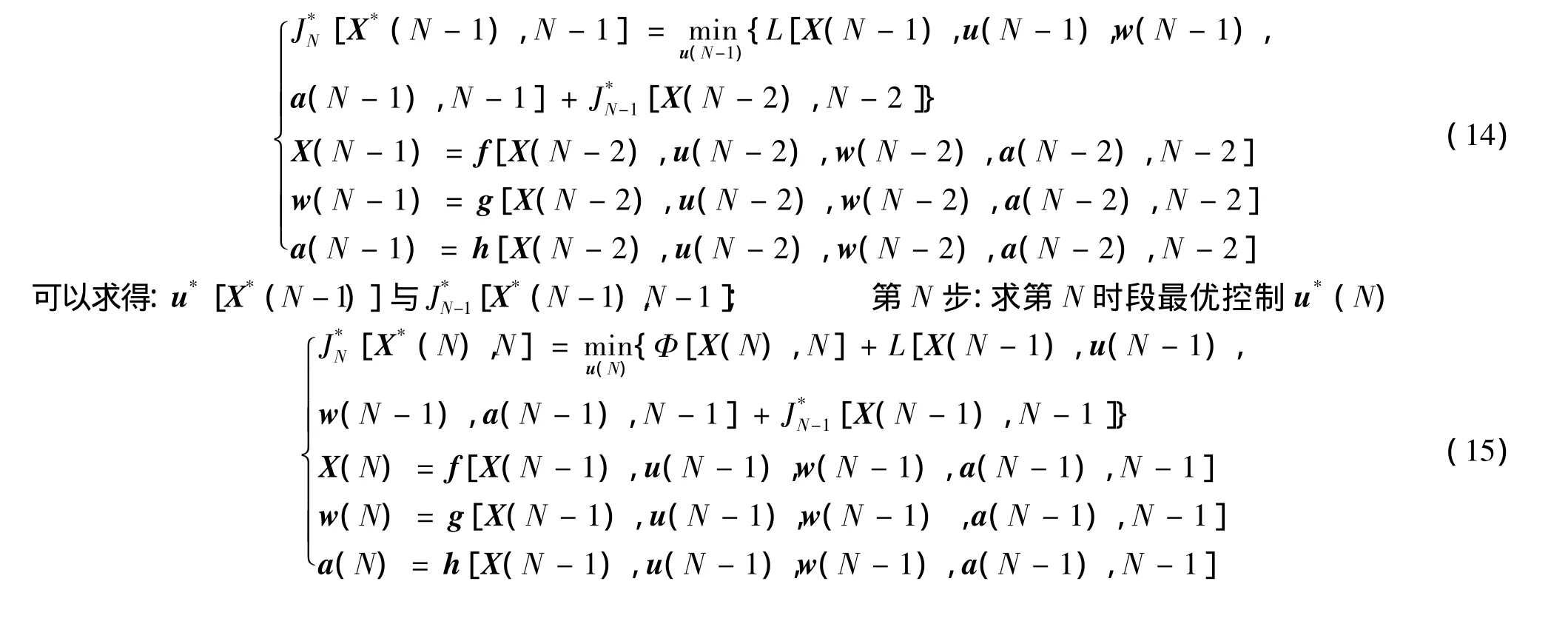
在自然计算的飞行仿真过程中，淘汰大量飞行方案，继承进化了许多相对“优化”的方案，详细的计算步骤与逻辑框图参见文献［14］。

3 仿真结果及分析

针对所提出的问题式(1)～(11)，采用飞行轨迹的组合优化算法，经过大规模的飞行优化数值仿真，得到一套最优的地-火往返飞行方案如下。

3.1 飞行仿真的结果

3.1.1 探测器从地球飞向火星

飞行器从地球出发到达火星的最优4-D飞行轨迹、速度—飞行时间、飞行器质量—飞行时间、推力控制—飞行时间分别见图1～4。

图1 探测器从地球到火星的最优飞行轨迹

3.1.2 经过近500d在火星上的探测，探测器从火星返回地球

飞行器从火星返回地球的最优4-D飞行轨迹、速度—飞行时间、飞行器质量—飞行时间和推力控制—飞行时间分别见图5～8。

3.2 仿真结果分析

图2 探测器出发后速度随时间的变化

图3 探测器出发后质量随飞行时间的变化

经过大规模(静态参数与动态参数组合优化的迭代)数值仿真，优选出一套最优飞行方案，该方案达到了在火星上探测时间的长度、往返的飞行时间、所耗发动机燃料的综合性能指标最优，同时也满足全部的约束条件。另外，由于多个性能指标是通过加权系数来综合一体优化的，实际飞行任务中如果只需其中一个性能指标最优，就可设置其它性能指标的权系数为0。

1)由仿真结果可以得到详细的飞行时间窗口

飞行器从地球飞往火星时所选择的时间窗口与逃离速度，缩短了飞往火星的飞行时间;同时飞行器从火星返回地球时所选择的时间窗口与逃离速度，也缩短了返回地球的飞行时间，并使总的往返飞行时间最短，全部往返飞行时间为

图4 探测器出发后控制量随时间的变化

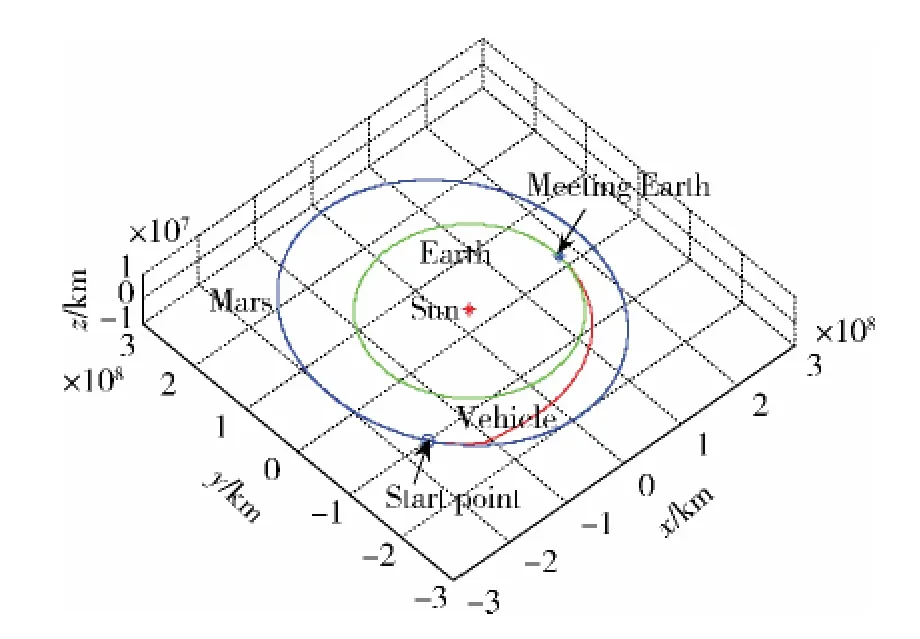
图5 探测器从火星到地球的最优飞行轨迹

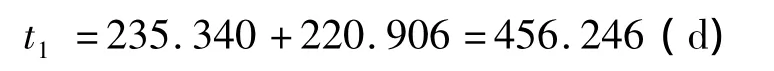
同时，以上时间窗口的选择满足了飞行器在火星上的探测时间，即飞行器在火星上探测时间为:

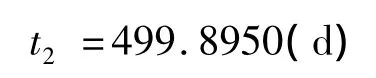
2)燃料消耗量也同时得到了最小化

从图4和图8可以看出，探测器在整个飞行任务中燃料消耗了850kg，包括地球飞往火星消耗的燃料和完成火星探测后返回地球飞行消耗的燃料。

3)满足各种约束条件

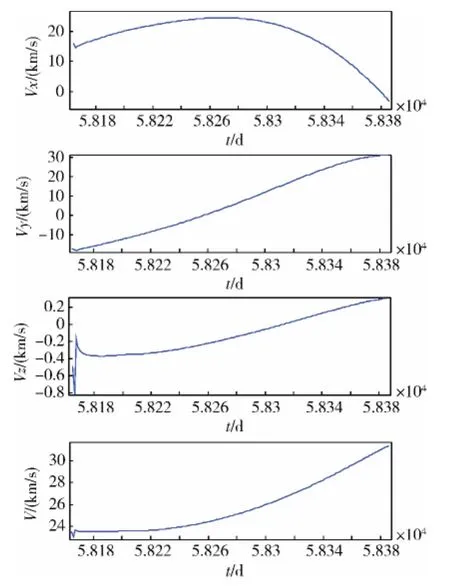
图6 探测器返回时速度随时间的变化

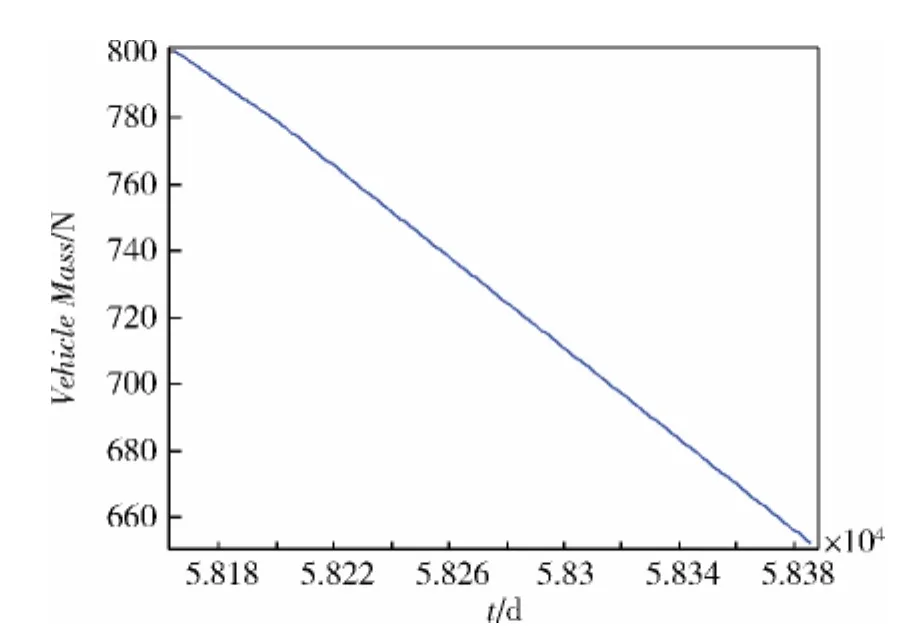
图7 探测器返回时质量随时间的变化

满足控制变量约束:从图4和图8可以看出，整个飞行任务过程中控制变量u小于0.2N。

满足飞行状态的终端约束:探测器从地球出发飞往火星，到达火星(离火星球心距离4485km)时飞行器相对火星的速度为ΔVM，f=2.5km/s，即满足ΔVM，f≤4.0km/s;探测器从火星返回地球，到达地球(离地心距离6491km)时飞行器相对地球的速度为 ΔVE，f=5.12km/s，即满足 ΔVE，f≤ 11.0km/s。

4)隐含了借力飞行

从图2与图6可以看到，在飞行器靠近火星或地球时，飞行速度大小在增大，距离目标星的相对距离在减小，这隐含了飞行器借力飞行。

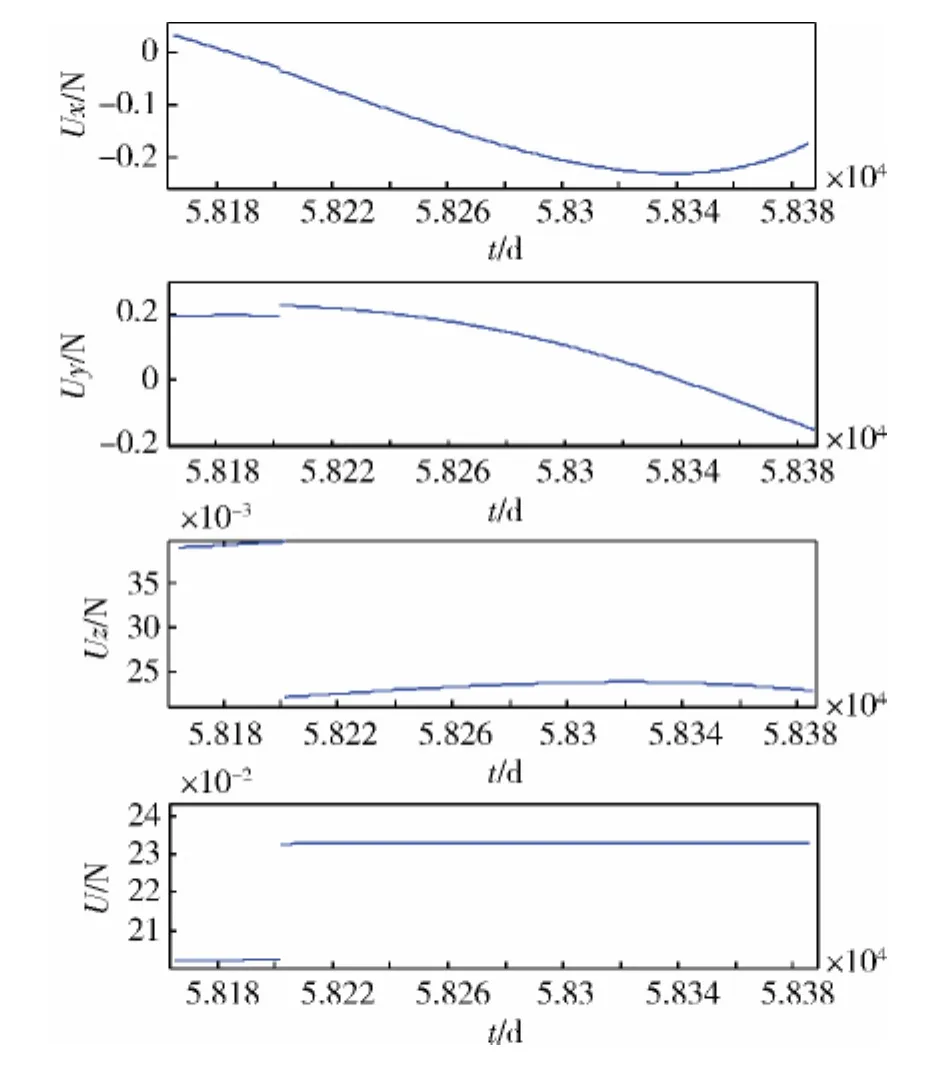
图8 探测器返回时控制量随时间的变化

4 结论

针对探测器在地球与火星之间往返飞行轨迹的全局一体化优化设计问题，采用一种航天器轨迹优化的组合算法，即静态参数优化+动态优化相互迭代的数值优化算法。在满足全部各种约束条件下，经过大规模的数值飞行仿真，得到了在地球与火星之间的全局一体的最优往返飞行轨迹，其中包括探测器分别离开地球与火星时的最优发射时间窗口与逃逸速度等。该飞行器沿着最优4-D轨迹飞行，可获得最小的燃料消耗量，最短的往返飞行时间(即有限时间内在火星上探测时间最长);另外，飞行器在达到火星或地球时，分别达到行星的相对速度均满足约束条件。这里指出，本文是基于多体动力学模型进行的轨迹优化，即隐含了借力飞行等因素，该飞行仿真结果具有实际的理论与工程价值，对未来我国火星探测飞行任务具有参考价值。

［1］ 张旭辉，刘竹生.火星探测无动力借力飞行轨道研究［J］.宇航学报，2008，26(9):1739-1746.(ZHANG Xuhui，LIU Zhusheng.Unpowered Swing by Flight Orbit Design for Mars Exploration ［J］.Journals of Astronautics，2008，26(9):1739-1746.)

［2］ Takeshi Tsuchiya，Takashige Mori.Optimal design of two-stage-to-orbit space planes with airbreathing engines［J］.AIAA，2005，42(1):90-97.

［3］ 尚海滨，崔祜涛，崔平远，栾恩杰.地球到火星的燃料最省小推力转移轨道［C］.中国宇航学会深空探测技术专业委员会第一届学术会议，2005.1.

［4］ 尚海滨，崔平远，栾恩杰.地球-火星的燃料最省小推力转移轨道的设计与优化［J］.宇航学报，2006，27(6):1168-1173.(SHANG Haibin，CUI Pingyuan，LUAN Enjie.Design and Optimization of Earth-Mars Optimal-Fuel Low-Thrust Trajectory ［J］.Journals of Aeronautics，2006，27(6):1168-1173.)

［5］ 黄国强，南英，陆宇平.二级入轨空天飞机上升轨迹优化［J］.宇航学报，2010，31(3):641-647.(HUANG Guoqiang，NAN Ying，LU Yuping.The Ascent Trajectory Optimization of Two-stage-to-Orbit(TSTO)Space Plane［J］.Journal of Aeronautics，2010，31(3):641-647.)

［6］ Long Yaosong，Ye Zhengyin.Trajectory Global Optimization for Spacecraft Launched from the Earth in the Whole Solar System ［J］.Journal of Aeronautics，2012，33(2):160-166.

［7］ 黄国强，南英，陆宇平.小推力深空探测轨道全局优化设计［J］.航空学报，2010，31(7):1366-1372.(HUANG Guoqiang，NAN Ying，LU Yuping.Global Trajectory Optimization in Space Exploration by Lowthrust［J］.Acta Aeronautics et Astronautica Sinica.2010，31(7):1366-1372.)

［8］ 胡海龙，南英.有翼火星探测器进入轨迹优化设计［C］.第一届进入减速与着陆全国学术会议，2013，7.

［9］ 南英，陆宇平，龚平.登月返回地球再入轨迹的优化设计［J］.宇航学报，2009，30(5):1842-1847.(NAN Ying，LU Yuping，GONG Ping.Optimal reentry trajectory design for mooncraft returning to the earth ［J］.Journal of Aeronautics，2009，30(5):1842-1847.)

［10］ 南英，陈士橹，严辉.航天器轨迹优化的通用数值算法［J］.飞行力学，1996，14(3):20-25.(NAN Ying，CHEN Shilu，YAN Hui.A common numerical calculation method of optimizing the trajectories of space vehicles［J］.Flying Dynamics，1996，14(3):20-25.)

［11］ Huang Guoqiang，Lu Yuping，NanYing.A survey of numerical algorithms for trajectory optimization of flight vehicles［J］.Science in China Series E，2012，55(9):2538-2560.

［12］ NAN Ying，Hang Guoqiang，Lu Yuping，Gong Ping.Global 4-D Trajectory Optimization for Spacecraft［J］.Science China，2010，53(8):2097-2101.

［13］ 李鑫，南英，黄国强，华鹏，吴胜亮.改进遗传算法的航空炸弹弹道反设计研究［J］.火力与指挥控制，2013，38(11):1960-1968.(LI Xin，NAN Ying，HUANG Guoqiang，HUA Peng，WU Shengliang.Reserve Design of Uncontrolled Bomb Trajectory Based on Improved Genetic Algorithm［J］.Fire Control＆ Command Control，2013，38(11):1960-1968.)

［14］ 南英，丁全心，陈哨东，黄国强，邹杰.基于自然数值算法的众多飞行器轨迹一体化全局优化设计［J］.中国科学，2013，43(6):636-659.(NAN Ying，DING Quanxin，CHEN Shaodong，HUANG Guoqiang，ZOU Jie.Global Optimal Design of Trajectories for Multiple Flight Vehicles Based on Natural Numerical Algorithm［J］.Science China，2013，43(6):636-659.)