自锚式悬索桥主缆分析与计算
张龙龙,钟 山
(江西省公路工程检测中心)
自锚式悬索桥主缆分析与计算
张龙龙,钟 山
(江西省公路工程检测中心)
自锚式悬索桥成桥时主缆线形与主缆无应力长度的精确分析计算是桥梁施工控制重要的一环,也是保证桥梁成桥后几何线性达到设计要求的必要条件。通过分别用分段悬链线法、抛物线法和有限元法计算一工程实例后,对比分析结果得出,有限元法和分段悬链线法(精确算法)的计算结果基本吻合,抛物线法的计算结果有一定的误差。这可为自锚式悬索桥的设计和研究提供参考。
自锚式悬索桥;主缆线形;分析;计算
0 引 言
自锚式悬索桥因其结构新颖,外形美观, 不需要体积庞大的锚碇,节省了锚碇昂贵的费用,降低了其造价成本,加上跨越能力很大,能满足跨江及通航的要求,对地质地形的要求不高等显著优点,近年来备受工程界的青睐。
自锚式悬索桥兼有梁和索的受力特点,主缆是这种结构体系主要的承重构件,主缆锚固在加劲梁上,致使加劲梁受到很大的水平力,这相当于给了加劲梁一个预应力,有助于加劲梁承担恒载。主缆因几何形状的改变,影响体系平衡,表现出大位移非线性的力学特性,主缆在荷载作用下产生的变形会直接影响整个桥的受力分配,因此,自锚式悬索桥主缆的准确的分析和精确的计算对桥梁施工控制是至关重要的。用分段悬链线法、抛物线法和有限元方法分别对一工程实例进行主缆线形计算,对结果进行对比分析。
1 自锚式悬索桥主缆计算原则及计算方法
1.1 计算原则
自锚式悬索桥在各阶段计算的时候,必须遵守一个原则就是构件质量守恒和无应力尺寸不变的原理。即:在施工的任何阶段构件的自重恒载必须保持一致,在施工的任何阶段构件的无应力尺寸需等于成桥阶段时的无应力尺寸。因此,自锚式悬索桥成桥时主缆线形与主缆无应力长度的准确分析计算是桥梁施工控制重要的一环,也是保证桥梁成桥后几何线性达到设计要求必须满足的条件。
1.2 计算方法
自锚式悬索桥主缆线性计算的方法主要是抛物线法、分段悬链线法及有限元计算法。
(1)抛物线法和分段悬链线法
抛物线法和分段悬链线法都是基于假定单独进行主缆分析,通过迭代计算主梁在给定荷载下的平衡状态。抛物线法计算有应力长度时,是用集数展开式的有限项积分求得,是又一次的近似,和分段悬链线法对比容易看出分段悬链线法计算该方面要精确的多;两种方法都是用完全积分的方法计算弹性伸长的,计算这一项两种方法的差别很小。抛物线法和分段悬链线法具体的介绍从略。
(2)有限元计算法
自锚式悬索桥主缆成桥线形和主缆无应力长度的精确分析是保证结构成桥后几何线形达到设计要求的必要条件,也是施工控制的关键一步。悬索桥的缆索体系具有显著的几何非线性,相比其他桥型,悬索桥在施工阶段可以算是最柔的结构,在对悬索桥进行分析计算时必须要有很高的精度才能满足施工要求,因为整个施工阶段桥梁会发生很大的刚体位移、吊装的梁段要临时连接、鞍座要预偏和顶推,因此对于悬索桥的分析计算就需要采用非线性功能较强的有限元分析软件。
通用的空间有限元分析软件—Midas civil具有较强非线性分析功能。Midas civil软件通过两个步骤计算自锚式悬索桥的精确线形。第一步使用“节线法”粗略的确定了主缆线形和坐标,这一步的平衡条件只考虑了加劲梁的自重。第二步采用悬链线单元,用“节线法”求得的主缆线形和无应力索长作为基础,以主缆与加劲梁的重量作为平衡条件再次进行迭代分析,并生成地锚式悬索桥模型。
“悬索桥建模助手”计算的主缆线形和无应力索长等结果,对于地锚式悬索桥可以用其进行其他分析内容。但对于自锚式悬索桥,桥梁的整个主缆体系发生了变化,需要由“悬索桥建模助手”生成的模型根据实际桥型进行相应的修改,再使用“悬索桥分析控制”功能,进行第二步精确迭代分析,计算出最终的主缆线形和无应力索长。
2 工程概况及模型建立
2.1 工程概况
某自锚式悬索桥跨径布置为70 m+160 m+70 m,大桥全长508.32 m,主桥为跨径300 m的钢筋混凝土自锚式悬索桥,两塔高均为34.20 m,中跨吊杆间距20×8 m,边跨吊杆间距7×8 m+14 m。设计荷载为城市—A级,人群荷载4.0 kN/m2,加劲梁采用钢筋混凝土单箱五室箱梁,梁顶板宽25 m,梁高2.5 m。顶板厚度20 cm,底板厚度18 cm,边腹板厚45 cm,中间腹板厚35 cm。主梁因主缆水平分力的作用,主梁按全预应力混凝土结构考虑。
中跨矢跨比为1/6,主缆截面直径54.3 cm,由85根Φ54 mm镀锌钢丝绳组成,钢丝标准强度为1 960 MPa。吊杆采用121×Φ7.1 mm镀锌高强平行钢丝,强度为1 670 MPa,桥梁结构尺寸图如图1所示。

图1 桥梁结构尺寸图(单位:m)
2.2 模型建立
秉着全桥组合有限元的分析思想,应用Midas civil有限元软件建立全桥计算模型,模型的建立应着重模拟结构的质量、刚度和边界条件,使它们尽量和实际结构相符。根据结构计算需要和本桥结构特性,将桥梁结构离散成平面梁、索单元计算。塔和梁离散成平面梁单元,主缆和吊杆离散成平面索单元。全桥模型如图所示,模型包含138个索单元,140个梁单元,277个节点,有限元计算模型如图2所示。

图2 有限元计算模型
3 计算结果对比分析
按照以上所述的三种方法分别对该桥进行计算,列出成桥恒载状态和空缆状态下的主缆坐标、主缆内力、索长以及索鞍预偏量计算结果进行对比分析。
3.1 主缆坐标
分段悬链线法、抛物线法及Midas civil软件算法计算的自锚式悬索桥在成桥恒载和空缆两种状态下的主缆坐标计算结果如表1、表2和表3所示。
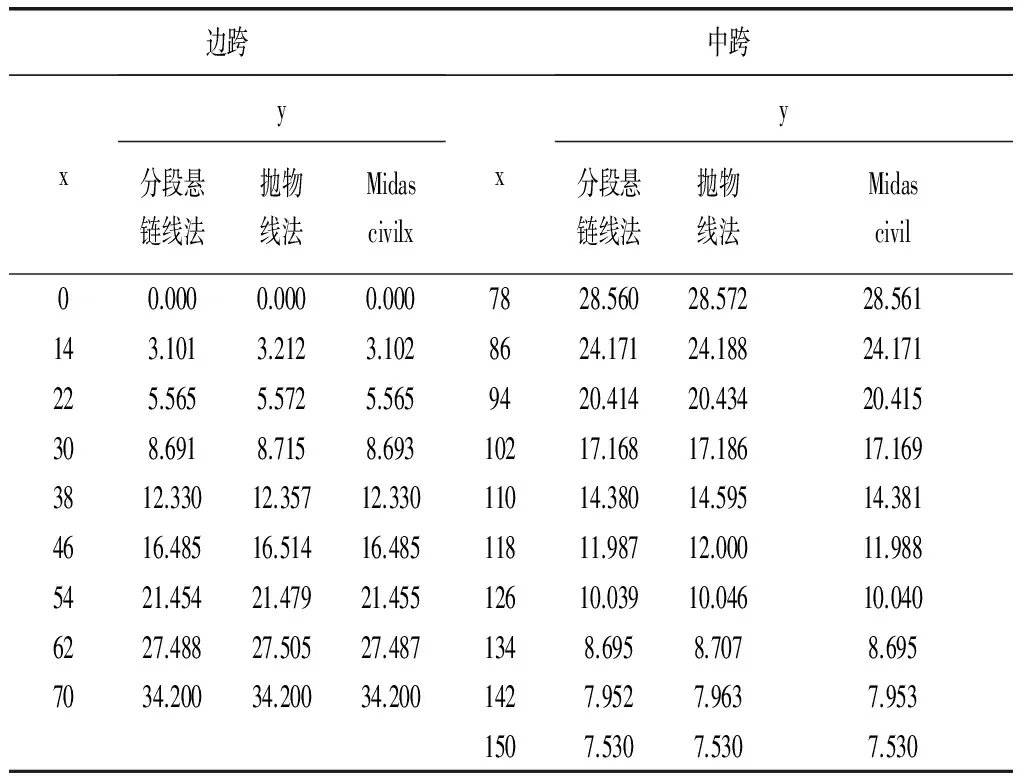
表1 成桥恒载状态的主缆坐标 m

表2 空缆状态的边跨主缆坐标 m

表3 空缆状态的中跨主缆坐标 m
3.2 主缆内力、索长和索鞍预偏量
成桥恒载状态和空缆状态下的主缆内力、索长以及索鞍预偏量计算结果如表4和表5所示。

表4 成桥恒载状态的内力和索长

表5 空缆状态的内力、索鞍预偏量和索长
从计算结果可以看出,相对于采用分段悬链法假定的精确方法,近似的抛物线法在自锚式悬索桥主缆线形计算时具有计算简便的优点,但会带来一定程度的误差。对于成桥恒载状态,抛物线法计算的误差很小,一般可以满足工程设计和施工的精度要求,但空缆状态的吊点坐标和索鞍预偏梁结果误差很大,须予以重视。Midas civil 软件通过两个步骤计算的自锚式悬索桥精确线形与分段悬链线法计算结果基本吻合。
4 结 语
自锚式悬索桥主缆在架设完成后,线形基本不能再做调整,如果需要调整,也只能微调,因此其主缆线形的精确计算显得更为重要。通过对比三种计算方法的计算结果,抛物线法的计算结果有一定的误差,分段悬链线法(精确算法)和有限元法计算结果基本吻合,这也说明有限元法的精度很高,完全能满足设计要求。
[1] 张哲.混凝土自锚式悬索桥[M].北京:人民交通出版社,2005.
[2] 沈锐利.悬索桥主缆系统设计及架设计算方法研究[J].土木工程学报,1996,29(2):3-9.
[3] 周孟波.悬索桥手册[M].北京:人民交通出版社,2003.
[4] 谭冬莲.大跨径自锚式悬索桥合理成桥阶段的确定方法[J].中国公路学报,2005,(4).
[5] 李建慧,李爱群,袁辉辉,等.独柱塔空间缆索自锚式悬索桥缆索线形计算方法[J].公路交通科技,2009,26(10):66-70,75.
2015-03-16
张龙龙(1987-),男,江西南昌人,助理工程师,研究方向:桥梁检测与加固。
U442
C
1008-3383(2015)12-0080-02

