光纤陀螺加速退化试验方法研究

袁慧铮，陈林华，陆俊清，李星善

(1.湖北航天技术研究院总体设计所，武汉 430040；2.第二炮兵驻8602厂军事代表室，湖北 孝感 432000)



光纤陀螺加速退化试验方法研究

袁慧铮1，陈林华2，陆俊清1，李星善1

(1.湖北航天技术研究院总体设计所，武汉 430040；2.第二炮兵驻8602厂军事代表室，湖北 孝感 432000)

光纤陀螺作为日渐成熟、广泛应用的全固态、高可靠性惯性器件，其性能退化的规律已经成为当前各应用系统关注的热点。加速退化试验技术是解决高可靠长寿命产品的性能评估等工程领域问题的一种常用方法，可以在较短时间内对产品的寿命特征进行预测。从光纤陀螺自身的特点出发，选择标度因数稳定性和零偏稳定性作为衡量光纤陀螺性能保持期的主要指标。根据使用环境的具体要求，采用温度作为其加速应力，并对退化试验方法、数据处理方式以及加速方法的合理性进行了分析和论证。

光纤陀螺；加速；退化；温度

0 引言

光纤陀螺(FOG)具有全固态、体积小、重量轻、启动快、可靠性高等优点，已经逐步取代三浮陀螺、挠性陀螺，在各型武器装备上得到了广泛的应用。大多数应用环境对光纤陀螺的要求为“长期贮存、一次使用”，需要保证其在长期贮存后依然保持良好的战技性能。为保证其良好的使用性能，对其主要性能参数需要每隔一定时间进行重新标定测试，而这个标定测试间隔又称为性能保持期。一般认为，作为一种长寿命的惯性器件，其性能退化是非常缓慢的。因此，可近似认为光纤陀螺的每个性能保持期的时间跨度是相同的。性能保持期既关系到武器装备能否达到随时可用和能用的要求，又关系到不合理的标定、返修周期所造成的经济损失。因此，如何采用加速退化的试验方法在工程允许的时间内获得足够的性能退化数据，对其性能退化规律进行预测，进而确定光纤陀螺的性能保持期，是一个亟待解决的课题。

国外对加速退化试验的研究始于20世纪80年代，近30年来，Nelson、Meeker、Escobar等对加速退化试验技术的理论和方法进行了深入的研究。20世纪90年代初，加速退化试验逐渐引起国内统计学界和可靠性工程学界的广泛关注。加速退化试验是在失效机理不变的条件下，通过提高应力水平来加速产品性能退化，利用高应力水平下的性能退化数据来估计产品在正常使用应力下的可靠性特征。因此，加速应力水平选择的基本原则为，最高应力应接近或等于该产品技术标准中规定的额定值，但不得大于该产品结构材料、制造工艺所能承受的极限应力，以免带来新的失效机理。当前对于光学及光电组件的寿命测试可参考的工业标准是Telcordia公司制定的GR-468-CORE和GR-1221-CORE系列标准[1-2]，这些标准建议，无源器件应该在温度85℃、相对湿度85%的环境中测试500h，良好密封的有源器件应该在85℃的环境中测试2000h。当不能通过测量得到实际任务时间时，可以设计加速试验进行产品寿命估计。

1 加速应力和测试参数选择

通常情况下，影响光纤陀螺性能的环境因素有温度、湿度、大气压力、降水、宇宙辐射、沙尘、霉菌、盐雾、机械因素、大气污染等，本文主要研究光纤陀螺的库房贮存情形，考虑到光纤陀螺的贮存环境条件、产品防护包装以及产品贮存期间的检测与维修情况，光纤陀螺主要会受到温度、湿度和冲击等环境因素的影响。

贮存过程中，温度应力来源于环境温度的变化，主要会加速产品退化、失效的化学反应和物理变化过程；湿度应力来源于环境中的水汽，特别是气候潮湿地区湿度应力的影响更加明显，主要会引起并加速金属件的电化腐蚀和化学腐蚀，非金属的水解、霉变和热分解；冲击来源于倒库或运输时的振动和跌落、碰撞，主要会引起产品的永久性变形、产品表面产生裂纹以及光纤断裂等。

由于光纤陀螺在工艺上一般采用整体密封、减震安装的方式进行使用，且贮存过程中一般不会拆卸或运输，因此可忽略湿度和冲击因素。在加速应力的选择上，主要考虑昼夜、四季变化温差对光纤陀螺性能的影响。进行温度应力加速试验的方式有很多种，如采用温度循环的方式模拟温度的昼夜、四季变化，或采用步进应力的方式，间隔一定时间后逐步提高试验温度，直到产品性能劣化程度超出正常使用的范围。但从数据处理及结果准确度的角度来考虑，前者数据处理方式复杂，后者易引入自然老化条件下不存在的失效模式，从而影响产品性能保持期的预测。因此，本文采用了应用最成熟、最广泛的加速试验方法，即在恒定温度应力的条件下进行光纤陀螺的加速退化试验，以兼顾试验效率和试验准确度。

光纤陀螺的主要性能参数有零偏值、零偏稳定性、标度因数稳定性、标度因数非线性、死区、失准角等参数，其中标度因数稳定性和零偏稳定性为光纤陀螺的两个主要应用参数，表征了包括光学器件、电子元器件以及结构件整体性能退化的趋势。因此，本文选择光纤陀螺的标度因数稳定性和零偏稳定性作为其性能退化的特征参量。需要指出的是，由于光纤陀螺的参数可以通过重新标定来修正，因此，本文考虑的主要是光纤陀螺在某个性能保持期中的参数退化情况。

2 加速退化试验的数学模型

2.1 寿命分布函数

在可靠性工程中，常见的概率分布有指数分布、正态分布和威布尔分布。其中，威布尔分布在分析半导体、电子元器件以及机械器件的失效分布方面得到了广泛的应用。实践证明，凡是由于某一局部失效或故障引起全局机能失效的元件、器件、设备或系统等的寿命都服从威布尔分布[3-4]。威布尔分布的特点是兼容性好，对各类数据的拟合能力强，可以全面的描述产品不同失效期的失效过程与特征，指数分布、正态分布都可看作是威布尔分布的特例。双参数的威布尔分布有效地分析了初期致命失效，实用寿命的和耗损阶段的寿命数据，也可用于失效率的增长、持续和递减。考虑到光纤陀螺的特点，设光纤陀螺的性能退化服从位置参数γ=0的威布尔分布，其累积密度函数为

F(t)=1-e-(t/η)β，t>0

(1)

式中，β为斜率(形状参数)，η为特征寿命(尺度参数)。累积密度函数给出了时间t内的失效概率。参数η和β由失效时间进行估计，如果失效数据服从威布尔分布，η和β的值代入累积密度函数的公式，即可求出一定时间内元器件的失效情况。

2.2 加速模型

加速退化的基本思想是利用高应力下的寿命特征去外推正常应力水平下的寿命特征。实现这个基本思想的关键在于建立寿命特征与应力水平之间的关系，利用这个关系实现外推正常应力水平下寿命特征的目的。这种寿命特征与应力水平之间的关系就是通常所说的加速退化模型[3]。

加速退化模型可以分为以下三种基本类型：

1)物理加速模型。物理加速模型是通过与失效机理相关的物理原理推导得到的加速模型。例如，表征温度应力与产品性能的Arrhenius模型，表征温度应力与产品性能的单应力艾林模型，表征机械应力或者电应力与产品性能的逆幂律模型，表征温度应力和另外一种应力共同作用与产品性能的广义艾林模型。

2)基于统计数据的加速模型即数学加速模型。基于统计数据的加速模型是用统计模型来描述加速退化数据的。

3)经验加速模型。由试验室大量试验总结经验获取的加速模型。

光纤陀螺是典型的光、机、电一体化精密仪表，包括光源、耦合器、探测器、光纤环、数字处理电路以及安装结构等，且安装结构中存在非金属结构件与金属构件混装的情形，设计复杂，性能退化机理不明显。但光纤陀螺所用的有源器件，如光源等，基于半导体工艺，有相当多的研究资料证实其性能退化满足一定的物理规律；而光纤耦合器、光电探测器、光纤以及绕环胶水等部件和成分，均会随着时间而逐渐老化，且这种老化可以从物理或化学的角度进行合理的解释。因此，选择物理加速模型作为光纤陀螺的加速退化模型。

常用的物理加速模型主要有Arrhenius模型、逆幂律模型和艾林模型。其中Arrhenius模型和逆幂律模型主要描述单应力条件下待评估对象的性能退化规律，艾林模型分单应力艾林模型和广义艾林模型，后者适用于多种应力共同作用下的待评估对象加速退化。由于本文主要考虑温度对光纤陀螺性能的影响，且光纤陀螺的主要光学部件，如光源、Y波导和光纤环等，均满足Arrhenius加速规律。因此，选择Arrhenius模型作为光纤陀螺的温度应力加速退化模型[5-6]，具体表达式为

(2)

式中，M为光纤陀螺的性能退化量； ∂M/∂t为温度为T(绝对温度)时的退化速率，退化速率是时间t的线性函数；k为波尔兹曼常数，为8.617×10-5eV/℃；T为绝对温度；A0为常数；t为反应时间；ΔE为失效机理激活能，以eV为单位，同一类产品的同一种失效模式为常数。

3 试验数据分析方法

3.1 原始试验数据处理

采用Arrhenius模型进行原始数据处理，则至少要有两个不同温度点的试验数据，才能求解出模型中的相关参数。假设试验设定了温度T1、T2、T3、T4共四个不同的温度应力，并分别抽取样本进行试验，每组试验取N+1个等间隔测试点，记陀螺性能退化量为Bij，式中i=1～4，代表试验的温度点；j=1，2，…，N，代表性能退化量的测量点。对式(1)进行移项并取对数，可得

(3)

y=βx-βlnη

(4)

通过最小二乘法进行线性拟合，进而得到β和η的值。

3.2 计算激活能

如果原始试验数据满足威布尔分布，则Arrhenius模型与威布尔分布存在如下的关系[5]

(5)

式中，b为截距。通过最小二乘法进行线性拟合，即可得到光纤陀螺性能退化的激活能ΔE。

3.3 计算加速因子

对于加速退化试验而言，最为关键的是要找到加速条件与正常条件之间的加速因子。对于满足威布尔分布的光纤陀螺性能退化量而言，采用Arrhenius退化模型，则其加速因子为

(6)

式中，AF为加速因子，k为波尔兹曼常数，T1和T2分别为正常条件与加速条件的温度值。设 为光纤陀螺在正常条件下性能保持期，为光纤陀螺在对应加速退化温度点处的性能保持期，两者之间存在如下关系

ηu=AF×ηs

βu=βs

(7)

3.4 估算光纤陀螺的性能保持期

按照实际需求设定置信区间，根据已经得到的ηu和βu值，代入式(1)，即可得到光纤陀螺的性能保持期。

4 产品数据及试验结果分析

4.1 产品数据统计分析

从已交付的产品中随机抽取45只进行测试数据统计，设定合理的超差阈值，在本文中，超差阈值设定为性能下降10%，定义产品指标超差的术语为产品失效。采用线性直插的方式，得到产品的性能保持期如表1所示。从表1中可知，产品性能保持期离散度很大。经分析，存在两方面的原因，一方面是产品在生产过程中，由于工艺水平的限制，有的性能指标特别稳定，基本保持不变，而有些产品性能指标相对不稳定，波动较大；另一方面是，表中数据是采用线性插值的方式得到的，插值算法本身的合理性也会造成数据离散度增大。

表1 产品性能保持期统计Tab.1 Statistics of product performance retention period

利用式(1)表述的模型，对表1中所列数据进行建模分析，得到产品的失效概率分布图，如图1所示。

图1 产品标度因数与零偏随时间自然老化失效概率分布Fig.1 The failure probability distribution of scale factor and bias VS.time under natural aging

从图1中可以看出，该模型能满足大部分数据的拟合要求。经计算，标度因数稳定性和零偏稳定性的β值分别为1.16和1.43。产品随着时间的增长，其可靠度逐渐下降，如图2所示。

图2 产品标度因数与零偏随时间自然老化可靠度变化情况Fig.2 The reliability distribution of scale factor and bias VS.time under natural aging

对于产品性能保持期的估计，参考GR-1221-CORE中关于可靠性的建议，将产品性能参数退化10%的情形定义为产品性能保持期，得到标度因数的性能保持期为48.37月，零偏的性能保持期为69.10月。考虑到产品的实际应用情况，则可认为该型光纤陀螺在自然贮存条件下的性能保持期不短于69个月。

4.2 加速退化试验数据分析

由于样本数量有限，因此，加速退化试验验证只能够设定一个高温加速应力。在本文中，随机选取了6只光纤陀螺进行高温60℃的加速退化试验，得到试验数据如表2和表3所示，标度因数变化量的单位为10-6，零偏变化量的单位为(°)/h。

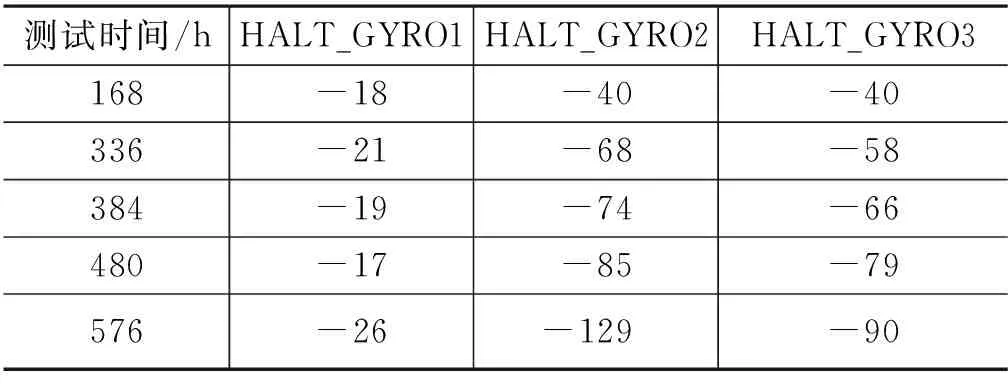
表2 加速退化标度因数试验数据Tab.2 Experimental data of scale factor under accelerated degradation

续表测试时间/hHALT_GYRO1HALT_GYRO2HALT_GYRO3648-24-134-92696-29-154-102测试时间/hHALT_GYRO4HALT_GYRO5HALT_GYRO6168-68-34-87336-109-62-159384-131-76-190480-149-90-227576-174-108-273648-187-116-299696-203-133-317

表3 加速退化零偏试验数据Tab.3 Experimental data of bias under accelerated degradation

考虑到测试中的误差，对加速退化试验数据进行拟合后插值，根据式(1)～式(7)计算加速系数、激活能和失效率为10%时的性能保持期。

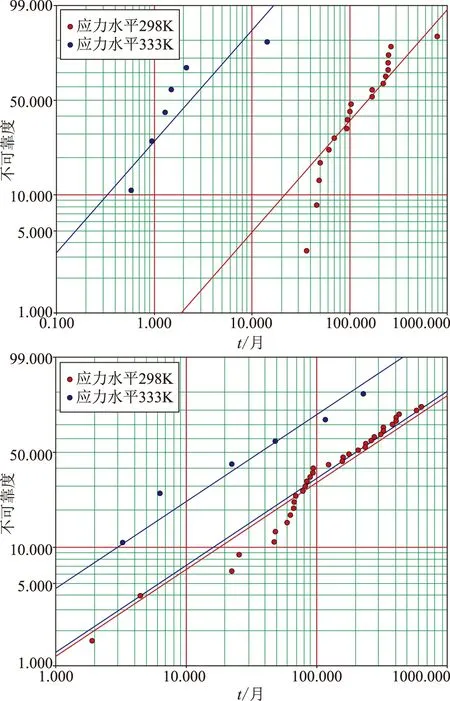
图3 产品标度因数与零偏在加速退化条件下的概率分布情况Fig.3 The failure probability distribution of scalefactor and bias VS.time under accelerated degradation

图3的上图和下图分别为标度因数稳定性和零偏稳定性的加速退化试验情况。由图3中可知，在加速条件下，产品的标度因数和零偏均有不同程度的加速退化。尤其是产品的标度因数稳定性，在加速条件下退化的更为迅速。经计算，标度因数稳定性和零偏稳定性的β值分别为1.02和1.17。从理论上说，如式(7)所示，加速退化情况下计算出的β值应与自然老化时的β值保持一致。但由于数据误差、样本数量的影响，两者的计算结果必然会存在一定的误差。从上述计算数据来看，该误差满足实际使用的需求。

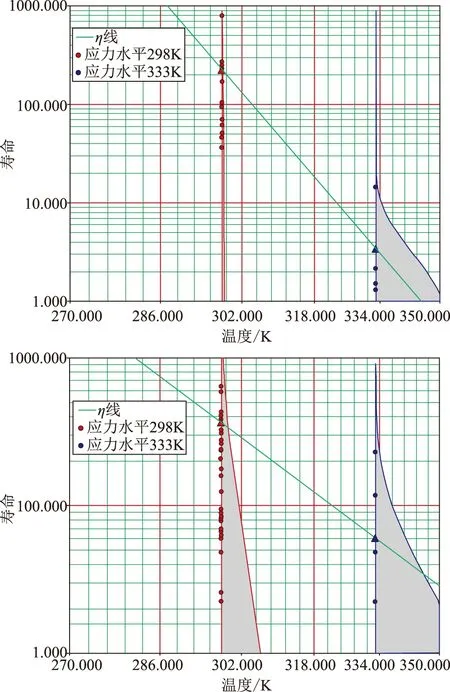
图4 产品性能保持期与应力之间的关系Fig.4 The relationship between product life and stress level

为考核不同温度应力下产品性能的退化规律，图4中绘出了产品性能保持期随应力的变化关系，需要特别指出的是，由于光纤陀螺的特殊性，其性能保持期包括标度因数稳定性和零偏稳定性两个方面。

根据产品加速退化的试验数据，计算出标度因数的性能保持期为36.68月，零偏稳定性的性能保持期为52.08月，加速系数分别为12.68和6.03，激活能分别为0.623eV和0.439eV，与GR-468-CORE和GR-1221-CORE中给出的参考值相近。该数据相比于自然老化数据的计算结果更为严格。因此，该加速退化试验方法具有参考意义，可用于同类产品性能保持期的评估。

5 结论

本文从光纤陀螺自身的特点出发，为预测其性能保持期，根据贮存环境的具体要求，选择了温度作为光纤陀螺的加速应力，并对加速退化试验方法、数据处理方式进行了分析和论证。通过对自然老化数据和加速退化数据的分析，得到了加速退化试验评估结果与自然老化数据分析结果相近的结论。

从更严谨的角度来说，进行加速退化试验，需要对数据进行一致性检验，确定试验的截尾时间等工作，进一步的，影响光纤陀螺性能退化的因素也可以适当扩展，并根据需求选择更合适的加速退化模型。

[1] GR-468-CORE，“Generic Reliability Assurance Requirements for optoelectronic Devices Used in Telecommunications Equipment”.Issue 2，2004.9.

[2] GR-1221-CORE，“Generic Reliability Assurance Requirements for Passive Optical Components”.Issue 2，1999.1.

[3] Weibull W.A statistical function of wide a pplicability[J].J.Appl.Mechanics，1951，18(3)： 293-298..

[4] 赵建印，孙权，彭宝华，周经纶.基于加速退化试验数据的可靠性分析[J].可靠性分析与研究，2005，7.

[5] 刘娟.电连接器步进应力加速退化试验技术的研究[J].中国知网，杭州，2013，3.

[6] 林震，姜同敏，程永生，胡斌.阿伦尼斯模型研究[J].可靠性与环境适应性理论研究，2005，6：12-44.

Research on Accelerated Degradation Method for Fiber Optic Gyro

YUAN Hui-zheng1，CHEN Lin-hua2，LU Jun-qing1，LI Xing-shan1

(1.The 9th Designing of China Aerospace Science Industry Crop，Wuhan 430040，China；2.Military Representative Office of the Second Artillery Force in 8602 Factory，Hubei Xiaogan 432000，China)

Fiber optic gyros(FOG)are all-solid inertial sensors with high reliability.With its widely application，FOG’s performance degradation rule has become the focus of attention.Accelerated degradation method is an widely-used method to estimate the life of products with reliability and long life.The method could predict the life of the product based on the available sample data in a shorter time.The scale factor and bias stability of FOG are chosen as the performance parameters.According to the specific requirements of the operating environment，temperature is taken as the acceleration stress.The degradation method，data processing method and the rationality of the accelerated method are discussed and demonstrated.

Fiber optic gyro； Acceleration； Degradation； Temperature

2015 - 03 - 28；

2015 - 05 - 16。

袁慧铮(1986 - )，男，硕士，工程师，主要从事惯性技术方面的研究。

E-mail：huizhengyuan@163.com

U666.1

A

2095-8110(2015)05-0063-07