小直径铣刀高速铣削316L不锈钢的切削合力研究

阙燚彬

(1.广西大学机械工程学院，广西南宁 530004;2.柳州职业技术学院机电工程系，广西柳州 545006)

小直径铣刀高速铣削316L不锈钢的切削合力研究

阙燚彬1，2

(1.广西大学机械工程学院，广西南宁 530004;2.柳州职业技术学院机电工程系，广西柳州 545006)

通过多因素正交试验，应用SPSS软件建立不锈钢小直径铣刀高速铣削316L不锈钢的最大切削合力回归经验公式，同时对回归模型进行显著性验证。最终得到对铣削参数的优化选择有一定的参考价值的分析结果。

小直径铣刀;高速铣削;316L不锈钢;切削合力;经验公式

0 前言

316L不锈钢属难加工材料，其黏附性及熔着性强，铣削时冲击、振动较大，铣刀刀齿崩刃和磨损非常严重。当前，不锈钢的小直径高速加工技术，国内外学者鲜有研究，所以通过小直径铣刀高速铣削316L不锈钢外形轮廓正交实验得出小直径铣刀高速铣削316L不锈钢的最大切削合力回归经验公式，对优化不锈钢的铣削工艺参数、提高其加工效率、降低加工成本有重要意义。

1 实验条件及工件制备

1.1 实验加工设备

(1)机床。实验采用Fanuc a-t14iflb加工中心(主轴最高转速为24 000 r/min)，该加工中心的数控系统为Fanuc数控系统。

(2)刀具。实验采用刀具直径为2 mm，刀柄直径为4 mm的GUK品牌钛铝涂层钨钢硬质合金两刃平底铣刀，铣削方式采用顺铣。

(3)切削合力采集系统。切削合力的采集系统包括:大连YDX-III9702型压电式铣削测力仪、YE5850电荷放大器、数据采集卡、数据采集软件和计算机组成。YE5850电荷放大器如图1所示。YDXIII9702压电式铣削测力仪却能以其高刚度、高灵敏度、高固有频率能很好地满足静、动态测试的要求，可测出任意方向力的3个相互正交的分量 (Fx，Fy，Fz)。

图1 YE5850电荷放大器

测试系统在使用前要做好相应的调试工作，首先给测力仪和电荷放大器设置专门的地线，使整个测力系统有一个统一的地线;然后，对电荷放大器进行调试，合理选择电荷放大器的量程和挡位，以便提高测量精度和减小噪声。在数据采集软件方面，由于此次的实验是小刀径小切深的高速铣削，故实验所测得的数据保持在100 N以内，所选取的采样频率为10 kHz。

1.2 工件的制备

实验所提供的工件材料为316L不锈钢，尺寸规格为120 mm×75 mm×50 mm，测量现场如图2所示。

图2 测量现场

2 外形轮廓侧铣加工实验方案及数据处理方法

2.1 实验方案

为了建立不锈钢小直径铣刀高速铣削的切削合力模型，作者设计了正交试验。通过正交试验和回归分析法研究切削参数 (切削速度vc、进给速度vf、径向切深Ad、轴向切深Ap)对工件切削合力的影响效果，同时建立切削合力的经验公式。为了体现试验的实际工程意义，该试验结合实际生产中的切削参数并按照本试验条件的要求进行适当调整以建立更加准确的切削合力以及粗糙度回归模型。正交试验的安排采用四因素三水平共27组实验，实验参数如表1所示。

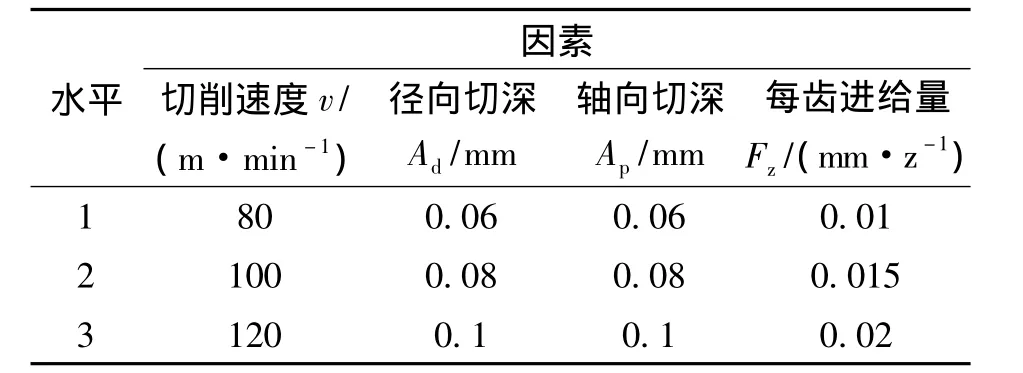
表1 侧铣正交试验参数表

2.2 数据处理方法

切削合力3个方向X、Y、Z的信号通过三向石英测力仪测得，进行切削实验时，每一组参数的实验进行3次切削，所以每一组参数的切削合力值取3次的平均值。

3 外形轮廓侧铣正交试验切削合力的实验结果

实验参数以及实验结果如表2所示。

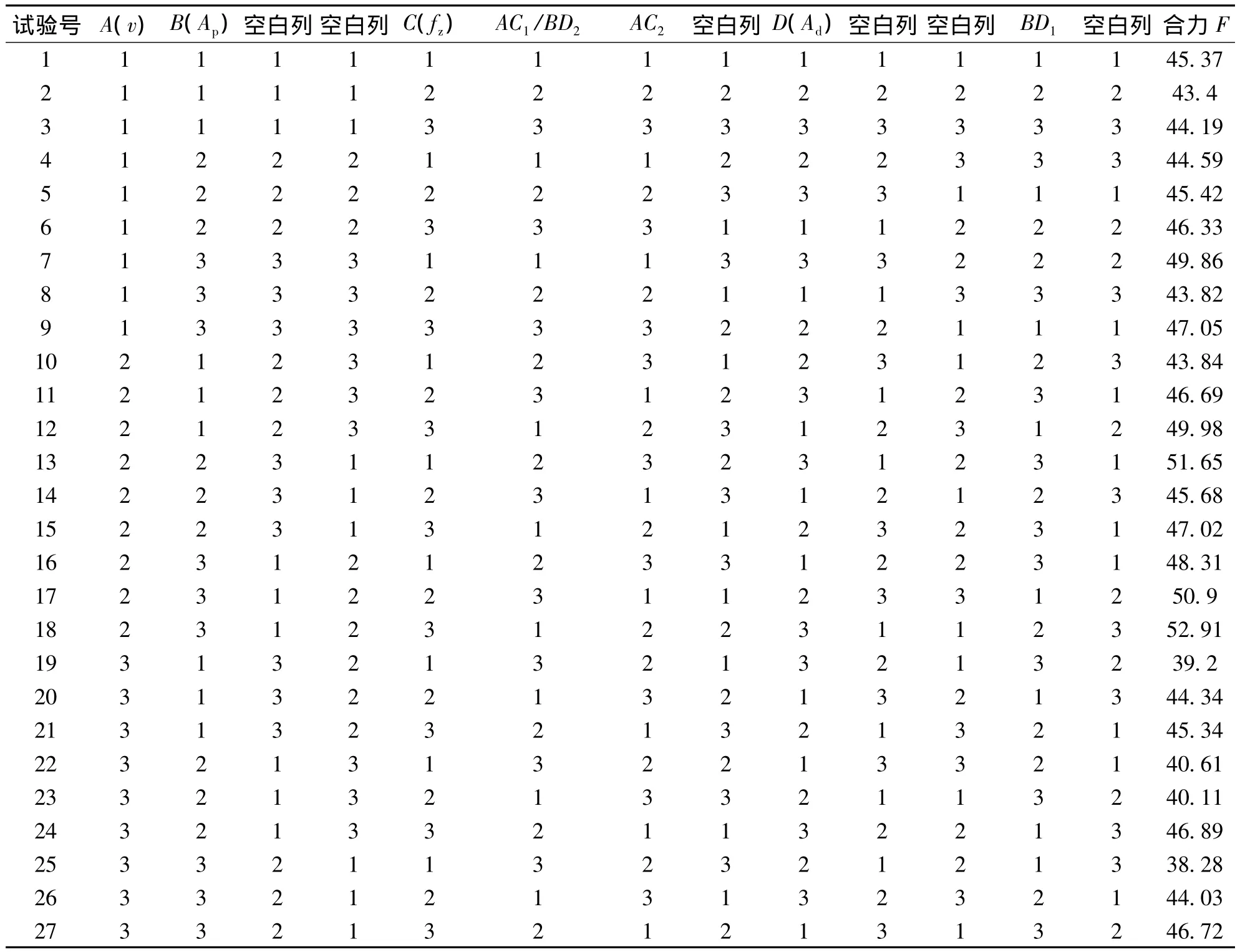
表2 侧铣L27(313)正交试验参数安排表及试验结果

4 外形轮廓侧铣切削合力回归模型经验公式的建立

回归模型常用来确定两个或两个以上变量对目标变量的定量关系，是一种常用的数理统计方法，广泛用于生产中的预测和控制。在实际问题的曲线类型不易判断时，可采用多项式进行逼近，因为，任意曲线都可以近似地用多项式来表示。如果变量y与x的关系可以假设为P次多项式，则多项式的模型为:

可以把上式的非线性项用不同的线性项来替代，则可以把上述问题用多元线性回归分析的方法来解决。即令

同理，多元多项式回归问题也可以化为多元线性回归问题来解决。

在上述问题中，由于事先对于切削合力与4个考察指标之间的回归曲线类型未知，所以采用多项式逼近，建立完全二次多项式模型:

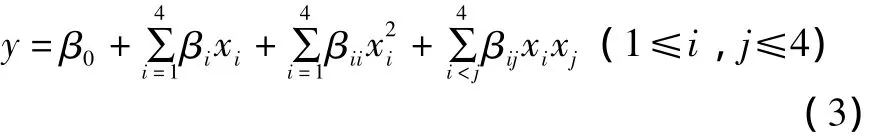
其中y表示切削合力，xi(i=1，2，3，4)分别表示切削速度、切削深度、进给量和切削宽度4个因素;系数βi表示xi的线性效应，βii表示xi的二次效应，βij表示xi与xj的交互作用效应。

利用SPSS软件，对试验数据进行统计分析。根据逐步回归分析结果，得到切削合力与4个因素的回归模型如下:

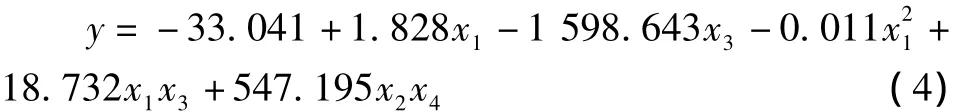
5 外形轮廓侧铣切削合力的回归模型的显著性检验

上节所建立的切削合力的回归模型 (4)只是一种经验概率模型，不能将试验中由于试验条件的改变引起的波动同实验误差引起的数据波动区分开来，对实际结果的拟合程度好坏有待进一步的检验，为此需要采用方差分析对该模型进行显著性检验。依据数理统计，方差分析的基本思想是将总的离差平方和QT分解为回归平方和QA和剩余平方和QE两部分来构造F统计量，并作F检验，进而判断各因素作用是否显著。

式中:r为试验选取因素的个数;n为试验组数，由正交试验表可知n=27、r=4。

则，由公式 (5)— (8)可得切削合力显著性检验表如表3所示。

表3 回归模型显著性检验表

模型的决定系数R2=0.748，说明y的74.8%可以由模型确定。

回归模型的F统计量 =12.456＞F0.01(5，21)=4.04，显著性检验的P值=0.000，远小于显著性水平0.01，说明所建立的切削合力的经验预测模型显著，能够较好地预测切削合力。

另一方面，对模型中各个变量的系数进行显著性检验，得到表4所示结果。

表4 回归模型系数显著性检验表

从表4可知，各个变量的显著性检验的P值均小于0.05，各个变量都显著。进一步说明了建立的模型的合理性。

运用经过显著性检验的切削合力回归模型，比较该模型的预测结果与实际试验结果误差如表5所示。

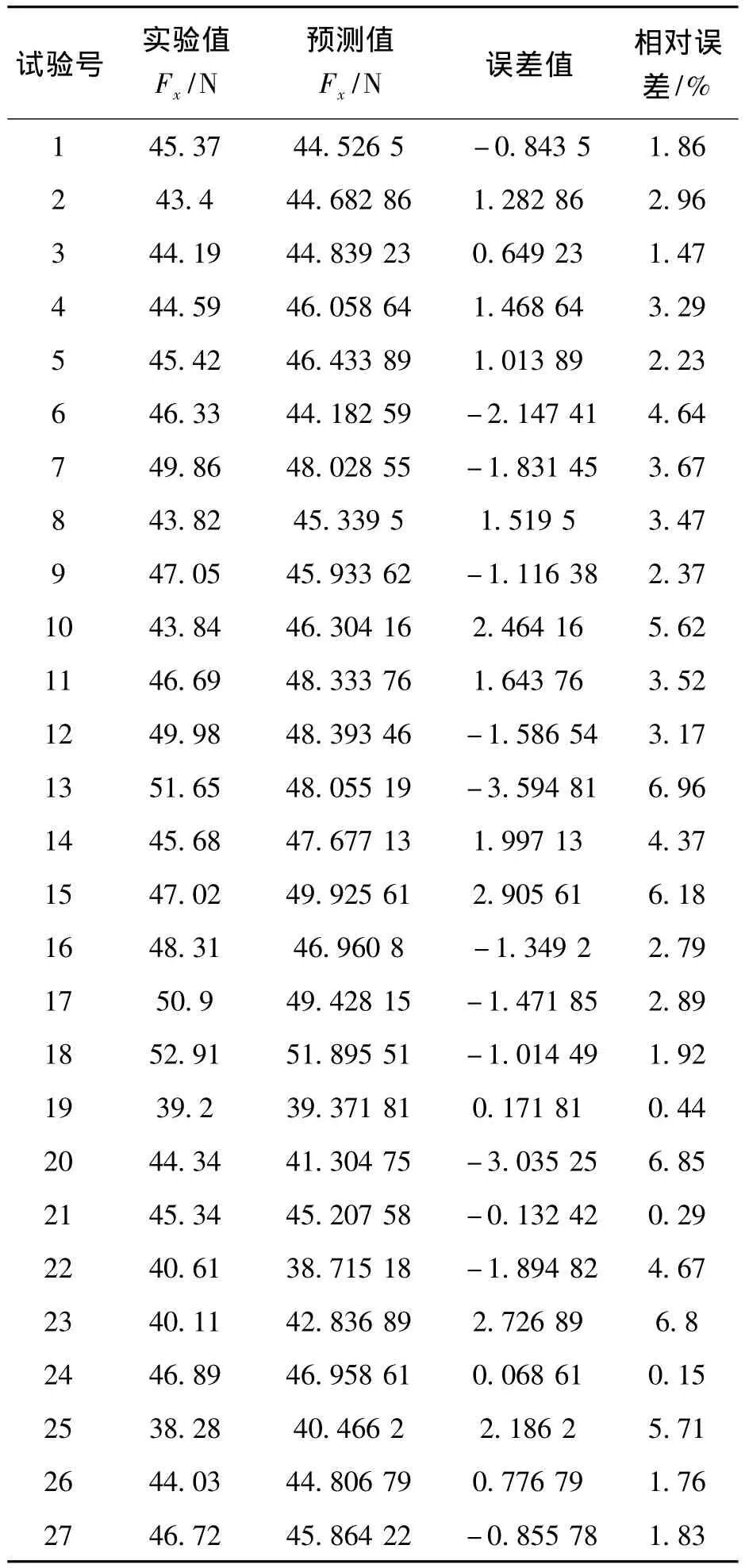
表5 预测模型误差分析表

从误差分析表可以看出，所有试验的预测误差均限制在10%之内，可见所建立的切削合力预测模型预测性能较稳定，可以用于侧铣切削合力的预测。

6 结束语

应用多因素正交试验法进行了小直径刀具高速铣削316L不锈钢外形轮廓的试验，建立了顺铣铣削316L不锈钢外形轮廓的小直径刀具铣削合力经验公式，并通过了显著性验证。应用该公式可以提前对所选定铣削参数的加工的铣削合力进行估算，对优化不锈钢的铣削工艺参数、提高其加工效率、降低加工成本有重要参考意义。

［1］曹雅莉.浅谈高速切削技术与发展［J］.轻工科技，2013(7):57－58.

［2］白琨.超高速切削加工及其关键技术［J］.新技术新工艺，2009(9):63－65.

［3］张伯霖，杨庆东，陈长年.高速切削技术及应用［J］.机电工程技术，2003，32(4):85 －86.

［4］张华伟.小直径铣刀高速铣削淬硬钢过程动力学仿真与有限元分析［D］.南宁:广西大学，2005.

Study of Cutting Force of Small Diameter Cutter with High Speed Milling of 316L Stainless Steel

QUE Yibin1，2
(1.College of Mechanical Engineering，Guangxi University，Nanning Guangxi530004，China;2.Department of Electromechanical Engineering，Liuzhou Vocational and Technical College，Liuzhou Guangxi545006，China)

Multi-factor orthogonalexperimentwas carried out.SPSSsoftwarewas applied to establish regression empirical formula for cutting force of small diameter stainless steel cutter with high speed milling of 316 l stainless steel，at the same time，the notable significance for the regressionmodelwas validated.Finally，the analysis of the results is obtained to have certain reference value to the optimization ofmilling parameters selection.

Small diametermilling cutter;High-speed milling;316L stainless steel;Cutting force;Empirical formula

TH16

A

1001－3881(2015)21－156－4

10.3969/j.issn.1001 －3881.2015.21.038

2014－09－17

阙燚彬 (1981—)，男，工程硕士，讲师，主要研究方向为先进制造技术。E－mail:queyibin@sina.com。