基于动力学补偿的并联机器人鲁棒轨迹跟踪控制研究

朱龙英，成磊，郑帅，陆宝发，赫建立

(1.盐城工学院汽车工程学院，江苏盐城 224051;2.常州大学机械工程学院，江苏常州 213164;3.安徽理工大学机械工程学院，安徽淮南 232001;4.江苏大学机械工程学院，江苏镇江 212013)

基于动力学补偿的并联机器人鲁棒轨迹跟踪控制研究

朱龙英1，成磊2，郑帅3，陆宝发4，赫建立2

(1.盐城工学院汽车工程学院，江苏盐城 224051;2.常州大学机械工程学院，江苏常州 213164;3.安徽理工大学机械工程学院，安徽淮南 232001;4.江苏大学机械工程学院，江苏镇江 212013)

针对6-DOF并联机器人系统存在动力学建模误差和外界不确定性因素干扰的问题，提出了一种基于动力学补偿的并联机器人鲁棒轨迹跟踪控制策略。在充分研究了机器人系统动力学模型特点的基础上，基于Lyapunov方法获得了并联机器人的鲁棒控制率，提出了一种鲁棒轨迹跟踪控制方法，采用逆动力学对内回路进行补偿，外回路采用PD控制，然后对并联机器人进行了鲁棒控制器的设计，最后通过MATLAB进行了系统的轨迹跟踪控制仿真分析。仿真结果表明:当系统存在外界周期干扰的状况时，系统轨迹跟踪误差仍然一致终值有界，在一定程度上提高了系统的鲁棒稳定性。

并联机器人控制;动力学补偿;Lyapunov方法;鲁棒跟踪控制

0 前言

并联机器人的优点包括结构简单、精度高、刚度大、承载能力强等，目前已被广泛应用于自动化领域［1］。但是它的缺点也很明显，从并联机器人的动力学观点来分析，其刚体动力学模型是一个高度非线性且具有强耦合性的复杂系统，传统的控制方法已无法对其轨迹跟踪精度进行很好的控制，因此，并联机器人系统的控制问题已成为目前急需解决的问题之一［2］。

PID控制器从出现发展至今，一直以其简单的构造和具有较好的鲁棒性而被广泛应用于解决复杂系统的控制问题，然而其控制参数是不变的，这就导致PID控制器的参数一般很难通过调节而获得最佳状态［3］。鲁棒控制被认为是提高并联机器人轨迹跟踪精度的一个较为有效的方法。文献 ［4］以3-RRR并联机构的轨迹跟踪控制为实际算例，使用了鲁棒控制器，通过分析得到了并联机器人即使存在模型误差的情形时，也能保证其轨迹跟踪误差能够始终迅速的变为零。并根据给定的轨迹运动参数结合MATLAB仿真验证了方法的合理性。文献 ［5－6］针对系统动力学模型的误差以及外界的干扰等因素对并联机器人动态响应性能的影响，利用Lyapunov方法对机构进行了鲁棒控制器的设计，最后结合MATLAB验证了该鲁棒控制器的稳定性，且可以减小运动时产生的轨迹跟踪误差，从而满足了对机器人轨迹跟踪精度的要求。赵东亚等［7］对一种6-DOF并联机构进行了非线性的分散鲁棒控制器的设计，运用Lyapunov方法对系统的稳定性进行了分析，并结合SimMechanics仿真验证了其有效性。KIM等［8］设计了一种带有摩擦估计器的鲁棒非线性控制器并将其应用于6-DOF并联机器人中，通过Alpha-beta跟踪器获得了系统的理想状态。

本文作者针对传统控制方法对并联机器人轨迹精度控制难的问题，提出了一种基于动力学补偿的6-DOF并联机器人鲁棒轨迹跟踪控制方法，并通过MATLAB仿真实验验证其性能。

1 并联机器人的动力学模型

文中研究的6-DOF并联机器人由动平台、静平台和六条结构相同的支链组成，每根驱动杆上下关节分别采用虎克铰与上下平台相连接，图1所示为机构坐标系简图。

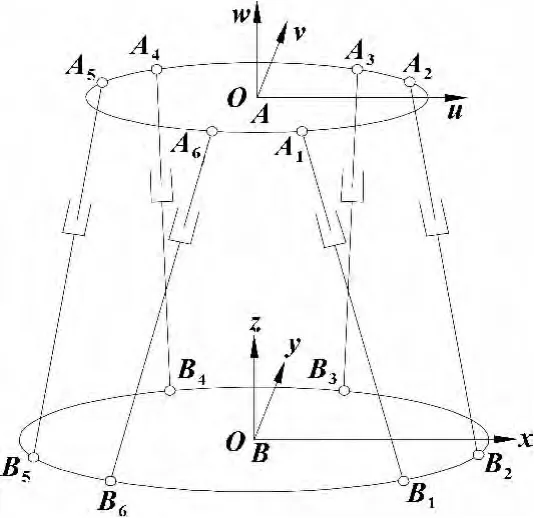
图1 机构坐标系简图

假定动平台的广义坐标用q表示，通过计算可以获得其位姿q=［x y z α β λ］T，采用Lagrange法对6-DOF并联机器人的动力学进行建模时，其Lagrange方程可写为:

2 基于逆向力补偿的控制器设计

2.1 逆向力补偿控制器的设计

采用Newton-Euler法推导机器人的逆向力是比较方便的，运用此方法对六条分支杆件的动力学特性进行补偿，则当M2、C2、G2数值并不知道的条件时，也可对系统进行控制器的设计。所以针对逆向力补偿的方法跟机器人的动力学模型有着很大的关系。文献［9］简单介绍了关于逆向力补偿控制器的设计方法，并将此方法应用于6-DOF并联机器人中，最后针对此方法进行了仿真实验，其外回路采用了PID控制，文中针对外回路采用了PD控制。

根据上述求得的动力学模型，对其采用比例微分控制，其规则为:

式中:λmax表示空间状态矩阵的最大特征值，且‖X‖是由机器人的模型误差和外界不确定性因素‖σ‖所决定，所以为了减小机器人的轨迹跟踪误差，下面设计一种鲁棒控制器应对其带来的影响。

2.2 鲁棒轨迹跟踪控制器的设计

根据补偿后的式 (6)对并联机器人设计一个鲁棒控制器，主要是为了当系统存在模型误差和外界不确定性因素的影响下，系统仍然具有鲁棒稳定性。

当机器人存在建模误差和外界不确定性因素干扰时带来的影响，则动力学方程可写为:

其中，ε、ρ表示任何给定的大于零的常数。

基于逆向力补偿的并联机器人闭环系统控制框图见图2所示。Gc表示鲁棒轨迹跟踪控制器，GI为基于逆向力的补偿控制器。

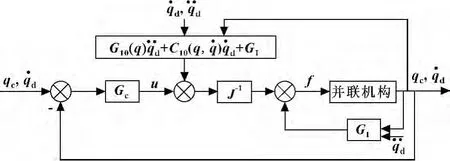
图2 闭环系统控制框图

2.2.1 系统设计指标

通过上述详细的分析可知系统对干扰d的抑制性能达到了设计的要求。

3 仿真实验研究

文献 ［9－10］基于MATLAB中的 SimMechanics模块对并联机器人的控制系统结构模型进行了搭建，并进行了仿真分析，文中也将采用此方法对6-DOF并联机器人进行控制仿真研究。

假设并联机器人动平台的运动轨迹如下所示。

图3和图4分别为采用PD控制与基于逆向力补偿的鲁棒轨迹跟踪控制时，并联机器人分别沿XYZ方向的误差仿真曲线。

图3 动平台沿XYZ方向的轨迹跟踪误差 (PD控制)

图4 动平台沿XYZ方向的轨迹跟踪误差 (鲁棒控制)

通过对上述仿真图形的分析，可以观察出当系统存在建模误差和外界不确定性因素干扰时，基于逆向力补偿的鲁棒轨迹跟踪控制在精度上相对于传统的采用PD控制要高出50%左右，因此，当采用逆向力补偿的鲁棒轨迹跟踪控制时，系统具有较高的轨迹跟踪精度和鲁棒稳定性。

4 总结

文中提出的基于动力学补偿的6-DOF并联机器人鲁棒轨迹跟踪控制方法，解决了机器人系统存在动力学建模误差和外界不确定性因素干扰的问题，文中分别通过PD控制和基于动力学补偿的鲁棒轨迹跟踪控制对并联机器人的运动进行了仿真研究，仿真结果证明，所提出的基于动力学补偿的鲁棒轨迹跟踪控制在性能上远远优于传统的PD控制。值得推广使用。

［1］GAO Z，ZAHNG D.Design Analysis and Fabrication of a Multidimensional Acceleration Sensor Based on Fully Decoupled Compliant Parallel Mechanism［J］.Sensors and Actuators A:Physical，2010，163(1):418 －427.

［2］朱大昌，刘运鸿，冯文结.3-RPC型并联机器人模糊PID控制系统研究［J］.机械传动，2014，38(2):114 －117.

［3］高秀兰，鲁开讲，郭旭侠.并联机构非线性PID自适应控制［J］.机械设计与制造，2012，12(12):125 －127.

［4］应舜安，林桐.平面二自由度冗余驱动并联机器人的鲁棒控制［J］.福州大学学报:自然科学版，2005，33(4):487－490.

［5］周兵，许艳.并串联复合机器人的一种鲁棒控制［J］.湖南大学学报:自然科学版，2005，32(1):6 －9.

［6］吴军，李铁民，唐晓强.平面并联机构的鲁棒轨迹跟踪控制［J］.清华大学学报:自然科学版，2005(5):17.

［7］赵东亚，李少远，高峰.六自由度并联机器人分散鲁棒非线性控制［J］.控制理论与应用，2008，25(5):867 －872.

［8］KIM H S，CHO Y M，LEE K.Robust Nonlinear Task Space Control for 6 DOF Parallel Manipulator［J］.Automatica，2005，41(9):1591 －1600.

［9］傅绍文，姚郁.带有逆向力补偿的Stewart平台自适应鲁棒控制［J］.电机与控制学报，2007，11(1):88－92.

［10］袁立鹏，董彦良，赵克定，等.基于动力补偿的液压并联运动平台控制策略［J］.北京航空航天大学学报，2006，32(8):941－945.

Robust Trajectory Tracking Control of Parallel Robots Based on Dynam ics Com pensate

ZHU Longying1，CHENG Lei2，ZHENG Shuai3，LU Baofa4，HE Jianli2
(1.School of Automotive Engineering of Yancheng Institute of Technology，Yancheng Jiangsu 224051，China;2.School of Mechanical Engineering of Changzhou University，Changzhou Jiangsu 213164，China;3.School of Mechanical Engineering of Anhui University of Science and Technology，Huainan Anhui232001，China;4.School of Mechanical Engineering of Jiangsu University，Zhenjiang Jiangsu 212013，China)

The problem of dynamicsmodel error and uncertainty outside interference of 6-DOF parallel robot，a robust trajectory tracking control strategy of parallel robot based on dynamics compensate was proposed.The robust control law of parallel robot via Lyapunovmethod based on the full study of dynamicmodelwas got，a robust trajectory tracking controlmethod was designed and the inner loop was compensated by inverse dynamics and the outer loop was controlled by PD，the robust controller of parallel robot was designed，the trajectory tracking control of the system was simulated via MATLAB.Simulation results prove that the trajectory tracking error uniform ly and ultimately bounded in case of periodic interferential signal，and improve the robuststability of closed-loop system to a certain extent.

Parallel robot control;Dynamics compensate;Lyapunovmethod;Robust tracking control

TP242

A

1001－3881(2015)21－078－5

10.3969/j.issn.1001 －3881.2015.21.018

2014－07－22

朱龙英 (1962—)，女，博士，教授，研究生导师，主要从事机器人技术研究。E－mail:chenglei162715@163.com。