全闭环伺服机器人正运动学的研究

刘乐，韩建海

(河南科技大学机电工程学院，河南洛阳 471003)

全闭环伺服机器人正运动学的研究

刘乐，韩建海

(河南科技大学机电工程学院，河南洛阳 471003)

对于在各关节上采用编码器的伺服控制的机器人，虽然结构简单，但是由于各关节实际响应的结果与编码器反馈存在误差，所得的末端位姿的精确位置难以确定。为此，在很多场合下，都希望通过某种外部位姿直接给定手臂末端位姿的运动，实现机器人全闭环的伺服控制，但是由于牵扯到坐标系的变换，通常的基于关节伺服的齐次坐标变换矩阵无法直接使用，本文作者给出一种数学方法，利用该方法，可方便地推导各种坐标系间的变换矩阵，并且给出了全闭环伺服系统的正运动学及其研究方法。

坐标系变换;全闭环伺服机器人;正运动学;群论

0 前言

关节伺服控制的机器人是基于各个关节独立进行控制的，虽然它们结构简单，但是由于各关节实际的响应的结果未知，所得的末端位姿的响应就难以预测，而且为了得到适当的末端响应，对于各关节的伺服系统的增益进行调节也很困难，这时需要使用全闭环伺服来控制机器人。而一般的对于全闭环伺服机器人采用半闭环控制、全闭环位置反馈的混合闭环方式进行［1］，但是这种控制方式可能会由于各关节运动控制的误差和传感器测量误差的积累从而使得整体控制的运动平稳性相对变差，并且随着关节数目的增长问题将会更加严重，因此对于多关节的闭环控制伺服机器人采用全闭环控制和全闭环反馈的完全闭环机器人系统在理论上将会获得更好的效果，但是它的运动学推导和研究却很少有人关注，混合闭环系统与完全闭环系统的系统框图如图1。

而对于各类直角坐标系的变换，前人曾做了大量的基础性的研究工作，而且由于直角坐标系的变换在卫星定位上的巨大的实用价值，而在GPS导航和定位中得到了充分的研究和利用，其中基于Bursa-Wolf模型、Molodensky Badekas模型、KrakivskyThomson模型、Veis模型的坐标变换方法［2］得到大量的研究者的关注，已经有人将理论进行了简化并且编制出使用的程序［3－5］，这些模型大多数含有7个转换参数即3个平移参数，3个旋转参数和1个缩放因子［5］，这与所要研究的机器人的平移和旋转相对应，但是，上述研究主要偏向于导航，而与机器人的运动学关系不大，下面将通过一些基本的公式和原理来推导全闭环机器人的运动学。

图1 混合闭环系统与完全闭环系统的系统框图

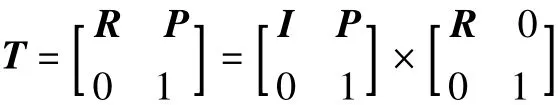
也就是说任意一个齐次坐标变换群可以分解为一个正规子群旋转群和一个子群平移群的半直积，若记旋转群为Rot，平移群为Tv，则T=Rot×Tv。因此任意一个齐次坐标矩阵都可以使用一个平移矩阵和一个旋转矩阵来表示，也就是说任意一个空间的坐标变换都可以分级为一个平移变换与一个旋转变换。

根据因果关系原理，坐标系On的姿态必然可以表示为由坐标系O0至On－1中的一个坐标系经过旋转矩阵Rn旋转而得。定义坐标系On的姿态是由坐标系On－1相对于坐标系Oi旋转而得，而坐标系 On－1可以由下式确定:

式中的R'k是坐标系On－1式中旋转矩阵经过重排

1 数学模型、基本假设和基本定义

对齐次坐标变换矩阵进行分解得序后位于位置k的旋转矩阵。

而这个公式与文献 ［6］中的吻合。

(2)当坐标系On相对于机架坐标系O0进行平移和旋转时

则由式 (1)可得此时的平移公式:

由式 (2)可得此时的旋转公式:

2 完全闭环伺服控制机器人的运动学

所以相对于动坐标系进行坐标变换时。齐次坐标矩阵右乘，相对于静坐标系进行坐标变换时齐次坐标矩阵左乘的传统的结论是不正确的。从位移方程式的平移项即可了解。

结论也是不正确的，这是由于一般的旋转矩阵属于SO(3)群，而SO(3)群为非阿贝尔群，所以两个变换式 (12)与式 (13)一般不同，但是当他们绕着同一个轴旋转时，旋转阵退化为SO(2)群，而SO(2)群为阿贝尔群，此时式 (12)与式 (13)相同。

3 实验验证

实验基于Matlab2010b和Mupad实现，实验的坐标变换阵有两个T1为绕z轴旋转π/2，平移向量为［2 1 3］，T2为绕y轴旋转π/2，平移向量为 ［2 0 4］，变换前后的世界坐标系保持不变，并且已经在坐标轴上给予显示，而空间中的动坐标系则在图中使用红色箭头 (x轴)，绿色箭头 (y轴)，蓝色箭头(z轴)表示，结果如下。

初始的坐标定义如图2所示。

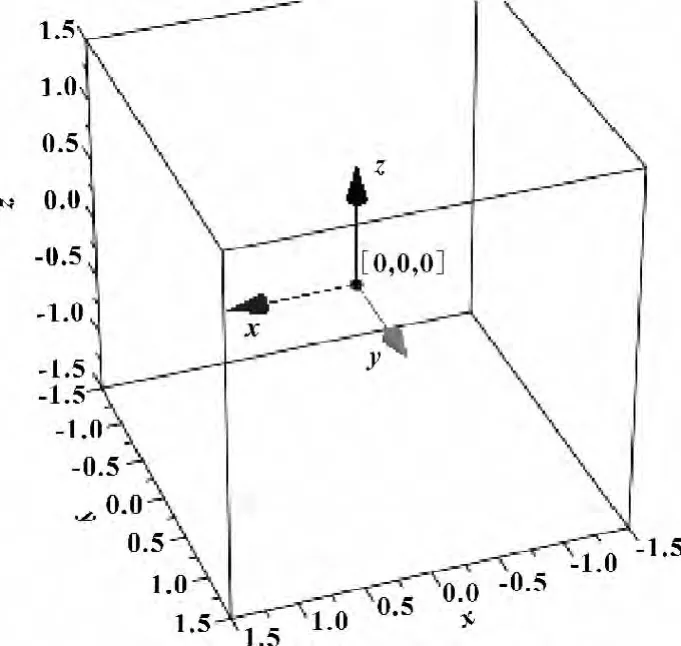
图2 初始坐标系定义

(1)当坐标系On相对于坐标系On－1进行平移和旋转时

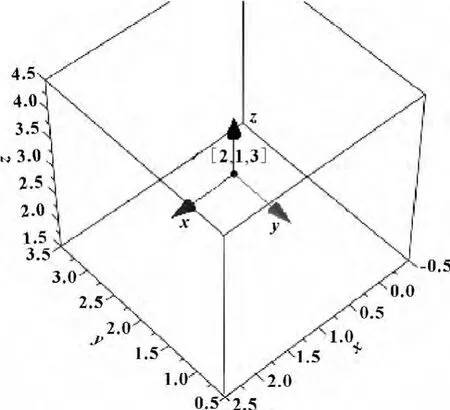
图3 对初始坐标系使用T1变换时的结果m1

图4 对m1坐标系使用T2变换时的结果

从图中可知，在相对于坐标系On－1进行坐标系变换时 (也就是传统的工业机器人所使用的坐标系)，与其他资料上的公式吻合良好，可以充分说明上述公式的正确性。

(2)当坐标系On相对于机架坐标系O0进行平移和旋转时

图5 对初始坐标系使用T1变换时的结果m1

图6 对m1坐标系使用T2变换时的结果

从图中可知，在相对于坐标系O0进行坐标系变换时 (也就是完全闭环机器人的坐标系)，结果与常识吻合良好。

4 结论

给出一种数学方法推导各种坐标系的变换矩阵，并且推导了不同坐标系的齐次坐标变换矩阵。最后由齐次坐标变换矩阵得出了基于固定坐标系和运动坐标系的位移方程式，从理论上得到了全闭环伺服机器人的正确的正运动学方程式。

［1］田文罡，陈学东，苏军，等.六足步行机器人的多关节协调控制［J］.机器人技术与应用，2009(6):33－37.

［2］KUTOGLUHakan S，MEKIK Cetin，AKCIN Hakan.A Comparison of Two Well Known Models for 7-Parameter Transformation［J］.The Australian Surveyor，June 2002，47(1):24－30.

［3］李树奎，杜国明，李秀海.进行GPS坐标成果转换及精度分析的两种方法［J］.煤炭技术，2004，23(7):89 －90.

［4］张萌，杨志勇，丁克良.基于改进的布尔莎－沃尔夫模型的任意旋转角坐标转换方法的研究［J］.北京测绘，2013，108(1):20 －23.

［5］陈宇，白征东，罗腾.基于改进的布尔沙模型的坐标转换方法［J］.大地测量与地球动力学，2010，30(3):71 －73.

［6］韩建海.工业机器人［M］.武汉:华中科技大学出版社，2009:52.

Research about Direct K inematics of Full Close-loop Servo Control Robot

LIU Le，HAN Jianhai
(School ofMechatronics Engineering，Henan University of Science and Technology，Luoyang Henan 471003，China)

The servo control of robot based on the encoder on the joint has a sample structure，but the actual response of every joint has a small difference with the encode value，so the precise position of the end of the robot is difficult to determine.For this reason，in many situations，the precisemotion of the end of the robotarm was expected to get directly in certainmethods from external position，so as to realize the full close-loop servo control of the robot，however，due to the coordinate transform concerned，the traditional method was not able to be applied to it directly based on homogeneous coordinate transform matrix of the servo joints.A mathematical method is given for using，which can easily deduce all kinds of coordinate transform matrix，and give the directkinematics of full closeloop servo control system and its researchmethod.

Coordinate transform;Close-loop servo control robot;Direct kinematics;Group theory

TP242.2

A

1001－3881(2015)21－074－4

10.3969/j.issn.1001 －3881.2015.21.017

2014－09－14

刘乐 (1989—)，男，硕士，研究方向为机器人。E－mail:qaqa1456@sina.com。