双材料界面裂纹的加料有限元方法*

杨军辉，雷勇军，蒙上阳

(1.国防科技大学航天科学与工程学院，湖南长沙410073;2.中国人民解放军63961部队，北京100012)

由多相物质组成的新材料在工程上的应用日益增多，不同材料的宏观结构之间存在着界面，因此，工程结构中的界面是广泛存在的:如固体火箭发动机壳体/绝热层、绝热层/衬层(包覆层)、衬层/推进剂药柱之间的界面，复合材料、多相材料中的异质界面等。界面是各种组合结构最薄弱的地方，往往容易产生裂纹，裂纹在一定条件下的不稳定扩展将导致组合结构的解体，因此，界面问题变得越来越重要［1］，而如何精确求解应力强度因子等断裂参量是界面断裂问题的重要内容。计算界面裂纹应力强度因子常用的方法主要有权函数法［2］、边界元方法［3］、奇异有限元方法［4］和扩展有限元法［5］等数值方法。加料有限元方法最早由Benzly［6］提出用于解决单相材料的断裂力学问题。1985年Chen［7］首先采用加料有限元法解决双材料界面裂纹问题，通过在12节点四边形单元引入加料项构造了加料界面裂纹元，但加料单元与常规单元之间没有采用过渡单元。此后，Bayram［8］将加料单元与罚函数结合解决基于接触模型的界面裂纹问题，段静波［9］等将加料单元应用于粘弹性材料，研究了单相线粘弹性材料中的断裂问题。Chen等的方法较好地求解了双材料界面裂纹的应力强度因子，但工程应用不便，且不能直接应用于斜界面裂纹。

1 界面裂纹加料单元位移模式

1.1 加料裂尖单元

加料单元包括加料裂尖单元以及为了保证加料单元和常规单元位移协调一致而引入的过渡单元。图1所示双线弹性材料界面裂纹ν2分别表示材料1和材料2的弹性模量和泊松比)，在裂尖直角坐标系x'o'y'中，裂纹尖端位移场表达式如下［7］:

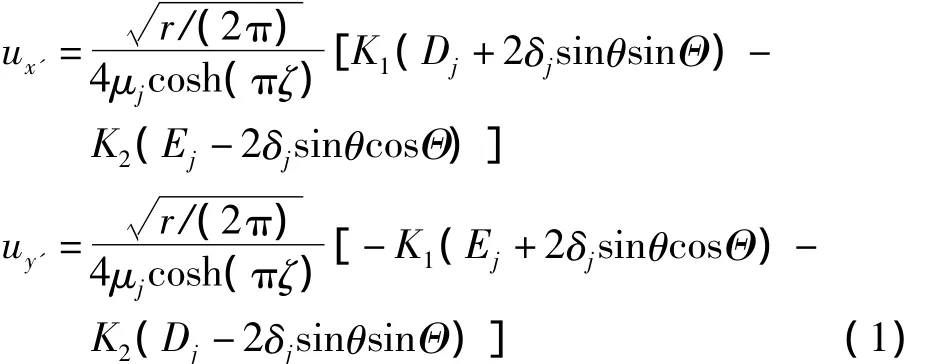
图1 界面裂纹坐标系Fig.1 Interfacial crack coordinate

其中，ux'，uy'为x'和y'方向的位移，r，θ为裂尖局部极坐标下的径向和周向坐标，下标j表示两种不同的材料(j=1，2)，μ为剪切模量，K1，K2为界面裂纹张开型和滑开型模态的应力强度因子(Stress Intensity Factor，SIF)，ζ为结合材料的振荡指数，定义如下:

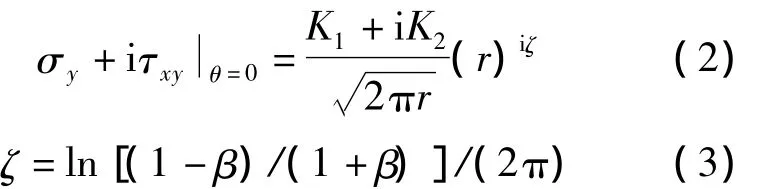
Dundurs参数为:

其中，κ为Kolosov常数，对于平面应力κ=(3-ν)/(1+ν)，对于平面应变κ=3-4ν，式(1)中其他参数表达式如下:

将裂尖渐进位移场加入到相应的常规单元位移场中，需要进行坐标变换，把裂尖直角坐标系x'o'y'中的位移ux'，uy'变换为整体坐标系xoy中的位移ux，uy，变换关系式如下:

其中，(xo'，yo')为裂尖在整体坐标系中的坐标。对于4节点四边形等参元，在常规位移模式中加入界面裂纹裂尖渐进位移项后，可得:

其中，ui(i=1，2)分别表示总体坐标系下加料界面裂纹单元x，y方向的位移，ξ，η分别为单元局部坐标系的坐标轴，fij(r，θ)为裂尖角函数，根据界面裂纹的裂尖渐进位移场表达式，有:

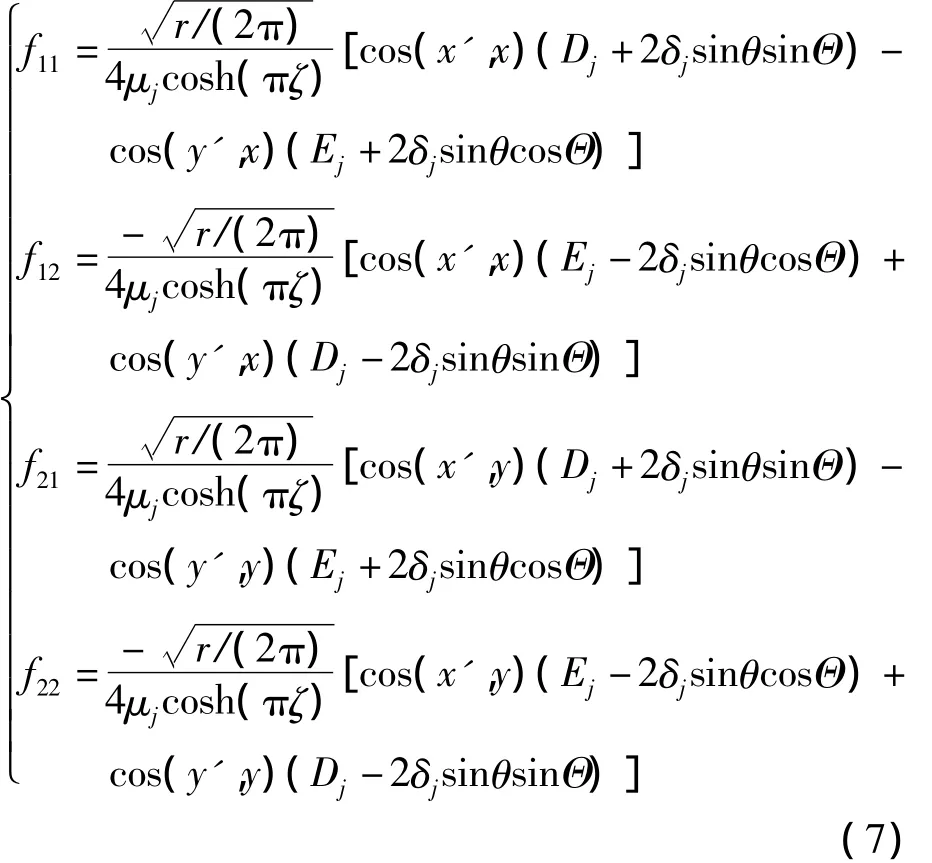
将4节点四边形等参元的节点局部坐标(ξi，ηi)代入式(6)中，可得到广义坐标αij的表达式，再将得到的广义坐标回代到式(6)中，得到加料界面裂尖单元的位移模式如下:

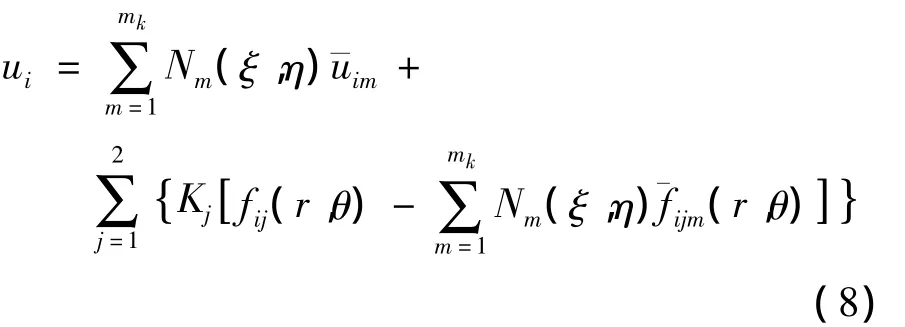
其中，Nm(ξ，η)为常规等参元形函数，mk为单元节点数为第m个节点处的节点位移值θ)为角函数fij(r，θ)在第m个节点处的函数值，Kj为附加节点自由度，即界面裂纹应力强度因子。

1.2 过渡单元

在加料裂尖单元和常规单元之间采用过渡单元，以消除两种单元因位移模式引起的位移不协调问题，从而保证有限元解得收敛，提高计算精度。在加料裂尖单元位移模式的基础上，引入一个调整函数Z(ξ，η)来构造过渡单元内位移模式，即:

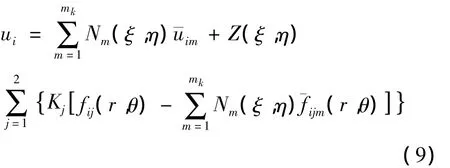
其中，调整函数Z(ξ，η)须满足:Z(ξ，η)在过渡单元与加料裂尖单元交界边上为1，在过渡单元与常规单元交界边上为0，实现从加料裂尖单元到常规单元的协调过渡。采用相对简单的线性调整函数:

在有限元分析过程中，需要根据过渡单元与加料裂尖单元的连接方式以及过渡单元的局部坐标系，选择适当的表达式。例如，当过渡单元的边ξ=1与加料裂尖单元连接时，满足条件的调整函数Z(ξ，η)表达式为Z(ξ，η)=0.5(1+ξ)。

2 有限元方程

为了便于推导有限元方程，将加料单元、过渡单元位移模式统一写成如下向量形式:

其中:N是常规单元形函数，是节点位移列向量;N k加料单元或过渡单元的附加形函数附加自由度向量。N k的具体形式如下:

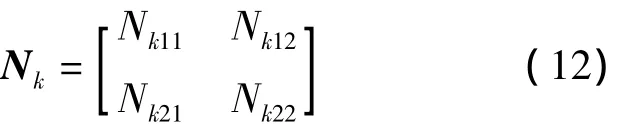
对于加料单元Z(ξ，η)≡1，过渡单元按式(9)取值，将位移向量式(11)代入位移应变关系中，得到:

其中，B表示单元常规应变矩阵，B k则是由于加料界面裂纹单元位移模式中引入裂纹尖端位移项而产生的附加项，称之为加料裂纹元附加应变矩阵。将式(13)代入单元应力应变关系式式中，应用总体势能泛函为:

其中，b为体力，P为面力，Ω表示求解域，Γ为面力积分边界，D为材料矩阵，取值依据界面两侧材料具体参数确定，可得到:

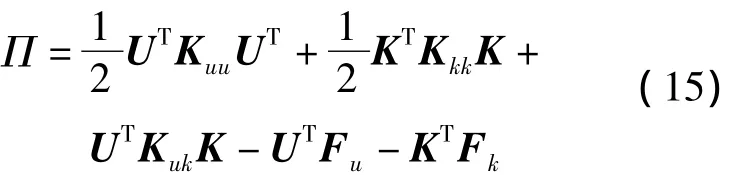
其中，U为总体位移列阵，K为应力强度因子列阵，其他符号表达式如下:

其中，ns表示加料单元数量，nt表示过渡单元数量，no表示常规单元数量，上标e表示单元，根据最小势能原理，式(15)分别对U，K变分，得到有限元方程如下:

3 加料单元在界面裂纹中的应用

为便于对比分析，本节不涉及物理单位。

3.1 中心界面裂纹

对含中心界面裂纹的弹性体承受均布拉力的问题，按平面应变进行了计算。其中，y轴单向受拉如图2所示，x，y轴双向受拉如图3所示。裂纹长度a=2，有限元建模时，取平板边长b=10a，近似满足无限大条件。根据对称性，取1/2模型建模，裂尖局部网格适当加密(网格尺度l/a=1/40)，共划分为800个4节点四边形单元，850个节点。为了考察加料单元和过渡单元的配置区域对计算精度的影响，采用两种配置方案:第1种方案是在上半平面(y〉0，对应材料1)配置2个加料单元，4个过渡单元(如图4所示);第2种方案是在上半平面配置6个加料单元，4个过渡单元(如图5所示)，两种方案下半平面(对应材料2)均采用与上半平面同样的配置。计算单元刚度矩阵时，加料单元和过渡单元用8×8高斯积分，常规单元采用2×2高斯积分。

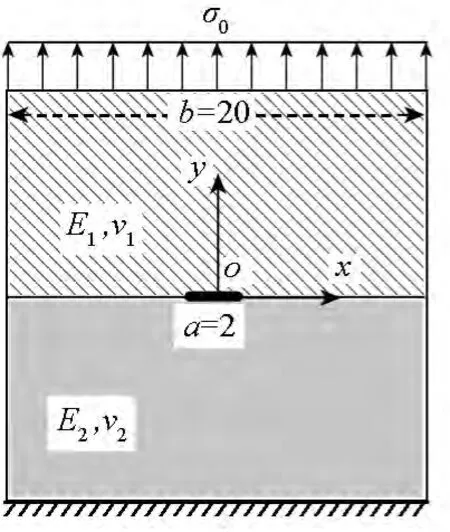
图2 单向受拉工况Fig.2 Uniaxial tensile load case

图3 双向受拉工况Fig.3 Biaxial tensile load case

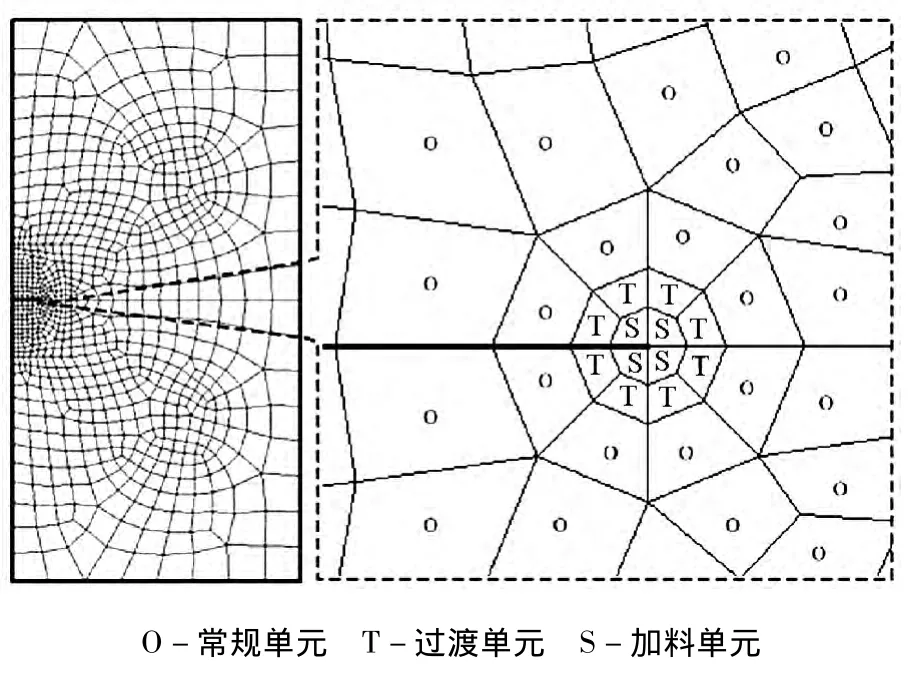
图4 加料单元和过渡单元配置方案1Fig.4 Scheme one of enriched element and transition element

双向受拉工况材料参数和载荷取值见表2，应力强度因子计算结果以及和文献［7］对比结果见表3。

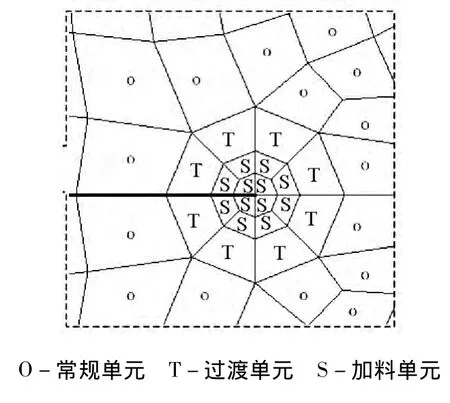
图5 加料单元和过渡单元配置方案2Fig.5 Scheme two of enriched element and transition element

表2 材料参数及载荷工况Tab.2 Material parameters and load cases

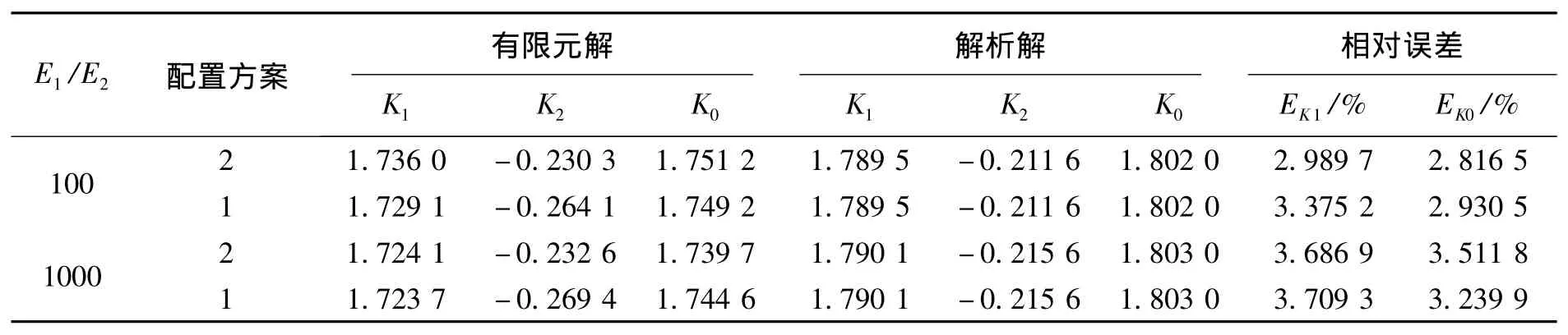
表1 单向受拉应力强度因子Tab.1 Stress intensity factor values of uniaxial tensile load

表3 双向受拉应力强度因子Tab.3 Stress intensity factor values of biaxial tensile load

文献［7］加料单元和常规单元均为12节点四边形单元，但加料单元和常规单元之间没有采用过渡单元。由对比结果可见，在各种工况下，K1，K2计算值与文献［7］相差均不超过5%，K0的相对误差不超过1%。与K1相比，K2误差相对较大，经分析，文献［7］K2计算值与准确结果相比误差较大，而加料有限元法K2计算值与准确结果更接近。K2准确值可参考文献［10］，该文献应用17节点应力杂交元，保留了应力场渐进解的前16项，其计算结果是相当准确的，与加料有限元法对比结果见表4。因此，尽管有限元模型没有采用高阶单元，但由于应用了加料单元和过渡单元，并在裂纹局部网格适当加密，仍达到了令人满意的计算精度。以上两个算例表明，有限元模型及计算方法对界面裂纹问题是有效的，能方便地给出应力强度因子的正确结果。

表4 K2对比结果Tab.4 Compare results of K2

3.2 斜界面裂纹

受均匀拉伸的具有斜单边界面裂纹的矩形板如图6所示，b=2，a/b=0.5，裂纹倾斜角为θ。材料1和材料2的泊松比固定为0.3，则结合材料参数只与弹性模量E1，E2有关，将E2固定为1，E1取不同值，可得到不同的结合材料参数，按平面应变计算斜界面裂纹应力强度因子。

当E1=E2时，退化为单相材料矩形板单边斜裂纹问题，单向拉伸即可产生Ⅰ，Ⅱ复合型应力强度因子，当θ=45°，a/b=0.5时，计算结果为K1=1.208，K2=-0.572，与文献［11］结果一致。

当E1取值从1变化到1000时，振荡指数变化区间为(0，0.0934)，分别计算了a/b=0.5，裂纹倾角分别为45°，67.5°以及裂纹倾角为45°，a/b分别等于0.3，0.5时K0和模态比(K2/K1，Modal Ratio，MR)的值。

为了便于比较分析，将K0变形为K0=F0σ为横坐标，F0为纵坐标做出变化曲线。图7是θ=45°，a/b=0.5时的有限元模型，采用4节点四边形单元，单元数量为1250个，节点数量为1227个，裂纹倾角为67.5°以及裂纹长度为0.3b时单元数量分别为1255个和1327个。根据计算结果绘制的曲线如图8～11所示。

图6 双材料矩形板单边斜界面裂纹Fig.6 Bimaterial rectangular plate unilateral oblique interface crack

图7 斜界面裂纹加料有限元模型Fig.7 Unilateral oblique interface crack EFE model

由图8～11可见，在各种不同裂纹长度和倾角下，随着结合材料振荡指数的增大，复合应力强度因子的模逐渐减小，而模态比的绝对值则逐渐增大，说明界面两侧材料的差异性增强了剪切效应，并且裂纹倾角越大，模态比曲线变化越明显，表明界面导致的KⅡ变化越大，这与马开平等［12］用半权函数法得到的结果是一致的。由图10、图11可见，界面裂纹倾角相同的情况下，裂纹长度越小，复合应力强度因子越小;并且与裂纹倾角相比，由裂纹长度变化而引起的剪切模态KⅡ变化较小。

图8 不同裂纹倾角下SIF计算结果Fig.8 SIF for different crack angles

图9 不同裂纹倾角下MR计算结果Fig.9 MR for different crack angles

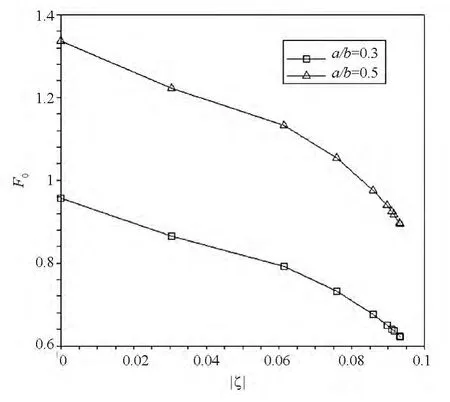
图10 不同裂纹长度下SIF计算结果Fig.10 SIF for different crack lengths

图11 不同裂纹长度下MR计算结果Fig.11 MR for different crack lengths

4 结论

1)通过在常规单元位移模式中引入界面裂纹渐进位移场，得到了界面裂纹加料单元和过渡单元的位移模式，推导了界面裂纹加料有限元方程，对一般界面裂纹平面问题进行了计算，结果表明应力强度因子数值解的精度满足工程要求。

2)应用加料单元和过渡单元后，即使采用低阶线性单元，网格划分规模相对较小的情况下，也能得到较为精确的应力强度因子数值解。一般而言，应力强度因子主要模态的精度要好于次要模态的精度，加料单元和过渡单元的配置方式对应力强度因子计算精度有一定的影响，但对于主要模态和复合应力强度因子精度的影响不大。

3)加料有限元方法可直接从有限元方程求解得到应力强度因子，不再需要通过单元节点位移或单元应力插值的方式获取，是处理界面断裂问题的一种快速、有效的计算方法。

References)

［1］许金泉.界面力学［M］.北京:科学出版社，2006.XU Jinquan.The mechanics of interface［M］.Beijing:Science Press，2006.(in Chinese)

［2］Gao H J.Weight function method for interface crack in anisotropic bimaterials［J］.International Journal of Fracture，1992，56(2):139-158.

［3］He W J，Bolander J E J，Lin D S，et al.A boundary element for crack analysis at a bimaterial interface［J］.Engineering Fracture Mechanics，1994，49(3):405-410.

［4］Wu Y L.Variable power singular interface elements for a crack normal to the bimaterial interface［J］.Engineer Ingfracture Mechanics，1994，48(6):763-772.

［5］Sukumar N，Huang Z Y，Prévost J H，et al.Partition of unity enrichment for bimaterial interface cracks［J］.International Journal for Numerical Methods in Engineering，2004，59(8):1075-1102.

［6］Benzley S E.Representation of singularities with isoparametric finite elements［J］.International Journal for Numerical Methods in Engineering，1974，8(3):537-545.

［7］Chen E P.Finite element analysis of a bimaterial interface crack［J］.Theoretical and Applied Fracture Mechanics，1985，3(3):257-262.

［8］Bayram Y B，Nied H F.Enriched finite element-penalty function method for modeling interface cracks with contact［J］.Engineering Fracture Mechanics，2000，65(1):541-557.

［9］段静波，雷勇军.线粘弹性材料中三维裂纹问题的加料有限元法［J］.国防科技大学学报，2012，34(3):6-11.DUAN Jingbo，LEI Yongjun.The enriched finite element method for 3-D fracture problems in viscoelastic materials［J］.Journal of National University of Defense Technology，2012，34(3):6-11.(in Chinese)

［10］Lin K Y，Mar J W.Finite element analysis of stress intensity factors for cracks at a bi-material interface［J］.International Journal of Fracture，1976，12(4):521-531.

［11］中国航空研究院.应力强度因子手册［M］.北京:科学出版社，1981.China Aeronautical Establishment.Stress intensity factor handbook［M］.Beijing:Science Press，1981.(in Chinese)

［12］马开平，柳春图.双材料界面裂纹平面问题的半权函数法［J］.应用数学和力学，2004，25(11):1135-1142.MA Kaiping，LIU Chuntu.Semi-weight function method on computation of stress intensity factors in dissimilar materials［J］.Applied Mathematics and Mechanics，2004，25(11):1135-1142.(in Chinese)