基于LMD近似熵和SVM的自适应重合闸方法*

江亚群，冷崇富，黄 纯，戴栩生

(湖南大学 电气与信息工程学院，湖南 长沙 410082)

基于LMD近似熵和SVM的自适应重合闸方法*

江亚群†，冷崇富，黄 纯，戴栩生

(湖南大学 电气与信息工程学院，湖南 长沙 410082)

自适应重合闸的功能是快速、准确地辨识故障性质及捕捉电弧熄灭时刻.在分析瞬时性故障和永久性故障断路器跳闸后的端电压波形复杂性的基础上，提出了局部均值分解(LMD)、近似熵和线性支持向量机(SVM)相结合的自适应重合闸整体实现方案.利用LMD分解故障信号得到若干个PF分量，选取前3个PF分量算出其近似熵值构成三维特征向量，将三维特征向量作为SVM的输入量来区分故障性质和捕捉电弧熄灭时刻.线路故障仿真结果表明，该方案可智能识别故障性质和捕捉电弧熄灭时刻且具有一定的抗噪能力.

自适应重合闸；局部均值分解；近似熵；支持向量机

超高压输电线路由于重负荷、长距离输电以及布局在室外，致使其易受自然因素的影响而发生瞬时性故障和永久性故障.运行数据表明，大多数故障为单相接地瞬时性故障.因此，超高压输电线路上普遍安装单相重合闸装置来提高输电线路供电的连续性及可靠性.单相自动重合闸装置在故障跳闸后延时一段时间就进行重合，当重合于永久性故障或未熄弧的瞬时性故障时，将造成再次冲击，可能破坏电力系统的稳定性和损坏昂贵的电气设备.为避免盲目重合带来的不利影响，自适应重合闸技术得到了广泛的研究.

区分故障性质和捕捉瞬时性故障熄弧时间是自适应重合闸实现的关键.目前故障状态区分的方法有多种.文献[1]使用离散傅里叶变换(DFT)进行谐波分析，并以奇次谐波含量大小来区分故障性质，计算量小，物理意义明显，但DFT主要适应稳态信号，计算暂态信号时误差较大且该方法易受谐波变化的影响.文献[2]利用小波能量谱区分故障性质，方法简单易于实现，但小波变换不能自适应的分解信号，且小波基的优化选取比较复杂.文献[3]利用经验模态分解(EMD)提取特征量来区分故障性质，能自适应的分解故障信号且计算速度快，但EMD分解得到的分量缺乏实际的物理意义及存在模态混淆.文献[4～5]采用神经网络对故障性质进行识别，需要大量的样本，计算速度及精度不能满足实际要求.文献[6]基于电流差动原理可实现瞬时性故障电弧熄灭判别，由于电力系统运行的复杂性，导致该方法不易实现.文献[7]采用电压幅值法区分故障性质，但易受故障地点的影响，且当输电线路上的电容耦合电压较低时存在误判的可能.文献[8～9]利用恢复电压的拍频特性识别瞬时性故障，当并联电抗器的补偿度较大时将导致判据的区分度不明显，且该方法只适应于带并联电抗器的输电线路.

本文根据不同故障性质在断路器跳闸后电弧阶段故障相端电压波形复杂度的不同进行故障性质的识别，依据瞬时性故障的电弧状态和电弧熄灭状态的故障相端电压波形复杂性的不同来捕捉电弧熄灭时刻.利用局部均值分解(Local Mean Decomposition，LMD)将故障信号分解成具有物理意义的PF分量，使用近似熵计算出PF的复杂度构成特征向量，以所得特征向量作为线性支持向量机(Support Vector Machine，SVM)的输入量来区分故障性质和捕捉熄弧时刻，提出了自适应重合闸的整体实现方案.

1 故障相端电压特征分析

在不同故障性质下，故障相端电压特征存在显著的差异.

故障相端电压U为线路首端至故障点之间的电压降ΔU和故障点电压UFault的相量和，即

在断路器跳闸后，ΔU等于非故障两相的电流在故障相上通过互感的电磁耦合产生的互感电压，由于特、超高压线路电流中谐波含量很低，因此，不管是瞬时性还是永久性故障，都可以近似认为ΔU为正弦波，只含有基波分量.

但是，对于不同性质的故障，故障点电压UFault的特征存在显著的区别.

当线路发生永久性故障时，由于故障点可靠接地，断路器跳闸后，故障电弧很快熄灭，故障点电压UFault变为0(金属性接地时)或为幅值基本不变的正弦电压(经过渡电阻接地时).

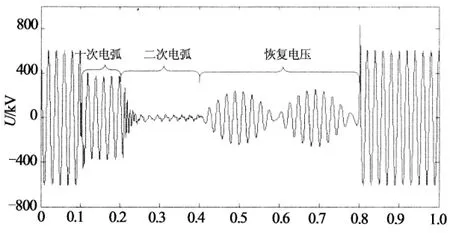
当线路发生瞬时性故障时，断路器跳闸断开故障相线路后，故障电弧并不马上熄灭，而将持续一段相对较长的时间，此时的电弧称为二次电弧.二次电弧会经过燃烧-熄灭-重燃-熄灭的反复过程.当电弧电压低于重燃电压时，电弧电流非常小，电弧处于熄灭状态；当电弧电压高于重燃电压时，电弧电流较大，电弧又开始燃烧并拉长，直到电弧电压不再大于电弧重燃电压，二次电弧才真正熄灭.在这一过程中，影响二次电弧发展的因素是复杂的和多方面的.为了研究二次电弧，国内外学者提出许多电弧模型[10]，这些模型在故障分析时起到了一定的作用.但是，由于电弧的重燃、熄灭过程非常复杂，并受许多因素影响，带有很大的随机性，现有模型均不能完全真实地模拟故障电弧，采用这些模型模拟的电弧电流和电压与实际情况也存在一定的差距.但是，有一点是可以肯定的，即二次电弧电压波形畸变非常严重，含有大量的高频分量，且各频率成分的含量不稳定，随时间变化.

在永久性故障和瞬时性故障两种情况下，故障相端电压的复杂程度明显不同.

对于永久性故障，如前所述，线路首端至故障点间的电压降ΔU和故障点电压UFault均为简单的正弦波，因此故障相端电压U也为正弦波，波形复杂度低.

对于瞬时性故障，二次电弧未熄灭前，尽管ΔU仍然基本上为正弦波，但是故障点电压UFault为二次电弧电压，其波形畸变严重，频率成分复杂且是时变的.因此，可依据跳闸后故障相电压信号的复杂度来区分永久性故障和瞬时性故障.

当瞬时性故障二次电弧熄灭后，UFault为0，故障相端U(即恢复电压)由电容耦合电压和电感耦合电压构成，其幅值比二次电弧阶段大．但电容耦合电压和电感耦合电压均为正弦电压，电压U的波形复杂度在熄弧后显著下降.以此为依据可以捕捉瞬时性故障的熄弧时刻，从而保证在故障电弧熄灭后重合闸，避免重合闸失败.基于文献[10]中提出的二次电弧数学模型，利用EMTP暂态仿真软件，搭建750kV输电线路和电弧模型，对输电线路在100ms时发生故障及200ms时断路器跳闸进行仿真，得到瞬时性故障断路器跳闸后电弧电压和故障相端电压波形分别如图1～2所示.永久性故障时，电弧模型用线性电阻替代，仿真得到故障处电压和故障相端电压波形分别如图3～4所示.仿真结果与上述分析是一致的.

时间/min

时间/min

时间/min

时间/min

2 信号的LMD近似熵

本文主要分析了瞬时性故障跳闸后电弧状态、熄弧状态和永久性故障三种故障状态.其中电弧故障状态的信号是非平稳性的，而LMD能自适应的分解复杂的非平稳信号，将其分解成若干个具有物理意义的PF分量之和，其中每一个PF分量由一个包络信号和一个纯调频信号相乘得到的，包络信号代表该PF分量的瞬时幅值，PF分量的瞬时频率可由纯调频信号求出，从而得到原故障信号完整的时频分布.不同故障状态下得到的PF分量的复杂性不同，而近似熵是采用一个非负数来表征信号序列的复杂度及不规则性，信号越复杂其近似熵值越大，它能利用较短的数据估算出信号的近似熵，具有一定的抗干扰能力，对暂态信号有较好的承受能力，因此采用LMD近似熵来获取故障状态的特征向量.

2.1 信号的LMD分解

采用LMD分解信号x(t)的步骤[11]如下：

1) 获取局部均值函数m11(t)和包络函数a11(t):

找出信号x(t)所有的局部极值点pi，求出相邻极值点的平均值mi和包络线函数值ai：

(1)

(2)

拟用折线连接相邻的均值点mi和包络函数值ai，然后采用滑动平均法对其进行平滑处理得到局部均值函数m11(t)和包络函数a11(t)．

2) 提取纯调频函数s1n(t)和局部包络函数a1n(t)．

h11(t)=x(t)-m11(t)；

(3)

s11(t)=h11(t)/a11(t)．

(4)

理想情况下s11(t)是一个纯调频函数，即a12(t)=1．否则，将s11(t)作为原信号重复以上迭代过程，直至s1n(t)成为纯调频函数，且其局部包络函数a1(n+1)(t)=1，迭代终止条件为：

(5)

为降低运算量及减少迭代次数，可以用a1n(t)≈1作为终止条件．

3) 求取PF分量的包络信号:

(6)

4) 求取PF分量

将纯调频函数s1n(t)和包络函数a1(t)相乘，可获得原信号的第一个PF分量PF1(t)：

PF1(t)=s1n(t)a1(t)．

(7)

从原信号x(t)中将PF1(t)分离出来，得到一个时间信号序列u1(t)，将其作为原信号重复上述过程，循环k次，得到：

(8)

根据上述步骤，原始信号x(t)被分解为k个PF分量和一个残余分量uk(t)，原信号x(t)为：

(9)

2.2 近似熵算法

给定信号序列{u(i)}(i=0,1,…,N)，事先给定模式维数m和相似容限r的值，{u(i)}的近似熵计算步骤[12]如下．

1)将序列{u(i)}按顺序组成m维向量X(i)为：

X(i)=[u(i),u(i+1),...,u(i+m-1)]．

(10)

2)计算向量X(i)与其余向量X(j)间的距离为：

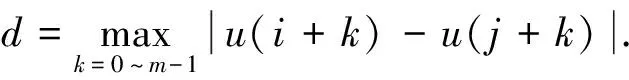
(11)

(12)

(13)

5)重复以上过程得到Φm+1(r)．

6)序列{u(i)}的近似熵为：

(14)

3 基于SVM的自适应重合闸实现步骤

每种故障状态对应的特征向量不同，因此故障状态的区分可以转化为对特征向量的分类，而SVM具有较强的学习能力，能达到智能区分故障状态的目的．依据特征向量线性可分的特点，采纳线性SVM减少了计算量，其实现方法[13]为：

设训练集T={(x1,y1)，…，(xL,yL)}，i=1，…，L，xi∈x=Rn是SVM第i个输入量，yi={1,-1}对应其期望输出值，构造二次规划问题，求出w,b

s.t.yi(w·xi+b)≥1,i=1…,L;

(15)

建立分类超平面(w·x)+b=0，得到决策函数：

y=sgn(w·x+b)．

(16)

由SVM识别输电线路故障性质以及捕捉电弧熄灭时刻的实现流程如图5所示．实现步骤为：

1)对输电线路瞬时性故障和永久性故障在断路器跳闸后进行数据采集，得到故障信号；

2)利用LMD分解故障信号，得到若干个PF分量；

3)选取主要反应故障信号的PF分量，计算出各PF分量的近似熵，分别组成反应瞬时性故障电弧熄灭与未熄灭和永久性故障的特征向量；

4)构造线性SVM1和SVM2分别识别故障性质和捕捉电弧熄灭时刻．给定永久性故障时SVM1输出为-1,瞬时性故障为+1；给定瞬时性故障未熄弧时SVM2输出+1,熄弧为-1进行训练；

5)利用训练好的SVM1对检测样本进行识别，当输出为-1时，判别故障为永久性故障跳开非故障相；当输出为+1时，判别故障为瞬时性故障，然后拟用数据窗连续采样，实时计算出特征向量输入给SVM2，当SVM2输出结果出现-1时判定电弧熄灭，为避免重合于过电压延时100ms重合．

4 算法仿真分析

4.1 故障信号的采集及LMD分解

采用文献[14]中的输电线路模型及其参数，在输电线路带与不带并联电抗器的情况下，利用EMTP对瞬时性故障和永久性故障分别在两种过渡电阻和三种故障位置进行仿真．为了避免跳闸瞬间产生的暂态分量，断路器跳闸20 ms后，以采样频率5 000 Hz对瞬时性故障的电弧状态、熄弧状态和永久性故障采集故障信号．对每一种故障状态以600个点对故障信号进行截取作为一组数据，每种故障状态收集10组．该方案研究了三种故障状态下的各6种故障情况，因此可获得输电线路带与不带并联电抗器的瞬时性故障的电弧状态、熄弧状态和永久性故障各60组故障信号．

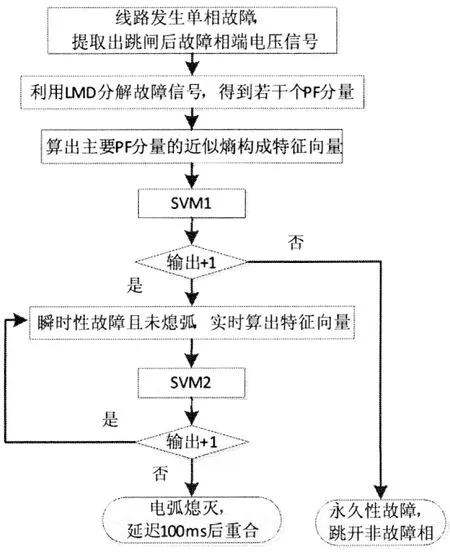
图5 自适应重合闸方案流程图

利用LMD分解上述获得的故障信号，带并联电抗器情况下，三种故障状态的各一组数据的分解结果分别如图6～8所示．

图6 电弧状态故障信号LMD分解结果

4．2 故障信号特征量提取

由LMD分解结果可知，故障信号的信息主要集中在前3个PF分量中，因此选取三种故障状态的前3个PF分量来区分故障性质以及捕捉电弧熄灭时刻.取参数m=2，r=0.25SD(u)(SD表示序列{u(i)}的标准差)，根据近似熵公式(14)计算得到ApEn1,ApEn2,ApEn3，组成特征向量X=(ApEn1,ApEn2,ApEn3)T.记瞬时性故障电弧状态获得的特征向量为样本库A，熄弧得到的特征向量为样本库B，永久性故障的特征向量为样本库C，选取带并联电抗器输电线路的6种故障情况下的每种故障状态的一组特征向量见表1.

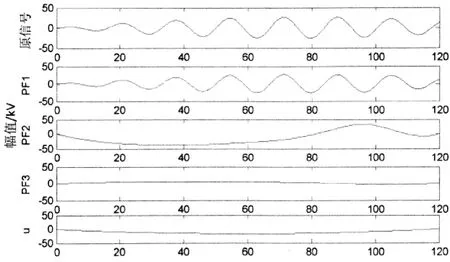
图7 熄弧状态故障信号的LMD分解结果

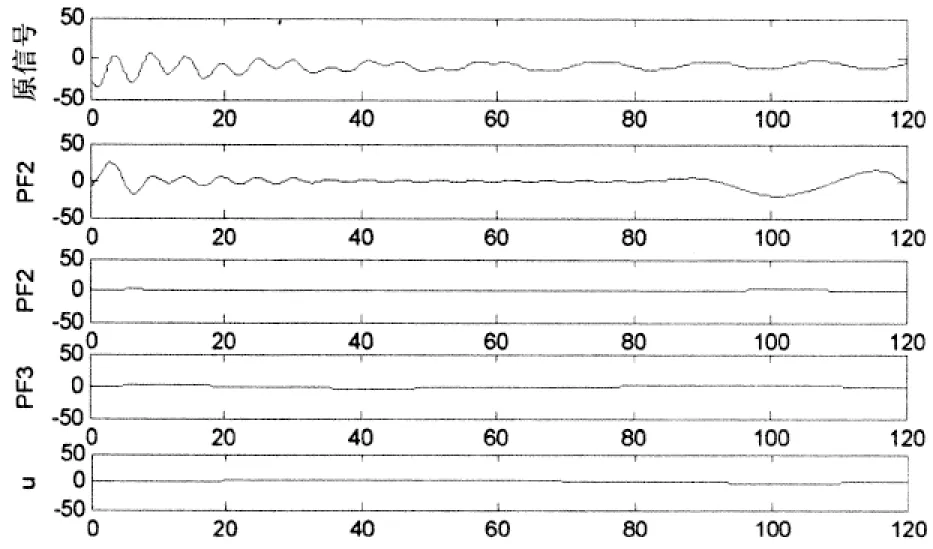
图8 永久性故障信号的LMD分解结果

从表1中可见，不同故障性质以及瞬时性故障电弧熄灭前后的近似熵值不同，且彼此间有一定的差距．虽然根据近似熵的值能反应不同的故障特征，但仅依据近似熵的大小区分故障性质及捕捉电弧熄灭时间区分度不够明显，因此将故障特征向量与SVM结合起来能达到区分故障性质及捕捉熄弧时刻的目的.

4.3 SVM的故障性质识别及电弧熄灭时刻的捕捉

从样本库A,C中各随机选取40个样本作为SVM1的训练样本，从库A,B中各随机选40个样本作为SVM2的训练样本，剩余20个作为检测样本.对于瞬时性故障，使用样本库A中的样本训练时给定SMV1的输出yi=+1；对永久性故障，使用库C中的样本训练时输出为-1.瞬时性故障情况下，电弧未熄灭时，采用库A中的样本训练时给定SVM2的输出yi=+1；电弧已熄灭，使用库B中的样本训练时输出为-1.通过对训练样本的多次训练，求解出SMV的参数w和b，获得决策函数式(16)，从而建立起特征向量与故障状态的映射关系，SVM的训练步骤如图9所示.

图9 SVM的训练步骤

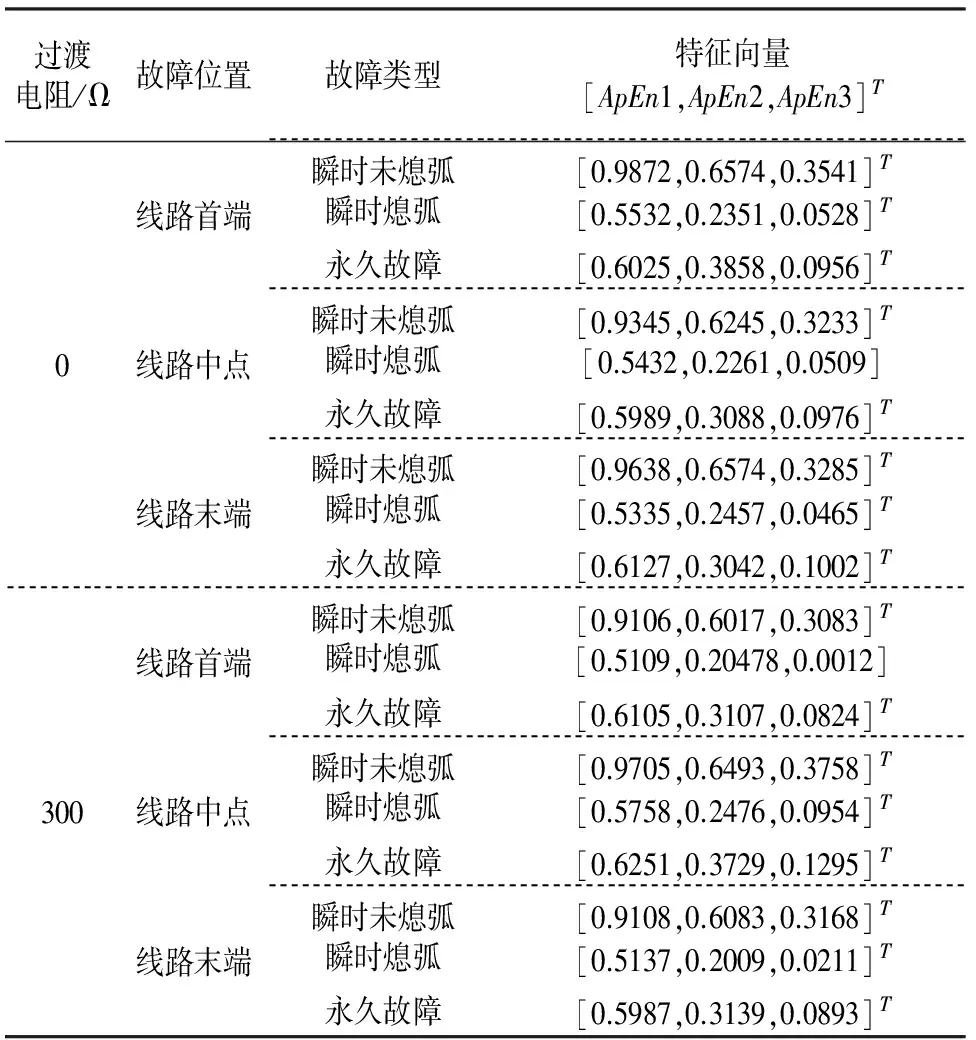
表1 不同故障信号的LMD近似熵值

输电线路发生故障时，依据上述方法获取特征向量输入已训练好的SVM1，当输出为-1时判定为永久性故障，否则为瞬时性故障．此时，采用滑动数据窗实时计算出特征向量输入SVM2，当输出出现-1时则说明电弧熄灭．为了检验小样本情况下SVM的检测精度和速度，引入BP神经网络作为比较对象；为验证SVM的鲁棒性，在检验样本中掺杂信噪比为40 db的高斯白噪声，将检测样本输入已训练好的SVM进行验证．图10为输电线路带与不带并联电抗器的A,B,C库中检测样本的SVM输出结果，表2为20个检测样本的SVM和BP神经网络识别成功率比较，表3为两者识别所需时间的比较(计算机的CPU型号是Intel酷睿i5 2430M、主频为2.4GHz，内存容量为2GB DDR3 1333 MHz)．

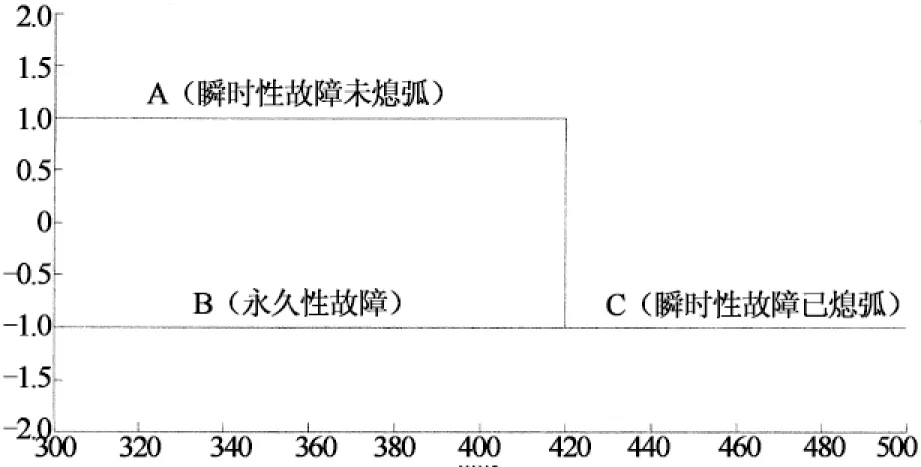
图10 检测样本的SVM输出结果

表2 SVM与BP神经网络识别成功率比较

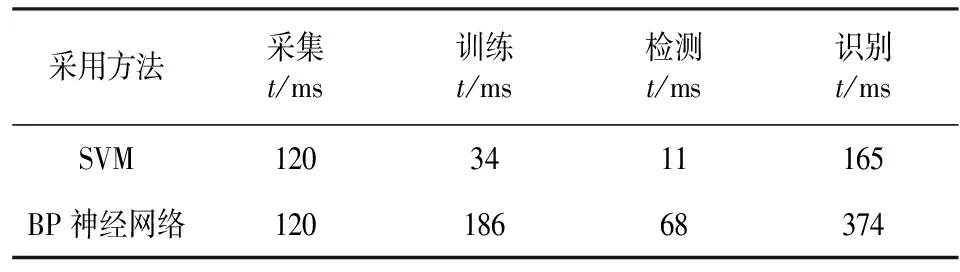
表3 SVM与BP神经网络识别时间比较

由图10及表2～3可知，基于LMD近似熵和SVM的方案能可靠、快速地识别故障性质及捕捉熄弧时刻．且由于BP神经网络识别故障时需要较多的样本，在小样本下会出现误差，而SVM适应于小样本检测，识别结果不出现误差，因此在小样本检测的情况下，SVM识别故障性质的精度比BP神经网络高，且所需时间更短．

由于特、超高压输电线路很难进行现场试验，本文从故障录波器获得500 kV线路和220 kV线路发生单相接地故障时的故障录波文件，并从录波文件提取故障线路故障相的电压录波数据，利用该数据对本文方法进行验证．结果表明，本文提出的基于LMD近似熵和SVM的自适应重合闸方法能可靠、快速地区别故障性质，并及时捕捉电弧熄灭时刻．

5 结 论

1)本文分析了瞬时性故障断路器跳闸后电弧、熄弧状态和永久性故障的故障相端电压波形的复杂性，设计了基于LMD近似熵和SVM的自适应重合闸实现方案．

2)该方案实现了同时识别故障性质和捕捉电弧熄灭时刻的功能，且同时适用于带与不带并联电抗器的输电线路，在已有的自适应重合闸判据中具有一定的优越性．

3)仿真结果表明，本文方案在小样本的情况下能准确、快速地区分故障性质及捕捉电弧熄灭时刻，具有一定的抗噪能力．

[1] 李斌，李永丽，曾治安，等. 基于电压谐波信号分析的单相自适应重合闸[J].电网技术，2002，26(10)：53-57.

LI Bin, LI Yong-li，ZENG Zhi-an,etal. Study on single-pole adaptive reclosure based on analysis of voltage harmonic signal [J]. Power System Technology，2002，26(10)：53-57. (In Chinese)

[2] 程玲, 徐玉琴, 宋秭霖. 基于电弧小波谱能量分析的输电线路单相自适应重合闸[J]. 电网技术, 2007,31(24): 81-85.

CHENG Ling，XU Yu-qin，SONG Zi-lin. Single-pole adaptive reclosure of transmission line based on arc models and wavelet spectrum energy analysis [J]. Power System Technology，2007，31(24)：81-85. (In Chinese)

[3] 兰华，艾涛，李扬. 经验模态分解在单相自适应重合闸中的应用[J]. 电力系统保护与控制，2010,38(12)：35-39.

LAN Hua，AI Tao，LI Yang. Application of EMD on single-pole adaptive reclosure of transmission [J]. Power System Protection and Control, 2010,38(12)：35-39. (In Chinese)

[4] 杨伟，彭丽，张俊芳，等. 基于模糊神经网络的自适应单相自动重合闸[J]. 继电器，2005，33(15)：66-70.

YANG Wei，PENG Li，ZHANG Jun-fang，etal．Adaptive auto-reclosure of single phase based on ANN [J]. Relay，2005，3(15)：66-70. (In Chinese)

[5] 聂宏展，董爽，李天云，等．基于模糊神经网络的单相自适应重合闸[J]. 电网技术，2005，29(10)：76-79.

NIE Hong-zhan, DONG Shuang, LI Tian-yun,etal．Single phase adaptive auto-reclosure based on fuzzy neural network [J]. Power System Technology，2005，29(10)：76-79. (In Chinese)

[6] 索南加乐, 宋国兵, 邵文权, 等. 两端带并联电抗器输电线路永久故障判别[J]. 电力系统自动化, 2007,31(20): 56-60.

SUONAN Jia-le, SONG Guo-bing, SHAO Wen-quan,etal. Identification of permanent faults based on differential current protection for transmission lines with two shunt reactors [J]. Automation of Electric Power Systems, 2007, 31(20): 56-60. (In Chinese)

[7] 林达，王慧芳，何奔腾，等. 基于波形相关性的带并联电抗器线路永久性故障判别方法[J]. 电力系统自动化,2013，37(16)：80-85.

LIN Da，WANG Hui-fang，HE Ben-teng，etal. Identification of permanent fault at transmission lines with shunt reactors based on waveform correlation [J]. Automation of Electric Power Systems，2013，37(16)：80-85. (In Chinese)

[8] 田 野，周念成，赵 渊，等. 基于故障相电压功率谱的高压输电线路单相自适应重合闸[J]. 电网技术，2008，32(16)：22-26.

TIAN Ye，ZHOU Nian-cheng，ZHAO Yuan，etal. Single-phase adaptive reclosure for EHV/UHV transmission line based on power spectrum of faulty phase voltage [J]. Power System Technology，2008，32(16)：22-26. (In Chinese)

[9] 梁振锋，索南加乐，康小宁，等. 利用自由振荡频率识别的三相重合闸永久性故障判别[J]. 中国电机工程学报，2013，33(7)：124-131.

LIANG Zhen-feng, SUONAN Jia-le, KANG Xiao-ning,etal. Permanent faults identification using free oscillation frequency for three-phase reclosure on transmission lines with shunt reactors [J]. Proceedings of the CSEE，2013，33(7)：124-131. (In Chinese)

[10]SAUL G B, WILLIAM F H. A computer model of the secondary arc in single phase operation of transmission lines [J]. IEEE Trans on Power Delivery, 1989, 4(1): 586-595.

[11]JONATHAN S SMITH．The local mean decomposition and its application to EEG perception data [J]．Journal of the Royal Society Interface, 2005, 2(5): 443-454.

[12]PINCUS S M．Approximate entropy as a measure of system complexity [J]．Proceeding of the National Academy Sciences USA，1991，88(6)：2297-2301.

[13]邓乃杨，田英杰. 支持向量机：理论、算法与拓展[M]. 北京：科学出版社，2009.

DENG Nai-yang, TIAN Ying-jie. Support vector machine: Theory, algorithms and expand [M]. Beijing: Science Press, 2009. (In Chinese)

[14]吴文辉，曹祥麟. 电力系统电磁暂态计算与EMTP应用[M]. 北京：中国水利水电出版社，2012.

WU Wen-hui, CAO Xiang-lin. Power system electromagnetic transient calculation and application of EMTP [M]. Beijing: China Water Power Press, 2012. (In Chinese)

Adaptive Reclosure Method Based on LMD-approximate Entropy and SVM

JIANG Ya-qun†,LENG Chong-fu,HUANG Chun,DAI Xu-sheng

(College of Electrical and Information Engineering, Hunan Univ, Changsha, Hunan 410082,China)

The key function of adaptive reclosing is to correctly identify fault nature and quickly capture the transient fault arc extinction time. Based on the analysis of the waveform complexity of fault terminal voltage after circuit breaker tripping under transient fault and permanent fault, this paper presented an adaptive reclosing overall implementation by combining local mean decomposition (LMD), approximate entropy and support vector machine (SVM). After getting the PF components of fault signal by using LMD decomposition, the approximate entropy of the first three PF components is calculated, which constitutes a three-dimensional feature vector as the input of SVM to identify fault nature and to capture arc extinguishing moment. Simulation results verify that this method can intelligently distinguish the transient fault from permanent fault, and capture transient fault extinction time with a strong anti-noise ability.

adaptive reclosure; local mean decomposition; approximate entropy; support vector machine

1674-2974(2015)08-0074-07

2014-06-28

国家电网公司研究项目(5216A313500N)；国家863高技术基金资助项目(2012AA050215)

江亚群(1971-)，女，湖南桃源人，博士后，湖南大学副教授

†通讯联系人，E-mail:yaqunjiang@21cn.com

TM76

A