基于定位装置参数等效的接触网二维力学模型

关金发,吴积钦

(西南交通大学电气工程学院, 成都　610031)



基于定位装置参数等效的接触网二维力学模型

关金发,吴积钦

(西南交通大学电气工程学院, 成都610031)

摘要：接触网既是供电的线路,又是受电弓的滑道,其结构为三维柔性索网,当受电弓通过时,支持点和张力补偿点不存在瞬时大位移,其动态行为可以忽略,定位点由于存在非线性铰接,定位点处的动态行为不能被忽略。为等效定位点的动态行为,通过静力学分析,简化三维力学模型,将定位装置的三维非线性铰接等效为二维线性弹簧,并推导弹簧的等效刚度值计算公式,得到接触网二维力学模型。最后通过仿真实例,验证接触网二维力学模型的静态和动态效果与接触网三维模型完全吻合,并确认定位装置等效刚度的计算方法。

关键词：接触网；力学模型；定位装置

接触网由若干锚段组成，每一锚段的接触网可看作一张柔性索网，而控制索网形状的主要点有若干承力索支持点、接触线定位点和张力补偿点，这3种控制点决定接触网是一个三维力学模型。

接触网三维力学模型中承力索支持点的受力直接传递给支持结构，支持结构为三角形结构，不存在大位移。张力补偿点通过转换柱上的定位点向支柱外拉出线索，但转换柱上的定位点是固定在定位管上的，也不存在大位移。接触线定位点不仅需确保受电弓通过时有合理的抬升量，还需尽可能利用受电弓滑板的工作范围，使受电弓滑板磨耗均匀，故其结构尤为重要。另外，除转换支柱外，定位点均通过定位器连接，定位器与定位支座或定位环之间的铰接属于非线性接触，存在大位移。在接触网力学计算中，三维力学模型虽然接近真实的接触网结构，但由于其结构的复杂且存在非线性接触，即使通过数值计算也很难得到收敛解，且耗费的求解时间较长。故有必要研究接触网的二维力学模型。

国内外弓网动力计算大都采用接触网二维力学模型。文献[1-3]在接触网静力计算时，定位装置的转动被忽略，定位装置可等效为一质量点，利用有限元法得到接触网的初始平衡位置。文献[4-5]虽然定位点也等效一质量点，但文中忽略接触网拉出值方向的几何参数，在求解弓网动态问题时，定位点不存在转动，与真实接触网结构相差较大。文献[6-12]均把定位装置等效为弹簧质量单元，质量为定位器质量的一半，文献[6-8]弹簧刚度值并未提及，文献[9-12]弹簧刚度均取130 N/m，但未给出等效弹簧刚度的相应计算方法，制约了接触网二维力学模型在工程应用中的使用。

为解决这一问题，通过静力学等效，简化三维力学模型，将定位装置的三维非线性铰接等效为二维线性弹簧，忽略张力补偿点的拉出转角，并假设支持点、定位点的转动只考虑沿线路中心线的纵向位移，支持点、定位点、张力补偿点处于同一平面，该平面垂直于轨面，得到接触网二维力学模型。

接触网二维力学模型在接触网静力计算和受电弓动力计算时只需考虑二维平面力学计算，模型简单，求解收敛容易，计算结果与三维模型非常接近，为接触网结构计算和结构优化提供一种新的方法。

1接触网定位装置静力计算

接触网有多种定位装置，按照不同的分类方式有：限位定位装置和非限位定位装置；隧道内定位装置和隧道外定位装置；弹簧定位装置和非弹簧定位装置等等。但这些装置的共同点都是通过铰接关节连接定位器，定位器通过定位线夹连接接触线，假设只考虑定位装置垂直平面的运动，把定位装置等效为图1物理模型，为一长度ld一端连接平面铰接关节一端连接接触线的直杆，铰接关节的另一端为固定端。

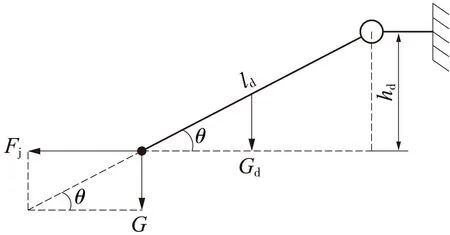
图1　接触网定位装置物理模型

图1中直杆的位置受拉出值分力Fj、接触线自重Gj和定位器自重Gd的影响，定位器高度hd由如下公式计算

(1)

式中hd——定位器高度，m；

Fj——由拉出值产生的水平拉向线路中心的张力分量，N;

ld——定位器长度，m；

G——定位点承受垂向重力，N，G=Gj+Gd/2，Gj为定位器悬挂接触线的重力，Gd为定位器自重。

假设定位器需承担共l长的接触线重力，定位器自重Gd沿ld均匀分布，式(1)改写成

(2)

式中gj——接触线单位长度重力，N/m；

gd——定位器单位长度重力，N/m。

Fj由两个拉向线路中心的分力组成，其计算公式为

(3)

式中a1、a2、a3——定位装置拉出值，m；

L1、L2——跨距，m；

Tj——接触线补偿张力，N。

2接触网静态形状计算

接触网定位装置等效刚度的计算与具体的接触网参数有关系，以典型的接触网形式作为分析对象，等效计算有以下几个前提条件：

(1)假设接触网沿直线区段布置，且接触网线索两端沿线路中线方向张力恒定；

(2)假设接触线、承力索由若干个直线杆单元组成，不考虑节点间的静态形状；

(3)假设接触线无预留弛度悬挂，且忽略吊弦及线夹自重。

不同的接触网参数，接触网的静态形状也不相同，为研究方法具有通用性，选择2个不同参数的跨距进行分析，如图2所示。图2中L1跨距内有n根吊弦，L2跨距有m根吊弦，定位点至第1吊弦点水平距离均为l1，吊弦间距按跨距减2倍l1之差均匀布置。为表示不同跨距的计算值，左边跨距均用大写字母表示，右边则用小写表示。

图2　接触网计算模型静态形状

通过前提条件已知，接触线无预留弛度且吊弦节点、定位点之间为一个直线杆单元，此时吊弦节点力F1～Fn与f1～fm的计算以fk为例，fk由两部分组成，分别为fk、1和fk、2，xk表示节点位置，其计算公式如下

(4)

由于计算接触网定位装置等效刚度时，需在定位点加一定的抬升力，此时，吊弦节点力将重新分布，接触网的静态形状必然改变，故需要计算接触网的静态形状，承力索是影响接触网的关键因素之一，下面将推导承力索的吊弦节点位置的计算公式。

由于静态平衡下抛物线单元节点处的力矩为0，故把悬挂点1和吊弦点1之间的承力索看作1个直线杆单元，计算吊弦节点1的力矩，见图3。

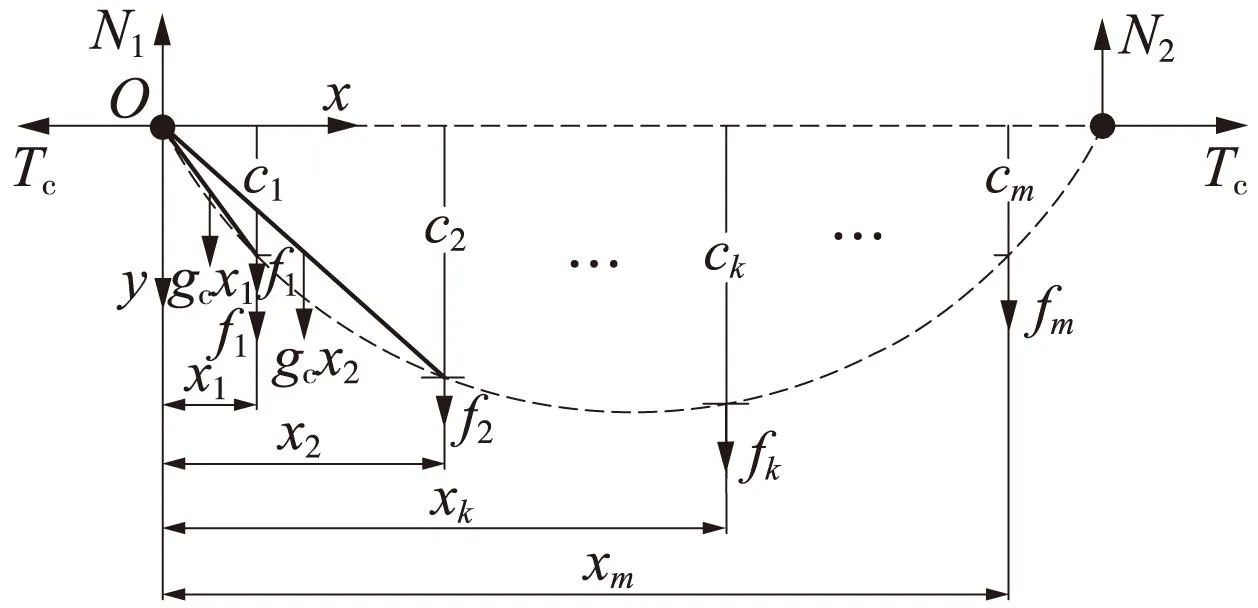
图3　承力索吊弦节点位置计算示意

(5)

得吊弦节点1的垂向位移

(6)

把悬挂点1和吊弦点i之间的承力索看作1个直线杆单元，计算吊弦节点i的力矩，见图4。

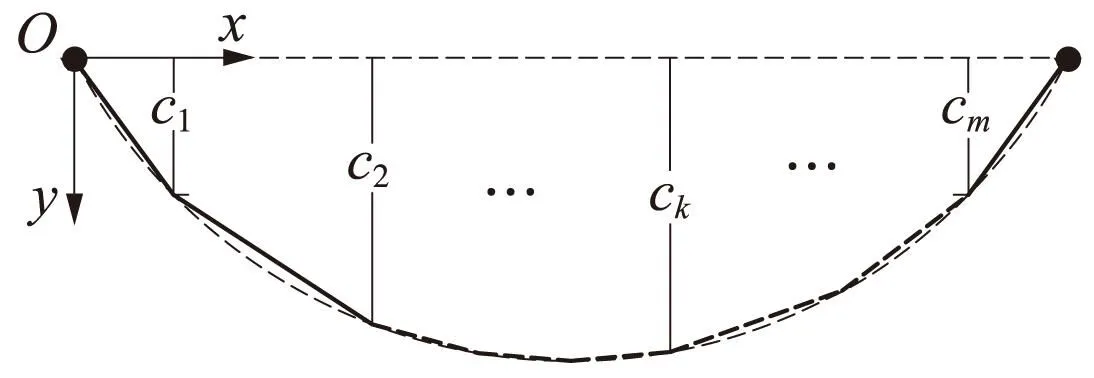
图4　承力索静态形状

(7)

得吊弦节点i的垂向位移

(8)

至此，承力索的每个吊弦节点坐标已求出，按照每两节点间一个直线杆单元，承力索静态形状如图4所示。此时的接触网为初始静态形状，即初态。

3接触网定位装置等效刚度计算

刚度是零件载荷与位移成正比的比例系数，即引起单位位移所需的力。考虑定位装置中接触线张力提供了拉向线路的作用力，故其计算不能套用接触网弹性计算公式，设定位装置的等效刚度为

(9)

式中kd——定位装置等效刚度，N/m；

fup——引起定位装置抬升的分力，N；

hup——定位装置的抬升量，m。

当一定的抬升力作用于定位装置时，定位装置产生一定的抬升量hup，设抬升力为Fup，按标准EN50367[13]中第7.2条款典型接触力范围，若考虑Fup超出5%接触力范围即为小概率事件，Fup落在95%的接触力范围，即0.4Fm～1.6Fm，按照7.2条中平均接触力目标值曲线，速度取350 km/h时，Fup取值为75～302 N。以接触线截面150 mm2，第1吊弦离定位点为5 m，第1吊弦至第2吊弦间距为9 m，吊线对称布置为例，计算定位点附近吊弦的吊弦节点力Fn-1、Fn、f1、f2之和为370 N，故加载抬升力Fup，只对Fn-1、Fn、f1、f2、G五个力有影响，不影响其他吊弦节点力，即其他吊弦节点力与初始静态平衡大小一致。

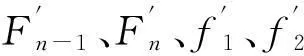
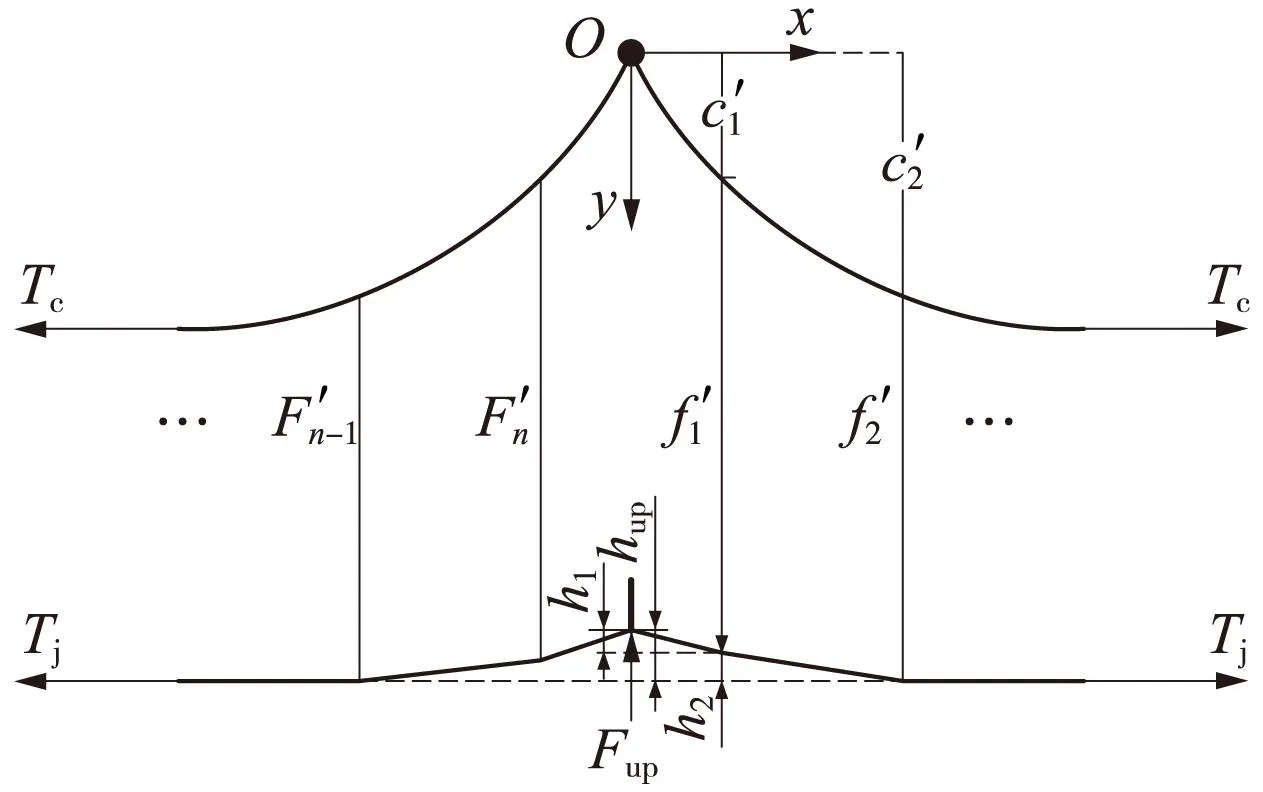
图5　定位点受抬升力作用后接触网静态形状

先计算抬升力Fup作用后引起L2跨距的力和几何改变，其接触线受力见图6。由第2节假设可知，接触线为无预留弛度悬挂，即承力索吊弦节点的位移改变与接触线吊弦节点的位移改变相等，如图6中Δc1、Δc2,其值为

(10)

式中ck——初始状态承力索吊弦节点垂向位移，m；

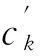
(11)

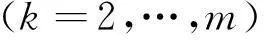
(12)

抬升力Fup改变吊弦节点力f2的前提是吊弦节点力f1=0，即上述方程存在条件

(13)

(14)

当f1>0，即第1吊弦拉紧，此时，除第1吊弦以外的吊弦节点力不变。

当f1=0，即第1吊弦松弛，此时，可以把第1吊弦删除，原有第2吊弦当作第1吊弦分析。

图6　L2跨距内接触线受力示意

3.1定位点抬升力使第1吊弦拉紧时定位装置等效刚度计算

将式(13)代入式(11)、式(12)中，得到第1吊弦拉紧时的吊弦节点抬升量

(15)

(16)

从图6知，定位点及各个吊弦节点由于存在不等高悬挂，直线杆单元的两悬挂点产生不相等的悬挂力，此不相等的悬挂力的大小取决于直线杆单元与水平面的夹角α、β，该夹角存在有如下关系

(17)

对L2跨距内接触线吊弦节点1列写力的平衡方程

(18)

以上分析方法针对L1跨距同样适用，改写式(15)、式(16)、式(18)，得

(19)

ΔCi=(Fn-F′n)(L1-Xn)XiL1Tc，(i=2，…，n)

(20)

(21)

由式(1)可知，定位装置的抬升高度与水平拉力、定位点承受垂向重力有关，此处虽然定位装置抬升了hup，定位装置受力仍满足式(1)，对新的定位点平衡位置受力分析，如图7所示，由于定位器长度不变，绕原点o旋转，从初始平衡位置a至新的平衡位置b，列写b点的力平衡方程

(22)

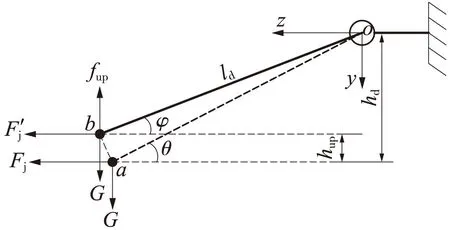
图7　定位点抬升后定位点受力示意

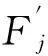
对图6中定位点受力分析，抬升力Fup须提供L2跨距内接触线P1大小的悬挂力。同理，对L1跨距内接触线受力分析，抬升力Fup须提供L1跨距内接触线Q1大小的悬挂力，如图8。故定位点抬升力Fup的计算公式为

(23)

图8　定位点所受合力示意

3.2定位点抬升力使第1吊弦松弛时定位装置等效刚度计算

将式(14)代入式(12)中，得到第1吊弦拉紧时的吊弦节点抬升量

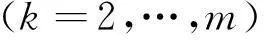
(24)

由于当Fn=f1=0，第1吊弦松弛，故Δc1、ΔCn与接触线吊弦节点1、n的抬升无关，进一步，此时图6中第2吊弦可当做第1吊弦，第1吊弦承受的接触线自重平均分配到定位点与第2吊弦上，改写式(17)～式(22)，得

(25)

(26)

(27)

(28)

(29)

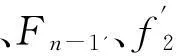
4二维力学模型验证

本节以EN50318提供的接触网模型作为研究对象，输入该参数，通过对比三维和二维动力学模型的接触网静态弹性和弓网动态性能，验证该计算方法的准确性。具体接触网参数见文献[14]，其接触网吊弦分布如图9所示。

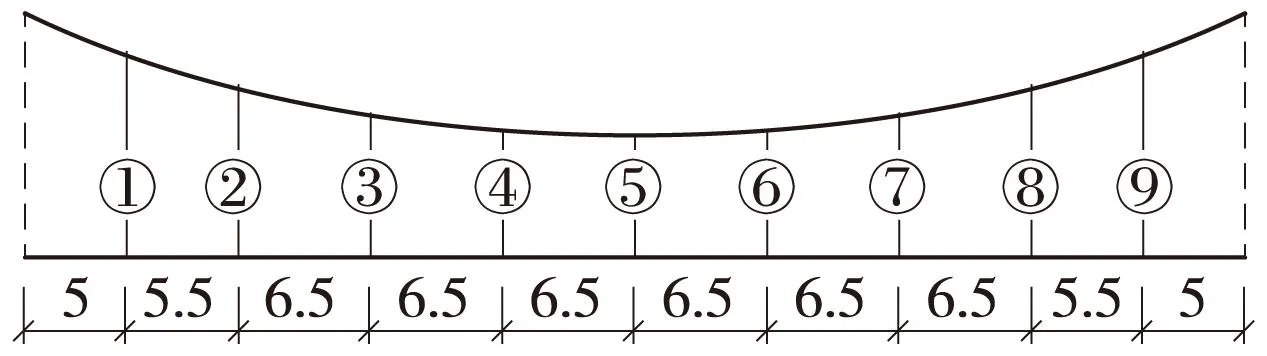
图9　接触网吊弦分布示意(单位：m)

首先按第2节给出的计算方法，计算该反映接触网初态的技术参数，结果见表1。

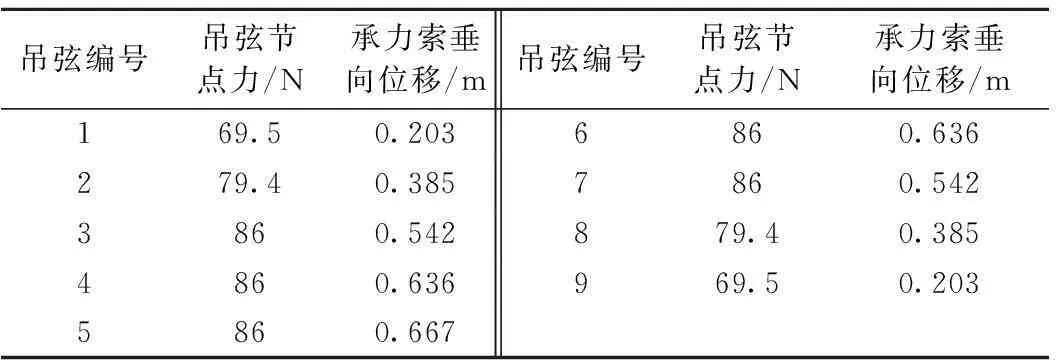
表1　接触网初态技术参数

注：接触线无预留弛度，吊弦点垂向位移为0；定位点水平拉力Fj=267 N，定位器初始高度hd=0.254 m

EN50318给出的受电弓静态压抬升力为120 N，忽略空气动力，故定位点抬升力Fup取48～192 N，将初态接触网参数代入式(15)～式(29)，计算该定位装置的等效刚度kd，结果见图10。

图10　定位点抬升力与定位装置等效刚度关系曲线

计算出定位装置等效刚度后，由于初始状态定位点须承担接触线部分重力和定位器重力之和G，故在考虑等效模型时，定位器有一半质量作为定位点处质点，弹簧单元需提供G大小的预拉力，带预拉力等效刚度弹簧单元见图11。图12能清楚的反映出两种接触网的空间布置。

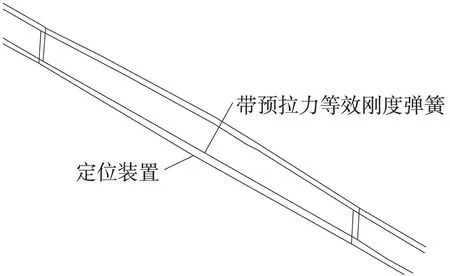
图11　三维模型与二维模型接触网立体示意

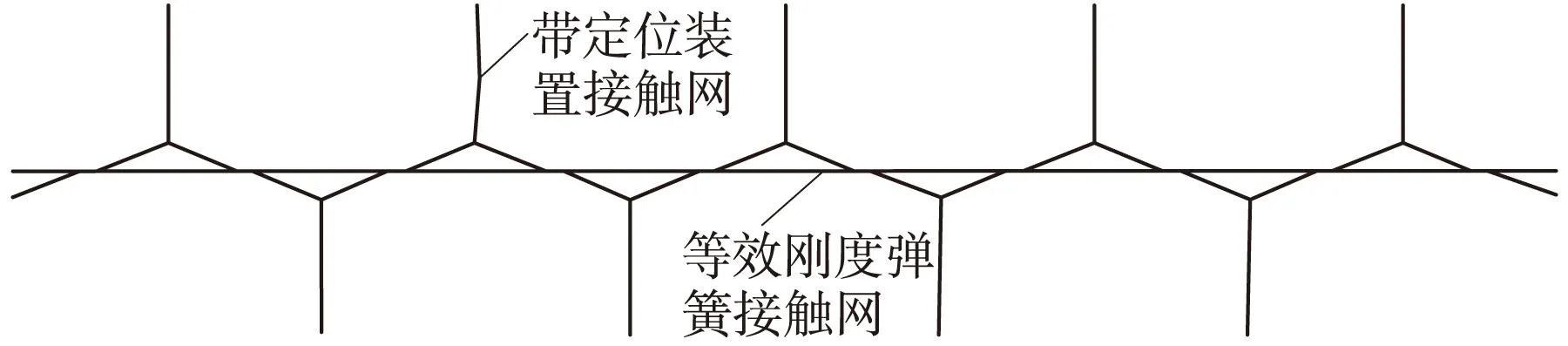
图12　接触网三维模型与二维模型平面示意

用静态接触接触压力70 N作为静态抬升力，分别计算两种接触网的静态弹性曲线，结果见图13。

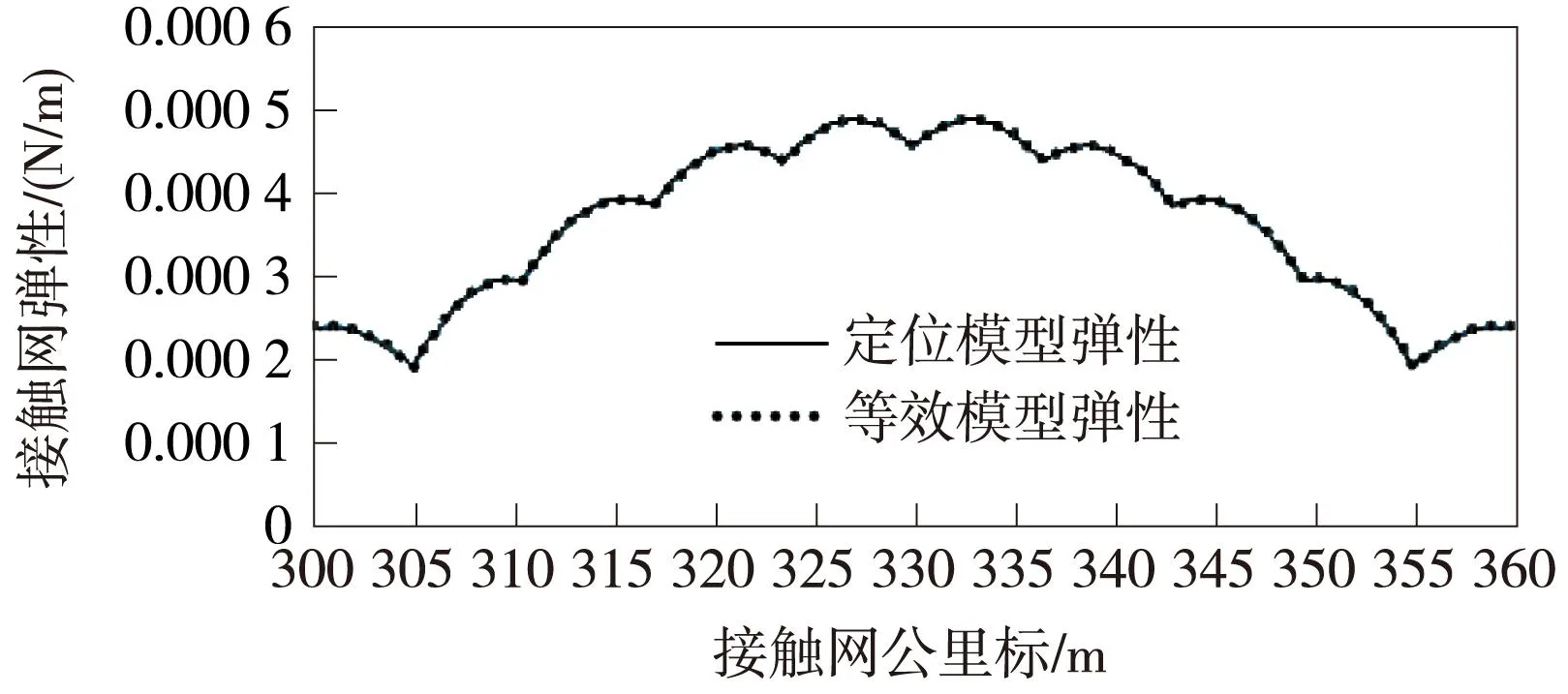
图13　定位模型与等效模型接触网静态弹性曲线

按照标准速度250 km/h、300 km/h分别仿真两种模型接触网，得到弓网动态互相作用参数，见表2，接触力结果见图14、图15，定位点抬升结果见图16、图17。

表2　弓网动态互相作用参数

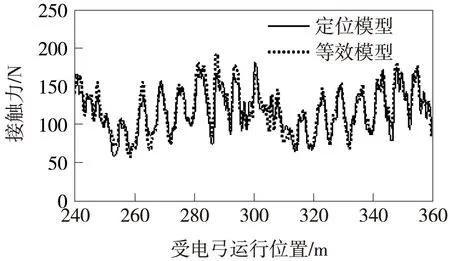
图14　250 km/h两种模型接触网分析区段接触力

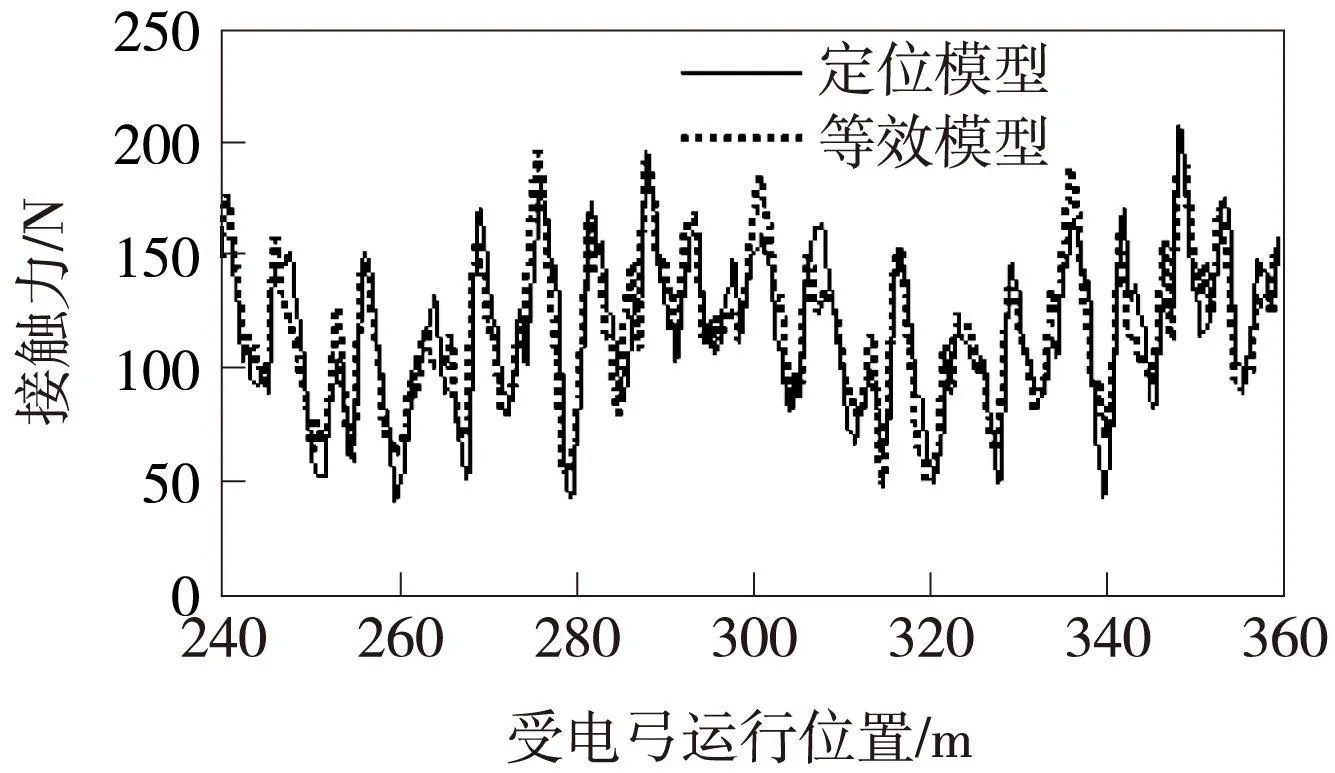
图15　300 km/h两种模型接触网分析区段接触力

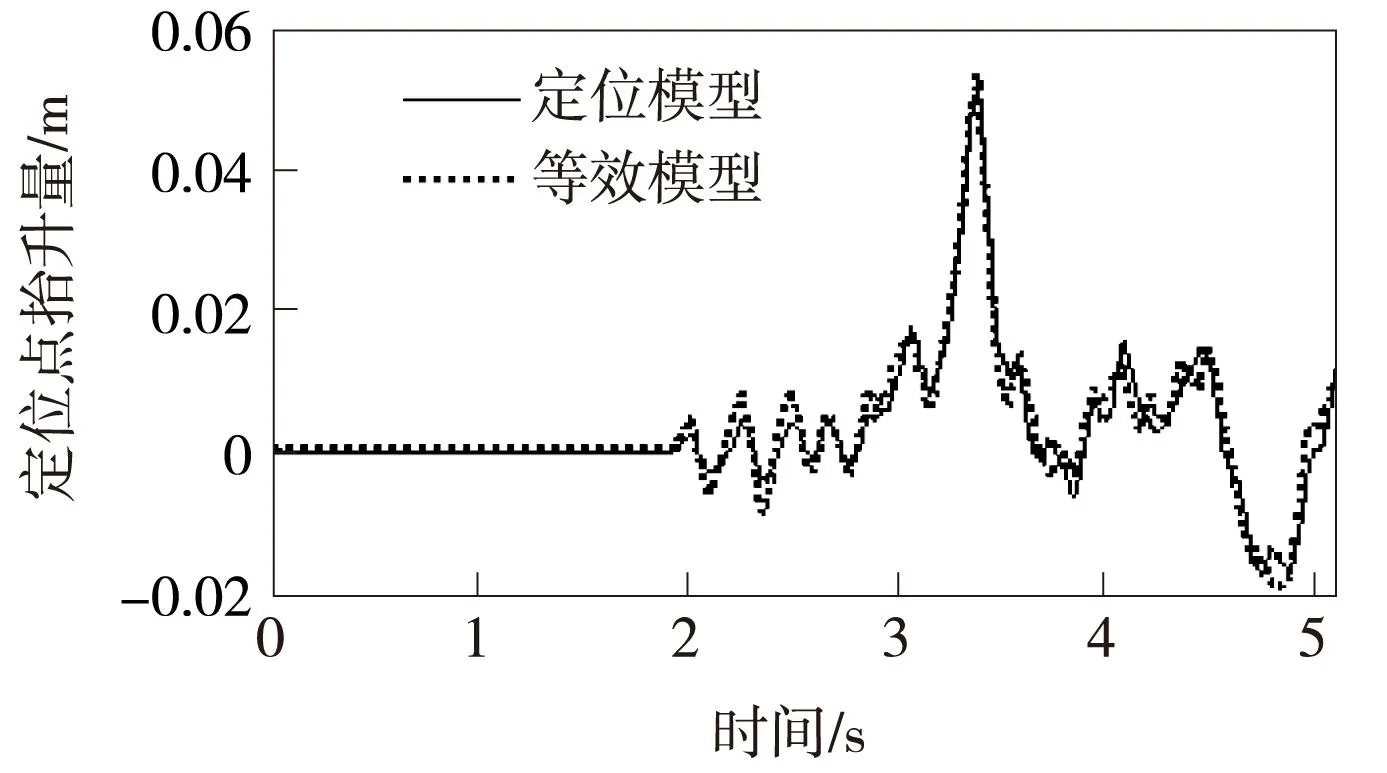
图16　250 km/h两种接触网分析区段定位点抬升量

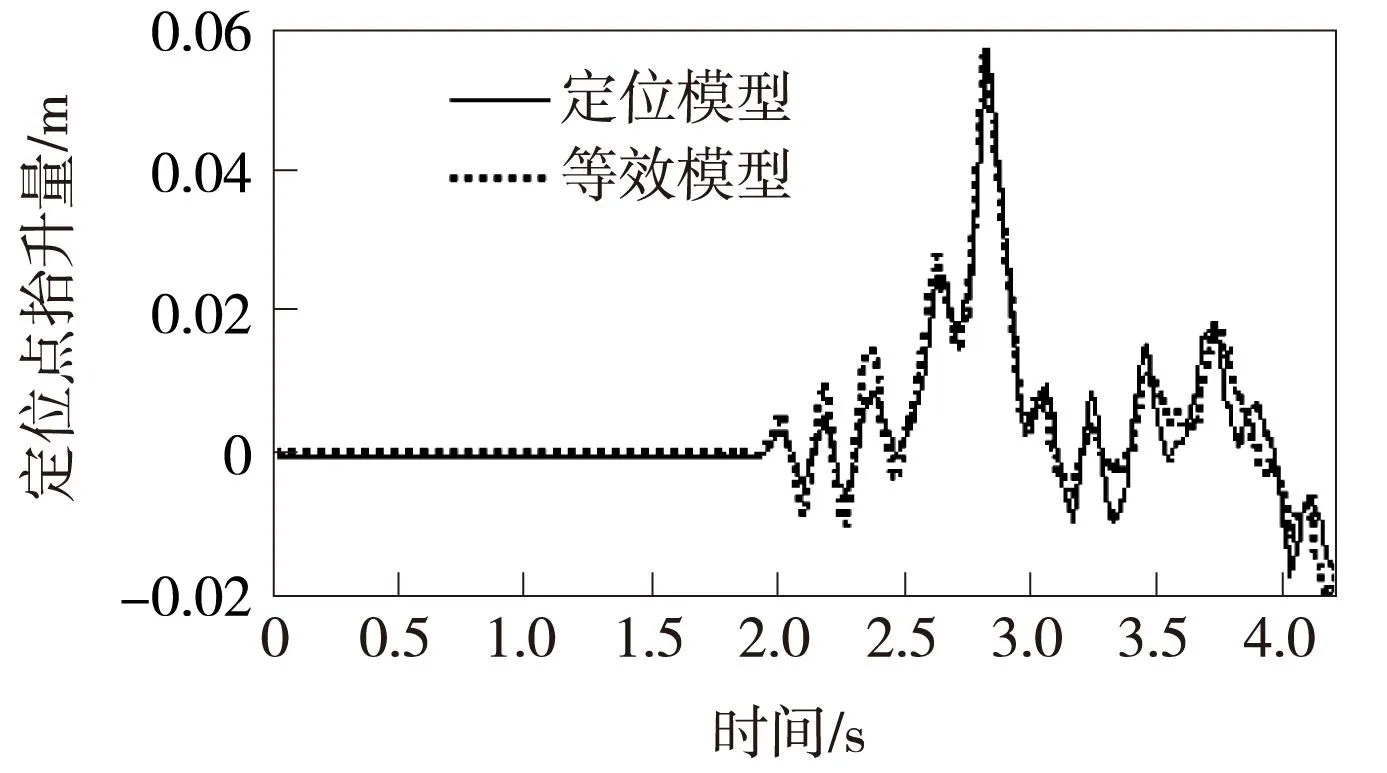
图17　300 km/h两种接触网分析区段定位点抬升量

从表2、图14～图17数据看，不同速度等级的三维力学模型与二维力学模型接触网的动态特性参数都相当接近，且都符合标准范围。接着利用相关系数分析250、300 km/h两种接触网的接触力、定位点抬升量数据的分布一致性，相关系数结果见表3。

表3　两种模型接触网动态特性参数相关系数

相关系数反映出两组数据的线性相关性，其绝对值越接近1，线性相关越强，从表3可知，各个相关系数都大于0.9，表明三维模型和二维模型的弓网动态参数具有很强的一致性。从分析结果可以得出，接触网二维力学模型可以等效接触网三维力学模型，同时验证定位装置等效刚度计算的准确性。

5结论

(1)对接触悬挂进行受力分析，推到接触网承力索的吊弦节点坐标计算公式，得到承力索的静态形状。

(2)当以一定的抬升力作用于定位装置时，分析两跨接触悬挂，以第1吊弦是否松弛为前提，分两种工况，进行静力学分析，得到定位装置的等效刚度计算方程组，代入抬升力和接触网参数求解该方程组，确定定位装置的平均等效刚度值。

(3)以EN 50318中标准模型进行三维和二维动力学分析，从静态和动态分析结果可以得出接触网二维力学模型可以等效接触网三维力学模型，同时验证定位装置等效刚度计算的准确性。

(4)接触网二维力学模型在曲线区段需要进行修正处理，有待进一步研究。

参考文献：

[1]李瑞平.初始平衡状态的接触网有限元模型[J].西南交通大学学报，2009，44(5)：732-737.

[2]Woonkyung M. Kim. A numerical study on dynamic characteristics of a catenary[J]. KSMS， 2003，17(6):860-869.

[3]阮杰.电气化高速铁路接触网静态模型的建立[J].铁道学报，2012，34(8)：20-25.

[4]周宁.350 km/h及以上弓网动态行为研究[D].成都：西南交通大学，2012.

[5]吴天行.弓网高速动态受流仿真研究[J].铁道学报，1996，18(4)：57-61.

[6]张卫华.接触网动态研究[J].铁道学报，1991，13(4)：26-33.

[7]Enrique Arias. A mathematical model of the static pantograph/catenary interaction[J]. International Journal of Computer Mathematics， 86：2， 333-340.

[8]于万聚.高速接触网-受电弓系统动态受流特性研究[J].铁道学报，1993，15(2)：16-27.

[9]刘怡.接触网动应力研究[D].成都：西南交通大学，2003.

[10]梅桂明.受电弓-接触网系统动力学[D].成都：西南交通大学，2010.

[11]蔡成标.高速铁路接触网振动特性分析[J].西南交通大学学报，1997，32(5)：497-500.

[12]W.M. ZHAI. Effect of Locomotive Vibrations on Pantograph-Catenary System Dynamics[J]. Vehicle System Dynamics， 29：S1， 47-58.

[13]EN50367：2006. Railway applications—Current collection system—Technical criteria for the interaction between pantograph and overhead line (to achieve free access) [S]. Brussels: CENELLEC， 2006.

[14]EN50318：2002. Railway applications—Current collection system—Validation of simulation of the dynamic interaction between pantograph and overhead contact line[S]. Brussels: CENELLEC， 2002.

欢迎订阅2015年《铁道标准设计》邮发代号 82-765刊号 CN11-2987/UISSN1004-2954

《铁道标准设计》创办于1957年，是中铁工程设计咨询集团有限公司主办的国内外公开发行的科学技术类期刊，铁路运输类中文核心期刊， 中国科技核心期刊。

■主要报道内容铁路及城市轨道交通线路、路基、轨道、桥涵、隧道与地下工程、机务、电力、电力牵引、通信、信号、给排水、站房建筑等专业的工程设计、科学研究；铁路工程建设标准规范的制修订、说明、勘误、更正以及新规范的宣贯；铁路、城市轨道交通等领域的最新动态等。

■读者对象铁路、城市轨道交通等部门从事相关专业的勘察设计、施工、制造、养护、科研等工作的技术、管理人员及相关专业的院校师生。

■ 《铁道标准设计》为A4开本，月刊。每月20日出版。每期定价20元，全年240元/份(含邮资)。

在线投稿：http:∥www.tdbs.cbpt.cnki.net/

E-mail:tdbsb@263.net

地址：北京市丰台区广安路15号中铁咨询大厦邮编：100055

电话：(010)5269630551830167/传真路电：(021)30167

《铁道标准设计》典型参考文献范例

1期刊论文——[J]

[1]汤晓光.无砟轨道客运专线沉降变形观测评估系统建设管理[J].铁道标准设计，2010(1)：3-6．

[2]王天亮，刘建坤，彭丽云，等.冻融循环作用下水泥改良土的力学性质研究[J].中国铁道科学，2010，31(6)：7-13．

[3]周丹，田红旗.强侧风下客车在不同路况运行的气动性能比较[J].中南大学学报：自然科学版，2008，39(3)：554-559.

2普通图书、专著—[M]

[1]郑健.中国高速铁路桥梁[M].北京：高等教育出版社，2008．

[2]龚晓南.地基处理手册[M].2版.北京：中国建筑工业出版社，2000．

[3]布列耶夫，克拉夫错夫.轨道电路的分析与综合[M].孙铭甫，译.北京：中国铁道出版社，1981:55-56．

3论文集、会议论文—[C]

[1]王梦恕，骆建军.客运专线长大隧道设计施工的讨论[C]∥铁路客运专线建设技术交流会论文集.武汉：长江出版社，2005:186-195.

[2]张忠智.科技书刊的总编(主编)的角色要求[C]//中国科学技术期刊编辑部学会建会十周年学术研讨会论文汇编.北京：中国科学技术期刊编辑学会学术委员会，1997:33-34.

4学位论文—[D]

[1]李小珍.高速铁路列车—桥梁系统耦合振动理论及应用研究[D].成都：西南交通大学，2000．

5标准、规范—[S]

[1]中华人民共和国铁道部.铁建设[2007]47号新建时速300～350公里客运专线铁路设计暂行规定[S].北京：中国铁道出版社，2007．

[2]铁道第二勘察设计院.TB10003—2005 铁路隧道设计规范[S].北京：中国铁道出版社，2005．

6科研报告—[R]

[1]中铁第四勘察设计院集团有限公司.武广铁路客运专线大跨度预应力混凝土连续梁桥技术研究总报告[R].武汉：中铁第四勘察设计院集团有限公司，2008．

7专利—[P]

[1]闫友联， 沈良成， 金仓，等.一种大跨度悬索桥施工中的先导索水面牵引的放索装置: 中国， 200920034476.1 [P]. 2010-05-05．

[2]闫友联， 沈良成， 金仓，等.一种大跨度悬索桥施工中的先导索水面牵引的放索装置: 中国， 200920034476.1[P]. 2010-05-05．

8电子文献(包括专著或连续出版物中析出的电子文献)[ M/OL] [J/OL]等

[1]江向东. 互联网环境下的信息处理与图书管理系统解决方案 [J/OL].情报学报，1999，18(2)：4[2000-01-18].http://www.chinainfo.gov.cn/periodical/qbxb/qbxb99/qbxb990203.

9报纸中析出的文献—[N]

[1]丁文祥. 数字革命与竞争国际化 [N].中国青年报，2000-11-20(15)．

10未说明文献类型或资料类—[Z]

[1]中华人民共和国铁道部.铁路GSM-R数字移动通信系统网络技术规划[Z].北京：中华人民共和国铁道部，2005．

Two-dimensional Mechanical Model of the Catenary Based on Equivalent Steady Device Parameters Guan Jin-fa, Wu Ji-qin

(Department of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Abstract：The catenary serves for power supply and as a path for pantograph sliding, When a pantograph is passing by, there is no large instant displacement at the support points and the tension compensation points, therefore the dynamic behavior can be ignored on account of its three-dimensional soft wire structure. However, the dynamic behavior at the fixing points cannot be ignored because of the non-linear hinge. To obtain the equivalent dynamic behavior of the fixing points, the three-dimensional mechanical model is simplified by static analysis, which converts the three-dimensional nonlinear hinge into a two-dimensional linear spring, and then the formula to calculate equivalent stiffness of the spring is derived and the two-dimensional mechanical model of the catenary is established. Finally, the static and dynamic effects of the two-dimensional mechanical model of the catenary are proved with simulation in full agreement with that of the three-dimensional mechanical model of the catenary, and the method to calculate the equivalent stiffness of the steady device is confirmed.

Key words：Catenary; Mechanical model; Steady device

中图分类号：U225

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2015.02.031

文章编号：1004-2954(2015)02-0128-06

作者简介：关金发(1986—)，男，博士研究生， E-mail：kwanjinfa@163.com。

基金项目：国家科技支撑计划(2011BAG01B04)

收稿日期：2014-04-11； 修回日期：2014-05-25