圆分布的平均角及其区间估计方法在传染病发病高峰评估中的应用探讨*

江苏省疾病预防控制中心（210009） 戴启刚

圆分布的平均角及其区间估计方法在传染病发病高峰评估中的应用探讨*

江苏省疾病预防控制中心（210009） 戴启刚

目的探讨圆分布在传染病发病高峰研究中的应用策略。方法以四类传染病数据为基础，圆分布方法分析各病种流行规律，采用两种区间估计方法计算发病高峰期。结果圆分布方法适用于单峰分布或略呈现双峰分布的传染病，对于双峰分布传染病，圆分布的雷氏检验并不能给出合理的结果；采用bootstrap计算发病高峰期区间过窄，标准差法结果较为合理。结论利用圆分布方法研究传染病的流行规律时，应当先作折线图以便对该病种流行规律有宏观了解，流行高峰应当结合折线图和雷氏检验结果观察，对传染病发病高峰期的计算，采用加减标准差法比bootstrap法更具优势。

传染病 圆分布 可信区间 bootstrap

圆分布分析适用于在规定时期内周期性变化的数据，检验数据在一个周期内是均匀分布的，还是有集中的倾向，如果有集中于某个时间发生的倾向，则可以通过平均角来表示［1］。近年来，有较多的研究将圆分布方法引入到传染病发病时间的规律分析中，以探索传染病的发病高峰和流行期［2-5］。本文以不同流行特征的传染病数据为基础，探讨圆分布的适用情况，比较两种发病高峰期计算方法（加减标准差法和bootstrap法）的合理性。

资料与方法

1.资料来源

为探讨圆分布在传染病发病高峰中的适用情况，本文选取几种不同类型的流行特征传染病：细菌性痢疾（单峰分布）、手足口病（双峰分布，两峰值水平相差较多）、水痘（双峰分布，两峰值水平相近）、丙型肝炎（均匀分布）。发病资料来源于中国疾控中心传染病报告信息管理系统。

2.资料整理

从传染病报告信息管理系统中导出江苏省2012年目标传染病报告卡，整理该传染病的每日发病数。

3.分析方法

（1）采用圆分布方法，求得该病种的发病高峰日。

采用雷氏检验（Rayleigh′s test）判断平均角有无统计学意义，以确认该传染病总体分布是否有集中于该高峰日的倾向。

（2）分别采用加减标准差法［5］和bootstrap法［6］估计发病高峰日的可信区间。

加减标准差法：将角度转化为日期，即为发病高峰期。

Bootstrap法：从现有的传染病发病数据中，等比例、有放回地重复抽样［7］（考虑到计算结果的稳定性和计算机运算效率，将抽样次数定为1000），计算每一个抽样样本的平均角，取1000个平均角的Q2.5和Q97.5作为95%可信区间的上下限［8］，并将其转化为相应的日期作为发病高峰期。

（3）评价方法

本文目标将传染病按日作发病数折线图，以全年日均发病数为界值，当某段时期日发病数超出全年日均发病数且整体发病趋势持续向上时，则初步判断该传染病发病可能进入高发，并试通过圆分布的统计量结合上述直观的方式，探讨圆分布方法以及两种区间估计方法的的适用情况。

本文数据整理与分析借助SAS 9.2完成，作图采用Office 2010软件。

结 果

通过目标传染病的日发病情况折线图，以日均发病数为辅助线，判断传染病进入高峰的时间（仅作为辅助判断，不作为判定依据）。见图1。

对四类传染病的圆分布分析及两种可信区间估计结果见表1。

丙型肝炎发病无季节性，全年发病呈均匀分布，此时利用雷氏检验可以较敏感地得到圆分布平均角无统计学意义的结论；水痘发病在一个自然年内，呈明显的双峰分布，但采用雷氏检验得到P值有意义的结论（下文将进一步探讨）；手足口病在夏季出现高峰后下行，至年末又出现流行小高峰，平均角所对应的高峰日与实际情况较为吻合，经雷氏检验有统计学意义；细菌性痢疾是夏秋季节高发的肠道传染病，呈严格的单峰分布，平均角所对应的发病高峰日符合实际发病情况。

传染病发病高峰期的计算，本文分别采用了非参数bootstrap再抽样百分位数法和加减标准差法，结合发病折线图显示bootstrap的方法得到的可信区间过窄，无实际意义，而加减标准差法得到的结果较为客观：手足口病和细菌性痢疾作为肠道传染病，其发病具有明显的季节特征，发病数一般随着气候转暖（3月份左右）而升高，4月至7月为发病高峰期［9］。这与本文所得到的的结果一致，因此采用圆分布法时，利用加减标准差法估计发病高峰期更具有流行病学的指导意义。

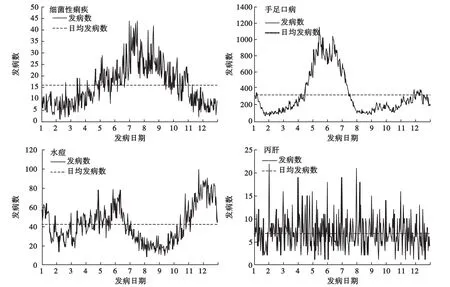
图1 四类传染病日发病折线图

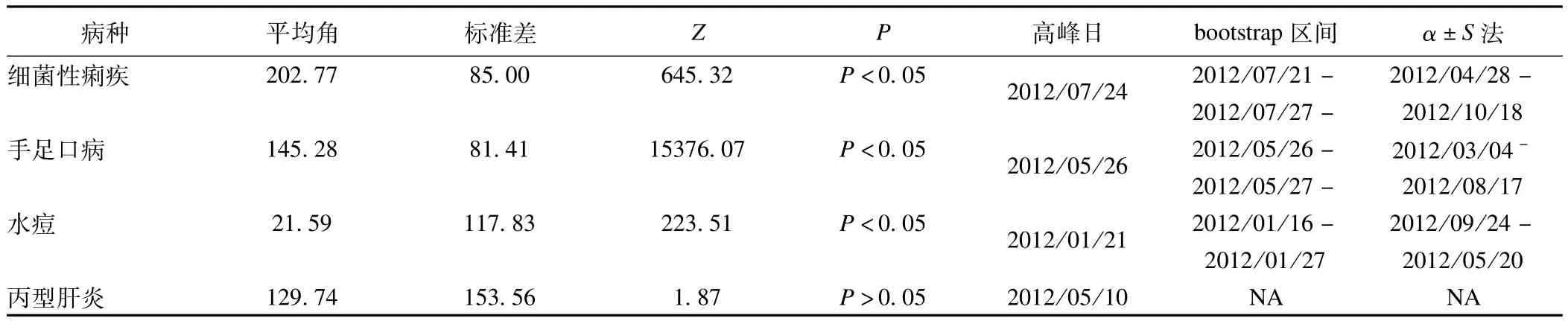
表1 四类传染病圆分布分析及发病高峰期结果

上文讨论了圆分布方法在四种传染病发病集中性以及发病高峰期中的应用，其中对水痘的平均角检验具有统计学意义，然而从发病折线图看，呈典型双峰分布，观察加减标准差法得到的高峰期可见，该传染病的发病高峰期跨越了一个自然年，考虑到该现象可能是由于2011年下半年的发病高峰与2012年上半年的发病高峰相延续而产生，结合表1中的结果，尝试以2011／08／01-2012／07／31作为一个观察周期，重新计算平均角及其对应高峰期（采用加减标准差法），计算得到发病高峰日为2012／02／15，雷氏检验P＜0.05，高峰期为2011／10／16-2012／6／17，结合发病折线图（图2）可知在该周期内该传染病仍呈双峰分布，且计算所得的发病高峰与实际发病情况不符，发病高峰出现跨年度的现象并非上文所假设的原因。

讨 论

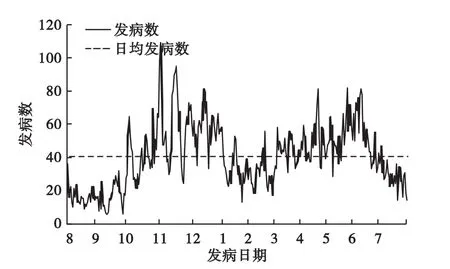
图2 水痘2011／08／01-2012／07／31日发病折线图

圆分布方法被广泛应用于传染病发病高峰期的计算和比较，本文通过对四种不同流行特征的传染病的研究证实：圆分布方法适用于单峰分布传染病（如细菌性痢疾）或略呈现双峰分布的传染病（手足口病）；若发病趋势平稳（如丙型肝炎），雷氏检验能够得到无集中时点发病的结论；而对于一个观察周期出现两个发病高峰且两高峰水平相当的传染病（如水痘），圆分布的雷氏检验并不能给出合理的结果。因此，本文建议，利用圆分布方法计算某传染病的发病高峰、比较不同观察周期和（或）不同类型传染病发病高峰时，应当遵循如下步骤：（1）初步用折线图观察传染病的发病趋势；（2）利用圆分布方法分析，采用雷氏检验分析是否存在平均角；（3）将雷氏检验统计量与发病折线图相结合，给出相关结论。

对于传染病高峰期的计算，因为传染病年发病例数较多，若采用非参数bootstrap抽样的百分位数法，计算耗时且得到的可信区间较窄，本文建议使用将转化为日期的方法，可以简便、可靠地得到具有流行病学意义的结果。

1.金丕焕，陈峰主编.医用统计方法（第3版）.上海：复旦大学出版社，2009：327-334.

2.石长胜，邵峰，王笃宝.应用圆形分布分析泰安市不同时期麻疹发病的时间分布特征.中国卫生统计，2006，23（2）：155-156.

3.徐红梅，朱渭萍，费怡，等.应用圆形分布法分析浦东新区2005-2010年细菌性痢疾季节性分布特征.中华疾病控制杂志，2012，16（5）：446-448.

4.甘仰本，廖征.集中度和圆形分布法分析南昌市1985-2007年麻疹季节性分布.现代预防医学，2009，36（12）：2229-2230.

5.聂轶飞.应用集中度和圆形分布法探讨河南省2010年手足口病流行规律.中国卫生统计，2013，30（3）：410-411.

6.朱凯.圆形分布资料平均角置信区间的Bootstrap方法实现.中国卫生统计，2011，28（4）：412-413.

7.闫宇翔.Bootstrap再抽样方法的SAS程序设计.中国卫生统计，2003，20（5）：320.

8.Carpenter J，Bithell J.Bootstrap confidence intervals：when，which，what？A practicalguide for medical statisticians.Statisticsin Medicine，2000，19：1141-64.

9.嵇红，李亮，吴斌，等.江苏省2008至2010年手足口病流行病学及病原学特征分析.中华儿科杂志，2012，50（4）：261-266.

（责任编辑：丁海龙）

江苏省“十二·五”科教兴卫工程（ZX201109）