模糊聚类法在动态设计组学数据趋势聚类中的应用*

山东大学公共卫生学院生物统计学系（250012） 王 璐 张 涛 刘 佳 刘盈君 公晓云 薛付忠

模糊聚类法在动态设计组学数据趋势聚类中的应用*

山东大学公共卫生学院生物统计学系（250012） 王 璐 张 涛 刘 佳 刘盈君 公晓云 薛付忠△

目的探讨模糊C均值聚类方法（FCM）在动态设计组学数据不同动态趋势聚类中的应用。方法使用模糊C均值聚类方法，分别对模拟的动态数据和动态基因表达进行聚类，识别不同的变化模式。结果对模拟数据的分析显示，FCM可以准确地识别模拟设定的不同动态变化趋势，并将其聚为一类；同时，通过设定隶属度阈值我们可以避免对噪声变量的聚类。而对动态基因组表达数据的实例分析表明FCM可以有效地将具有相同表达模式的基因聚类，并且能给出类间关系。结论模糊C-均值聚类可以用于动态组学数据不同动态变化模式的聚类，帮助我们更有效地探索生物信息。

动态组学数据 模糊C均值聚类

生命过程是动态连续的，且存在一定的趋势和规律。传统的组学研究多为基于静态采样设计的分类研究，很难追踪生物体的纵向变化趋势。而动态组学研究设计是指在一个连续时间段内的多个时间点上对生物样本进行采样并测量的设计类型［1］。它使得分析生物体在疾病或外界干预刺激下的动态变化规律变为可能。相比于静态采样，动态采样使得我们可以测量和控制不同类型的变异，例如代谢动力学的个体差异，生理节奏，以及响应快慢的差异等，从而帮助我们更准确地找到随时间变化的关键标记物。例如，通过测量酵母菌细胞周期不同时间点的基因组表达水平，我们可以识别同酵母菌细胞周期相关的关键基因并了解其变化规律，从而为我们理解细胞周期的调控过程提供新的线索。

近年来，动态设计的组学研究逐渐成为热点。而如何识别动态设计组学数据中随时间变化的关键生物标记物及其变化趋势，是统计分析的关键。动态设计组学数据除具有纵向数据的特点外，还具有一般组学数据的高维、小样本特性，并且其中存在许多变化趋势相似的变量以及不随时间变化的噪声变量。利用单变量统计分析，例如重复测量方差分析，我们可以识别随时间变化的标记物，但是无法识别其复杂的变化趋势，且忽略了变量间的相关性。而使用无监督的聚类分析，能够同时考察所有变量，将其中变化趋势一致的生物标记物识别出来，这对于生物机制的研究具有重要意义。模糊聚类允许将聚类对象模糊归类，即使其以不同的隶属度属于不同的类，避免了随机化变量的归类，因而对噪声更加稳健［2］，适合于分析存在着大量噪声的组学数据。同时该算法允许类间重叠，并给出各个类之间的关系，因此能帮助我们更有效地挖掘生物样本数据中蕴含的复杂的生物网络调控信息。目前模糊C均值聚类算法已经被应用于组学数据的聚类分析中［3-5］。

本文在简要介绍模糊C均值聚类原理的基础上，通过对模拟数据和实际数据的分析介绍其在动态组学数据中的应用，考核其识别不同变化趋势的效果。

原理和方法

模糊C均值算法（fuzzy C-means clustering，FCM）是通过计算隶属度来确定每个数据点属于各个类的程度的一种聚类算法。该算法于1973年由Bezdek［6］提出，作为早期硬C均值聚类（HCM）方法的一种改进。

FCM的核心思想为：按照隶属度模糊划分，将n个向量xi（i＝1，2，…，n）分为c个模糊组，并求每组的聚类中心，使目标函数达到最小。模糊C均值算法与K均值聚类相似，主要区别在于FCM使用模糊划分，对于每个数据点用取值在（0，1）间的隶属度来确定其属于各个组的程度。隶属矩阵U中的元素uij取值在0到1之间，表示个体xj隶属于组i的程度，并且满足每个给定数据点xj的隶属度和等于1：

FCM的目标函数为：

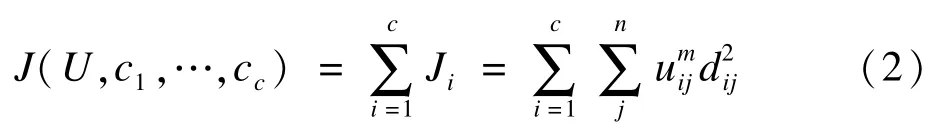
上式中dj＝‖xj－cj‖为样本xj到模糊组i聚类中心vi的欧氏距离；m为模糊参数，满足m∈［1，∞）。推导使目标函数最小化的条件，可以得到更新质心的计算公式：

和更新隶属度矩阵的计算公式

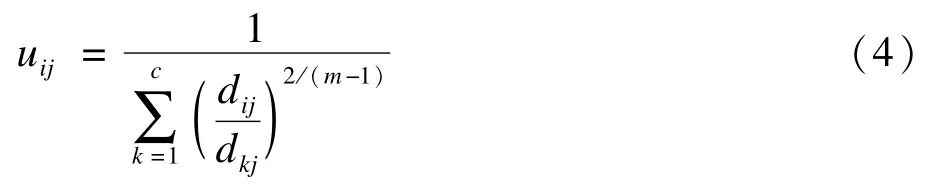
FCM算法过程如下：

（1）初始化隶属矩阵U，使其满足式（1）中的约束条件；

（2）使用（3）式，计算每个聚类的质心ci，i＝1，…，c。

（3）根据新的质心，使用（4）式更新隶属度矩阵U。

（4）计算目标函数。如果它小于某个确定的阈值，或它相对上次目标函数值的改变量小于某个阈值，则算法停止。否则返回步骤（2）。

上述算法也可以先初始化聚类中心，再进行迭代。FCM算法不能确保算法收敛于最优解，其性能依赖于聚类中心的初始位置。同时，算法需要预先设定聚类数目c和模糊系数m。对于c的设定，我们可以借助多种非监督簇评估度量来近似确定正确的聚类个数。m是决定模糊聚类性能的重要参数，随着m值增大，划分会变得越来越模糊，则聚类效果越差；而如果m过小，聚类结果则会接近于硬聚类，当m＝1时，聚类将完全退化为硬聚类。对于如何更好地确定初始聚类中心，及合适的聚类个数和模糊系数，一直是研究的重点和难题。

FCM算法的输出为c个聚类中心点向量，和一个c×n的隶属度矩阵。聚类中心表示的是每个类的平均特征，可以认为是该类的代表点。隶属度矩阵中包含每个样本属于各个类的隶属度，我们可以按照最大隶属原则或通过设置隶属度阈值确定每个样本点的归类。

目前FCM方法已经广泛应用于多个领域，有简便的实现方法，例如MATLAB软件中的FCM命令，R软件中用于基因组数据聚类分析的M fuzz包［7］。本文将使用R中的M fuzz包进行分析。

模拟实验

1.模拟数据设置。为考察模糊C均值聚类能否将具有不同变化趋势的变量分别聚类，我们设置了5种变化趋势的变量。设t表示时间点，为取值［1，12］间的整数，e服从标准正态分布，5种变量随时间变化的模型如下：

①单调递增y＝t＋e

②单调递减y＝-t＋e

③先减后增y＝β×cos（w×t）＋e

④先增后减y＝-β×cos（w×t）＋e

⑤周期波动y＝-β×cos（2×w×t）＋e

设置其中β＝3，w＝2π／12，每个变量都包含有12个时间点的数据，而每种趋势的变量个数为30个。同时设置500个服从标准正态分布的噪声变量，共650个变量。最后将数据标准化，使其每个变量均值为0，标准差为1。

2.模糊C均值聚类法分析过程

（1）模糊参数的选择

m的设置既要防止噪声变量被归类，又要避免分类过于模糊从而使聚类效果变差。根据这一原则，可以使用文献［8］提供的简便方法直接计算，得到最优m取值为1.27。不同的文献对m的取值提出了不同的计算方法，有一种常用的方法是直接设m为2。我们使用模拟数据比较不同m值时的聚类效果。设置聚类个数为5，进行FCM聚类，以隶属度大于0.5作为变量被归类的阈值，聚类结果如表1所示。结果显示，m值增加，噪声变量的归类减少，但趋势变量聚类效果变差。而在m取值1.27时，既保证了所有的趋势变量都被正确聚类，又最大程度防止了噪声数据的聚类。

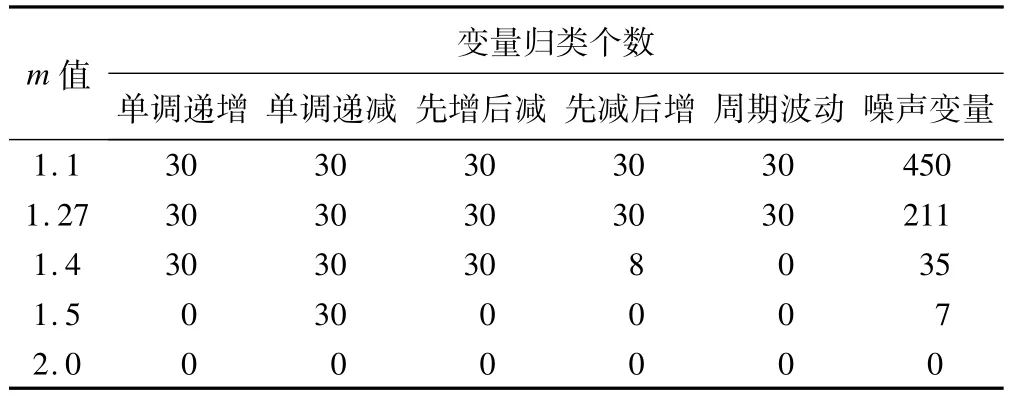
表1 模拟数据在设定不同m值时的FCM聚类结果

（2）模糊聚类个数选择

我们通过绘制最小类间距离随聚类个数变化的曲线来近似确定聚类个数。由于随着聚类个数的增加，最小类间距离下降，当聚类数目达到最佳时，其最小类间距离下降变慢，因此根据图中的拐点我们可以大致确定数据中存在的簇个数。如图1所示，当聚类数目达到5时，其最小类间距离便基本不再有明显下降，提示我们可将聚类数目设为5，这与我们的设定也是一致的。

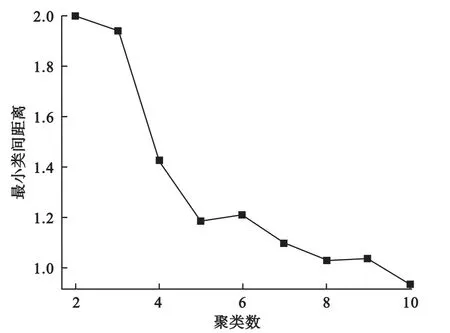
图1 模拟数据的最小类间距离随聚类个数变化曲线

（3）模糊C均值聚类分析结果

算法的输出为各个类的聚类中心及隶属度矩阵。结果显示，模拟设定的5种趋势变量分别以较大的隶属度属于5个不同的簇，而噪声变量则均以较小的隶属度随机归入各类。为了避免噪声变量的归类，我们进一步设定隶属度阈值，即变量只有在对某一类的隶属度大于某一阈值时才将其归入该类。如表2所示为设定不同隶属度阈值时的聚类结果。结果显示，当隶属度阈值增大时，噪声变量被归类的情况相应减少。如图2所示为隶属度阈值0.8时的趋势聚类结果。

表2 模拟数据在设定不同隶属度阈值时的FCM聚类结果

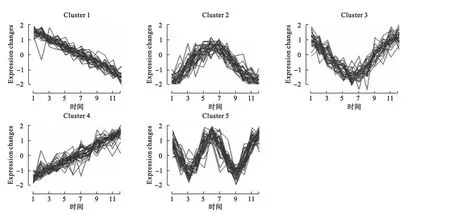
图2 设定隶属度阈值0.8时的趋势聚类结果

实例分析

为进一步说明模糊C均值聚类在动态组学数据动态趋势聚类中的应用，本文使用公开的细胞周期全基因组表达数据［9］。该资料包含在酵母菌细胞周期的17个时间点上测量的3000个基因表达数据，研究基因表达水平与细胞有丝分裂周期的关系。在进行FCM分析时，以不同基因作为聚类对象，基因在每个时间点上的均值作为其特征，数据格式如表3所示。

表3 酵母菌基因表达数据

分析步骤如下：

1.数据预处理

（1）缺失值处理。去除缺失大于25%的变量，共有49个变量被排除，对于其余的缺失值以该变量的均值填补；

（2）噪声滤除。为了更好排除噪声影响，我们将其中变异较小的变量（变量标准差小于0.5）滤除，以提高聚类效果，共有2379个变量被排除，最终变量数为572个；

（3）数据标准化。使每个变量其均数为0，标准差为1，以保证变化趋势相似的基因在欧氏空间上距离相近。

2.模糊系数的选择，计算可以防止随机变量归类的最小m值，得到最优m为1.15。

3.聚类个数的选择，通过绘制聚类个数的最小类间距离曲线（如图3所示），找到曲线拐点位置，确定最优聚类个数为12。

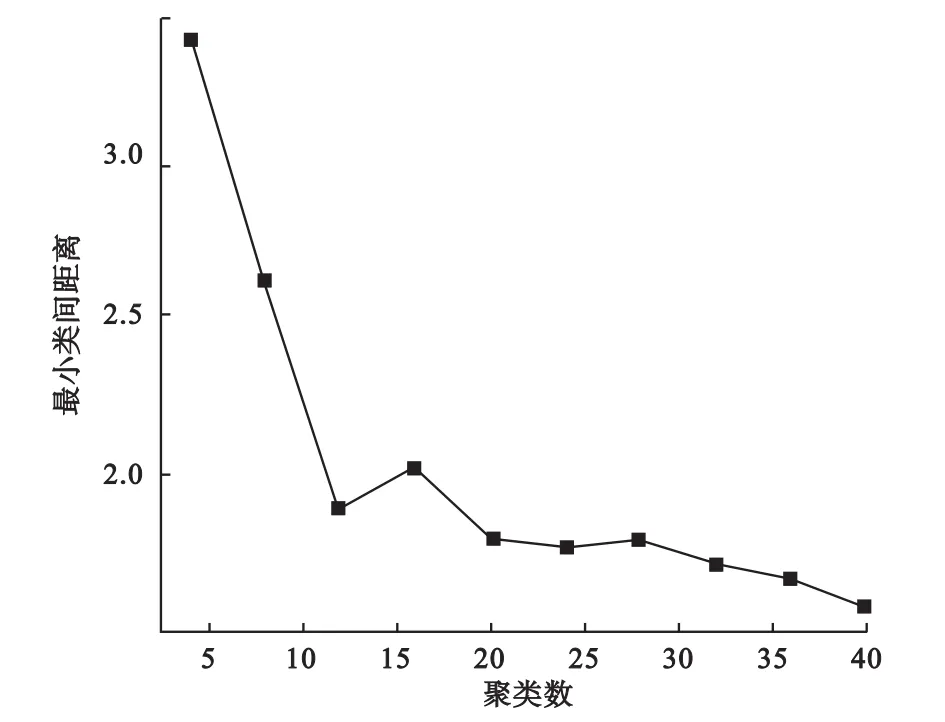
图3 动态基因表达数据FCM聚类最小类间距离随聚类个数变化曲线

4.设置m为1.15，C为12，使用FCM算法对预处理后的数据进行聚类。

得到隶属度矩阵，设置最小隶属度阈值0.8，则最终有325个变量被聚类，聚类1～聚类12的变量个数依次为：31、25、16、50、33、39、28、23、14、26、19、21，变量个数如表4，相应的聚类效果如图4所示。通过聚类效果图，我们可以清楚地看到各个类基因随时间变化的趋势，其中聚类2、聚类4和聚类9可以看到明显的周期趋势，可能为与细胞周期有关的关键基因。

更进一步分析，我们可以根据隶属度矩阵可以计算类间相关关系，计算公式为：其中Vkl表示第k类和第l类的相关关系，N为所有变量数，在这里为572，uik表示第i个体对第k类的隶属度。即对同时对于两类隶属度大的变量越多，则两类相关性越强。根据类间的关系，我们便可以获得全局的聚类结构。如图5所示为根据聚类中心矩阵进行PCA降维得到的全局聚类结构，其中类间连线表示类间相关，连线越粗表示相关性越强。可见，第6类和第9类相关性较强，第10类同时与第3类和第12类相关性较强，提示这些类的基因可能存在生物学关联。

图4 动态基因表达数据趋势聚类结果

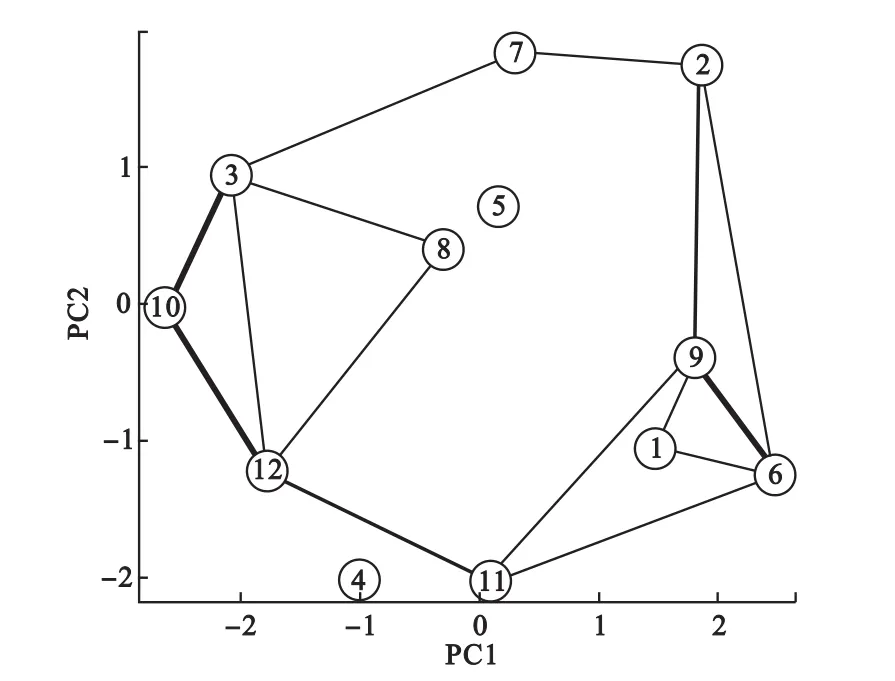
图5 动态基因表达数据聚类中心降维得到的全局聚类结构

讨 论

本文通过对模拟数据及实例的分析验证了模糊C均值聚类法对于动态设计组学数据中变量动态趋势识别的有效性。在模拟实验中FCM法准确的识别了我们设定的不同变化趋势，并且通过阈值的设定我们可以避免噪声的随机归类。而对于真实动态基因表达数据的分析显示了FCM方法可以识别表达模式相似的基因。组学数据维数较高，因此在聚类前进行滤除掉变异较小的变量，可以更好地避免噪声干扰，得到更理想的聚类结果。观察不同变化模式的聚类效果图，我们可以发现变化趋势更有意义的基因，例如与细胞周期相关的基因，并对其进行进一步研究。同时，由于聚为同一类的基因多具有相同功能，我们还可以根据已知功能的代谢物，推知某些未知基因，从而获得更多的生物信息［10］。因此说，FCM可以有效用于动态设计组学数据的预分析，帮助我们探索变化趋势相同的生物标记物，揭示变量之间的关系，为进一步探索生物信息提供依据。

但是模糊聚类法在也存在着一些问题，如需要设置模糊系数m和聚类数目C，及对初始聚类中心敏感，这些一直都是研究的重点和难点。对于m的设置，有一种普遍的做法是将m直接设置为2［11］，而本文通过对模拟数据的分析表明这种武断的做法会使聚类效果下降。而正确的方法应该是在防止随机变量被聚类和保证聚类效果之间取得平衡。对于聚类数目的设定，本文中使用簇个数的最小类间距离曲线［11］，对模拟数据的分析证明了其有效性。虽然这种方法在时间点过少，或类间重叠较大时并不总是有效的，但是仍然能帮助我们洞察数据中的簇个数。针对FCM的聚类效果对于初始聚类中心敏感，易陷入局部最优的问题，许多学者已经进行了大量的改进，如引入遗传算法，模拟退火等优化技术［12-13］，或通过对不同的初始聚类中心多次执行FCM算法选取最优结果。这些方法如何运用到动态组学数据分析并提高聚类效果还需要进一步研究。

1.Nicholson JCLK.Handbook of Metabonomic and Metabolomics.London：Elsevier，2007：174-179.

2.Futschik ME，Carlisle B.Noise-robust soft clustering of gene expression time-course data.J Bioinform Comput Biol，2005，3（4）：965-988.

3.Gasch AP，Eisen MB.Exploring the conditional coregulation of yeast gene expression through fuzzy k-means clustering.Genome Biol，2002，3（11）：RESEARCH0059.

4.Dembele D，Kastner P.Fuzzy C-means method for clustering microarray data.Bioinformatics，2003，19（8）：973-980.

5.Li X，Lu X，Tian J，et al.Application of fuzzy c-means clustering in data analysis of metabolomics.Anal Chem，2009，81（11）：4468-4475.

6.Bezdek JC.Pattern Recognition with Fuzzy Objective Function Algorithms.Norwell：Kluwer Academic Press，1981.

7.Kumar L，E FM.Mfuzz：a software package for soft clustering of microarray data.Bioinformation，2007，2（1）：5-7.

8.Schwammle V，Jensen ON.A simple and fast method to determine the parameters for fuzzy c-means cluster analysis.Bioinformatics，2010，26（22）：2841-2848.

9.Cho RJ，Campbell MJ，Winzeler EA，et al.A genome-wide transcriptional analysis of the mitotic cell cycle.Mol Cell，1998，2（1）：65-73.

10.Eisen MB，Spellman PT，Brown PO，et al.Cluster analysis and display of genome-wide expression patterns.Proc Natl Acad Sci USA，1998，95（25）：14863-14868.

11.Tan P，Steinbach M.数据挖掘导论.北京：人民邮电出版社，339，361.

12.聂生东，张英力，陈兆学.改进的遗传模糊聚类算法及其在MR脑组织分割中的应用.中国生物医学工程学报，2008（6）：860-866.

13.Richardt FK，Müller C.Connections between fuzzy theory，simulated annealing，and convex dualit.Fuzzy Sets and Systems，1998.

（责任编辑：郭海强）

Clustering the Dynamic Profile of Dynamic Omics Data Using Soft Clustering Method

Wang Lu，Zhang Tao，Liu Jia，et al（Department of Biostatistics，School of Public Health，Shandong University（250012），Jinan）

ObjectiveWe applied fuzzyC-means soft clustering to the clustering of dynamic profiles in dynamic omics data.MethodsSoft clustering was implemented here using the fuzzyC-means algorithm to reveal the dynamic profiles in both the simulated dynamic data and real dynamic gene expression data.Procedures to find optimal clustering parameters were developed.ResultsFCM was able to detect the dynamic profiles in both simulated data and real gene expression data.In addition，it can define the overall relation between clusters，and thus a global clustering structure.ConclusionFuzzyC-means clustering is an efficient tool to reveal the hidden structure in dynamic omics data.

Dynamic Omics data；FuzzyC-means cluster

本研究获国家自然科学基金资助（81302514）、山东省自然科学基金（ZR2013HQ056）

△通信作者：薛付忠，E-mail：xuefzh＠sdu.edu.cn