基于分段常数强度Markov模型的阿尔茨海默病进程研究*
山西医科大学卫生统计学教研室(030001) 孔盼盼 张慧敏 孙倩倩 余红梅
基于分段常数强度Markov模型的阿尔茨海默病进程研究*
山西医科大学卫生统计学教研室(030001) 孔盼盼 张慧敏 孙倩倩 余红梅△
目的将分段常数强度Markov模型应用于轻度认知损害(mild cognitive impairment,MCI)向阿尔茨海默病(Alzheimer′s disease,AD)转归过程中,深入研究影响转归过程的因素,为制定不同发展阶段的预防措施提供理论依据,为其他多状态慢性病不同发展阶段影响因素的探讨提供方法学借鉴。方法应用太原市600名社区老年人的4次随访资料,以MCI为状态1,中重度认知损害为状态2,AD为状态3,拟合分段常数强度Markov模型,分析MCI向AD转归不同发展阶段的影响因素,并根据模型计算3年转移概率矩阵。结果经假设检验,数据满足Markov性(P=0.89),不满足时齐性(P<0.001),应用分段常数强度Markov模型拟合,经多因素筛选,女性、年龄、吸烟、高血压和糖尿病是MCI向AD转归的危险因素,高文化程度和从事脑力劳动是MCI向AD转归的保护因素。由中重度认知损害向AD的转移概率随着随访时间的增加而增加。结论在数据满足Markov性,不满足时齐性时,分段常数强度Markov模型是对疾病转归过程的相关影响因素及其变化规律的有效分析方法。
多状态模型 非齐次Markov模型 分段常数强度Markov模型 轻度认知损害 阿尔茨海默病
阿尔茨海默病(Alzheimer′s disease,AD)是以近期记忆障碍为主要临床表现的神经变性疾病,常具有慢性进行性特征,是老年期痴呆的一个主要类型,约占老年期痴呆总数的2/3。轻度认知损害(mild cognitive impairment,MCI)是指个体存在轻微的认知障碍,但未达到痴呆标准且社会功能基本保持正常的认知损害状态,是介于正常老化和痴呆之间的一种中间过渡状态,是AD的高危人群。
多状态Markov模型(multi-state Markov model)是处理多状态资料的有效工具,可同时考虑所有的状态、结局、状态间转移的时间信息以及可能的影响因素,可连续性动态研究随机过程,分析影响疾病进展的因素,是迄今研究疾病进程的最佳模型[1]。与多状态Cox回归模型相比,多状态Markov模型最大的优势在于它能够处理无法观察到精确状态转移时间的资料。
许多研究AD的文献表明疾病进展率对时间的依赖性是增加的,因此AD各状态间的转移概率在时间上不是常量,即不满足时齐性的假设。本研究采用分段常数强度Markov模型分析不满足时齐性的多状态面板数据,研究阿尔茨海默病进程的影响因素,为今后类似研究提供方法学借鉴。
资料来源
1.研究对象
本研究沿用项目组前期随访的老年人群,共纳入60岁及以上社区轻度认知损害老年人600名,构成队列人群,分别于2010年11月、2011年5月、2011年11月和2012年5月共完成4次随访,进行问卷调查。
2.调查内容
(1)基本情况调查表由项目组自行设计,包括:①社会人口学指标:年龄、性别、受教育程度、婚姻状况、职业、经济收入、居住状况;②生活方式:吸烟、饮酒、社会活动、读书看报、体育活动、做家务、夫妻及子女关系;③健康状况:现患病、曾患病、家族遗传史及视力、听力、血压、体质指数。
(2)认知功能评定采用蒙特利尔认知评估量表(Montreal cognitive assessment,MoCA),它由加拿大CharlesLeMoyne医院神经科临床研究中心Nasreddine ZS根据临床经验并参考简易精神状况量表(MMSE)制订[2],是快速筛查痴呆高危人群——MCI的有效工具。
(3)状态划分
考虑到AD的发生和发展呈现进行性加重和不可逆性特点,结合本次研究流行病学调查的实际状况,将AD进程划分为三个状态:MCI(状态1),中重度认知损害(状态2),AD(状态3)。其中状态1和状态2为暂态,状态3为吸收态。根据王炜等[3]的研究结果,将19分作为MCI与中重度认知损害状态的截断值;根据张立秀[4]的研究结果,将15分作为中重度认知损害状态与AD的截断值。AD进程状态结构图见图1。
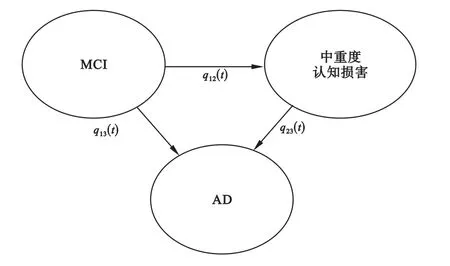
图1 AD进程状态结构图
原理与方法
1.Markov性检验与时齐性检验
Markov性假设是指未来的演变只取决于当前状态,而与个体过去的历史无关。
对于三个状态的模型,我们需证明在MCI状态(过去)上的逗留时间不影响中重度认知损害状态(当前)到AD状态(未来)的转移。
时齐性假设是假设Markov模型的转移概率矩阵不随时间变化。如果满足该假设,说明转移强度随着时间是不变的,则过程为齐次Markov过程(homogeneous Markov process);如果不满足该假设,说明转移强度随着时间是变化的,则过程为非齐次Markov过程(non-homogeneous Markov process)。
2.分段常数强度Markov模型
在数据满足Markov性,不满足时齐性时,应用分段常数强度Markov模型估计非齐次Markov过程:
假定队列有N个个体,对于每一个体c,状态间的mc次转移发生在时点

如果对每个个体观察到了mc次转移,那么就有最大值个时间点从一个状态到另一个状态的转移。将这些时间点排序,通过r个不同的截断点分成时间分区,保证在每个时间分区内至少能观察到一次状态间转移,形成一个时间分割序列{s1,…,sr}。因此,将随访时间分成r-1区间,每个区间内的转移强度矩阵假定为常数,即

其中Qk为每个区间内的常数矩阵。对每个区间用齐次Markov转移强度的最大似然法估计Qk[5]。对于两个连续的区间si≤t<si+1和si+1≤t<si+2,如果Qi=Qi+1,则认为满足齐性,从序列中删除时点si+1,将这两个区间合并,合并后继续与下一个邻近区间的转移强度进行比较;若不满足齐性则应视为分割点,如此反复,直至任意两个连续区间都不满足齐性为止。
设该模型的转移强度矩阵为Q,共有3个需要估计的转移强度:q12、q13、q23。

3.软件实现
资料的描述性分析使用SPSS13.0完成,Markov模型的拟合采用R(2.14.0)软件中的“msm”软件包和R(1.9.1)软件中的“tdc.msm”软件包完成,报告风险比及其95%置信区间。
结 果
1.研究对象基本特征
2007年筛选出的600例MCI老年人在3年后的2010年11月,经过四次随访到2012年5月,有二次及二次以上随访的有效数据为486例,失访25例,失访率为5.1%。其中12例搬迁、8例退出研究、5例死亡。
最终拥有完全数据的461例老年人中,男性150例(32.5%),女性311例(67.5%)。年龄最大者89岁,年龄最小者65岁,平均70.44岁(70.44±6.55),其中65岁至70岁者207人(44.9%),71岁至74岁者131人(28.4%),75岁及以上者123人(26.7%)。
2.Markov性检验与时齐性检验
根据R(1.9.1)软件tdc.msm软件运行结果,似然比检验统计量为0.02,自由度为1,P=0.89,说明该过程满足Markov性,可对该数据拟合Markov模型。
根据软件R(2.14.0)运行结果,似然比检验统计量为47.74,自由度为3,P<0.001,说明转移强度矩阵是随时间变化的,过程为非齐次Markov过程。
3.分段常数强度Markov模型拟合结果
由于数据满足Markov性,不满足时齐性,选择分段常数强度Markov模型进行拟合。根据选定各截断点后似然函数的比较及确保各个时间区间内都有合适的或足够的转移次数,该模型选择第三次调查的时间即12个月为截断点。
(1)分段常数强度Markov模型多因素分析
在第一个时间区间[0,12)月内,性别、年龄、文化程度、职业和高血压对状态1到状态2的转移有统计学意义;年龄、文化程度、职业、高血压和糖尿病对状态1到状态3的转移有统计学意义;性别、年龄、文化程度、高血压和糖尿病对状态2到状态3的转移有统计学意义。具体结果见表1。
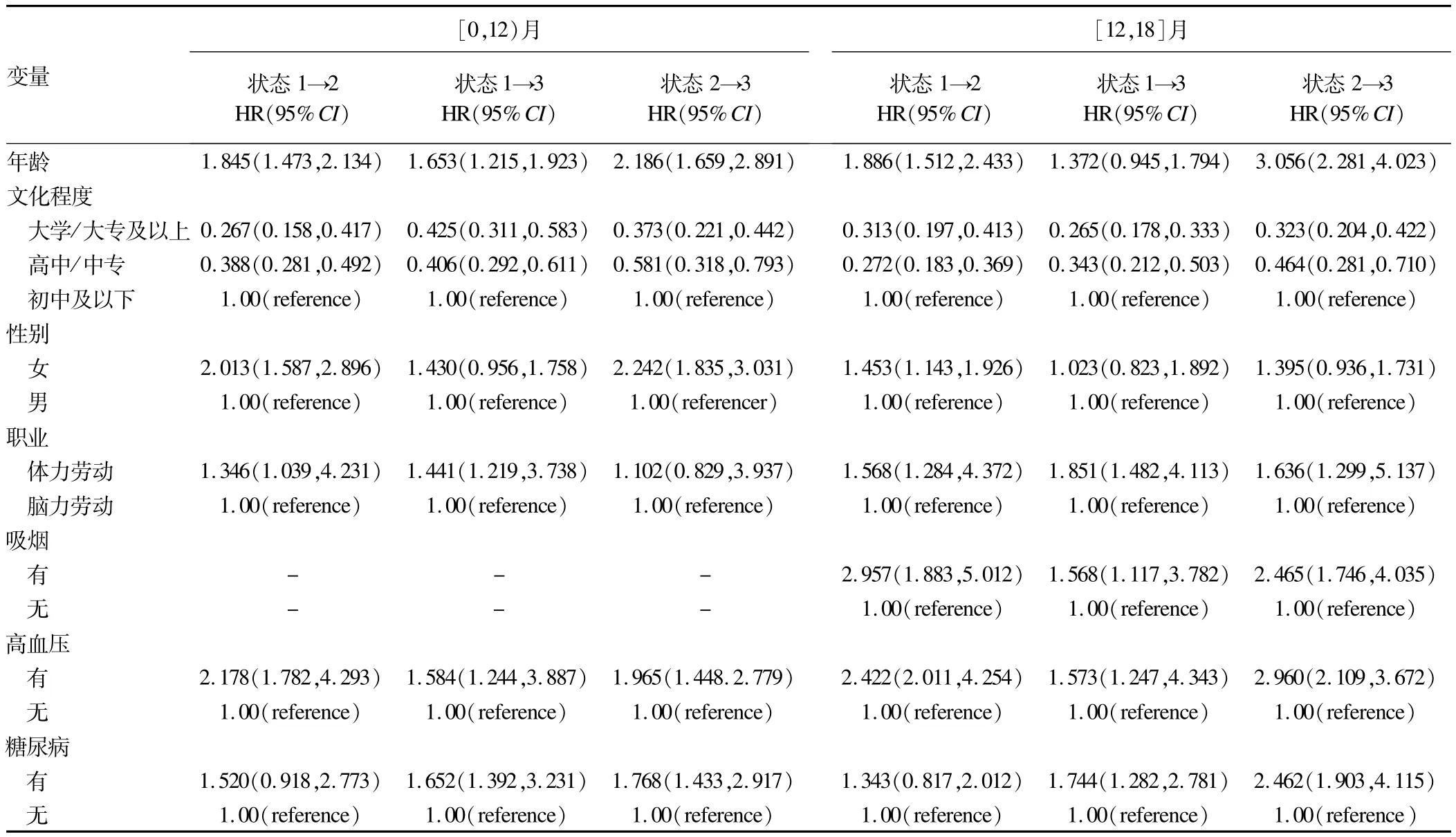
表1 分段常数强度Markov模型[0,12)月及[12,18]月多因素拟合结果
在第二个时间区间[12,18]月内,性别、年龄、文化程度、职业、吸烟和高血压对状态1到状态2的转移有统计学意义;文化程度、职业、吸烟、高血压和糖尿病对状态1到状态3的转移有统计学意义;年龄、文化程度、职业、吸烟、高血压和糖尿病对状态2到状态3的转移有统计学意义。具体结果见表1。
(2)模型评价
图2为危险因素作用下四个随访时点各状态的实际发生率曲线(实线)和利用模型拟合的理论发生率曲线(虚线),横轴代表观察时间,纵轴代表发生率。由图2可以看出,模型拟合情况较好。

图2 分段常数强度Markov模型拟合情况
(3)转归预测
两个时间区间分段常数强度Markov模型3年后转移概率矩阵分别见表2。结果显示,对于第一个时间区间,处于MCI状态的个体,3年后仍处于MCI状态的概率为35.5%,转移到中重度认知损害状态的概率为60.2%,转移到AD状态的概率为4.3%;对于处于中重度认知损害状态的个体,3年后仍处于中重度认知损害状态的概率为95.9%,转移到AD状态的概率为4.1%。

表2 分段常数强度Markov模型[0,12)月及[12,18]月3年后转移概率矩阵
对于第二时间区间,处于MCI状态的个体,3年后仍处于MCI状态的概率为12.8%,转移到中重度认知损害状态的概率为66.0%,转移到AD状态的概率为21.2%;对于处于中重度认知损害状态的个体,3年后仍处于中重度认知损害状态的概率为65.0%,转移到AD状态的概率为35.0%。
讨 论
1.非齐次Markov模型的优势
大多数研究在应用Markov模型时都假定其为齐次过程,即转移概率仅依赖于观察间经过的时间。时间齐次模型通常用于慢性病发展过程的研究,但是很明显这个模型在疾病自然史研究中有很严重的限制,这是由于转移概率在相当长的观察时间内始终保持恒定似乎是不太可能的,因此就需要使用一些非齐次模型。
估计非齐次Markov过程有两种常用的方法,除上述介绍的分段常数强度Markov模型外,还有一种是时间转换模型。非齐次强度矩阵是基线齐次强度矩阵和一个时间函数的乘积[6]。时间经函数变换后,非齐次过程就转化为齐次过程。此方法需要估计转移强度矩阵和时间函数的参数。与分段齐次模型相比,它需要估计的参数较少而且需要观察的转移较少。另外,它不需要假设离散时间间隔内的齐次性。Hubbard等(2008)[7]提出两种时间转换方法,指数时间转换和非参数时间转换。尽管这种方法看似比较巧妙,但它的限制性很强,因为所有的转移强度都按照一种形式建模,其中时间函数对所有的转移强度都是固定的。然而,实际上,通常发现的随机过程是转移强度随着时间有不同的趋势的,即每一个转移强度通过不同的函数来建模[8]。当认为所有转移强度随着时间连续变化不现实时,分段常数强度模型为首选。
2.应用分段常数强度Markov模型时需注意的问题
应用分段常数强度Markov模型时要注意的一个问题就是考虑分多少个区间。本研究采用的方法是考虑了两个区间,然而随访时间可以分成三个、四个甚至更多的区间来定义常数转移矩阵,每个研究者选择的区间数可能不同。因此需根据选定各截断点后似然函数的比较及确保各个时间区间内都有合适的或足够的转移次数等原则,选择合适的区间数和截断点。
3.本研究的不足之处
软件R(1.9.1)中的软件包tdc.msm[9]是目前唯一可用的进行Markov性检验的软件工具,由于其不允许数据有缺失的情况,所以随访人群中有缺失数据的25例患者并未纳入分析中,有可能会导致偏倚。
1.Andersen PK,Perme MP.Inference for outcome probabilities in multi-state models.Lifetime Data Analysis,2008,14(4):405-431.
2.Nasreddine ZS,Phillips NA,Bedirian V,et a1.The Montreal Cognitive Assessment,MoCA:a brief screening tool for mild cognitive impairment.Journal of the American Geriatrics Society,2005,53(4):695-699.
3.王炜,刘丹丹,解恒革,等.蒙特利尔认知评估量表(中文版)在驻京军队离退休干部中界值划分的初步研究.中华保健医学杂志,2010,12(4):271-273.
4.张立秀,刘雪琴.蒙特利尔认知评估量表中文版广州市老人院人群划界分探讨.中国心理卫生杂志,2008,22(2):123-125,151.
5.杨珊珊,李新毅,周立业,等.基于多状态Markov模型的老年人认知损害转归研究.中国卫生统计,2012,29(4):516-519.
6.Kalbfleisch JD,Law less JF.The analysis of panel data under a Markov assumption.Journal of the American Statistical Association,1985,80(392):863-871.
7.Hubbard RA,Inoue LYT,Fann JR.Modeling nonhomogeneous Markov processes via time transformation.Biometrics,2008,64(3):843-850.
8.Ricardo OR.Non-homogeneous Markov processes for biomedical data analysis.Biometrical journal,2005,47(3):369-376.
9.Meira-Machado L,Cadarso-Suárez C,deJ.tdc msm:an R library for the analysis of multi-state survival data.Computer methods and programs in biomedicine,2007,86(2):131-140.
(责任编辑:郭海强)
Piecewise Constant Intensities Markov Model in Outcome of Mild Cognitive Impairment to Alzheimer′s Disease
Kong Panpan,Zhang Huimin,Sun Qianqian,et al(Department of Health Statistics,Shanxi Medical University(030001),Taiyuan)
ObjectiveThe aim of this study was to introduce piecewise constant intensities Markov model in outcome prediction from mild cognitive impairment(MCI)to Alzheimer′s disease(AD)and to find out related factors in order to provide theory basis for AD prevention among various progressive stages.The suggested method for exploring influencing factors for various progressive stages of other chronic disease was also provided.MethodsOur data came from four waves of cohort study of 600 community dwelling older people in Taiyuan.MCI,moderate/severe cognitive impairment,and AD were defined as state 1,2 and 3,respectively.Piecewise constant intensities Markov model was applied to explore factors for various progressive stages from MCI to AD.According to the fitted model,three years transition probabilities among states were also estimated.ResultsBased on hypothesis testing,the Markov assumption was satisfied(P=0.89)and the time-homogeneous assumption was not(P<0.001),so piecewise constant intensities Markov model was applied.Multivariate analysis showed that women,older,smoking,hypertension and diabetes were risk factors for progression from MCI to AD while high education and intellectual work were protecting factors.The transition probability from moderate/severe cognitive impairment to AD may increase as follow-up time extending.ConclusionPiecewise constant intensities Markov model is an effective analysis method to the data when the Markov assumption was satisfied and the time-homogeneous assumption was not for related factors analysis and variation pattern during disease progressive process.
Multistate model;Non-homogeneous Markov model;Piecewise constant intensities Markov model;Mild cognitive impairment;Alzheimer′s disease
国家自然科学基金资助项目(81373106)
△通信作者:余红梅,Email:yu_hongmei@hotmail.com

