运用多元统计分析法评价医院综合服务能力

柳丰杰程繁银张福良于丽萍

运用多元统计分析法评价医院综合服务能力

柳丰杰1程繁银2，△张福良2于丽萍3

采用多元统计分析的方法定量地评价医院的综合服务能力，能克服传统医院评价方法的片面性，是医院综合服务能力评价的一个新尝试。本文用聚类分析、主成分分析的方法对某市十所二级综合医院进行分类，并按医院综合服务能力优劣排序，分析结果与被评价医院的实际综合服务能力基本吻合，得到了预期效果。

聚类分析 主成分分析 综合评价

为了加强医疗机构建设和管理，促进其持续改进，提高医疗质量，保证医疗安全，更好地满足人民群众多层次的医疗服务需求，开展对医院综合服务能力评价体系建设十分重要。目前对医院综合服务能力的评价大多往往只是通过对诸多方面打分后的分数累加进行评价，相对比较简单，不能很好地反映一个医院的工作情况。本研究通过采用多元统计分析的方法定量地评价医院的综合服务能力，从而提高了评价的科学性和客观性，弥补了简单分数累加带来的片面性等问题，是一种对医院评价的新尝试［1］。

资料与方法

本文的研究对象是辽宁省某市的十所二级综合医院，评价内容及标准选用国家卫生部2012年颁布的《二级综合医院评审标准实施细则（2012）》（以下简称细则）中的指标与评定标准。评价指标包括六大类指标：医院功能任务（A）、医院服务（B）、患者安全（C）、医疗质量安全管理与持续改进（D）、护理管理与质量持续改进（E）、医院管理（F）。每类指标下包括若干亚指标，各指标有明确的四个等级评定标准［1］。

在辽宁省内选择六名医院管理相关专家，专家根据《细则》的各个项目和标准对医院进行逐项评价打分，将得到的各亚指标的得分按照百分比转化为各大类的综合得分，然后再用多元统计分析法进行评价。专家评价方法包括访谈法、观察法、抽样调查等。

结果与分析

1．六个指标的样本分类 将对十所医院的打分情况用SPSS统计分析软件进行聚类分析。聚类方法选择组间聚类（between-groups linkage），距离测度选择欧氏平方距离（squared Euclidean distance），由图1可见，取临界值λ＝15．02，则10个样本被分成如下三类：

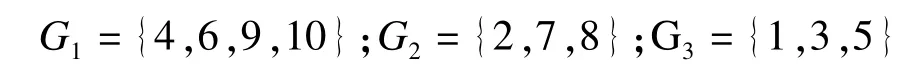
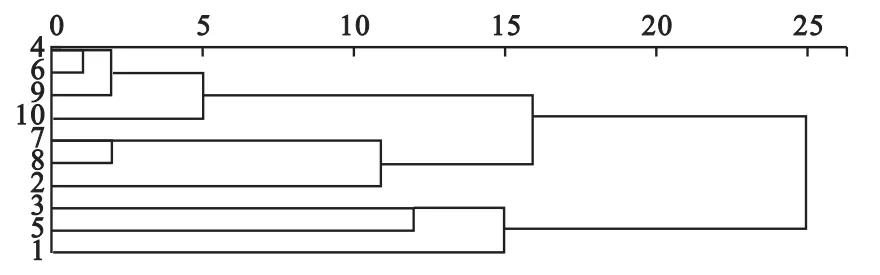
图1 六指标聚类图

2．主成分聚类 为避免指标间高度相关的干扰，需对样本进行主成分聚类。由原始数据可计算出相关系数阵R及R的特征值，并计算出各因子方差占总方差的百分比（方差贡献率）及累计百分比［2］（累计方差贡献率）（略）。前3个主因子的方差占总方差的百分比分别为48．6%、27．18%、11．85%，累计方差贡献率为87．6%，故提取3个主因子可得到因子变换矩阵。3个主因子彼此独立可做为聚类指标，每个样本的三个主坐标计算如下：

式中A，B，C，D，E，F分别对应上述《细则》中的六个指标。对10个样本（每个样本3个主坐标）聚类，聚类方法选择组间聚类，距离测度选择欧氏平方距离，由图2可见，取临界值λ＝19时，10个样本被分成如下三类：

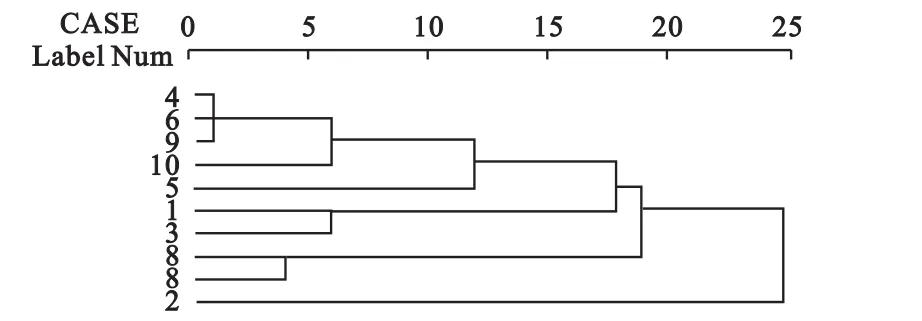
图2 3个主成分聚类图

主成分分类结果：G1＝｛2｝；G2＝｛7，8｝；G3＝｛1，3，4，5，6，9，10｝，其中2号医院综合服务能力为上层，7号和8号综合服务能力为中层，其他较差。

3．将样本按综合服务能力排序

用因子分析的方法，根据原始数据求出六个指标的相关系数矩阵R及R的特征值、各因子方差占总方差的百分比及累计百分比，使累计百分比超过85%，同时经方差最大正交旋转变换得到三个主因子构成的因子模型（因子载荷矩阵），见表1。

根据表1和（1）式，用SPSS软件计算出每一个样本的正交因子得分，如第1个样本得分为（－1．23099，－1．73308，－0．74425），然后以各因子的贡献率为权重，对各因子加权求和，求出各样本的综合得分值

以此类推，求出其他yi值，yi值越大该号样本（医院）评分越高，各医院评分排序结果见表2［2－3］。

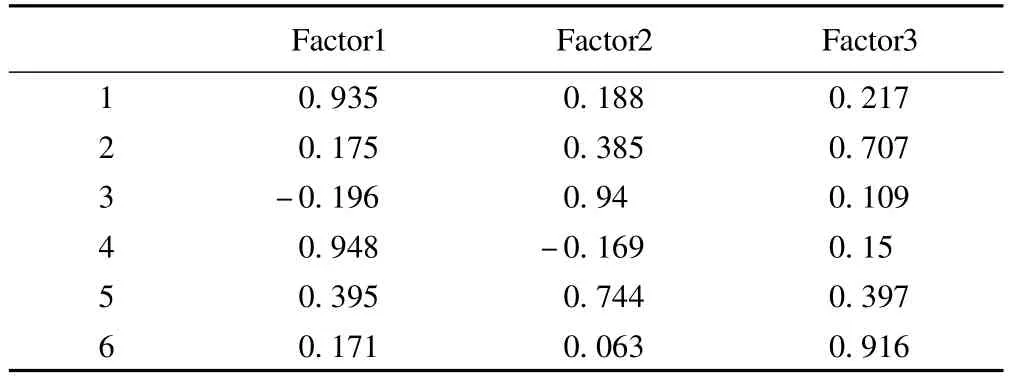
表1 因子载荷矩阵

表2 各医院评分排序结果

讨 论

1．比较六指标分类与主成分分类结果可知，两种分类结果是有差异的。这种差异主要是来源于指标间的相关性，由于主成分能避免指标间相关性的干扰，因此主成分分类结果更可信。

2．六项医院管理指标的取值采用百分比形式表述，其优点是能避免指标间不同量纲的影响，所得评价结果更加客观真实。

3．文中采用组间聚类、距离测度选择欧氏平方距离。除此之外本文也采用组内聚类、距离测度选择欧氏距离，所得主成分分类结果与文中结果一致，说明主成分分类结果是稳定的。

4．在综合管理水平评价问题中，各指标的权重评估是十分重要的。如果不进行各指标的权重评估，将各指标重要性等同看待显然是不合理的，所得评价结果不能令人信服。如何确定各指标的权重是每个评价者必须要解决的问题，本文采用多元统计分析中的主成分法计算各因子方差占总方差的百分比分别为48．6%、27．18%、11．8%，三者累计百分比为87．58%，确定主成分数为3个。据此权重及（2）式计算出各样本的综合得分值y1，y2，y3…，y10，这里yK值的获得考虑了主成分综合指标的权重，因此所得医院管理水平的综合排序是客观合理的。

5．由表2的排序结果可知，若将10个样本分成三类则分类结果与主成分聚类结果完全一致，G1＝｛2｝（样本排序第一）；G2＝｛7，8｝（样本排序第二、第三）；G3＝｛1，3，4，5，6，9，10｝（样本排序靠后）。这进一步验证了本文分类结果的可行性，说明按主成分及因子分析的方法对十家医院排序所得的结果是令人信服的。

多元统计分析方法采用定量分析的方法，从不同侧面、不同角度、全方位地分析、评价问题；避免主观人为因素的干扰，使评价结果更加客观、准确，是综合评价医院管理水平一种行之有效的方法［3－5］。

［1］卫生部．二级综合医院评审标准（2012年版）实施细则．

［2］董平，张敬华．多元统计分析在医院管理中的应用．数理统计与管理，2001，20（5）：24-25．

［3］张梦溪．用多元分析法评价手机质量．统计与决策，2005，191（6）：124．

［4］张庆利．SPSS宝典．第2版．北京：电子工业出版社，2011．

［5］张林．基于多元统计分析的浙江经济发展研究．浙江农业科学，201l，20（3）：716-718．

（责任编辑：郭海强）

1．大连医科大学附属第二医院（116023）

2．大连医科大学公共卫生学院（116044）

3．大连大学附属中山医院（116000）

△通信作者：程繁银，E-mail：chengfanyin＠163．com