时间序列分解法在我国食物中毒发病人数预测中的应用

华北理工大学公共卫生学院（063000） 王永斌 李向文 田珍榛 袁聚祥

时间序列分解法在我国食物中毒发病人数预测中的应用

华北理工大学公共卫生学院（063000） 王永斌 李向文 田珍榛 袁聚祥△

目的对ARIMA模型和时间序列分解预测方法在我国食物中毒发病人数预测中的效果进行比较，探讨优化模型，为更好地了解我国食物中毒发病人数提供预警和参考依据。方法收集2000－2013年我国食物中毒季度发病人数，用Excel2003和SPSS 20．0拟合ARIMA模型和时间序列分解预测模型，用2013年的数据评价模型的预测效果，并对2014年各季度食物中毒发病人数进行预测。结果两种方法预测食物中毒发病人数的R2分别是0．355和0．919；MRD分别为34．350%和14．507%；MER分别为0．303和0．110；MSE分别为293505．000和43570．000；RMSE分别为541．761和208．736；MAE分别为413．500和149．500；预测的2014年各季度食物中毒发病人数依次为387、1020、1357、606。结论时间序列分解法预测效果优于ARIMA模型，可以用来预测我国食物中毒的发病人数，预测效果可靠。

ARIMA模型 分解分析法 食物中毒 发病人数 预测

近年来，卫生部门每年接到食物中毒报告100～200起，涉及千余人发病，百余人死亡，越来越引起社会关注。因此，为了更好地了解我国食物中毒人数，本文利用ARIMA模型和分解预测方法对我国2000－2013年食物中毒季度发病人数建立预测模型，比较两种预测方法对于我国食物中毒发病人数预测的准确性，从而为更好地了解我国食物中毒发病人数提供预警和参考依据。

资料与方法

1．资料

资料来源于2000－2013年我国卫生部关于重大食物中毒情况通报资料。

2．ARIMA模型预测［1］

（1）识别：通过相关的分析来确定时间序列的随机性、季节性和平稳性，最终结合实际情况，选定最优的模型对数据进行分析。

（2）参数的估计和诊断：依据赤池信息准则（AIC）和Schwarz贝叶斯准则（SBC）确定模型阶数，建立预测模型。在不断改变模型的阶数后，AIC与SBC值最小的模型为最佳模型。

3．时间序列分解预测

分解预测是适合含有趋势、季节、循环多种成分序列预测的一种古典方法。预测步骤：

（1）确定并分离季节成分①计算季节指数，以确定时间序列中的季节成分、随机波动（ERR）、季节周期因子（SAF）、长期趋势（STC），②将季节成分从时间序列中分离出去，计算季节调整后的序列（SAS），即用每一个观测值除以相应的季节指数，以消除季节性；

（2）对消除季节成分的序列建立预测模型进行预测；

（3）计算出最后的预测值：用预测值乘以相应的季节周期因子，得到最终的预测值［2］。

4．两种模型拟合效果比较及预测应用

基于2000－2012年我国食物中毒季度发病人数建立预测方法，使用2013年数据进行外回带验证。评价拟合和预测的指标包括［3］决定系数（R2），相对误差（RD），平均相对误差（MRD），平均误差率（MER），均方误差（MSE），均方根误差（RMSE）和平均绝对误差（MAE）。选取R2较大及MRD，MER，MSE，RMSE和MAE都较小的方法，预测我国2014年食物中毒季度发病人数。

5．统计学分析

运用Excel 2003和SPSS 20．0进行相关的分析，检验水准α＝0．05。

结 果

1．ARIMA模型预测结果

我国食物中毒发病人数具有明显的周期性和季节性波动。所以首先进行对数转换和sd＝1的季节差分，d＝1非季节差分分别消除季节和趋势的影响以获得稳定的方差和均值，从而获得平稳的序列。再结合经过对数转换和季节差分的ACF和PACF图（图1），残差情况，以及系数之间的相关性选取AIC和SBC较小，对数似然函数值较大，且模型各参数均有统计学意义的模型为较优模型，通过比较，结合实际情况得到最优的模型是ARIMA（1，1，1）×（1，1，0）12。模型参数估计结果见表1，且在所有满足条件的模型中AIC＝62．232，SBC＝69．960，为最小，对数似然函数值为－27．116，为最大。结合残差的ACF和PACF图（图2）和残差序列Box-Ljunt统计结果显示统计量差异均无统计学意义（P＞0．05），提示残差是随机分布的。以此模型对2000－2012年的数据进行拟合，然后对实际值和拟合值进行配对t检验，得出t＝－0．256，P＝0．799＞0．05，可以使用该方法对我国食物中毒的季度发病人数进行预测。2013年预测和外回带验证结果如表2。

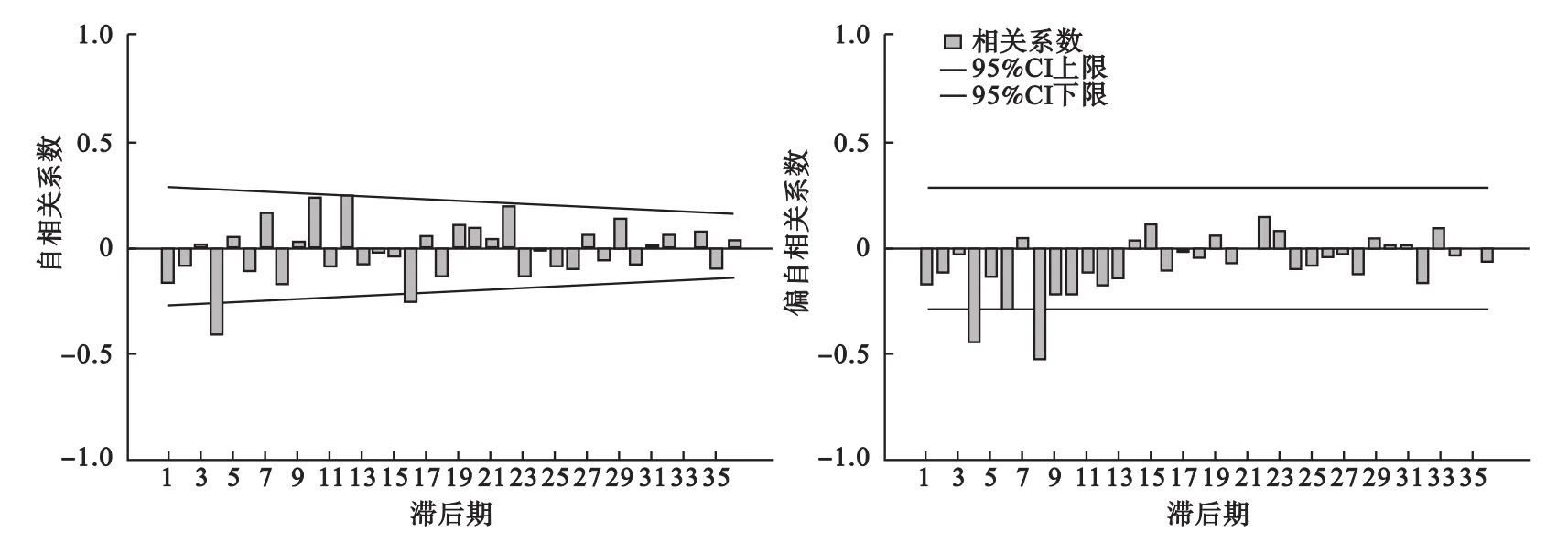
图1 原始序列经过对数转换，d＝1，sd＝1差分后的ACF和PACF图

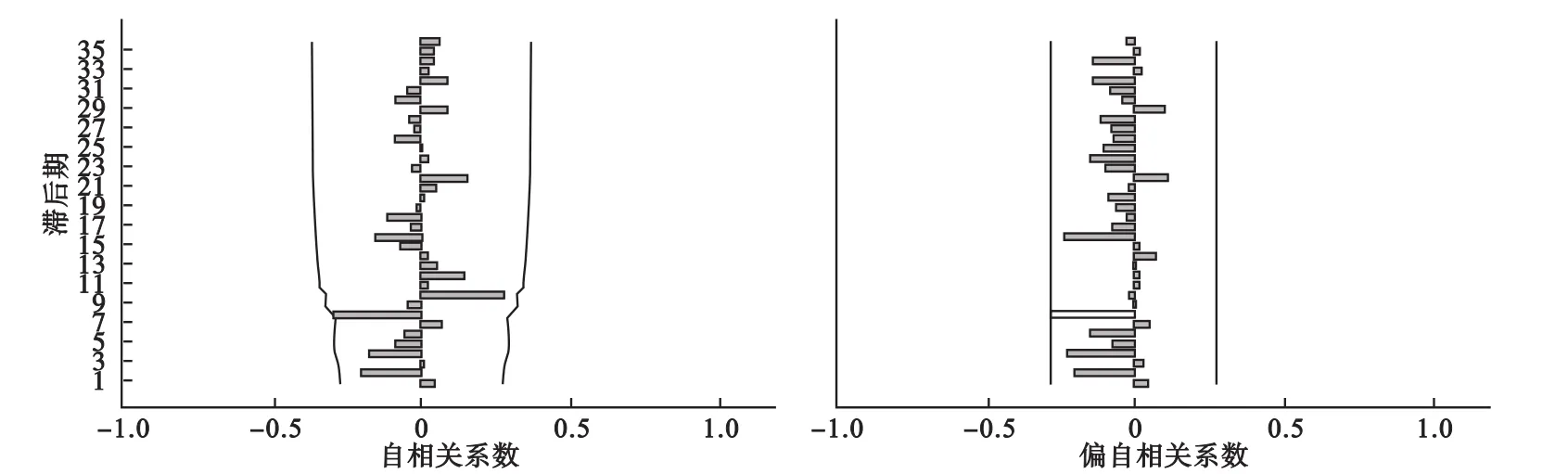
图2 ARIMA（1，1，1）×（1，1，0）12残差序列的ACF和PACF图

表1 ARIMA（1，1，1）×（1，1，0）12模型的参数估计与检验

2．时间序列分解预测结果

对原始数据分解出时间序列中的季节成分：季节调整后的序列和长期趋势（图3），随机波动和季节周期因子（图4）。从图3、图4可知：①我国食物中毒季度发病人数在2006年以后总体呈下降趋势，并存在一定的规律性波动；②2001年一些突发性事件导致的食物中毒季度发病人数异常波动比较剧烈，结合食物中毒季度发病人数实际走势来看，在食物中毒季度发病人数出现较大幅度增加或减少的时期，随机波动对食物中毒季度发病人数的影响较明显。经归一化处理后ERR、SAF、STC 3种波动成分对食物中毒季度发病人数的贡献率［4］分别为：0．0375%、0．0380%、99．924%；根据季节调整后的序列使用曲线拟合的方式建立预测方程1＝1130．724＋227．560t－6．425t2＋0．042t3；根据建立的方程计算出2013年一季度到四季度的趋势预测值，再根据季节因子一季度到四季度的季节周期因子分别为0．38552，1．12047，1．66014和0．83387，便可以估计出2013年一季度到四季度的食物中毒发病人数。预测和外回带验证结果如表2。用此方法对2000－2012年的数据进行拟合，对实际值和拟合值进行配对t检验，得出t＝-0．081，P＝0．935＞0．05，说明实际值和拟合值差异无统计学意义，可以使用该方法对我国食物中毒的季度发病人数进行预测。

表2 2013年我国食物中毒季度发病人数外回带验证结果

3．两种方法预测效果比较

由表3可知分解预测方法的预测精度明显优于ARIMA模型预测方法。比较两种方法的拟合误差曲线，见图5，可见分解预测方法误差更接近0且更稳定。图6为两种方法的拟合曲线，可见分解预测方法的拟合曲线与实际值曲线更接近。对两种方法拟合的我国2000－2012年的数据进行配对t检验，得t＝2．638，P＝0．021＜0．05，说明使用这两种方法对我国食物中毒的季度发病人数进行拟合，两种方法对食物中毒发病人数拟合值差异有统计学意义。

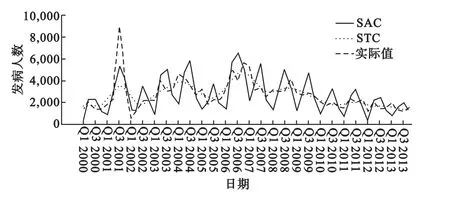
图3 2000－2012年我国食物中毒季度发病人数SAS，STC分解序列

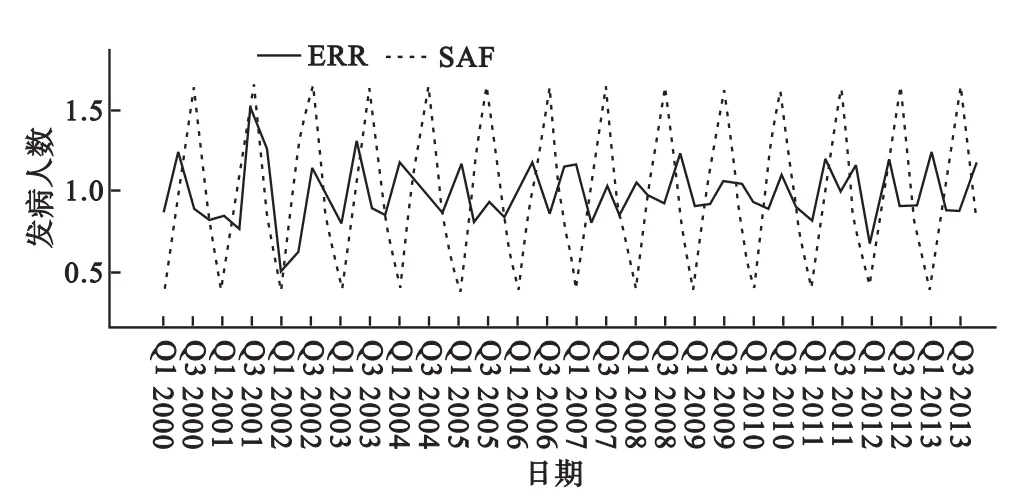
图4 2000－2012年我国食物中毒季度发病人数ERR，SAF分解序列

图5 两种方法拟合误差曲线

图6 两种方法的拟合预测曲线

4．预测应用

选用时间序列分解预测方法对我国2014年食物中毒发病人数进行预测，结果如表4。

表3 两种方法预测效果比较

表4 2014我国食物中毒发病人数预测值

讨 论

已经有相关研究［5－7］使用ARIMA模型对食物中毒事件数进行了预测，为了寻找更好的模型预测食物中毒发病人数。本研究尝试使用ARIMA模型和时间序列分解预测方法对食物中毒季度发病人数进行了拟合与预测，研究结果表明分解预测方法预测效果明显优于ARIMA模型预测结果，且分解预测的拟合值与实际值的走向基本一致，尤其在2002年以后，拟合值与实际值表现出极为相似的升降规律，分解预测较好的拟合了我国食物中毒的季度发病人数的变化规律，显示了较高的预测精度，可以较好地在数理层面对食物中毒发生情况进行预测［3］。分解预测方法分离出了时间序列的季节成分。相关报道［7］指出预测的MRD≤5%时为理想状态，但本文使用2013年的数据对分解预测方法进行外回带验证表明：本文MRD还是稍大（MRD＝14．507%）。这可能主要因为：①食物中毒的发生受到多种因素影响，识别其发生的所有特征常比较困难；②从分解的随机序列图可以看出，随机性波动对食物中毒季度发病人数的影响较明显；③食物中毒的发生受到一些突发因素影响。因此，在预测我国食物中毒发病人数方面，能考虑随机波动和一些突发因素的更优的预测模型仍须进一步研究和验证，以便提高预测的准确性和稳定性。

本研究中ARIMA模型预测误差较大，其主要原因可能是：ARIMA模型适用于短期、不带季节变动的反复预测，而我国食物中毒发病人数具有明显的季节变动趋势。

综上所述，可以借助分解预测的方法，结合实际情况，对我国食物中毒发病人数进行早期预测、预警，为食物中毒防控工作提供参考依据，从而减少或者消除决策的盲目性。但值得注意的是：单次分析建立的分解预测模型，不能作为永久不变的预测工具，只能用于短期预测。在实际工作中，应收集足够的时间序列数据，用新的实际值对已建立的模型进行验证，并应不断加入新的实际值，以拟合更能反映实际情况的食物中毒发病人数预测模型［8］。

［1］孙振球．医学统计学．第3版．北京：人民卫生出版社，2009：261-277．

［2］贾俊平．统计学．第1版．北京：清华大学出版社，2004：356-386．

［3］戴钰．最优组合预测模型的构建及其应用研究．经济数学，2010，27（1）：92-98．

［4］赵安平，王大山，肖金科，等．蔬菜价格时间序列的分解与分析—基于北京市2002-2012年数据．华中农业大学学报：社会科学版，2014，10（1）：49-53．

［5］张哲，樊永祥．ARIMA模型在我国食物中毒事件预测中的应用．中国预防医学杂志，2012，13（8）：638-640．

［6］陈玲，徐慧兰．自回归求和移动平均模型在湖南省食物中毒预测中的应用．中南大学学报，2012，37（2）：142-146．

［7］Tian ZX，Zhang YS，Yan W，et al．Time-series analysis of the relationship between air quality，temperature，and sudden unexplained death in Beijing during 2005-2008．Chinesemedical journal，2012，125（24）：4429-4433．

［8］张国良，后永春，舒文．三种模型在肺结核发病预测中的应用．中国卫生统计，2013，30（4）：480-483．

（责任编辑：邓 妍）

△通信作者：袁聚祥，E-mail：yuanjx＠heuu．edu．cn