基于R软件的缺失数据MICE填补效果研究*

山东大学公共卫生学院流行病与卫生统计学系（250012） 章 涛 朱 麟 季加东 袁中尚 薛付忠 李秀君

基于R软件的缺失数据MICE填补效果研究*

山东大学公共卫生学院流行病与卫生统计学系（250012） 章 涛 朱 麟 季加东 袁中尚 薛付忠 李秀君△

目的研究不同缺失率、不同缺失机制下，MICE（multivariate imputation by chained equations）多重填补的效果，探讨该填补方法的适用情况。方法依托某现况调查的完全数据，使用R软件构造不同缺失率、不同缺失机制的缺失数据。计算列表删除和MICE多重填补后分析结果的标准偏倚，并进行比较。单独对分类变量计算多重填补后的平均错分率。结果在单变量缺失率分别为10%、20%和30%的随机缺失三种情况下，MICE多重填补表现优良；其他模拟情况下，MICE多重填补相比于列表删除并未表现出明显的优势。对于分类变量，MICE填补后的平均错分率均超过60%。结论对于随机缺失数据，且单变量缺失率不超过30%时，建议采用MICE多重填补进行处理；但对于资料中的分类变量，不建议直接引用MICE填补后的具体数值。

MICE 缺失数据 模拟研究 多重填补

缺失数据（m issing data）是指那些未被观察到的、对数据分析有意义的数据［1］。缺失数据可能会导致参数估计的偏倚，增大Ⅰ类或Ⅱ类错误。并且数据的缺失常伴随着信息的缺失，因此缺失值可能导致统计检验效能的降低［2］。目前缺失数据的处理方法大致分为三类［3－5］：删除法、填补法和不处理。删除法包括列表删除（listw ise deletion，LD）和配对删除。填补法又可分为单一填补和多重填补。不处理的方法包括贝叶斯网络和人工神经网络的方法等［6－7］。

多数统计软件在进行缺失数据的分析时默认采用列表删除法，因而在实际应用中最常用的缺失数据处理方法之一还是列表删除。列表删除，即删除含有缺失变量的观测。单一填补方法尽管简单，但可能会导致目标变量分布的扭曲，并且无法解释填补的不确定性。而多重填补（multiple imputation，MI）在一定程度上可以克服这些不足。

多重填补的方法较多，近些年发展了一种新的多重填补方法——MICE多重填补。该方法的基本思想是全条件定义法（fully conditional specification，FCS）。相比于一般的MI方法，MICE多重填补由于其在算法上的优化而具有更快的收敛速度，节省了运算时间。该方法并不依赖于数据满足多元正态分布的假定，对填补模型的设定也不是很严格，即使在填补模型并不非常适合原始数据类型时也能取得较好的填补效果。此外，MICE多重填补能够处理多种数据类型，具有灵活的适用性［8－10］。MICE多重填补在Van Buuren［9］的模拟研究中表现出了很好地处理缺失数据的能力。在实际应用中MICE多重填补也具有不错的表现［11－12］，且MICE多重填补在软件中实现起来语句简单，存在着较好的应用潜力［13］。但Van Buuren仅研究了在MAR缺失机制下的填补效果［9，14］。本研究旨在进一步探究在不同缺失率、不同缺失机制下MICE多重填补处理缺失数据的效果以及MICE多重填补的适用情况。目前可以实现MICE多重填补的软件包括R软件的mice程序包（package）和Stata软件，由于Stata软件属于收费软件，故本次研究采用R软件实现。

资料与方法

1．MICE多重填补原理［14］

假设完整数据Y是从含p个变量的多变量分布P（Y｜θ）中随机抽取的观测值，其中θ为未知参数向量，它决定了Y的分布。因此，只要我们得到θ的分布，便可从P（Y｜θ）中抽取数值进行缺失填补。在MICE填补中，θ的后验分布通过Gibbs迭代抽样得到。

具体做法为：从观察到的边际分布开始，进行t次迭代的Gibbs抽样，第t次迭代时得到：

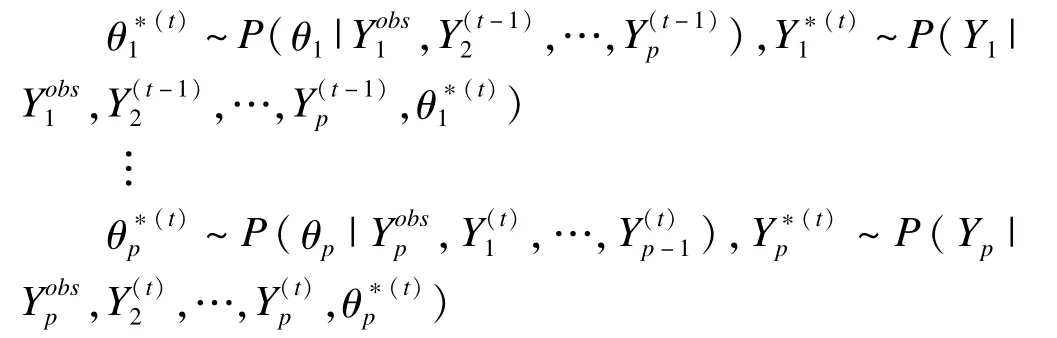
对于填补后的多个完整数据集，根据Rubin的理论，mice包提供了语句可以对每个数据集分别进行统计分析，最后将多个分析结果综合起来。

2．资料情况

依托某现况调查的数据进行缺失模拟。该数据中包含多个变量，本次研究选取数据中区域分布（x1）、平均处方费用（x2）、配备国家药物目录西药品种数（x3）、配备省增补药物目录西药品种数（x4）、医生平均收入水平（y）等5个变量，共522条观测。其中x1为二分类变量，x2、y为连续型数值变量，x3、x4为离散型数值变量。所有观测均无缺失值。

3．模拟思路

缺失数据根据其缺失机制，可分为完全随机缺失（missing completely at random，MCAR）、随机缺失（missing at random，MAR）和非随机缺失（notmissing at random，NMAR）［2，15－16］。不同缺失机制，会影响缺失值填补效果。故本研究模拟了各种缺失机制下，单个变量缺失率（缺失率＝某变量中缺失值个数／完全数据中该变量的值个数）分别为10%、20%和30%的各种数据。

MCAR：所缺失的数据发生的概率，既与已观察到的变量无关，也与未观察到的数据无关。故采用完全随机的方法在完整数据集中制造缺失。

MAR：缺失数据发生的概率与所观察到的变量值有关，而与未观察到的数据的特征无关。因此在本数据中依据医生平均月收入，将收入水平进行从小到大排序以后，按顺序分为5个收入等级，按收入等级由低到高，对每个等级的其他变量赋予一定的缺失概率。不同等级的缺失概率取值分别为p1～p5，具体见表1。

NMAR：当缺失数据既不属于MCAR，也不属于MAR，我们就称该缺失属于NMAR。NMAR数据的缺失概率，多依赖于缺失值本身。因此在本数据中，各变量的缺失概率按变量值自身大小分别给定相应的缺失概率。具体做法为：针对数值型变量，对每个变量从小到大排序，按顺序分为5个等级，对每个等级赋予一定的缺失概率，不同等级的缺失概率取值分别为p1～p5；对于二分类变量（区域分布x1），由于只有两个变量值，故根据其数值不同，赋予两个缺失概率（p6～p7），据此随机产生缺失。

不同的变量缺失率通过不同的缺失概率搭配实现。为保证结果的可靠性，对每种缺失类型、缺失率都进行500次的模拟。

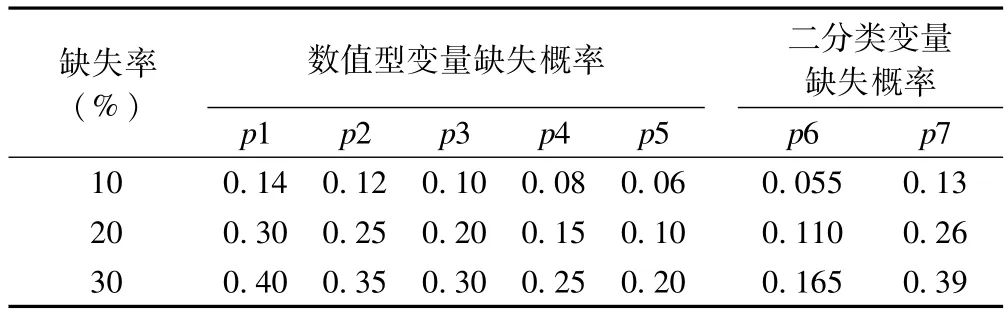
表1 不同缺失率下的缺失概率搭配

4．分析及评价方法

本研究中以y为因变量，其他所有变量为自变量，采用多元线性回归的方法对数据进行统计分析（对原始完整数据建立多元线性回归模型，模型及各变量均有统计学意义）。

产生缺失数据以后，分别使用列表删除和MICE填补，然后应用多元线性回归的方法进行分析。对各回归系数，计算其原始偏倚（bias）、标准偏倚［17－18］（standard bias，SB），变量x1～x4对应的标准偏倚为SB1～SB4。对于原始偏倚，采用均数±标准差（±s）进行描述。对于分类变量，计算多重填补后数据集的平均错分率。本研究中定义：错分率＝填补值与对应真实值不相等的个数／缺失值个数×100%。

5．评价标准

（1）分类变量评价标准

优：平均错分率≤10%；良：10%＜平均错分率≤30%；中：30%＜平均错分率＜50%；差：平均错分率≥50%，此时多重填补效果与随机取值填补效果相当，甚至更差。

（2）多元线性回归结果评价标准

优：标准偏倚≤10%。此时缺失数据处理后的多元分析回归系数精确度高，准确度高；良：10%＜标准偏倚≤20%；中：20%＜标准偏倚≤40%；差：标准偏倚＞40%，此时偏差极大，可能会出现与真实情况相反的结果［17］。

结 果

1．分类变量填补效果

对于分类变量多重填补的效果，从表2中可以看出在任一种缺失机制下，三种缺失率对应的二分类变量平均错分率均超过60%。说明MICE多重填补对于分类变量值本身的填补效果不好。

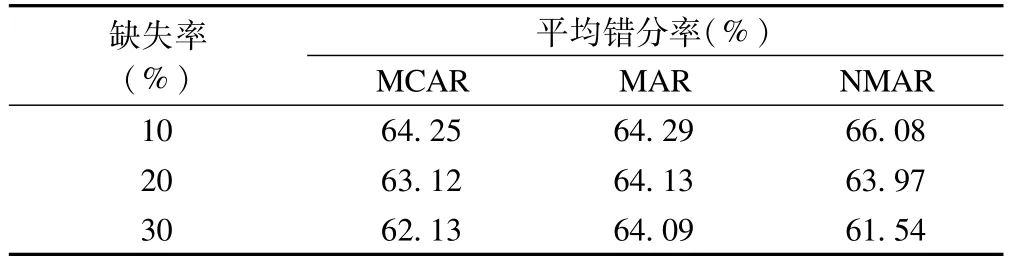
表2 分类变量的错分情况

2．填补后多元线性回归分析结果

不同缺失机制下，应用多元线性回归后，各变量的回归系数偏倚情况见表3～5。

（1）完全随机缺失（表3）

在当前的教学模式下，教师在讲授相关理论知识时，普遍采用的是视频文件、幻灯片、文档等形式，而学校往往因为各类因素的限制，导游课程教学与实训难以与实际结合起来，学生与社会需求的人才普遍脱节，导致学生社会适应能力下降。

10%缺失率时，MICE填补后分析结果与列表删除分析结果相比，标准偏倚均低于40%，多元线性回归系数估计效果达到优良的均为3个，两种方法效果相当。

20%缺失率时，MICE填补后有1个系数标准偏倚低于20%，而此时列表删除法有2个系数满足优良的标准，两种方法的标准偏倚均未超过40%，说明此时MICE填补效果不如列表删除。

30%缺失率时，MICE填补后系数估计达优良的有1个，而列表删除为2个。但此时列表删除中存在标准偏倚超过40%的情况，说明在实际分析中缺失值可能导致该系数估计的偏差极大，甚至出现与原始完整数据分析结果相反的情况。

表3 MCAR多元线性回归分析回归系数偏倚情况

（2）随机缺失（表4）

10%缺失率时，MICE填补后所有系数标准偏倚均低于20%，表现优良，而此时列表删除标准偏倚低于20%的有2个，且有1个系数标准偏倚超过40%。说明此种情况下，MICE填补表现更好，列表删除效果欠佳。

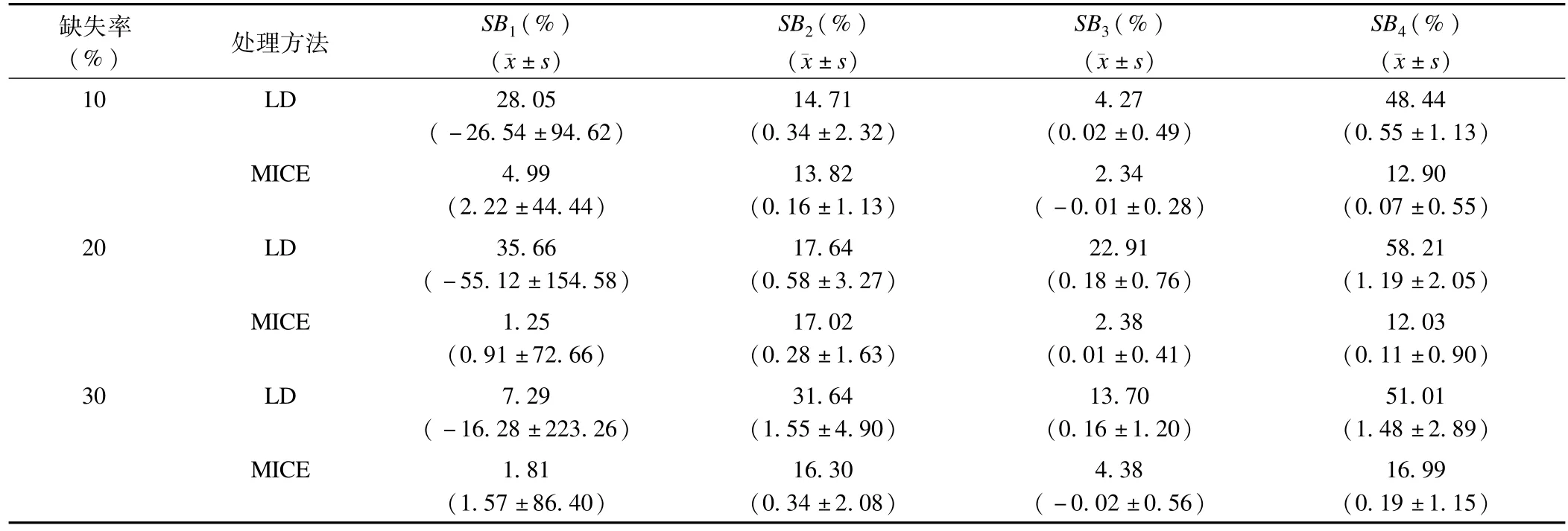
表4 MAR多元线性回归分析回归系数标准偏倚

20%缺失率时，MICE填补后估计回归系数表现优良，而此时列表删除偏倚很大，在实际应用中可能会使回归系数的估计产生极大的偏差。

30%缺失率时，MICE填补的效果依然表现优良，而列表删除后回归系数估计偏倚很大。

（3）非随机缺失（表5）

20%缺失率时，两种方法回归系数估计的标准偏倚中均有2个低于20%，2个超过40%，说明此时MICE填补和列表删除效果相当。

30%缺失率时，MICE填补后分析有2个回归系数标准偏倚低于20%，而列表删除只有1个低于20%，说明此种情况下MICE填补较列表删除效果好，但需要注意的是，此时两种方法处理后分析结果均有2个回归系数标准偏倚超过50%，回归系数估计很不稳定。

表5 NMAR多元线性回归分析回归系数标准偏倚

讨 论

在日常的统计分析中，如果没有对缺失值进行特别的处理，一般统计软件默认使用列表删除的方法进行分析，这无疑会丢失一部分的样本信息。本文着重对列表删除和MICE多重填补后分析结果进行比较。

本研究发现，对于MCAR资料，当缺失率不超过20%，在应用多元线性回归分析时，MICE多重填补相比列表删除并未表现出明显的优势；当缺失率达到30%时，列表删除可能会导致分析时产生异常结果，但总体而言此时MICE多重填补产生的偏倚较大。

MAR缺失的机制下，MICE多重填补后的分析结果相比列表删除的分析结果要好，即使在各种变量的缺失率都高达30%的情况下，MICE填补后多元线性回归系数标准偏倚依然不超过20%，表现稳健。

Van Buuren和Oudshoorn［14］认为MICE多重填补可用于NMAR的资料，但其应用效果却并不清楚。因此本次研究模拟了NMAR缺失，并进行MICE多重填补。本研究发现，非随机缺失下，在缺失率不超过20%时，MICE多重填补相比于列表删除表现不佳；当缺失率达到30%时，MICE多重填补优于列表删除，但此时MICE多重填补后也有半数回归系数标准偏倚超过50%，此时若应用MICE多重填补可能会导致分析结果明显偏离实际情况，甚至产生相反的结果。

对于分类变量，有时候研究者会关心该缺失值对应的真实数值是多少。通过计算不同缺失率、不同缺失类型下的错分率发现MICE多重填补后具有很高的错分率。

MICE填补的使用建议：

当缺失数据的缺失机制为随机缺失时，建议采用MICE多重填补。因为在单变量缺失率不超过30%的情况下，MICE填补后可以取得较好的分析效果。这也与Van Buuen［9］的模拟结果相符。当资料为完全随机缺失且各变量缺失率超过20%时，可以考虑采用MICE多重填补代替列表删除。当资料为非随机缺失时，不建议采用MICE多重填补处理缺失数据，且此时也不建议采用列表删除的方法处理，因为可能会产生不合理的研究结果。

对于缺失资料中的分类变量，不建议直接引用MICE多重填补以后产生的具体数值，这可能会产生严重的错误分类。

本研究主要关注MICE多重填补效果，故仅将MICE多重填补与列表删除进行比较，未将其他缺失数据处理方法纳入研究。部分缺失数据处理方法的比较已有一些相关研究，其研究结论可查阅相关文献［4，16，18-21］。

［1］Little RJ，D′Agostino R，Cohen ML，et al．The Prevention and Treatment of M issing Data in Clinical Trials．New England Journal of Medicine，2012，367（14）：1355-1360．

［2］Enders CK．Applied missing data analysis．Guilford Press，2010．

［3］李璐．基于R语言的缺失值填补方法．统计与决策，2012，（17）：72-74．

［4］刘鹏，雷蕾，张雪凤．缺失数据处理方法的比较研究．计算机科学，2004，（10）：155-156．

［5］帅平，李晓松，周晓华，等．缺失数据统计处理方法的研究进展．中国卫生统计，2013，30（1）：135-139．

［6］徐丽红，刘志永，刘桂芬，等．纵向监测连续非随机缺失数据变系数模型及其应用．中国卫生统计，2012，29（3）：314-317．

［7］季家超，王刚，张潇雅，等．数据非随机缺失机制的混合效应模式混合模型分析与应用．中国卫生统计，2013，30（2）：221-225．

［8］Lee KJ，Carlin JB．Multiple imputation for m issing data：fully conditional specification versus multivariate normal imputation．American journal of epidem iology，2010，171（5）：624-632．

［9］Van Buuren S，Brand JPL，Groothuis-Oudshoorn CGM，et al．Fully conditional specification in multivariate imputation．Journal of Statistical Computation and Simulation，2006，76（12）：1049-1064．

［10］Van Buuren S，Oudshoorn K．Flexible multivariate imputation by MICE．Leiden，The Netherlands：TNO Prevention Center，1999．

［11］Waljee AK，Mukherjee A，Singal AG，et al．Comparison of imputation methods for m issing laboratory data in medicine．BMJ open，2013，3（8）．

［12］Faris PD，GhaliW A，Brant R，et al．Multiple imputation versus data enhancement for dealing with m issing data in observational health care outcome analyses．Journal of Clinical Epidem iology，2002，55（2）：184-191．

［13］Kabacoff R．R in Action：Data Analysis and GraphicsW ith R．Greenw ich：Manning Publications Company，2011．

［14］Van Buuren G．m ice：Multivariate Imputation by Chained Equations in R．Journal of Statistical Software，2011，45（3）：1-67．

［15］Allison PD．M issng data techniques for structural equationmodeling．Journal of abnormal psychology，2003，122（4）：545-557．

［16］茅群霞．缺失值处理统计方法的模拟比较研究及应用．四川大学，2005．

［17］Collins LM，Schafer JL，Kam CM．A comparison of inclusive and restrictive strategies in modern m issing data procedures．Psychol Methods，2001，6（4）：330-351．

［18］赵俊康．不同缺失机制并存时偏倚校正的模拟研究．山西医科大学，2012．

［19］王曼，施念，花琳琳，等．成组删除法和多重填补法对随机缺失的二分类变量资料处理效果的比较．郑州大学学报（医学版），2012（5）：642-645．

［20］武建虎，贺佳，贺宪民，等．多变量缺失数据的不同处理方法及分析结果比较．第二军医大学学报，2004，（9）：1013-1016．

［21］张桥，李宁，张秋菊，等．任意缺失模式缺失数据不同填补方法效果比较．中国卫生统计，2013，30（5）：690-692．

（责任编辑：郭海强）

A Study on Effects of M ultivariate Im putation by Chained Equation Based on R Software

Zhang Tao，Zhu Lin，Ji Jiadong，etal．（DepartmentofEpidemiologyandHealthStatistics，SchoolofPublicHealth，ShandongU-niversity（250012））

ObjectiveTo evaluate the effects ofmultivariate imputation by chained equations（MICE）for datawith differentm issingmechanisms and variousm issing proportions，and explore the application situations of thismethod．MethodsA complete dataset from a cross-sectional study was used to simulatem issing datasetswith differentm issingmechanisms and variousm issing proportions by R software．The standard bias of the incomplete datasets obtained by listw ise deletion was compared with that of the imputed datasets obtained by MICE．Additionally，for binom ial variable，the average m isclassification ratio was calculated．ResultsMICE performed well for“m issing at random”data with the univariatemissing proportion of 10%，20% and 30%．In other scenarios，MICE failed to show advantage over listw ise deletion．For binom ial variable，the averagem isclassification ratiosweremore than 60%．ConclusionWhen the data wasmissing at random and the univariatem issing proportion was nomore than 30%，MICE was recommended to use，but the imputed value in binom ial variable was not suggested to be represented in raw data directly．

MICE；M issing data；Simulation；Multiple imputation

*：山东省科技发展计划（No．2014GGH218019）

△通信作者：李秀君，E-mail：xjli＠sdu．edu．cn