贝叶斯层次模型在嵌套结构调查数据中的应用研究*

重庆医科大学公共卫生与管理学院卫生统计学教研室（400016） 文 雯 文小焱 胡 珊 彭 斌

贝叶斯层次模型在嵌套结构调查数据中的应用研究*

重庆医科大学公共卫生与管理学院卫生统计学教研室（400016） 文 雯 文小焱 胡 珊 彭 斌△

目的针对分层抽样流行病调查数据的结构特点，构建两种基于分层嵌套思想的贝叶斯层次模型，并探讨其优缺点。方法以贝叶斯层次模型为基础，利用嵌套结构中的层级关系构建模型，其中，模型一以嵌套层效应分解为特点构建，模型二以嵌套层效应逐级传递为特点构建。以重庆市出生缺陷调查数据为例，采用OpenBUGS软件进行模型拟合及分析。结果以偏差信息准则（deviance information criterion，DIC）作为拟合优度评价，模型一和模型二的DIC值分别为101.8和101.6，大致相等；敏感性分析显示，在总体率的超参数μ设置不同先验信息下，模型一和模型二对总效应估计的变异性分别为（用标准差度量，10－4）：后验均数1.191和27.546；后验中位数1.038和7.617，模型一的变异性比模型二小。结论模型一和模型二均可用于嵌套结构的调查数据建模分析及预测，拟合效果相当；但模型一比模型二受先验信息影响小，稳健性更好，更适合先验信息欠缺时的数据分析。

嵌套结构数据 分层抽样 贝叶斯层次模型 OpenBUGS

随着马尔科夫链蒙特卡洛（Markov chain Monte carlo，MCMC）方法的不断成熟以及计算机软件的快速发展，贝叶斯统计方法被越来越多地用于科学研究和数据处理［1］。与经典统计方法不同，贝叶斯统计方法将未知参数看作随机变量，用一个概率分布去描述，称为先验分布。传统的统计方法应用样本信息和总体信息进行统计推断，而贝叶斯方法则利用样本信息、总体信息及先验信息进行统计推断［2］。当有先验信息可以利用时，采用贝叶斯方法可以得到更好的估计结果［3］。贝叶斯层次模型是在贝叶斯理论的基础上通过构造多层先验分布将模型以多层次的形式表现出来，即当参数的先验分布含有超参数时，对超参数再给出一个先验，称为超先验。由先验和超先验共同构建的层次先验作为模型的新先验，并采用贝叶斯统计推断方法对模型进行参数估计。这种方式构造的先验性质稳健，是社会科学研究领域广泛使用的建模方法之一［4－5］。嵌套结构是利用分层的思想将研究对象逐步划分成若干层，每一次划分都是建立在上一次分层的基础上，形成一层套一层类似蜂巢的结构。本文则是将这种思想应用于分层随机抽样调查数据的建模分析，利用多层贝叶斯统计方法，构建适应嵌套结构数据的层次贝叶斯模型，并探讨模型在该类型数据中的应用。

贝叶斯层次模型构建

1.抽样调查研究数据的嵌套结构特点

在抽样调查研究中，经常会选择分层随机抽样方法，即将调查总体（N）按其属性特征划分成若干层，然后在每个层中进行随机抽样。有时为了样本的代表性和实际需要，可进行多次分层，即在上一级分层基础上进行再分层，形成一层套一层的嵌套结构［6］。

2.构建贝叶斯层次模型

根据抽样调查研究数据的嵌套结构特点，对嵌套结构的每一层构建模型。下面以三层嵌套结构为例，阐述构建估计总体阳性率的贝叶斯层次模型的思路及具体方法。

模型一：基于广义线性模型的各嵌套层效应分解加成模型，简称效应分解加成模型。该模型以分层效应作为各嵌套层效应差别的主要原因，各嵌套层某分层单元的总效应等于其上一层总效应与该层分层效应之和。三层嵌套结构下各层所对应的效应模型分别为：

（1）～（4）式中，θ0表示总体阳性率，μ0为总体阳性率对应的平均效应；αi表示第一层第i分层单元的效应，且表示嵌套于第一层第i分层单元下第二层第j分层单元的效应，且γi（j（k））表示嵌套于第一层第i分层单元第二层第j分层单元下第三层第k分层单元的效应，且＝0。θi、θi（j）、θi（j（k））分别为相应嵌套层的总体阳性率。实际中，只需要拟合（4）式的模型即可估计出各层的参数。

模型参数的先验信息设定：μ0作为总体阳性率的平均效应，本文假设其服从均值为μ的正态分布，即μ0～norm（u，δ2）；α、β、γ作为各嵌套层的效应，可假设其服从均值为0的正态分布。

模型超参数设定：μ一般设定为正态分布或均匀分布，其均值可根据经验或文献资料确定；方差先验通常设置为逆伽玛分布（inverse gamma distribution）［7］，即方差的倒数（精度参数τ）服从伽玛分布τ～G（r，mu）。当没有方差先验信息可以利用时，通常需要将方差成分设置得足够大，例如106，精度系数趋于0，此时的（逆）伽玛分布就等价于一个无信息先验分布。

模型二：基于广义线性模型的各嵌套层效应逐级传递模型，简称效应逐级传递模型。该模型以各嵌套层效应仅受其上一层效应影响为出发点，各嵌套层间的嵌套关系通过层次先验来反映。前述三层嵌套结构对应的效应模型为：

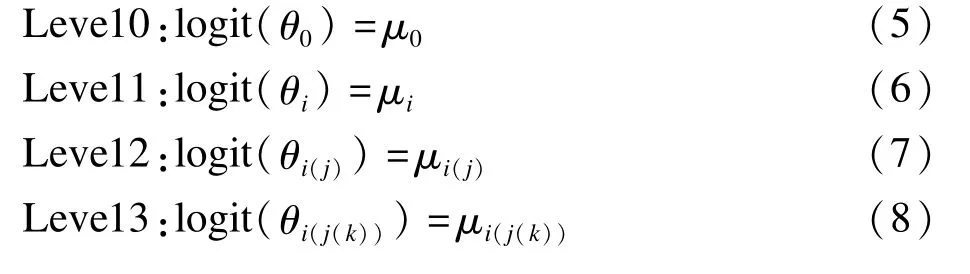
（5）～（8）式中，θ0、θi、θi（j）、θi（j（k））、μ0含义与模型一相同；μi为第一层第i分层单元的总效应；μi（j）为嵌套于第一层第i分层单元下第二层第j分层单元的总效应；μi（j（k））为嵌套于第一层第i分层单元第二层第j单元下第三层第k单元的总效应。

模型参数的先验信息设定：根据该模型构建思路，可假设每一嵌套层的效应服从以其上一级的效应为均值的正态分布［8］。即

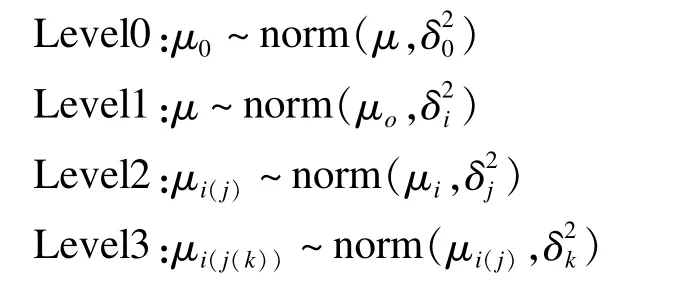
模型超参数设定：与模型一类似，可根据先验信息对超参数μ设定一个正态分布或均匀分布，方差均采用无信息先验分布。

实例分析

1.资料来源

数据来源于2010年重庆市0～5岁儿童出生缺陷基线调查。该研究采用多阶段分层随机抽样，第一阶段根据重庆市“一圈两翼”发展战略将全部40个区县划分为“一小时经济圈”、“渝东北翼”和“渝东南翼”三个经济区，第二阶段以区县为单位，按比例从三个经济区总共随机抽取16个区县作为调查点。

2.建立两层嵌套结构数据的贝叶斯层次模型

重庆市0～5岁儿童出生缺陷基线调查数据可视为两层嵌套结构的数据，即将重庆市（θ0）按照“一圈两翼”划分的三个经济区（θi）作为第一层嵌套，每个经济区按比例抽取出的区县（θi（j））作为第二层嵌套。设每个调查区县0～5岁儿童调查人数为ni（j），出生缺陷人数为xi（j），则可假设其服从二项分布，即

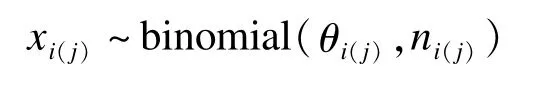
根据前面介绍的贝叶斯层次模型构建方法，对应的两类模型分别为：

模型一（效应分解加成模型）：

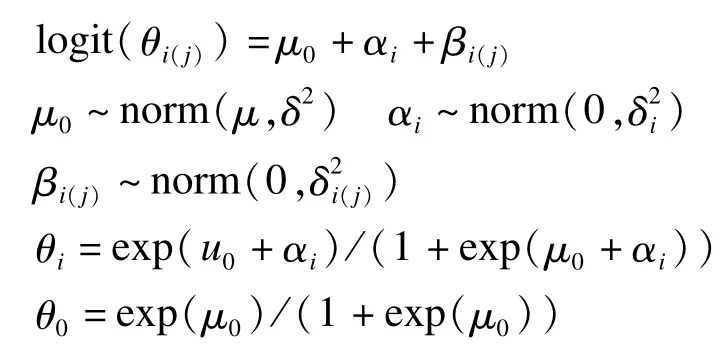
模型二（效应逐级传递模型）：

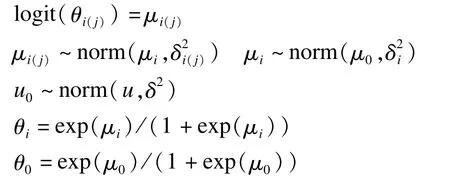
通过文献查阅，我国每年新增的先天残疾和智力缺陷儿童总数高达120万，约占每年出生人口的4%～6%［9－10］，鉴于重庆市历年来通过医院监测到的围产儿出生缺陷发生率均在1%左右［11－12］，而以医院为基础的监测方法由于研究对象受限以及筛查工作的不完善，统计出的出生缺陷发生率通常要比实际情况低。因此，本文认为总体出生缺陷发生率很可能介于1%～6%之间，其对应的u值范围为－4.595～－2.752（根据logit（θ）＝u推算），故可假设μ服从－4.595～－2.752之间的均匀分布，即μ～uniform（－4.595，－2.752）。方差先验采用逆伽玛分布，比较常用的设置有r＝mu＝0.001［13－14］或r＝mu＝1、r＝mu＝0.1、r＝mu＝0.01［15］或r＝0.5，mu＝0.005［16］，本文对以上设置进行了模拟研究，发现模型一和模型二在r＝mu＝0.01时相对较优。因此，本研究的方差先验采用τ～G（0.01，0.01）。

3.敏感性分析

敏感性分析是为了评估不同先验分布对模型后验的影响，即考察模型的稳健性（robustness）。当有可利用的先验信息时，敏感性分析主要考察先验分布的设置对模型后验的影响，当无信息先验被利用时，则主要考察不同无信息先验的选择对模型后验的影响［17］。鉴于本文所构建的模型中参数较多，且两种先验均有利用，因此本文选取对模型影响较大的超参数μ以及采用无信息先验的方差进行敏感性分析。

超参数μ在模型一和模型二中均表示总体效应μ0的先验均值，本文通过考查总体出生缺陷率θ0的先验信息将超参数μ设置如下五组先验范围：（1）通过经验和历史数据估计重庆市θ0的可能范围为1%～6%；（2）将（1）中设置的范围扩大到0.1%～20%，即理论上大多数地区出生缺陷发生率均在此范围；（3）设置一个与（1）无交叉，取值较小且包含于（2）中的范围：0.1%～1%；（4）设置一个与（1）无交叉，取值较大且包含于（2）中的范围：10%～20%；（5）设置一个无信息先验，即0%～100%。上述范围对应的超参数μ的先验分别为（1）μ～unif（－4.595，－2.752）（θ0介于1%～6%的均匀分布）；（2）μ～unif（－6.907，－1.386）（θ0介于0.1%～20%的均匀分布）；（3）μ～ unif（－6.907，－4.595）（θ0介于0.1%～1%的均匀分布）；（4）μ～unif（－2.197，－1.386）（θ0介于10%～20%的均匀分布）；（5）μ～unif（－10，10）（θ0介于0%～100%的均匀分布，即无信息均匀分布）。

将各种先验设置下参数的估计值与无信息先验下参数的估计值进行比较，以考察模型对超参数μ先验设置的稳健性。

4.模型拟合及诊断

所有模型均在OpenBUGS 3.2.2中运行，参数估计采用MCMC。平行模拟初始值不同的两条链，以克服不同初始值对模型的影响；采用Gelman-Rubin统计量目测各参数的迭代时序图，以评判模型是否收敛；模型稳定后迭代20000次用于参数估计和DIC的计算［17］。

5.结果及比较

（1）出生缺陷率的估计

以后验中位数作为出生缺陷率的点估计值，模型一和模型二的估计值分别为39.75‰和39.00‰，估计结果非常接近。模型一与模型二的DIC值分别为101.8和101.6，基本相等，说明两个模型拟合效果相当（表1）。此外，按照传统统计方法计算的出生缺陷率为37.92‰，模型一与模型二对全市出生缺陷率的估计值略高于传统统计方法的估计结果。

表1 出生缺陷发生率估计值（‰）及DIC值比较结果

（2）超参数μ不同先验的敏感性分析

由于模型一和模型二中参数较多，为了便于对比，本文仅选取了主要参数θ0的估计值（包括后验均值和后验中位数）进行呈现（表2）。与无信息先验相比，当先验设置为0.1%～1%时，模型一和模型二θ0估计值均较小，后验均数及后验中位数的差值（10－4）分别为－0.6和－0.5（模型一）、－25.2和－7.1（模型二）；当先验设置为10%～20%时，模型一和模型二θ0估计值均较大，差值（10－4）分别为2.4和2.1（模型一）、43.2和13.5（模型二）。从标准差这一角度看，模型一各先验设置对应参数θ0的后验均值和后验中位数标准差（10－4）分别为1.191和1.038，差别不大；模型二分别为27.546和7.617，差别较大，但后验中位数较后验均值更稳定。可以看出，两个模型后验估计值均在一定程度上受到先验信息的影响，但模型一在各种先验下的后验均值与后验中位数基本相等，且变异较小，模型表现稳健。模型二则受到不同先验设置的影响，参数估计值变异较大，欠稳定，尤其是后验均值受先验信息影响更明显。

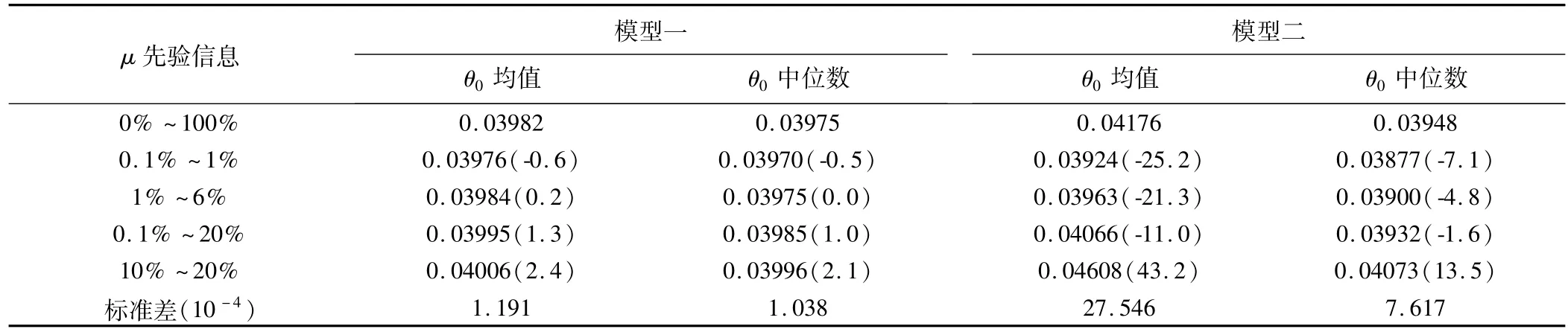
表2 超参数μ不同先验的敏感性分析结果

（3）方差先验的敏感性分析

对模型一和模型二采用前述5种方差先验进行拟合度的敏感性分析。结果显示（表3）五种方差先验信息下，模型一或模型二的DIC值相差均不明显。因此，模型一和模型二对方差先验表现稳健。考虑到先验IG（0.01，0.01）在两个模型中的DIC值均较小，故选择该先验作为模型拟合时的方差先验。

表3 五种方差先验下的模型DIC值

讨 论

在抽样调查研究中，采用分层随机抽样方法获取的数据具有一层套一层的嵌套结构特点。本研究通过分析数据的嵌套结构特点，构建了两个基于嵌套结构的贝叶斯层次模型：模型一（效应分解加成模型）和模型二（效应逐级传递模型），并利用重庆市出生缺陷调查数据，分析比较两个模型的优缺点。研究结果显示，模型一和模型二在拟合优度方面相差不大，模型二的DIC值略小于模型一，提示两个模型均能较好地拟合数据；稳健性方面，模型一具有较好的稳键性，模型二稳健性较差，尤其是后验均值极易受μ先验分布影响。另外，从模型的潜力看，模型一将各嵌套层的分层效应从该层总效应中分解出来，作为各嵌套层不同分层单元阳性率差异的主要原因，有利于探讨模型的内在结构及各层的效应贡献。在实例分析中，分层效应是由于区域间的地理位置差异造成，若是将地理位置细化（空间效应），或是考虑更多相关影响因素（如时间效应、经济效应等），将会提高模型预测的准确性［17］。模型二则是在各层的总效应水平上，通过构造各参数先验分布的嵌套关系进行模型构建，下一嵌套层的效应仅依赖于其上一层的效应，且通过逐级随机传递的方式进行影响，其独特的层次先验结构使模型得以简化的同时，失去了继续优化的可能。

关于超参数μ先验分布的选择，如果可以通过经验和文献资料收集到关于μ0充分的先验信息，则可利用这些信息确定μ值或其先验分布；若缺乏μ0的相关信息，则可根据研究具体情况选择一个合理范围的均匀分布或无信息先验。本文不建议在μ0无先验信息可利用的情况下对μ直接赋值0，即μ0～norm（0，δ2）这相当于将阳性率θ0默认设置为50%。由于模型一和模型二均受μ0先验的影响，尤其是模型二，这将会导致模型中主要参数估计过高。

综上所述，当有合理的先验信息（如合理的μ值范围）可利用时，模型一与模型二均能应用于嵌套结构数据建模分析及预测；但当先验信息不明确或欠缺时，考虑到模型二对先验信息过于敏感，选择模型一会更恰当，且模型一可通过细化分层效应以达到提高模型预测准确性的目的。

1.Smith AFM，Roberts GO.Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods.Journal of the Royal Statistical Society（Series B），1993，55（1）：3-23.

2.张尧庭，陈汉峰.贝叶斯统计推断.科学出版社，1991.

3.Tu XM，Kowalski J，Jia G.Bayesian analysis of prevalence with covariates using simulation based techniques：applications to HIV screening. Statistics in Medicine，1999，18（22）：3059-3073.

4.王哲.多层贝叶斯方法在消费者行为中的应用研究.南京：南京航空航天大学，2012.

5.Lindley DV，Smith AFM.Bayes estimates for the linear model.Journal of the Royal Statistical Society（Series B），1972，34（1）：1-41.

6.王建华.流行病学.北京：人民卫生出版社，2008.

7.Daniels MJ.A prior for the variance in hierarchical models.Canadian Journal of Statistics，1999，27（3）：567-578.

8.王显红.日本血吸虫病贝叶斯时空模型的建立.北京：中国疾病预防控制中心，2007.

9.毛萌，朱军.出生缺陷检测研究现状.实验儿科临床杂志，2009，24（11）：801-803.

10.李常惠，田宏，陈艳玲，等.辽宁省2011年度出生缺陷监测数据.中国卫生统计，2012，29（3）：410-411.

11.王继林，樊欣.重庆市1996－2001年出生缺陷监测结果分析.中国儿童保健杂志，2003，11（3）：207-209.

12.张高东，周文正，周晓军，等.重庆市2004－2010年出生缺陷发生情况分析.华中科技大学学报，2012，41（6）：759-762.

13.Su Z，Peterman RM，Haeseker SL.Spatial hierarchical Bayesian models for stock-recruitment analysis of pink salmon（Oncorhynchusgorbuscha）.Canadian Journal of Fisheries and Aquatic Sciences，2004，61（12）：2471-2486.

14.Kazembe LN，Namangale JJ.A Bayesian multinomial model to analyse spatial patterns of childhood co-morbidity in Malawi.European journal of Epidemiology，2007，22（8）：545-556.

15.Su Z，Adkison MD，Van Alen BW.A hierarchical Bayesian model for estimating historical salmon escapement and escapement timing.Canadian Journal of Fisheries and Aquatic Sciences，2001，58（8）：1648-1662.

16.Kelsall JE，Diggle PJ.Spatial variation in risk of disease：a nonparametric binary regression approach.Journal of the Royal Statistical Society（Series C），1998，47（4）：559-573.

17.Ntzoufras I.Bayesian modeling using WinBUGS.Wiley.com，2011.

18.张俊辉，冯子健，杨超，等.基于层次贝叶斯时空模型的空间多尺度联合分析模型的构建及应用研究.中国卫生统计，2013，30（2）：199-202.

（责任编辑：刘壮）

Application of Hierarchical Bayesian Model for Nested Structural Epidemiological Data

Wen Wen，Wen Xiaoyan，Hu Shan，et al.（Department of Health Statistics，School of Public Health and Management，Chongqing Medical University（400016），Chongqing）

ObjectiveTo develop two hierarchical Bayesian models for the epidemiological data with focusing on its nested structure；as well as to explore the pros and cons of them.MethodsRelationships among nested layers of nested structural data are taken into account when developing the two hierarchical Bayesian models.The first model focuses on the stratification effect of each nested layer for differentiation between the layers.The second model focuses on the transmission effect between the father layer and its son layers.Open BUGS software and a birth defects survey data were used to fit and evaluate the two hierarchical Bayesian models；and the deviance information criterion（DIC）was used for measuring the goodness-of-fit of them.A sensitivity analysis was conducted with different sets of prior information on hyper parameter of the population rateμ.ResultsThe DIC of the two models are 101.8 and 101.6，respectively，which shows almost the same goodness-of-fit of them.The sensitivity analysis shows that the standard deviation of the two models for the posterior mean of estimated population rate are（10－4）1.191and 27.546，respectively，for the posterior median of them are（10－4）1.038 and 7.617，respectively.Both results of posterior mean and posterior median say that the first model has smaller standard deviation under different prior information scenario.ConclusionBoth models can be used to model nested structural epidemiological data.However，the first model is affected by prior information much less than the second model does.Thus，the first model is more stable and is better to model nested structural survey data when little prior information is available.

Nested structural data；Stratified sampling；Hierarchical Bayesian model；OpenBUGS

国家自然科学基金（81373103）、重庆市科委基础与前沿研究计划项目（cstc2013jcyjA10009）

△通信作者：彭斌，Email：pengbin＠cqmu.edu.cn