新药临床研究中桥接试验的统计方法*

南京医科大学流行病与卫生统计学系（211166） 刘 晋 于 浩 柏建岭 曾 平 刘丽亚 陈 峰

新药临床研究中桥接试验的统计方法*

南京医科大学流行病与卫生统计学系（211166） 刘 晋 于 浩 柏建岭 曾 平 刘丽亚 陈 峰△

我国大部分新药仿制或进口自西方国家，它们的安全性和有效性在西方国家已得到确认，而这些由欧美人群建立的临床疗效和安全性结果是否可以直接外推到中国人群，是我国药物监管部门在审批此类药物时重点考虑的问题。针对外国引进药物，我国目前审批策略是：要求对引进的国外药品在我国人群中进行I-III期的临床试验，验证其对我国人群的安全性与有效性后方批准上市［1］。然而大量研究表明，大部分药品的药物特性在不同种族间类似。因此对所有申请上市药品无区别地进行重复试验常常造成时间延误及资源浪费［2－3］。

为解决此类问题，1998年美国、欧盟和日本三国组成的国际协调会议（international harmonization conference，ICH）发布了名为“种族因素对外国临床数据可接受性的影响”（ethnic factors in the acceptability of foreign clinical data）的指导文件（以下简称E5文件）［4］。该文件首次提出了桥接试验（bridging study）概念并建立了评价种族因素对药物疗效、安全性等影响的基本规范。在E5文件指导下，桥接试验策略在日本、台湾等国家和地区得到了推广、使用，许多新药在经过桥接试验后通过了药物监管部门的审批［5］。

目前在国内已发表文献中，除中国生物制品检定所桑国卫院士和南京医科大学辛卫权等对桥接试验的概念和国外应用进行了介绍外，尚未见到对桥接试验统计方法较为系统的介绍［1，6］。故本文将重点介绍桥接试验设计与分析中的统计方法，以期为我国临床试验研究者提供了解和引进这一国外新技术和新策略的借鉴和参考。

桥接试验的基本概念

ICH 1998年发布的E5文件指出，新药在原地域已经通过审批以后，如果要推广到新地域，可以利用原地域临床试验已有信息，按需在新地域进行小规模的附加试验研究，通过这些试验研究说明该药品对新地域人群具有同样的安全性、有效性，即可有效、快速地将原地域药品外推到新地域。因此，桥接试验只需证明药物在新地域安全性和有效性特征与原地域具有“相似性”（similarity）。而传统临床试验忽略原地域数据，仅依靠新地域数据证实药物在该地域的安全性与有效性。由于“相似性”往往涉及到桥接试验是否需要进行以及该试验是否成功或被认可，因此是桥接试验中一个极为重要的问题，但E5文件仅给出了“相似性”的概念，并没有给出判定相似性的标准和方法［7－9］。鉴于此，国外研究者围绕“相似性”问题进行了深入和广泛的探讨。现有研究从方法学上可分为经典统计方法（频率方法）和贝叶斯统计方法。从研究重点上看，则主要集中在“相似性”的度量、原地域信息的利用、现地域试验结果的模拟；在贝叶斯统计领域尚涉及结果的频率解释（I型误差和II型误差）以及与管理规范的衔接等。

桥接试验中的经典统计学方法

根据经典统计学原理，一些研究者从不同角度出发提出了桥接试验的频率统计方法。其中代表性的方法有以下三类：重建概率和概括概率法、加权Z检验法、两阶段设计和成组序贯设计法。

1.重建概率和概括概率法

Shao和Chow于2002年提出重建概率（reproducibility probability）和概括概率（generality probability）的概念［8－9，11］。所谓重建概率是指在新地域重复原地域试验结果的概率，当无明显证据表明两地域间的种族差异对药物疗效产生影响，通过计算重建概率判断是否需要进行桥接试验；而概括概率则为在已有信息表明新地域和原地域药物疗效可能存在差异的条件下，新地域得到疗效存在的概率。计算这两种概率的基本方法是利用原地域信息估计药物疗效的总体参数，进而计算在新地域I类错误控制在指定水准下的把握度。具体有三种计算方法：①估计把握度法（estimated power approach），②置信区间界值法（the confidence bound approach），③Bayes法（Bayesian approach）。随后，Chow提出以敏感性指标（sensitivity index）［11］作为药物疗效在两地域间变化的度量，并以该指标判断药物疗效能否在两地域间实现桥接。敏感性指标定义如下，令原地域疗效总体均值和标准差为uorginal、σorginal，令新地域效应总体均值和标准差分别为unew＝uorginal＋ε、σnew＝Cσorginal，其中ε和C分别为新地域疗效总体均值和标准差相对于原地域的改变量。则新地域疗效均值与标准差比值为：

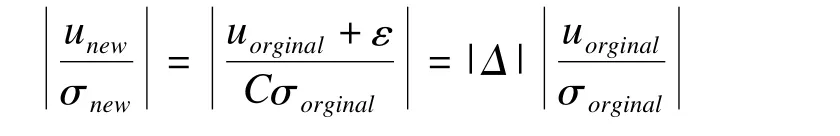
Chow等将Δ称为敏感性指标，Δ＝（1＋ε／uorginal）／C，该指标度量了两地域间疗效信噪比的改变量。在以下4种条件下：①ε和C都是固定常数；②ε为随机变量，C为常数；③ε为常数，C为随机变量；④两者都是随机变量；利用EM法可估计该敏感性指标。若该指标落于预定区域内，则判断桥接成功。但是这个区域该如何选择，作者并未给出明确建议。

2.加权Z检验法

2005年Lan首次提出加权Z检验（weighted z test）方法［12］。根据权重给定方式的不同，可以用于自适应设计的样本量再估计或应用于桥接试验的分析中。对于桥接试验中的加权Z检验，其基本思想是将原地域和新地域的近似正态性Z检验统计量（ZForeign，ZBridging），按照预先指定的权重（w）相加，得到新的统计量对Zw进行假设检验，若小于预定检验水准a，则认为桥接成功。权重w通过预先获得的关于原地域和新地域药物疗效的相似性在分析前确定。通过这种方式，新地域试验的检验水准αbridging被调整为αbridging＝1－φ（（zα－显而易见，αbridging受到权重w和原地域Z统计量两个因素的共同影响，往往会造成Ⅰ类错误膨胀，因此在应用此法时应注意Ⅰ类错误的大小应满足相关地域药物审批的法规要求。对于新地域的试验样本量估计，Lan指出可以通过对桥接地域的样本量相比较于原地域进行折扣的方式实现。令原地域试验的Ⅱ类错误为β，Ⅰ类错误为αFull，试验组与对照组疗效总体差值为Δ，则原地域每组所需总样本量为

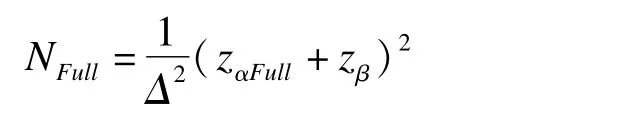
通过设定折扣因子D（discount factor），桥接地域的样本量：

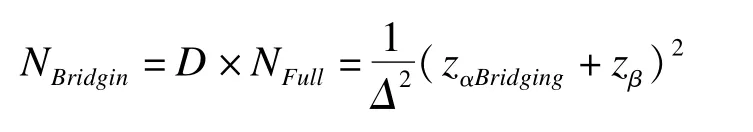
在保持桥接地域把握度不变的条件下，桥接地域所对应的Ⅰ类错误为

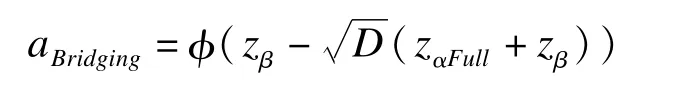
2012年Hsiao-Hui借鉴Lan加权Z检验思想，提出了另一种加权检验策略［13］。与Lan对Z统计量加权不同，他们通过对两地域总体疗效指标而非Z检验统计量进行加权，其定义的原假设为：

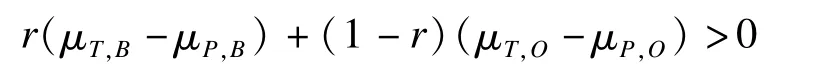
其中r为预先定义的权重，μT，B－μP，B，μT，O－μP，O分别为桥接地域和原地域试验组与对照组疗效差值。在此原假设下，对应的检验统计量服从t分布。在此基础上，Hsiao使用迭代方法求解出新地域所需样本量，并计算最大的权重取值。模拟试验显示，该迭代方法能够计算出将Ⅰ类、Ⅱ类错误控制在指定水准下所需最小的桥接地域样本量。

Xiaoyu Dong 2012年对Lan和Hsiao的方法进行了比较。考察在相同条件下，Ⅰ类、Ⅱ类错误以及样本量需求情况［14］。他认为Lan的方法中权重w的取值和两地域数据的变异度比值对Ⅰ类错误和把握度影响较大，而Hsiao的方法则相对稳定。

3.两阶段设计和成组序贯设计法

从另一角度出发，Hsiao xu和Liu将桥接试验视为在统一框架下分两阶段（原地域阶段和新地域阶段）进行的临床试验。在此基础上，将两阶段设计（two stage design）和成组序贯设计（group sequential design）引入桥接试验的设计与分析中［15－16］。该法的主要步骤为：第一阶段对原地域获得的试验结果进行t检验，若检验统计量T0大于预定界值C0则试验进入第二阶段（新地域试验），否则试验中止。当第二阶段（桥接阶段）完成后，对一、二阶段的累计数据进行最终分析。若检验统计量TN大于预定界值CN，认为可以将第一阶段原地域结果外推至第二阶段的新地域。在总Ⅰ类错误和Ⅱ类错误固定的条件下，采用两个参数r1和r2分配一阶段和二阶段的Ⅰ类和Ⅱ类错误。一阶段和二阶段Ⅰ类错误分别为

一阶段和二阶段Ⅱ类错误则分别为，

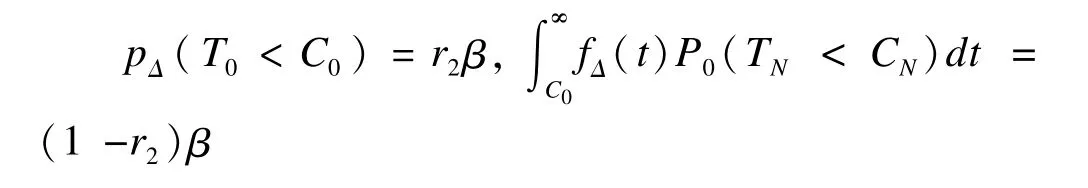
式中C0为一阶段的检验界值，CN为二阶段检验界值，τ为Ⅰ类错误调整参数。通过以上四个公式，即可得到原地域和新地域所需的样本量。

桥接试验中的贝叶斯统计方法

贝叶斯统计方法近年来日益受到重视，桥接试验通过合理使用已掌握的药物安全性、有效性信息（即原地域已上市药物的相关信息），支持药物在新地域的快速上市的思路和Bayes统计的理念十分契合。因此许多研究者对各种Bayes统计方法在桥接试验设计与分析中的应用进行了大量研究［17］。其代表性的方法有Bayes预测概率法、经验Bayes法、混合先验法、幂次先验法（power prior）和公度幂次先验法（commensurate power prior）。

1.贝叶斯预测概率法

Shih 2001年将原地域进行的试验（包括数个地区）视为多中心临床试验，将新地域视为一个新的中心，利用Bayes预测概率判断各地域间疗效的一致性（consistency）［7］。需要说明的是，Shih所说的一致性实际上是我们前面介绍频率方法时提到的相似性的另一种表达方式。假定原地域S个中心试验组和对照组比较t检验统计量为T＝（T1，T2，……，TS），令TN为新地域的t统计量，分别计算在给定T统计量条件下的TN和Ti的Bayes预测概率p（TN｜T）和p（Ti｜T）（i＝1，2，…，S）。若满足以下公式：

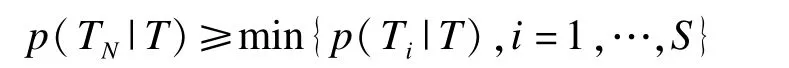
即在原地域所有试验中心数据基础上得到新地域观测数据的预测概率大于原地域任一中心的预测概率，则认为新地域与原地域间药物疗效具备一致性。此处预测概率是指在已有数据基础上，利用Bayes原理推断的未知数据各种取值的可能性。对于结果服从二项分布的数据，也可以按照上述方法的思路进行类似分析。该方法是E5文件发布后，首个被提出的桥接试验的Bayes方法。虽然它为以后的研究奠定了一定基础，但作为一种Bayes方法，Shih并没有评价监管机构十分关心的Ⅰ类、Ⅱ类错误，因此，该方法的统计特性值得进一步研究。

2.经验贝叶斯法

Liu等2002年将经验Bayes方法引入桥接试验的分析中，并利用总体参数后验概率构建相应的相似性判断标准［18］。具体方法为：将原地域试验组和对照组疗效差值作为新地域的先验，以桥接地域试验组和对照组疗效差值作为现有数据，利用经验Bayes方法计算新地域试验组与对照组疗效差值的后验概率，若两组疗效差值大于0的概率大于预定界值（1－α），则认为两地间疗效具有相似性。令μNT为新地域治疗组总体均值，μP为对照组总体均值，则新地域疗效的后验概率需满足下式：

PSI＝Pr｛μNT－μP＞0｜bridging data and prior｝＞1－α

式中α取值为试验前确定的，而新地域总体疗效μNT－μP大于0的近似概率（similary probability）PSI即可视为相似性的判断标准。

值得注意的是，该准则关注的是疗效的定性描述，即仅关注新地域试验组和对照组疗效差值是否大于0，而并不涉及其具体疗效大小。而在实际中即使新地域和原地域都有正向的疗效存在，但它们的疗效之间可能存在明显差别，因此，采用该判断方法可能并不能真正识别出两地域间疗效的相似性。为此Liu 2004年对其2002年的方法进行了改进，计算在整合新地域数据和原地域试验数据（bridging data and prior）条件下，新地域和原地域试验组疗效差值大于非劣效界值（δ）的概率（PSI）。并和事先确定的概率水平（1－α）进行比较，若大于（1－α）则认为药物在两地域疗效相似［19］。用公式表示为

PSI＝Pr｛μNT－μOT＞－δ｜bridging data and prior｝＞1－α

其中μNT为新地域治疗组疗效指标总体均值，μOT为原地域治疗组疗效指标总体均值。该方法原理与Liu（2002）方法类似。

Liu（2002）和Liu（2004）的相似性判断策略均直接以原地域的样本信息作为新地域的先验信息估计后验概率，而在实际工作中原地域数据样本量往往远大于新地域样本量，故在后验分布的计算中占据主导地位，常常使得新地域的结果无法“扭转”原地域结果，这就导致使用上述两种方法进行相似性判断时，即使新地域的疗效远低于原地域，最终也总是判断两地结果相似，而这正是经验Bayes方法的主要缺陷。

3.混合先验

针对经验Bayes法存在的缺陷，Liu 2007年在其2002年方法的基础上对先验信息的定义方式进行了改进，提出混合先验Bayes法（m ixture prior approach）以代替经验Bayes方法［20］。所谓混合先验是指总体参数的先验分布并非是单个分布函数，而是由两个分布函数按照一定权重相加组成。对于桥接试验而言，其中一个分布函数是由原地域已知的数据确定，而另一个分布函数则常常使用无信息先验分布，再将两者按照预定的权重相加，即得到混合先验分布。令总体参数为新地域试验组和对照组疗效之差：

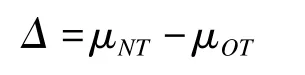
则混合先验分布形式为：

其中π1（ΔN）常为无信息先验，具体形式可以是均匀分布、方差较大的正态分布等；π2（ΔN）和前述经验Bayes先验相同，为根据原地域试验确定的经验先验。为预先指定的先验权重，取值范围。当γ为1时，不借用原地域信息，为0时，则退化为Liu（2002）方法中的先验。不难看出，混合先验通过权重调整有信息的原地域数据在整个先验信息中所占的比例，从而达到削弱原地域样本量过大造成的影响。然而，由于γ取值需要人为指定，加之其实际意义并不明确，因此在实际应用中很难给出其合理取值。

4.幂次先验法和公度幂次先验法

对于经验Bayes先验存在的原地域信息“掩盖”新地域信息问题，除了可以使用混合先验法外，也可以使用幂次先验（power prior）的方法加以解决。幂次先验通过指定幂次参数a0和初始先验（initial prior）将原地域信息以似然的形式纳入模型中，幂次a0的大小作为尺度参数用于调整历史信息被使用的程度，从而避免信息量较大的原地域数据掩盖可能的“真实”结果［21］。利用幂次先验法获得总体参数后验概率的一般过程如下：令现有试验数据为D，历史数据为D0，θ为感兴趣的总体参数，L（θ｜D）为似然函数；进一步，令π0（θ｜c0）为在历史数据D0被观测前关于θ的先验信息，称之为初始先验；则在给定幂次a0和历史数据D0的条件下，θ的幂次先验为：

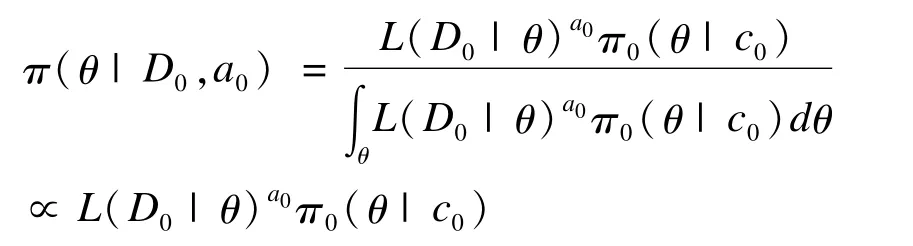
上式与一般Bayes公式的不同之处是其似然函数具有幂次a0，0＜a0＜1。当a0为1时，即利用全部原地域信息，退化为一般的层次Bayes先验；而a0为0时，则仅使用初始先验。在实际应用中，a0可以根据实际情况指定一个常数或为a0指定一个先验分布以反映a0取值的不确定性。显然，在桥接试验中我们可以在使用幂次先验得到新地域药物疗效指标后验概率后，进一步利用Liu 2002或2004年提出的相似性判断准则进行原地域和新地域的疗效相似性判断。Mihir Gandhi等于2012年采用这种方式对疗效指标服从二项分布的桥接试验数据进行了分析［22］。

在桥接试验数据分析中，幂次先验和混合先验两种Bayes先验指定方法都可以实现对原地域信息在合理范围内“有限度”的利用，然而幂次先验在许多条件下可给出直观解释，故幂次先验法更为实用。

虽然幂次先验可以方便直观地将原地域信息加以利用，然而，反映信息使用多少的幂次参数却需要人为指定，因此可能存在利用外部信息过多，超出合理范围的问题［23］。为解决此问题，Hobbs等在幂次先验方法的基础上提出了公度幂次先验（commensurate power prior）法［24］。该方法利用了幂次先验的基本原理，但通过增加一个度量两地域间总体参数相似性的参数τ，并估计其分布，自适应地确定a0的分布，从而避免了主观决定a0对结果产生的影响。具体过程为：

令θ0为原地域的疗效参数，对于θ0我们赋予其模糊先验或平坦先验，对于新地域数据θ的先验分布则由θ和度量θ和θ0相似性的参数τ决定。例如θ0的先验可以是θ～N（θ0，τ），其中方差τ的大小，即度量了θ和θ0相似性。在对τ指定一个模糊先验p（τ）后，即可得到关于（θ，θ0，a0，τ）的联合先验分布为

虽然该法需要估计更多的参数（比如τ），但是却改进了对a0的估计［24］。

讨 论

自1998年ICH E5指导文件发布以来，桥接试验设计和统计分析方法一直是国外临床试验研究的热点问题之一，现已初步形成了其特有的方法学体系（虽然远非完善）。如频率学派的成组序贯设计、加权Z检验、等效性检验、非劣效检验等。贝叶斯学派包括经验贝叶斯方法、贝叶斯预测概率、贝叶斯后验概率等。由于贝叶斯方法借助先验信息进行统计推断，因此和桥接试验的基本思想，即借用药物在原地域已获得的有效性、安全性信息支持其在新地域上市相吻合。因此贝叶斯方法在桥接试验上的应用较频率方法更为自然。目前的贝叶斯方法在桥接试验上应用的主要难点在于先验信息的确定或原地域已有信息的利用程度，以及利用贝叶斯后验概率进行决策时Ⅰ类错误的估计等。

目前针对桥接试验的统计设计分析方法较多，然而这些方法的优劣与特性的比较则相对缺乏。由于桥接试验本身特点，一些分析与设计方法并没有考虑Ⅰ类错误。而实际上桥接试验方法由于常常借助外来信息使得Ⅰ类错误膨胀，采用此种分析策略可能在一些国家或地区无法通过药物监管部门的审批。桥接试验的推广与应用离不开科学完善的统计设计与分析方法支撑，只有科学合理的对桥接试验结果进行分析与解释，才能发挥出这种试验策略的优势，这正需要我们统计工作者进行深入的探索与研究。

1.辛卫权，荀鹏程，于浩，等.新药临床试验中的桥接试验.中国临床药理学与治疗学，2008，13（3）：309-314.

2.Kihito T，Mari I，Hiromu N.Multiregional Clinical Trials for Global Simultaneous Drug Development in Japan，2012：235-250.

3.Mey W，Yeong-Liang L，Herng-Der C.Feasibility and Implementation of Bridging Studies in Taiwan，2012：251-264.

4.ICH.Triparite Guidance E5，Ethnic Factors in the Acceptability of Foreign Data.Federal Register，1998，83：31790-31796.

5.Christy C，Yoichi I，Norisuke K，et al.Design and Sample Size Considerations for Global Trials／／2012：121-150.

6.桑国卫.新药临床研究中的“桥接”试验.中国处方药，2003（2）：50-53.

7.Shih WJ.Clinical trials for drug registrations in Asian-Pacific countries：proposal for a new paradigm from a statistical perspective.Control Clin Trials，2001，22（4）：357-366.

8.Shao J，Chow S.Reproducibility probability in clinical trials.Statistics in Medicine，2002，21（12）：1727-1742.

9.Liu J，Chow S.Bridging studies in clinical development.Journal of biopharma ceutical statistics，2002，12（3）：359-367.

10.Khin N A，Yang P，Hung H，et al.Regulatory and Scientific Issues Regarding Use of Foreign Data in Support of New Drug Applications in the United States：An FDA Perspective.Clin.Pharmacol.Ther，2013，94（2）：230-242.

11.Chow SC，Shao J，Hu OY.Assessing sensitivity and sim ilarity in bridging studies.J Biopharm Stat，2002，12（3）：385-400.

12.Lan KK，Soo Y，Siu C，etal.The use of weighted Z-tests in medical research.J Biopharm Stat，2005，15（4）：625-639.

13.Tsou HH，Tsong Y，Liu J T，et al.Weighted evidence approach of bridging study.J Biopharm Stat，2012，22（5）：952-965.

14.Dong X，Guo Y，Tsong Y.A Note on Two Approaches of Testing Bridging Evidence to a New Region.Journal of Biopharmaceutical Statistics，2012，22（5）：966-976.

15.Hsiao C，Xu J，Liu J.A group sequential approach to evaluation of bridging studies.Journal of biopharmaceutical statistics，2003，13（4）：793-801.

16.Hsiao CF，Xu JZ，Liu JP.A two-stage design for bridging studies. JOURNAL OF BIOPHARMACEUTICAL STATISTICS，2005，15（1）：75-83.

17.Chin-Fu H，Hsiao-Hui T，Jen-pei L，et al.A Bayesian Approach for E-valuation of Bridging Studies，2012：89-104.

18.Liu J，Hsiao C，Hsueh H.Bayesian approach to evaluation of bridging studies.Journal of biopharmaceutical statistics，2002，12（3）：401-408.

19.Liu J，Hsueh H，Hsiao C.A Bayesian noninferiority approach to evaluation of bridging studies.Journal of biopharmaceutical statistics，2004，14（2）：291-300.

20.Hsiao CF，Hsu YY，Tsou HH，et al.Use of prior information for Bayesian evaluation of bridging studies.Journal of Biopharmaceutical Statistics，2007，17（1）：109-121.

21.Ibrahim JG，Chen M.Power prior distributions for regression models. Statistical Science，2000：46-60.

22.Gandhi M，Mukherjee B，Biswas D.A Bayesian apprroach for inference from a bridging study with binary outcomes.Journal of Biopharmaceutical Statistics，2012，22（5SI）：935-951.

23.Duan Y，Ye K，Smith EP.Evaluating water quality using power priors to incorporate historical information.Environmetrics，2006，17（1）：95-106.

24.Hobbs BP，Sargent DJ，Carlin BP.Commensurate priors for incorporating historical information in clinical trials using general and generalized linear models.Bayesian Analysis，2012，7（3）：639-674.

（责任编辑：郭海强）

*国家自然科学基金资助项目（81273184）；国家自然科学基金资助项目（81302512）

△通信作者：陈峰，E-mail：fengchen＠njmu.edu.cn