实数集中分形上函数的连续性

梁　莉，龙伦海，何　勇

(海南大学 信息科学技术学院，海南 海口 570228)



实数集中分形上函数的连续性

梁莉，龙伦海，何勇

(海南大学 信息科学技术学院，海南 海口 570228)

摘要：针对实数集R中一个紧的s-集E在欧氏拓扑下的完全不连通性，给出了E上实函数的在欧氏拓扑下的T-连续和Hausdorff测度下的Hspan-连续的定义、性质、运算及一些相关定理，对此建立了分形上一元函数的连续性理论.

关键词：s-集； Hausdorff 测度；T-连续；Hspan-连续

关于函数的非整数阶导数和非整数阶积分一直是分形几何的一个重要研究方向[1-3]，首先其定义就有很多种，也具有各种不同的结论，但最终的结果不甚理想，没有一个完善的理论体系.一元函数的微积分是数学分析和高等数学课程的主要研究内容，具有一套完善的理论体系[4]，其中最主要的连续、一阶导数和一重积分(包括不定积分和定积分)是建立在一维空间即实数集R上，因此可以在实数集R中一个非整数维紧的s-集E上建立一元函数的微积分理论体系.本文主要讨论实数集中一个紧的s-集E上函数的连续性理论，文中结果是研讨s-阶导数理论和s-阶积分理论的基础.下面首先给出一个固定的紧的s-集E上的函数在欧氏拓扑意义下的T-连续性的定义及性质.

1分形上函数的T-连续性

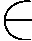
定义11) 称E中的最小点为E的左端点，最大点为E的右端点；

2) 如果E中的一个点存在该点的一个去心邻域与E的交为空集，则称该点为E的一个孤立点；

3) 如果E中的一个点满足该点的任何一个去心右邻域都与E的交非空，且存在该点的一个去心左邻域与E的交是空集，则称该点为E的一个右内端点；同样可定义E的左内端点；

4) 如果E中的一个点满足既不是E的左内端点，又不是E的右内端点，也不是E的孤立点，则称该点是E的一个内点.

根据该种分类法，E的左端点可能是孤立点，也可能是右内端点，同样右端点可能是孤立点，也可能是左内端点，除此之外的点只能是孤立点、左内端点、右内端点和内点之一.设x0是E的一个左内端点，根据定义E中的任何一个点x只能从x0的左边无限逼近于x0，若x0是右内端点，则x只能从x0的右边无限逼近于x0，而当x0是内点时,x就可以从x0的两边无限趋近于x0.

设f(E,x)是紧的s-集E上的一个以x为变量的一元实函数，当x0是E的左内端点，右内端点，内点之一，下面定义函数f(E,x) 在x0处的左T-极限、右T-极限和T-极限.

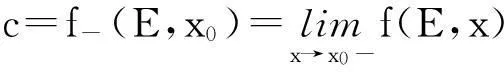
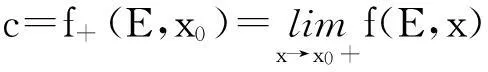
定义31) 设 x0是E的左内端点，在E中x0的右边如果存在离x0最近的点x1>x0，则称x1是x0的右邻点；

2) 设x0是E的右内端点，若存在E中x0的左边离x0最近的点x2

3) 设x0是E的孤立点，在E中x0的右边若存在离x0最近的点x1>x0，称x1是x0右邻点；同样可以定义x0的左邻点.

从定义3中可以看出E的左端点x0是孤立点时，就一定存在x0的右邻点，否则右邻点不存在；当右端点x0是孤立点时，就只存在x0的 左邻点，除此之外的点若是左内端点就只存在右邻点，右内端点就只存在左邻点，孤立点的左、右邻点都存在，内点的左、右邻点都不存在.为了表述当便，在存在的情况下，用x0-δ和x0+δ分别表示x0的左邻点和右邻点.

定义41) 设x0是E的左端点.如果当x0是孤立点时，有f(E,x0)=f(E,x0+δ) 成立，当x0是右内端点时，有f(E,x0)=f+(E,x0) 成立，则称函数f(E,x)在x0处是T-连续的;

2) 设x0是E的右端点.如果当x0是孤立点时，有f(E,x0)=f(E,x0-δ) 成立，当x0是左内端点时，有f(E,x0)=f-(E,x0)成立，则称函数f(E,x)在x0处T-连续;

3) 设x0是E的除左、右端点之外的点，如果当x0是孤立点时，有f(E,x0)=f(E,x0-δ)=f(E,x0+δ) 成立，当x0是右内端点时，有f(E,x0)=f+(E,x0)=f(E,x0-δ) 成立，当x0是左内端点时，有f(E,x0)=f-(E,x0)=f(E,x0+δ) 成立，当x0是内点时，有f(E,x0)=f-(E,x0)=f+(E,x0) 成立，则称函数f(E,x)在x0处具有T-连续性.

传统数学分析中函数的连续点要求在该点的左右极限与该点的函数值相等，但由于紧的s-集E往往是不连通的紧集，有无穷个点是左邻点或右邻点，当然也可能有孤立点，在其左邻点的右极限、右邻点的左极限及孤立点的左右极限都没有定义，从而无法在这些点处定义连续.为了规避这种缺陷，在定义中通过限制函数f(E,x)在点x0的函数值与其左右邻点(当存在时)的函数值都相等来加以弥补，从而得到这些点的连续性的定义.类似于分析的方法下面给出在E上整体的T-连续的定义.

定义5设f(E,x)是E上的实函数，若f(E,x)在E中的每一点处都是T-连续的，则称f(E,x)是E上的 T-连续函数.

由定义和紧的s-集E自身的特点，很容易得到E上的T-连续函数具有下列基本性质.

性质1 1) E上的T-连续函数不是单射，因此其反函数一定不存在；

2) 如果E中仅有有限个内点，则 E上的T-连续函数是常函数；

3) E上的常函数一定是 T-连续的，经典分析中除了常函数之外的所有其他初等函数限制在E上都不是 T-连续的；

4) 函数的加法、数乘、乘法、除法及复合运算在有意义的情况下都保持T-连续性不变.

传统分析中闭区间上的连续函数具有几个重要的性质，包括有界性、最值性、介值性和一致连续性，虽然E是紧集，但由于其在欧氏拓扑下的不连通性， E上的T-连续函数是否也具有类似的性质？回答是肯定的.下面就来讨论此问题.

定理1若f(E,x)是紧的s-集E上的T-连续实函数，则其值域一定是一个R中的有界闭区间.

由该构造和定义4，易证 g(x)为闭区间[a,b]上的连续函数，且g(x)和f(E,x)有相同的值域，事实上 g(x)是定义在[a,b]上且在E的每一个空格区间内及该空格区间的端点上都为常值的无穷级阶梯形连续函数.证毕

由定理1可直接得出推论1.

推论11) E上的 T-连续函数是有界函数；

2) E上的T-连续函数可以达到其最大和最小取值；

3) E上的T-连续函数可以能够取遍其最小取值和最大取值之间的所有数，即具有介值性，当然也有零点定理；

4) E上的 T-连续函数是一致连续的.

此处涉及到E上函数一致连续的定义问题，事实上只需在E上函数的所有连续内点(包括连续左内端点和右内端点)x0处的极限(包括左极限和右极限)的ε-δ 定义中，控制自变量x变化范围的δ只由ε确定，而与x0的选取无关来加以描述。

2s-紧集上函数的Hs-连续性

设E是实数集R中一个紧的s-集，现利用s-维Hausdorff测度对E中的点作如下分类.

定义61) 如果E中的一个点满足存在该点的一个去心邻域与E的交集的s-维Hausdorff测度为零，则称该点为E的一个Hs-孤立点；

2) 如果E中的一个点满足该点的任何一个去心右邻域都与E的交集s-维Hausdorff测度严格大于零，且存在该点的一个去心左邻域与 E的交集的s-维Hausdorff测度为零，则称该点为E的一个 Hs-右内端点；同样可定义E的Hs-左内端点；

3) 如果E中的一个点满足既不是E的Hs-左内端点，又不是E的Hs-右内端点，也不是E的一个 Hs-孤立点，则称该点是E的一个Hs-内点.

从定义6中可以看出，E 的Hs-右内端点仅在其右边的任意局部范围内都有正的s-维Hausdorff测度分布，Hs-左内端点仅在其左边的任意局部范围内才有正的s-维Hausdorff测度分布，而Hs-内点的左右两边任意局部范围内都有严格大于零的s-维Hausdorff夫测度分布，而对Hs-孤立点，则存在该点的一个局部邻域的s-维Hausdorff测度为零.因此利用定义1可以看出，E的孤立点一定是Hs-孤立点；E的 Hs-内点一定是E 的内点；而右内端点和左内端点都有可能变成Hs-孤立点.

下面给出E上函数f(E,x)的Hs-左极限、Hs-有极限和Hs-极限的定义.

3) 设x0是E的Hs- 内点，若存在一个实数c满足c=fHs-(E,x0)=fHs+(E,x0) ，则称c是f(E,x)在x0处的Hs-极限，记为c=fHs(E,x0).

下面定义 E上函数f(E,x)的Hs-连续性和Hs-一致连续性等概念.

定义81) 设x0是E中的任意点.当x0是E的Hs-左内端点时，有f(E,x0)=fHs-(E,x0)成立；当x0是E的Hs-右内端点时，有f(E,x0)=fHs+(E,x0)成立；当x0是E的Hs-内点时，有f(E,x0)=fHs-(E,x0)=fHs+(E,x0)；当x0是E的Hs-孤立点时，对任意的δ1,δ2>0，只要Hs(E∩[x0-δ1,x0+δ2])=0，就一定有f(E,x)在E∩[x0-δ1,x0+δ2]上取常数值， 则称函数f(E,x)在E上是Hs-连续函数；

2) 在Hs-连续的定义中，若还满足函数f(E,x)在x0处Hs-极限(包括左极限和右极限)的ε-δ定义中的δ只与ε有关，而与x0在E中作为Hs-内点或者Hs-内端点的选取无关，则称函数f(E,x)在E上是Hs-一致连续的.

根据定义8同样有E上的Hs-连续函数的四则运算和复合运算保持Hs-连续性不变，并且Hs-连续函数一定是Hs-一致连续的，另外由于E的Hs-内点和Hs-内端点一定分别是定义1的内点和内端点，反之则不然，因此不需加以证明的下述结论.

定理2 E上的Hs-连续函数一定是T-连续函数，反之则不成立.

1) 并集E1∪E2上的Hs2-连续函数在E1上只能取常值，因此E1∪E2和E2上具有相同的Hs2-连续函数；

下面给出Cantor三分集E上今后将要用到的一些具体Hs-连续函数的例子.

例3设f(u)是闭区间上的[0,Hs(E)]=[0,1]上的初等连续函数，称复合函数f(h(E,x)) 是分形集E上的初等函数，如(h(E,x))α,ch(E,x)(c>0), 分别称为Cantor集E上的幂函数，指数函数和余弦函数，同样有E上的初等函数是Hs-连续的.

3紧的s-集上Hs- 连续函数的扩张

命题1设E1,E2分别是紧的s1-集和s2-集，且E1⊆E2，则

1)E1上的T-连续函数在R上的扩张函数限制在E2上构成E2上的 T-连续函数；

2) 只有当s1=s2=s时，E1上的Hs-连续函数在R上的扩张函数限制在E2上构成E2上的Hs-连续函数.

该性质的结论缘于在E1⊆E2的条件下，E1中的内点一定是E2的内点，E1中的内端点一定是E2的内端点或内点；在E1⊆E2的条件下，只有当s1=s2=s时，E1中的Hs-内点才一定是E2的Hs-内点，E1中的内端点才一定是E2的Hs-内端点或Hs-内点，而当s1

参考文献：

[1]OldhamKB，SpanierJ.TheFractionalCalculus[M].NewYork:AcademicPress, 1974.

[2]LiangYS，SuWY.VonKochCurveanditsfractionalcalculus[J].ActaMathematicSinica,ChineseSeries, 2011, 54(2):227-240.

[3]TatomFB.Therelationshipbetweenfractionalcalculusandfractals[J].Fractals, 2011, 3(1):217-229.

[4]RudinW.PrinciplesofMathematicalAnanlysis[M].NewYork：McGraw-Hill, 1964.

[5]FalconerKJ.FractalGeometry—MathematicalFoundationsandApplications[M].NewYork：JohnWiley, 1990.

[6]LongLH.AnalgorithmoftheHausdorffmesureoftheFractalonthestraightline[J].ActaMathematicSinica,ChineseSeries, 2005, 48(1):11-16.

Continuity of Function on Fractal in Real Set

Liang Li, Long Lunhai, He Yong

(School of Information Science and Technology, Hainan University, Haikou 570228，China)

Abstract：Aimed at the complete unconnectedness of compacts-setEin real set, the definition, propriety, algorithm and some related theorems ofT-continuous andHspan-continuous by means of Euclidean topology and Hausdorff measure were proposed, and the continuity theory for the real function of one variable on fractal in R was established.

Keywords：compacts-set; Hausdorff measure;T-Continuous;Hspan-Continuous

中图分类号：O 174.12

文献标志码：ADOl：10.15886/j.cnki.hdxbzkb.2015.0019

文章编号：1004-1729(2015)02-0104-05

收稿日期：------------------------ 2014-10-10基金项目： 海南省自然科学基金项目(113003);海南大学2013年度校级教育教学研究项目(hdjy1331).

作者简介：梁莉( 1978 - ), 女, 四川内江人, 讲师.