三维音频空间参数感知熵的计算

章 佩，王晓晨，姜 林，2，张茂盛，2

（1.武汉大学计算机学院国家多媒体软件工程技术研究中心，武汉430072；2.武汉大学深圳研究院，广东 深圳 518063）

三维音频空间参数感知熵的计算

章 佩1，王晓晨1，姜 林1，2，张茂盛1，2

（1.武汉大学计算机学院国家多媒体软件工程技术研究中心，武汉430072；2.武汉大学深圳研究院，广东 深圳 518063）

空间参数感知熵的计算源自空间参数生理感知模型，该模型由耳蜗频率位置映射模块、延时衰减网络模块和噪音叠加模块组成。但延时衰减网络和噪音叠加模块各自对人耳分辨率的影响难以定量描述，并在计算空间参数感知熵时混淆了空间参数量化误差和量化步长的概念。针对以上问题，提出空间参数感知模型，采用空间参数生成模块和人耳分辨率模块替代延时衰减网络模块和噪音叠加模块，添加感知幅度压缩模块，并分析空间参数最大量化误差与量化步长之间的关系，给出空间参数感知熵计算公式。实验结果表明，与现有空间参数感知熵计算方法相比，该方法更全面地考虑到了空间参数的冗余，在相同的音频序列下，空间参数感知熵更小。

空间参数；感知；熵；量化；音频序列

DO I：10.3969/j.issn.1000-3428.2015.10.048

1 概述

随着多媒体技术的发展，传统的立体声已经不能满足人们对声音的要求，相较于传统立体声，三维音频因其声道数目的增多能提供更好的沉浸感和空间方位感，然而声道数目激增带来的海量数据给三维音频的传输和存储技术带来了挑战，以日本UHDTV国家标准的伴音标准中规定的22.2多声道三维音频系统为例，未经压缩码率就达到28 M b/s，一小时节目的数据量近100 GB，对存储介质和传输信道的要求大幅提升，制约了三维音频技术的发展和推广应用，因此，三维音频压缩编码技术成为当前多媒体技术之一。

在空间参数生理感知模型（Binaural Cue Physiologcal Processing Model，BCPPM）中，延时衰减网络和噪音叠加对人耳分辨率影响机理还在探求当中，缺乏相应的计算公式和模型，难以用于空间参数感知熵的计算；并在计算空间感知熵时混淆了空间参数的量

化误差和量化步长之间的关系。因此，本文提出一种空间参数感知模型（Spatial Parameter Perceptual Model，SPPM），并基于此模型建立空间参数最大量化误差与量化步长之间的关系，给出空间参数的感知熵公式。

2 背景介绍

文献［2］在文献［1］提出的“熵增定律”基础上提出了信息熵的概念，并将其作为信息的度量，指出了信源无损压缩的下限，此外还给出了率失真这一重要概念，即在给定的失真度量和相应的失真上下限值的条下，最少可以用多少比特表示信号。20世纪70年代的心理声学模型解释了人耳听觉感知的原理［3-4］，文献［5］结合心理声学提出了单耳听音模型（Monaural Hearing Model，MHM）和感知熵（Perceptual Entropy，PE），给出了感知无失真前提下音频信号压缩的理论极限的量度方法，例如，MP3［6］和AAC［7］在感知熵的指导下取得了较高的压缩率，并得到了广泛应用。90年代后，立体声和多声道音乐因其更佳的沉浸感受和听觉体验成为主流，面向单声道的编码技术在对多声道信号编码时编码码率会随着声道数的增加而线性增长，导致存储、传输成本大幅增加，为此声道间冗余去除技术成为研究热点。DTS、杜比公司提出了和差技术、强度立体声技术来去除声道间信号冗余［8-9］。文献［10-11］提出了空间参数编码（Binaural Cue Coding，BCC），指出立体声信号在单声道信号基础上引入了空间信息［12-13］。基于此提出的空间音频编码技术于2004年成为ISO/MPEG立体声和多声道的编码标准。但传统空间音频编码技术仅从去除空间信息的客观冗余出发，对声音空间信息主观感知特性考虑和利用不充分，空间信息的压缩效率还有待提高。武汉大学陈水仙博士借鉴Johnston计算感知熵的单耳听音模型（Monaural Hearing Model，MHM）的建模思想［2］，根据空间参数的敏感特性提出了BCPPM模型，并在BCPPM模型的基础上进一步给出空间感知熵计算公式，用来度量空间参数的感知信息量［14］。人类听觉系统能够根据空间参数判断声源的方位，但其分辨率有限，在空间参数值发生变化时，只有当其变化量达到或超过最小阈值（Just Notice Difference，JND），即人耳分辨率，才能察觉到这种变化，换句话说，若误差在感知阈值之下则不会影响主观听音感受［15］。

3 基于SPPM模型的空间参数感知熵计算

3.1 SPPM模型构建

SPPM模型由耳蜗频率位置映射模块、空间参数生成模块、有限分辨率模块和感知幅度压缩模块4个部分组成。声源信号经过不同的路径到达人耳，将获得的声信号通过耳蜗频率位置映射模块按频带划分进行处理；经空间参数生成模块使人耳接受到声源位置的空间线索，主要由双耳强度差（Interaural Level Differences，ILD）、双耳时间差（Interaural Tim e Differences，ITD）以及双耳相关度（Interaural Coherence，IC）表达。由于人类听觉系统灵敏度具有一定的局限性，导致人耳接受到信号的分辨率是有限的，人耳分辨率一般通过主观听音实验测得，仅获得感知到的空间参数部分，即空间参数的有效感知量；最后通过感知幅度压缩模块输出空间参数感知熵［16］，如图1所示。

图1 空间参数感知模型

3.2 空间参数的感知熵计算

空间参数的感知熵给出了无感知失真前提下理论压缩极限的量度方法，可用于计算编码时所需比特数下限。空间参数感知熵的计算模型如图2所示，主要包括临界频带划分单元（对应耳蜗频率位置映射模块）和空间参数计算单元（对应空间参数生成模块）、有效感知量计算单元（对应有限分辨率模块）、空间参数感知熵计算单元（对应感知幅度压缩模块）。

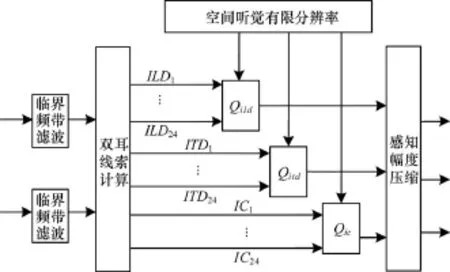
图2 空间参数感知熵的计算模型

3.2.1 临界频带划分单元

人的听觉系统可看成是一组多通道带通滤波器，经过该多通道滤波器组的音频信号被滤波成子带信号，每个子带对应于耳膜特定的物理位置，在频域掩蔽曲线中，掩蔽阈值在以掩蔽信号频率为中心的一个频带内为常数，这个频带的带宽称为以该信号频率为中心的临界频带（Critical Band，CB）。本文采用快速傅里叶转换（Fast Fourier Transform，FFT）模拟人耳频率位置映射模块进行临界频带划分，FFT变换长度取2 048点，有50%的重叠，临界频带数据采用Scharf的临界子带划分［3］。

3.2.2 空间参数计算单元

声信号经过空间参数生成模块后，获得人耳定位的空间参数。

根据FFT变换的能量守恒性质，时域信号的能量比与FFT谱线的能量比等价。计算式如下：

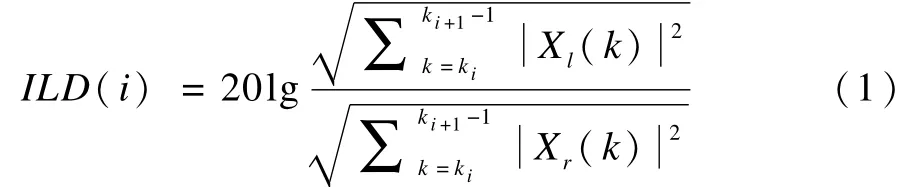
其中，i是临界频带标号；ki和ki+1分别是临界频带i和i+1的起始FFT谱线标号；Xl（k）和Xr（k）分别表示左右声道第k条FFT谱线的能量。

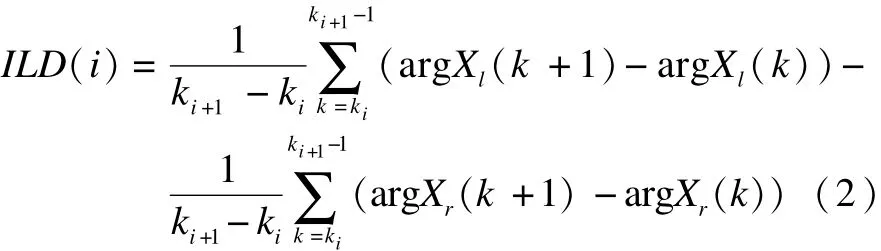
由于时域延时对应FFT域的线性相移，时域信号的延时差ITD与FFT谱线的群延时差等价。因此，ITD计算式如下：其中，arg取相角；音频信号在时域只考虑实部，时域信号的归一化相关度与FFT谱线的子带归一化相关度的实部等价。因此，IC计算式如下：

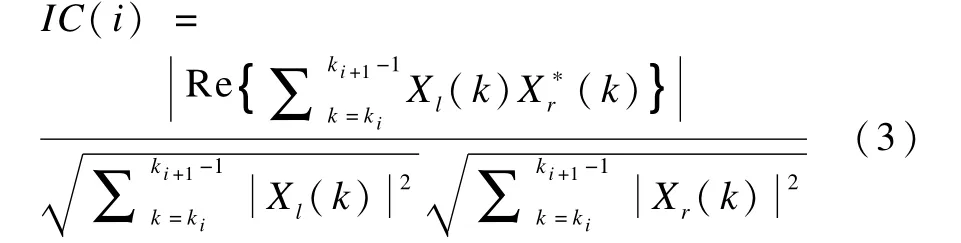
其中，*表示共轭。

3.2.3 空间参数有效感知量计算单元

空间听觉有限分辨率单元，如图2所示，是计算有效感知量的关键部分，设在一个临界带中空间参数值为Pspatial，量化值为P’spatial，量化误差为ε，由此可得：

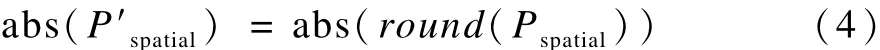
由式（4）可得：

设空间参数的量化步长为 δ，由式（4）和式（5）得：

其中，abs表示取绝对值；round表示四舍五入取整，在对空间参数进行量化时，给出一个量化步长，使得空间参数的量化误差控制在人耳感知的范围内，能有效降低空间参数失真出现的可能性，从而提高音质。

下面以ILD为例，讨论ILD的信息量，ILD临界频带的量化步长计算。

设第i个临界频带对应的ILD的JND为ResolL（i），量化步长为δILD，在对空间参数进行量化时，给出的量化步长使得空间参数的最大量化误差与每个频带对应的JND相等，根据式（6）可得：

由式（7）得：

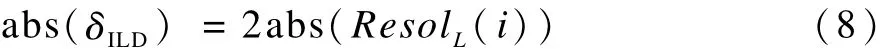
ILD每个临界频带受人耳分辨率的影响其有效感知量的计算式为：

将式（8）代入到式（9）中可得到：

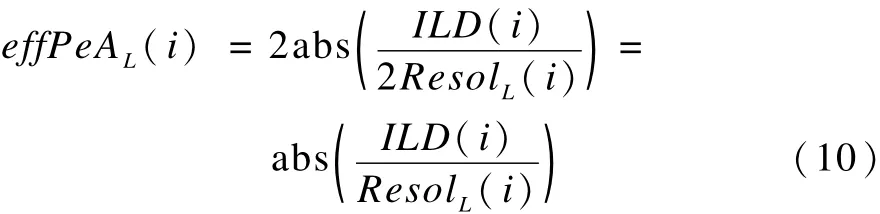
设每个子带量化的比特数为 QuaBit（i），当effPeAL（i）=0时，QuaBit（i）=0；当effPeAL（i）≠0时，有：

则ILD整个频带所需要的比特数为：

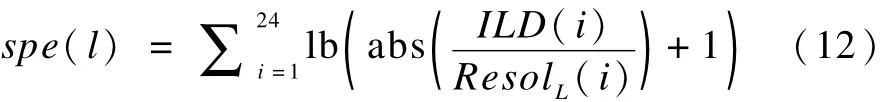
3.2.4 空间感知熵计算单元

ILD的有效感知量进入感知幅度压缩单元，完成ILD空间感知信息的输出，则ILD整个频带的感知熵为：

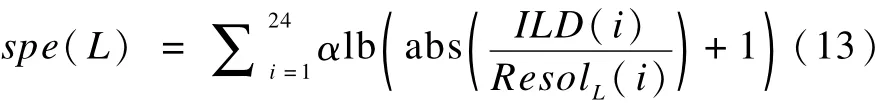
同理可得ITD整个频带的感知熵为：

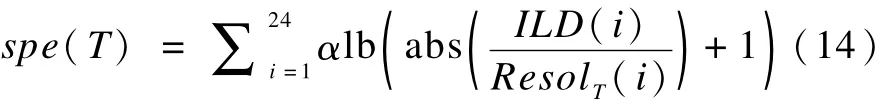
IC整个频带的感知熵为：

其中，ILD（i），ITD（i），IC（i）分别由式（1）～式（3）给出；ResolT（i）表示第i个临界频带对应ITD的JND；ResolC（i）表示第i个临界频带对应IC的JND；α是听觉感知的幅度压缩因子，一般取

0.6 ［16］。

4 实验与结果分析

目前测量空间参数的JND值都是针对一些特定点进行定性的描述，且JND值越小灵敏度越强，定位性越好，武汉大学王恒博士依据人耳的感知特性，将音频信号划分成24个子带，频率覆盖范围20 Hz～15 500 Hz，采用经典心理声学中1 up/2 down心理测试方法，模拟人的认知过程，逐步逼近目标测试值，获得全频带的JND值，此方法更能揭示空间参数JND的变化规律，测量出的结果相较其他测量方法更加精细［17］。本实验从3GPP标准中选用44.1 kHz采样率下的单声源、多声源2种不同类型的立体声序列作为测试序列，共计24个序列，如表1和表2所示。

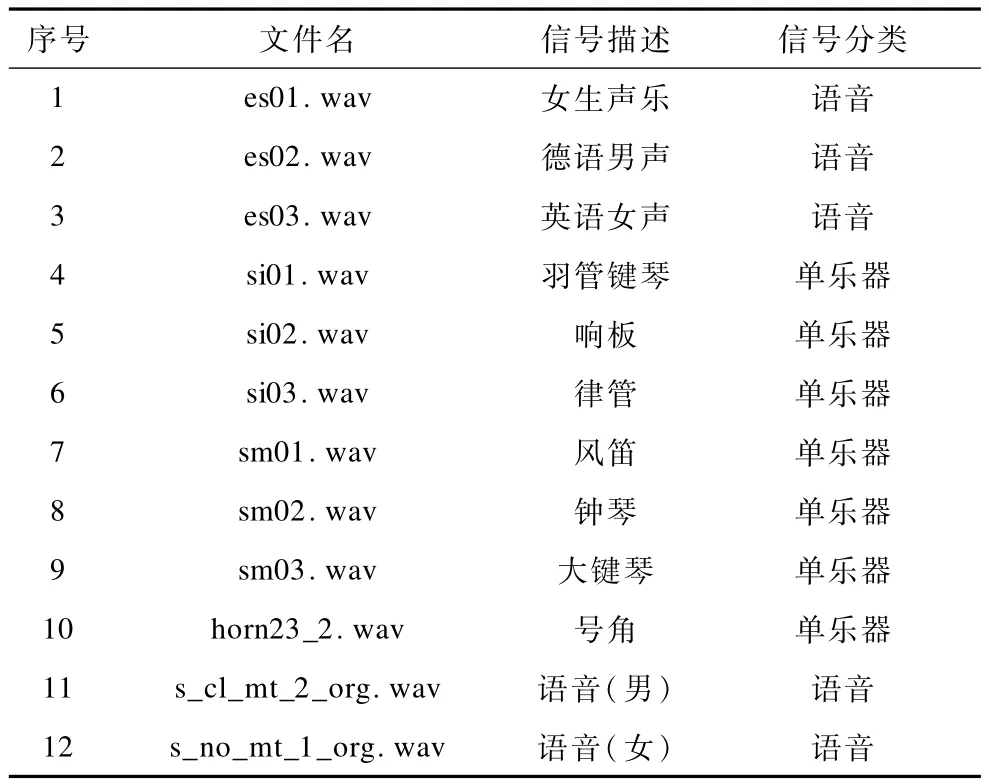
表1 单声源数据

表2 多声源数据

以ILD为例并结合王博士测量的ILD的JND数据，如图3所示，计算其感知熵，对比分析［14］计算空间参数感知熵的估量方法，为了便于比较，将空间参数的感知熵用一个统计平均量进行表示，记录编码时每秒至少需要使用的比特数，其中N-spe表示本文提出的空间参数感知熵估量方法的值，O-spe表示文献［14］中提出的空间参数感知熵估量方法的值，N-Aspe表示本文提出的空间参数平均感知熵估量的值，O-Aspe表示文献［14］中提出的空间参数平均感知熵估量的值。

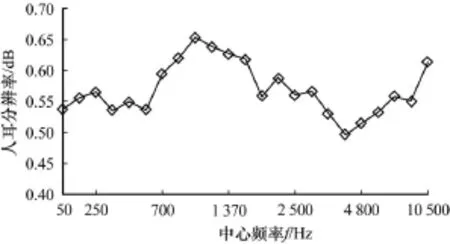
图3 ILD的JND随中心频率变化曲线

从图4和图5可以看出，本文在BPPM模型下对空间参数进行感知熵估算时所需要的比特数比BCPPM模型少，是因为本文通过建立量化步长和JND之间的关系，使得计算结果更加接近实际值。另外，从图6可以看出，单声源序列ILD的感知熵的平均值比多声源序列低，究其原因是测试用的单声源序列一般是空间信息量较少，而多声源由于融合多种声源，声道差异较大，因此声源信息较复杂，空间信息量相对较多。

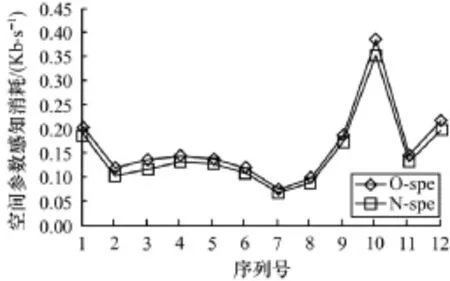
图4 单声源序列ILD的感知熵对比

图5 多声源序列ILD的感知熵对比

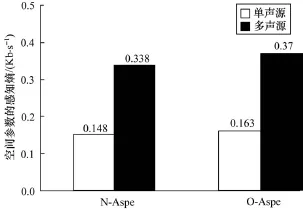
图6 单声源和多声源ILD的平均感知熵

5 结束语

本文针对BCPPM模型的问题，提出了BPPM模型，并给出基于BPPM模型的空间参数感知熵算法。通过分析量化步长和JND之间的关系，描述空间参数可感知信息量的计算方法，推出了空间参数感知熵的公式。从推算的空间参数的感知熵公式可知，空间参数的感知熵公式主要跟空间参数本身以及JND值有关，空间感知熵随着JND值变大而变小。下一步工作的目标是利用空间参数感知熵指导三维音频空间参数的感知编码。

［1］ Clausius R.On a Mechanical Theorem Applicable to Heat［J］.Philosophical Magazine，1870，40（4）：122-127.

［2］ Shannon C E.The Mathematical Theory of Communication［M］.Chicago，USA：University of Illinois，1949.

［3］ Scharf B.Complex Sounds and Critical Bands［J］. Psychological Bulletin，1961，58（3）：205-217.

［4］ Hellman R P.Asymmetry of Masking Between Noise and Tone［J］.Perception&Psychophysics，1972，11（3）：241-246.

［5］ Johnston JD.Transform Coding of Audio Signals Using Perceptual Noise Criteria［J］.IEEE Journal on Selected Areas in Communications，1988，6（2）：314-323.

［6］ Chiariglione L.MPEG：A Technological Basis for Multimedia Applications［J］.IEEE Multimedia，1995，2（1）：85-89.

［7］ Bosi M，Brandenburg K，Quackenbush S.ISO/IEC MPEG-2 Advanced Audio Aoding［J］.Journal of the Audio Engineering Society，1997，45（10）：789-814.

［8］ Johnston J，Ferreira A.Sum-difference Stereo Transform Coding［C］//Proceedings of IEEE International Conference on Acoustics，Speech，Signal Processing. Washington D.C.，USA：IEEE Press，1992：569-572.

［9］ Herre J，Brandenburg K，Lederer D.Intensity Stereo Coding［C］//Proceedings of the 96 th Audio Engineering Society Convention.New York，USA：AES Publications，1994：37-99.

［10］ Faller C，Baumgarte F.Binaural Cue Coding：A Novel and Efficient Representation of Spatial Audio［C］// Proceedings of IEEE International Conference on Acoustics，Speech，Signal Processing.Washington D.C.，USA：IEEE Press，2002：1841-1844.

［11］ Faller C，Baumgarte F.Binaural Cue Coding-Part II：Schemes and Applications［J］.IEEE Transactions on Speech and Audio Processing，2003，11（6）：520-531.

［12］ Blauert J.Evaluation Nonidentical Ear Input Signals［M］.Cambridge，USA：MIT Press，1983.

［13］ Roffler K，Butler A.Factors That Influence the Localization of Sound in the Vertical Plane［J］.Journal of Acoustical Society of America，1968，43（2）：1255-1259.

［14］ Shuixian C，Ruimin H，Naixue X.A Multimedia Application：Spatial Perceptual Entropy of Multichannel Audio Signals［J］.EURASIP Journal on Wireless Communications and Networking，2010，210（1）：27-41.

［15］ Blauert J.Spatial Hearing：The Psychophysics of Human sound Localization［M］.Cam bridge，USA：M IT Press，1997.

［16］ Princen J，Bradley A.Analysis/Synthesis Filter Bank Design Based on Time Domain Aliasing Cancellation［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1986，34（5）：1153-1161.

［17］ 王 恒.三维音频中空间线索感知特性研究［D］.武汉：武汉大学，2013.

编辑 顾逸斐

Calculation of 3D Audio Spatial Parameters Perception Entropy

ZHANG Pei1，WANG Xiaochen1，JIANG Lin1，2，ZHANG Maosheng1，2

（1.National Engineering Research Center for Multimedia Software，Computer College，Wuhan University，Wuhan 430072，China；2.Shenzhen Research Institute，Wuhan University，Shenzhen 518063，China）

The calculation of spatial parameters perception entropy is currently based on the Binaural Cue Physiologcal Processing Model（BCPPM），which consists of frequency-to-place transform in cochlear，delay-attenuation network and effective channel noises.However，the frequency-to-place transform in cochlea and the delay-attenuation network is difficult to quantitatively describe.In addition，the difference between the quantization error of spatial parameters and the quantization step of spatial parameters is confused in computing spatial parameters perception entropy.This paper proposes a new Spatial Parameter Perceptual Model（SPPM）to address these problems in BCPPM.The delay-attenuation network module and the effective channel noises module are replaced with the spatial parameters generation module and the JND module，and a perception amplitude compression module is added.Besides，it also analyzes the relationship between maximum quantization error of spatial parameters and the quantization step of spatial parameters，then gives a space parameter perceptual entropy formula based on SPPM.Since the spatial redundancy parameters are taken full consideration，experimental results confirm that spatial parameters perceptual entropy is smaller in the proposed method than the spatial parameters perceptual entropy based on BCPPM.

spatial parameter；perception；entropy；quantization；audio sequence

章 佩，王晓晨，姜 林，等.三维音频空间参数感知熵的计算［J］.计算机工程，2015，41（10）：255-259.

英文引用格式：Zhang Pei，Wang Xiaochen，Jiang Lin，et al.Calculation of 3D Audio Spatial Parameters Perception Entropy［J］.Computer Engineering，2015，41（10）：255-259.

1000-3428（2015）10-0255-05

A

TP37

国家自然科学基金资助项目（61231015，61201169，61201340）；深圳市科技计划基金资助项目（ZDSYS20140509165757632）。

章 佩（1988-），女，硕士研究生，主研方向：参数感知编码；王晓晨，讲师、博士；姜 林、张茂盛，副教授、博士。

2014-10-28

2014-11-26E-m ail：m isszhangpei@163.com