基于Student-t分布的混合模型图像分割方法

牛艺蓉，王士同

（江南大学数字媒体学院，江苏 无锡 214122）

基于Student-t分布的混合模型图像分割方法

牛艺蓉，王士同

（江南大学数字媒体学院，江苏 无锡 214122）

传统图像分割方法在分割被重尾噪声污染的图像时的分割效果不理想。针对该问题，提出一种基于Student-t分布的图像分割方法。该方法根据像素间的空间关系，计算出其先验概率，使用梯度下降法优化参数，从而最小化误差函数，在参数优化后得到像素点的后验概率值，对像素进行标记以实现图像分割。实验结果表明，在处理被重尾噪声腐蚀的图像时，与传统的K-均值、模糊C-均值等图像分割方法相比，该方法的误分率较低，分割效果较好。

Student-t分布；重尾噪声；图像分割；空间邻域关系；高斯混合模型

DO I：10.3969/j.issn.1000-3428.2015.10.038

1 概述

图像分割作为计算机视觉和图像处理中的一个基本并且重要的研究技术，是图像分析前经常使用的一个重要步骤，为图像理解、识别等高层图像操作打下坚实基础。图像分割根据图像的某些特性把图像中有意义的事物从背景中分割出来。正确的分割结果能够为信息判断提供有力的依据。然而图像很容易受到噪声的影响，这就给图像分割带来一定的难度。

近年来，聚类方法已经成为图像分割研究中的一个热点。有限混合模型（Finite Mixture Model，FMM）［1-3］作为一种聚类模型，它提供了一种灵活的方式对各种随机现象进行建模。当它的成员函数是高斯分布时，该模型称为高斯混合模型（Gaussian Mixture Model，GMM）［4-5］。当用于图像分割时，有限混合模型的一个缺点是该模型认为像素之间的关系是独立的，并没有考虑像素的空间关系。为克服有限混合模型的缺点，文献［6-7］随后提出了一些基于马尔科夫随机场的模型，虽然考虑了像素的空间邻域关系，但是标签概率比例（像素属于某些类的概率）不能在期望最大化（Expectation Maximization，EM）方法的M步骤中得到封闭解。

基于空间邻域关系的高斯混合模型（Gaussian

Mixture Model Based on Spatial Relationships，GMMS）［8］不仅考虑了像素间的关系，而且采用梯度下降法进行参数优化，减小了方法的复杂度。但是该方法只对高斯噪声有明显效果，然而，在工程应用中，噪声模型往往表现出非高斯性，即概率密度函数分布往往表现出较厚的尾部统计特性［9］，此时的噪声已不是高斯噪声，而是重尾噪声。而Student-t分布具有尖峰后尾的统计特性［10］，因此，本文将采用基于Student-t分布的混合模型验证其对含重尾噪声图像的处理效果。

2 基于有限混合模型的图像分割

2.1 有限混合模型

由于单个概率分布只有一个峰值，然而许多实际现象的分布都是由多个峰值组成。因此单个概率分布不能对现实中具有多个峰值的现象进行有效地模拟。有限混合模型供了一种用简单密度模拟复杂密度的有效方法。FMM是同一类型但不同参数的分布函数的线性叠加［11］。FMM的定义公式如下：

θ）可以是任意的概率分布函数。若 P（χθ）是高斯分布，则该FMM被称为高斯混合模型。注意πk需要满足0≤πk≤1和

2.2 基于空间邻域关系的高斯混合模型

基于空间邻域关系的高斯混合模型是在标准高斯混合模型的基础上考虑像素的空间邻域关系。

设χi表示图像的第i个像素点，i=1，2，…，N，图像分为K类，Ωj表示第j（j=1，2，…，K）类。第i个像素点χi的密度函数为：

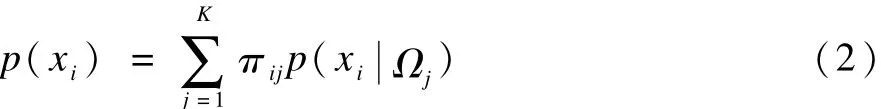
在GMMS中，πij考虑像素的空间邻域关系，每个像素点即使在同一类中也有不同的先验概率，其中，πij需要满足0≤πij≤1和每个高斯分布都是混合模型的一个部件，高斯分布为：其中，μj和σj分别为高斯分布的均值和协方差。根据式（2）得到对数似然函数：

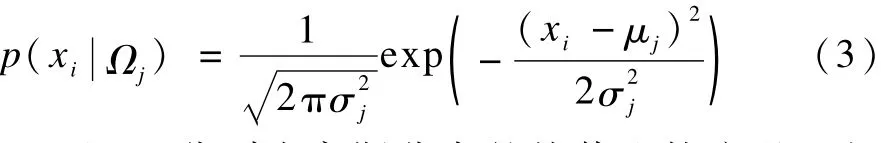
第i个像素点的后验概率为：

由于对数似然函数是非负递增函数，根据经验求解负对数似然函数较为方便：

最大化对数似然函数相当于最小化式（7），也就相当于最小化下式：

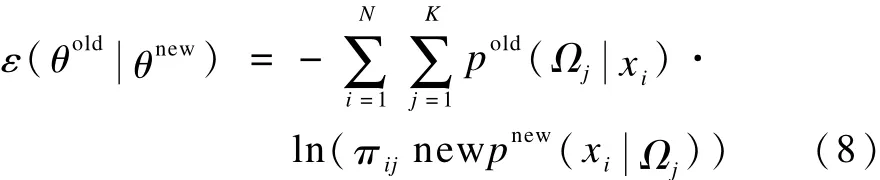
其中，ε是误差函数，因此，最大化似然函数 L相当于最小化 ε。将优化结果带入式（5），再利用式（6）进行像素标记。

2.3 Student-t分布

在概率论和统计学中，Student-t分布经常应用在对呈正态分布的总体的均值进行估计。它是对2个样本均值差异进行显著性测试的学生t测定的基础。t检定改进了Z检定，不论样本数量大或小皆可应用。在样本数量大（超过120等）时，可以应用Z检定，但Z检定用在小的样本会产生很大的误差，因此，样本很小的情况下得改用学生t检定。在数据有3组以上时，因为误差无法压低，此时可以用变异数分析代替学生t检定。

一元Student-t分布定义如下［12］：

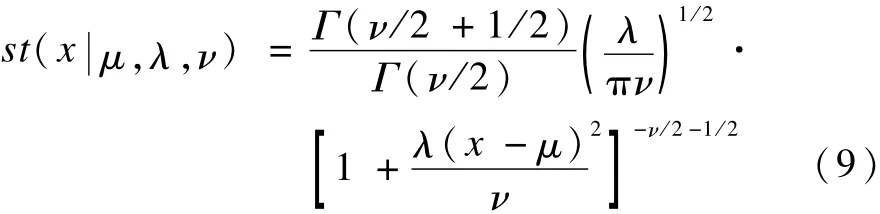
其中，μ和λ分别表示Student-t分布的均值和精度，λ的值等于方差的逆；Γ（·）表示伽马函数；ν为Student-t分布的自由度，用于调整Student-t分布的尾部长度，它对Student-t分布的影响如图1所示。

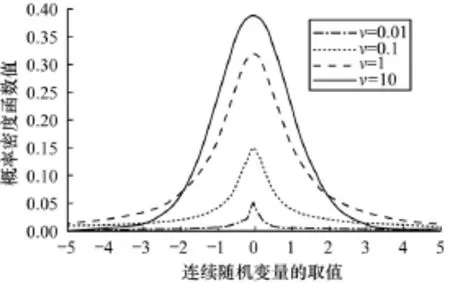
图1 不同ν的Student-t分布

当ν=1时，Student-t分布就成了柯西分布，当ν＞1时，μ就成为Student-t分布的均值，当ν趋于无穷大时，Student-t分布就以相同的均值μ和精度λ趋近于高斯分布。

2.4 重尾噪声模型

高斯噪声、椒盐噪声、乘性噪声、重尾噪声［13］等是常见的噪声模型，而本文研究含重尾噪声的图像分割，重尾噪声分布模型主要有Erlang噪声、Lap lace噪声、Cauchy噪声、负指数噪声以及混合高斯噪声等。其概率密度函数如下：

（1）Erlang分布：

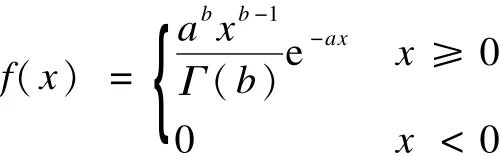
其中，a＞0，b是正整数，均值为b/a，协方差为b/a2。

（2）Laplace分布：

其中，均值为 μ；协方差为2σ2。

（3）Cauchy分布：

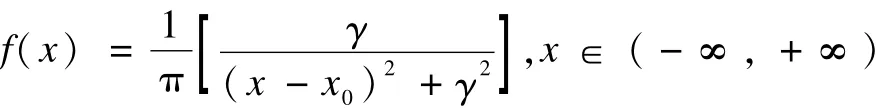
其中，χ0是位置参数；γ＞0是尺度参数；均值不存在。

（4）负指数分布：

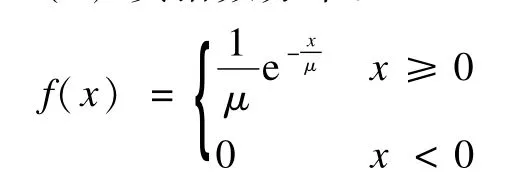
其中，均值为 μ；方差为 μ2。

（5）混合高斯噪声由高斯噪声获得，即：

其中：2

α为闪光频率，一般情况下，α很小，μ1=μ2且

3 Student-t分布处理重尾噪声方法

以一个基于标准高斯混合的新模型用于图像分割，其优点在于其先验概率 πij考虑像素的领域关系，和基于马氏随机域的模型相比，该方法需要更少的参数而且更容易实现。

3.1 基于空间邻域关系的先验概率

首先，给定一幅由U×V个像素点构成的灰度图。用 χ（u，ν）表示图像的第 i个像素点 χi，其中，i= U（u-1）+ν；u=1，2，…，U；ν=1，2，…，V。充分考虑像素间的关系，如图2所示。

图2 相邻像素点3×3像素窗口

第i个窗口χ（u，ν）邻域点的像素集定义为：

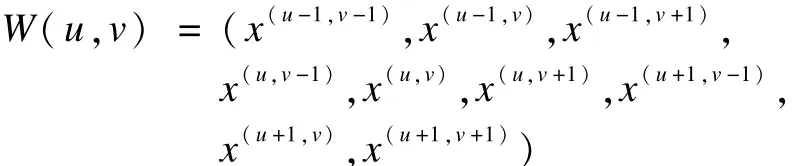
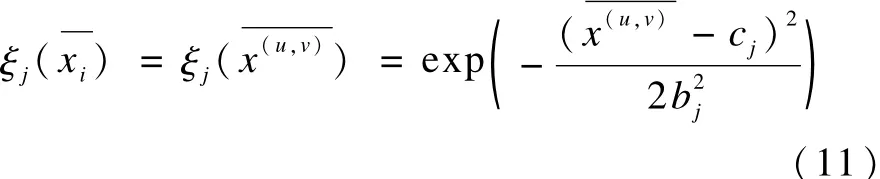
其中，cj和bj（j=1，2，…，k）是优化后的参数，优化方法将在后续内容中详细介绍。

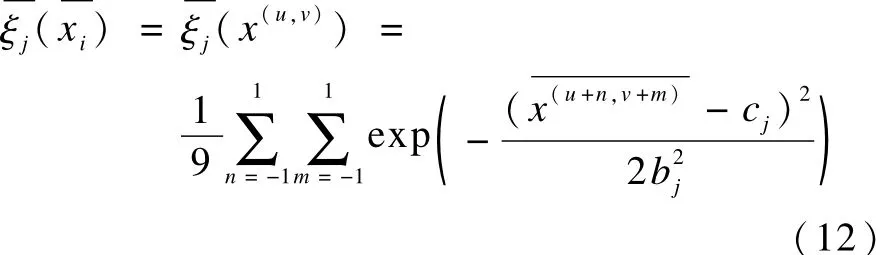
该方法将像素的空间邻域关系和其先验概率πij结合起来。因此：

先验概率之所以考虑空间约束是因为图像中相邻像素在某种意义上是相似的。基于这种关系，在图像中用像素领域的均值替换每个像素值。注意πij需要满足0≤πij≤1和它在图像分割中起到了过滤器的作用，可以将被噪声污染的图像变得平滑。将式（13）得到的先验分布结合式（4）得到对数似然函数：

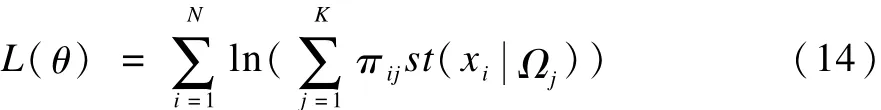
其误差函数为：

前文主要讨论像素χi属于Ωj的概率估计问题。为了计算后验概率需调整参数 Θ=（μj，λj，cj，bj），j=1，2，…，K，最小化误差函数。采用梯度下降法优化参数从而最小化误差函数。

3.2 参数优化方法

（1）用K-均值（K-means）初始化参数μj和σj，且得到Θold。

（2）根据式（5）得到其后验概率：

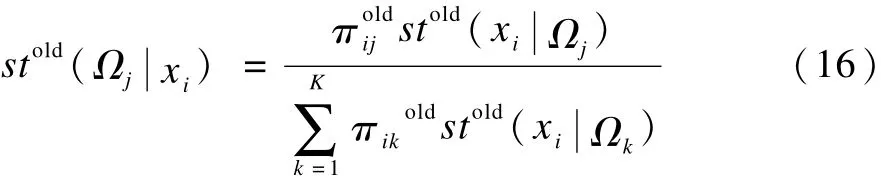
（3）更新参数Θ=（μj，λj，cj，bj），得到新的参数Θnew，通过梯度下降法［14］计算参数：

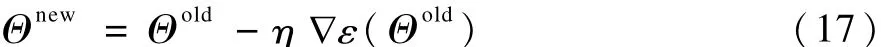
其中，▽ε=（∂ε/∂μj，∂ε/∂λj，∂ε/∂cj，∂ε/∂bj）；η是参数率，取η=10-7。下面给出ε对μj的偏导数为：

同理，ε对λj的偏导数为：

同理，ε对cj的偏导数为：

其中：

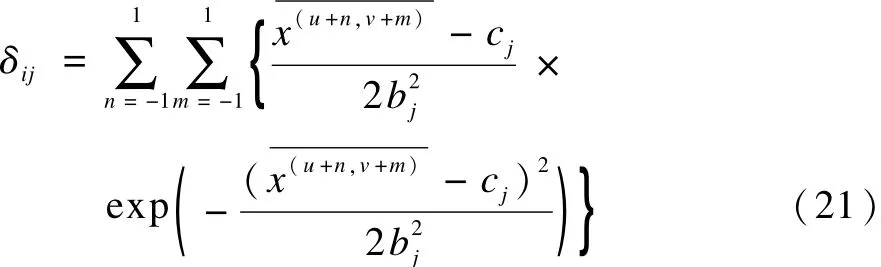
同理，ε对bj的偏导数为：

其中：

（4）如果负对数似然函数的值变化较大，或参数Θ变化较大，则令Θold=Θnew，同时返回步骤（2）。

4 实验结果及分析

其中，MMCR取值范围为［0，1］，其值越小图像分割结果越好。当MMCR的值为0时，表示错误分类的像素数目为0，即分割完全正确。当MMCR的值为1时，表示错误分类的像素数目与整个图像的像素数目相等，即分割完全错误。

4.2 图像合成实验对比

第1组实验使用的是由128×128像素构成的合成图像，它有4种灰度值［0.25，0.5，0.75，1］，图片分为4类。图3（a）为原始图像，图3（b）为被混合高斯噪声腐蚀的图像，其中，参数值alPhal=0.1，均值μ1= μ2=0.1，方差σ1=0.002，σ2=0.2，图3（c）～图3（e）分别为K-means，模糊C-均值（Fuzzy C-means，FCM）和GMMS的分割结果，其误分率分别达到9.95%，10.28%，22.81%，本文方法的分割结果如图3（f）所示，其误分率降到3.31%，低于其他方法。从表1可以看出，K-means，FCM，GMMS 3种方法在处理被重尾噪声腐蚀的图像时误分率很高，而本文方法的误分率相对较低。由于重尾噪声下图像有严重的拖尾情况，K-means，FCM，GMMS不能有效处理重尾噪声下图像的拖尾情况。然而，Student-t分布可以有效处理图像拖尾情况。因此，本文方法取得较好的分割效果。

4.1 评价指标

目前对图像分割的评价还没有一个统一的标准，图像分割结果的评价带有很大的主观性。为了客观、量化的评价图像分割结果，本文采用误分率（Misclassification Ratio，MCR）［15］进行分割结果评价。

MCR主要用于合成图像分割结果的量化评价。定义如下：

图3 第1组实验图像分割结果

表1 第1组实验图像的混合高斯噪声误分率对比 %

第2组实验是对添加Laplace噪声的图像进行处理，使用的图像由128×128像素构成，图像分为3类，其灰度值为［0，0.5，1］。图4（a）为原始图像，图4（b）为被Laplace腐蚀的图像，其中，均值μ=0.001，方差σ=0.06。图4（c）～图4（e）分别为K-means，FCM和GMMS的分割结果，其误分率分别达到0.81%，0.69%，0.37%，本文方法的分割结果如图4（f）所示，其误分率降到0.12%，低于其他方法。因为Student-t分布相对而言处理重尾噪声效果较好。第2组实验图像分割结果MCR对比如表2所示。

图4 第2组实验图像分割结果

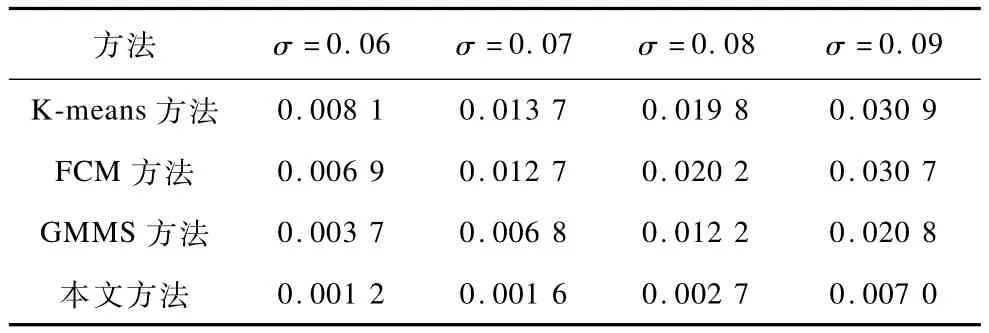
表2 第2组实验图像的Lap lace噪声误分率对比 %

第3组实验比较的是各方法对添加高斯混合噪声图像的处理效果，图像同样是人工合成的，由128×128像素构成，它有2种灰度值［0.47，0.07］，图片分为2类。图5（a）为原始图像，图5（b）为被混合高斯噪声腐蚀的图像，其中，参数值alPhal=0.25，均值 μ1=μ2=0.1，方差 σ1=0.002，σ2=0.2。图5（c）～图5（e）分别为K-means，FCM和GMMS的分割结果，其误分率分别达到50.27%，49.96%，4.66%，本文方法的分割结果如图5（f）所示，其误分率降到1.08%，低于其他方法。

图5 第3组实验图像分割结果

4.3 真实图像实验对比第4组实验使用的是由128×128像素构成的真实图像，图像分为4类，分别是白质、灰度、脑髓液和背景。图6（a）是真实分割结果，图6（b）为被混合高斯噪声腐蚀的图像，其中，alPhal=0.1，均值μ1= μ2=0.1，方差 σ1=0.002，σ2=0.2。图 6（c）～图6（e）分别为K-means，FCM和GMMS的分割结果，其误分率分别达到37.46%，59.16%，11.33%，本文方法的分割结果如图6（f）所示，其误分率降到9.78%，低于其他方法。

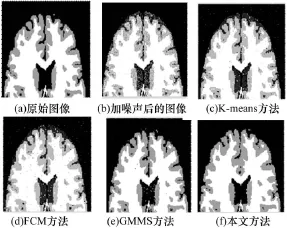
图6 第4组实验图像分割结果

第5组实验比较的是各方法对真实图像的处理效果，由 192×128像素构成，图像分为 2类。

图7（a）是真实分割结果，图7（b）为被混合高斯噪声腐蚀的图像，其中，alPhal=0.1，均值 μ1=μ2= 0.1，方差σ1=0.002，σ2=0.2。图7（c）～图7（e）分别为K-means，FCM和GMMS的分割结果，其误分率分别达到37.20%，36.09%，21.74%，本文方法的分割结果如图7（f）所示，其误分率降到18.62%，同样优于其他方法。

图7 第5组实验图像分割结果

第6组实验是对添加Laplace噪声的图像进行处理，使用的真实图像由100×100像素构成，图像分为4类，图8（a）为原始图像，图8（b）为被Lap lace腐蚀的图像，其中，均值 μ=0.001，方差 σ=0.06。图8（c）～图8（e）分别为K-means，FCM和GMMS的分割结果，其误分率分别达到20.58%，21.89%，32.66%，本文方法的分割结果如图8（f）所示，其误分率降到10.42%，低于其他方法。因为Student-t分布相对而言处理重尾噪声效果较好。

图8 第6组实验图像分割结果

实验结果表明，本文方法在处理被重尾噪声腐蚀的合成图像和真实图像时，其误分率较低，分割效果较好。这是由于重尾噪声尾部较长，而Student-t分布拥有相对于高斯分布较长的尾部，因此它成为高斯分布的健壮替代。这进一步的说明了该方法的有效性和可行性。

5 结束语

本文提出一种基于Student-t分布的混合模型用于图像分割，不仅考虑像素的空间邻域关系，而且使用梯度下降法进行参数估计。通过实验结论验证了基于Student-t分布的混合模型图像分割方法的优越性。然而，本文的参数 k是用户根据先验知识自己设定的，主观性影响较大，今后将针对该问题进行研究，进一步完善该方法。

［1］ Mclachan G，Peel D.Finite Mixture Model［M］. New York，USA：John Wiley&Sons，2000.

［2］ Bishop C M.Pattern Recognition and Machine Learning［M］.Berlin，Germany：Springer，2006.

［3］ Titterington D M，Smith A F，Makov U E.Statistical Analysis of Finite Mixture Distributions［M］.New York，USA：John Wiley&Sons，1985.

［4］ Jain A K，Duin R PW.Statistical Pattern Recognition：A Review［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（1）：4-37.

［5］ Redner R A，Walker H F.Mixture Densities，Maximum Likelihood and the EM Algorithm［J］.SIAM Review，1984，26（2）：195-239.

［6］ Choi H S，Haynor D R，Kim Y.Partial Volume Tissue Classification of Multichannel Magnetic Resonance Images——A Mixel Model［J］.IEEE Transactions on Medical Imaging，1991，10（3）：395-407.

［7］ Santago P，Gage H D.Quantification of MR Brain Im ages by Mixture Density and Partial Volume Modeling［J］.IEEE Transactions on Medical Imaging，1993，12（3）：566-574.

［8］ Thanh M N，Jonathan Q M.Gaussian-mixture-model-based Spatial Neighborhood Relationships for Pixel Labeling Problem［J］.IEEE Transactions on System s M an and Cybernetics Part B：Cybernetics，2012，42（1）：193-202.

［9］ Mukherjee A，Sengupta A.Estimating the Probability Density Function of a Nonstationary Non-Gaussian Noise［J］.IEEE Transactions on Industrial Electronics，2010，57（4）：1429-1435.

［10］ Wang Zhimin，Song Qing.Robust Curve Clustering Based on a Multivariate t-distribution Model［J］.IEEE Transactions on Neural Networks，2010，21（12）：1976-1984.

［11］ 熊太松，章 毅.基于统计混合模型的图像分割方法研究［D］.成都：电子科技大学，2013.

［12］ Bishop C M.Pattern Recognition and Machine Learning［M］.Berlin，Germ any：Springer，2006.

［13］ 王 桥.数字图像处理［M］.北京：科学出版社，2009.

［14］ Lange K，Fessler J A.Globally Convergent Algorithms for Maximum a Posteriori Transmission Tomography［J］.IEEE Transactions on Image Processing，1995，4（10）：1430-1438.

［15］ Zhang Y，Brady M，Smith S.Segmentation of Brain MR Images Through a Hidden Markov Random Field Model and the Expectation-maximization Algorithm［J］.IEEE Transactions on Medical Imaging，2001，20（1）：45-57.

编辑 刘 冰

Mixture Model Image Segmentation Method Based on Student-t Distribution

NIU Yirong，WANG Shitong

（School of Digital Media，Jiangnan University，Wuxi214122，China）

Traditional image segmentation methods can not effectively adapt to the case of image smearing with heavytailed noise.And the result of segmentation is not satisfactory in dealing with the image contaminated by heavy-tailed noise.This paper presents an image segmentation method based on Student-t distribution.The method calculates the prior probability according to the spatial relationship between the pixels，uses gradient descent method to optimize parameters so as to minimize the error function.The posterior probability values of pixels are obtained based on the optimal parameters. Image segmentation is realized by marking the pixels.Experimental results show that the misclassification ratio is lower and the performance is better when using the proposed method to deal with the image contaminated by heavy-tailed noise，compared with the traditional K-means and Fuzzy C-means（FCM），etc.

Student-t distribution；heavy-tailed noise；image segmentation；spatial neighborhood relationship；Gaussian Mixture Model（GMM）

牛艺蓉，王士同.基于Student-t分布的混合模型图像分割方法［J］.计算机工程，2015，41（10）：204-209.

英文引用格式：Niu Yirong，Wang Shitong.Mixture Model Image Segmentation Method Based on Student-t Distribution［J］.Computer Engineering，2015，41（10）：204-209.

1000-3428（2015）10-0204-06

A

TP391

牛艺蓉（1989-），女，硕士研究生，主研方向：人工智能，模式识别，数字图像处理；王士同，教授。

2014-10-28

2014-12-02E-mail：yirong1027@126.com