地球形成和演化过程中的分异能计算方法研究
耿煜, 王君恒,2,3*
1 中国地质大学(北京)地球物理与信息技术学院, 北京 100083 2 中国地质大学 地质过程与矿产资源国家重点实验室, 北京 100083 3 地下信息探测技术与仪器教育部重点实验室(中国地质大学,北京), 北京 100083
地球形成和演化过程中的分异能计算方法研究
耿煜1, 王君恒1,2,3*
1 中国地质大学(北京)地球物理与信息技术学院, 北京 100083 2 中国地质大学 地质过程与矿产资源国家重点实验室, 北京 100083 3 地下信息探测技术与仪器教育部重点实验室(中国地质大学,北京), 北京 100083
地球形成初期,构成地球的物质在组成上是大致均一的.目前地球的地核-地幔-地壳圈层结构,是由分异作用形成的.分异过程释放的能量称为分异能.Sorokhtin和Chilingarian等人从行星吸积的定义出发,导出了基于地球内部密度分布的势能计算公式,计算出的分异能大小为1.698×1031J.本文采用计算球体势能的思路,导出分异能计算的解析公式和数值计算公式,通过求取原始地球模型与均匀分层模型、PREM模型的势能差计算分异能.两种方法的计算结果分别为1.535×1031J和1.698×1031J.前者与Sorokhtin等的结果相近,后者与之相同.本文初步分析了方法间的异同以及造成结果偏差的主要原因.
重力分异; 势能; 分异能; 吸积能; PREM
1 引言
为说明地球的成因,国内外已有四十多种假说(王君恒等, 2010, 2012, 2013),其中较为普遍认同的有我国天文学家戴文赛首次提出的新星云假说(戴文赛和胡中为, 1980).该假说认为:地球的形成与太阳系形成密不可分,要经过“原始星云→星云盘→尘层→星子→行星”共5个阶段(戴文赛和胡中为, 1979).
吸积是形成行星地球的最终阶段.关于吸积有两种不同的观点,即均一吸积说和非均一吸积说(朱志祥, 1982).通常认为,均一吸积说可能性较大,即原始地球是一个接近均质的球体,并没有明显的分层现象(戴文赛和陈道汉, 1976).根据对地球外核成分的认识不同,均一吸积说又可分为金属化核说和铁核说(Schmidt, 1957).冲击波实验表明(朱志祥, 1980):外核物质的密度比铁在外核条件下的密度小15%左右.所以外核物质除了铁外,还应有少量的轻元素.较可能的轻元素是硫和氧.
但是,与原始地球不同,目前的地球内部分为地壳、上下地幔和内外地核等几个大的圈层.这种圈层结构是由分异作用形成的(腾吉文, 2003).在地球自身引力和内部温度的共同作用下,流动的轻物质上涌形成外层,流动的重物质下降形成内层,故构成了地球圈层物质的分异过程(Rubie et al., 2007).在圈层分异、调整过程中,地球内部能量的产生、迁移、转化和消耗,是制约整体作用过程的决定要素.因此,分异能的计算是一个关键性问题.
Sorokhtin等(2010)从行星吸积的定义出发,导出了基于地球内部密度分布的势能计算公式,计算出的分异能大小为1.698×1031J.Flasar和Birch (1973)计算了目前地球和原始地球两种不同情形下地球吸积过程中重力所做的功,两者的差1.66×1031J即为地球分异过程中损失的势能.另有不同学者的估算(Lyubimov,1968; Vityazev,1973; Keondjian and Monin,1977)表明,地球分异过程中释放的重力势能在1.46×1031J到2×1031J之间.
本文采用计算球体势能的思路,通过求取原始地球和目前地球的势能差计算分异能.首先在均匀分层模型下推导出地球势能的解析表达式,计算所得分异能大小为1.535×1031J,与Sorokhtin等的结果相近.该方法能够以解析形式表达出地球的势能,可以避免数值求和的繁琐步骤,较前人方法相比计算更加简洁.本文进一步在分层更加精细的PREM全球参考模型下,应用地球势能的数值计算公式,得出的分异能大小为1.698×1031J,在所给精度范围内与Sorokhtin等结果一致.该公式使用压强表示地球的势能,降低了由模型间差异所带来的误差,较前人方法具有更高的准确性.本文初步分析了方法间的异同以及造成结果偏差的主要原因.
2 前人计算所用吸积做功法
Sorokhtin等(2010)认为:在数值上,地球的吸积能Ea等于其重力势能的相反数(根据定义势能总是负的).任何系统的势能取决于该系统的构造格局,在此处讨论的情形中则是地球内部的密度分布,表达式为
(1)
(2)
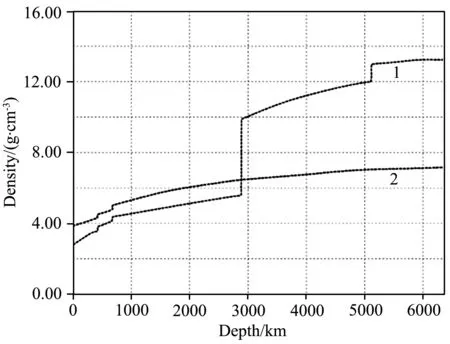
图1 普遍接受的地球内部密度分布(1为目前地球,2为原始地球)Fig.1 Accepted density distribution within Earth(1 is present-day Earth;2 is primordial Earth)
其中U为地球的势能;m(r)是半径为r的球体内部所包含的地球质量;ρ(r)为地球在半径r处的物质密度;γ=6.673×10-11m3·kg-1·s-2为引力常数;R=6.371×106m为地球的平均半径.目前和原始地球内部密度分布见图1(Naimark and Sorokhtin, 1977a,b).
为了确定原始地球的吸积能,明确其内部密度分布是必需的.该分布是建立在地球物质的平均组分(表1)及硅酸盐和金属冲击压缩数据(Naimark and Sorokhtin, 1977a,b)之上的.高压下基于冲击压缩数据的造岩氧化物密度测定的目前技术具有2%~4%的精度(Sorokhtin et al., 2010).用这种方法测定出的原始地球内部密度分布见图1(Naimark and Sorokhtin, 1977a,b).
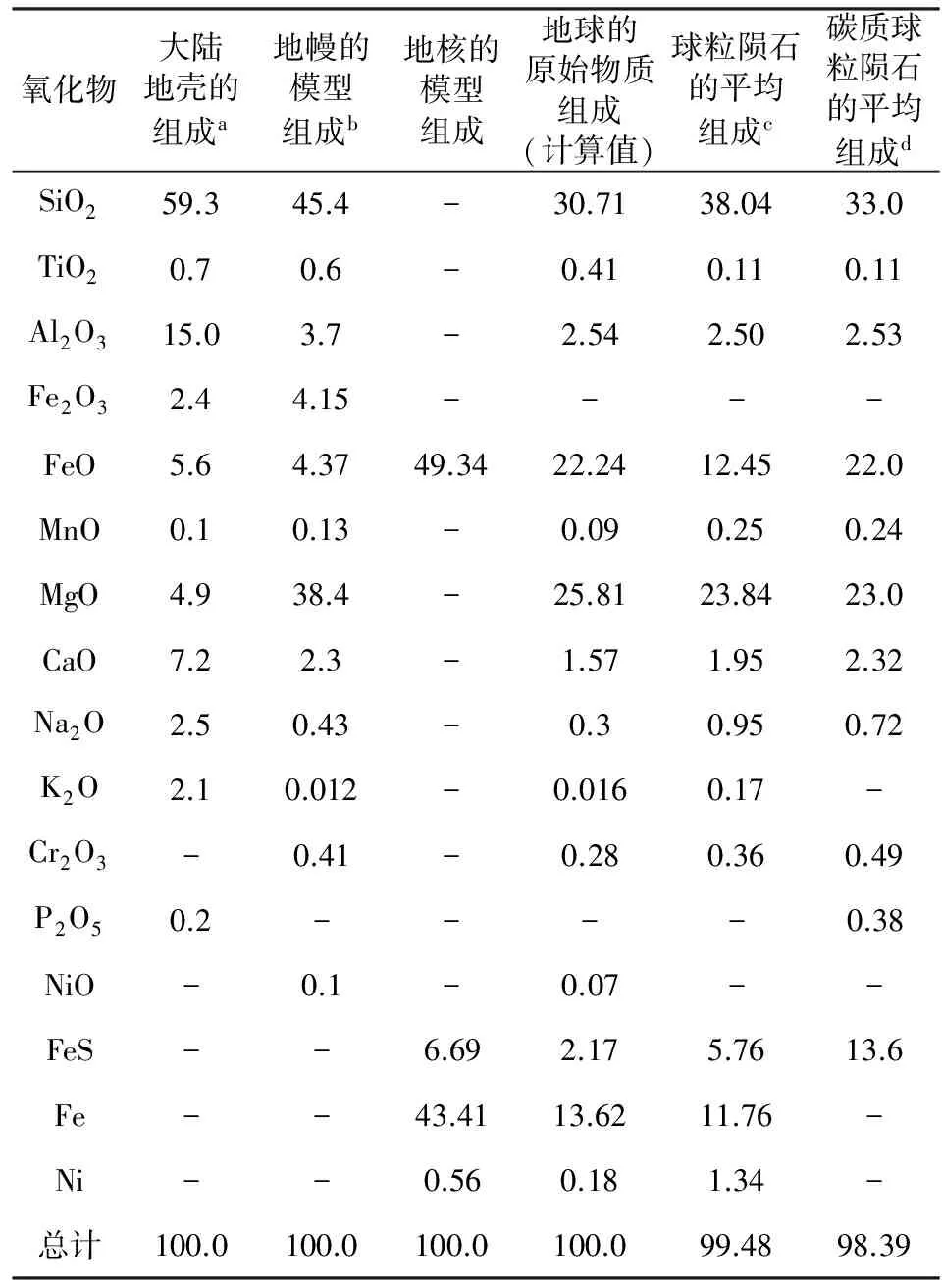
表1 目前地球和原始地球的物质组成(Sorokhtin et al., 2010)Table 1 Composition of present-day Earth and primordial Earth matter (Sorokhtin et al., 2010)
地球质量:M=5.9772×1027g;地核质量:Mcore=1.9404×1027g;内核质量:Mcore1=0.1083×1027g;过渡带质量:Mcore2=0.1299×1027g;外核质量:Mcore3=1.8321×1027g;地幔质量:Mm=4.0143×1027g;大陆地壳质量:Mcc=2.25×1025=0.0225×1027g.aRonov and Yaroshevsky, 1978;bRingwood, 1966; Dmitriyev, 1973;cUrey and Craig, 1953;dBarsukov, 1981.
使用式(1)及(2)来计算46亿年前地球形成过程中释放的吸积能.该能量(约等于其初始势能)是巨大的:U(4.6)≈ -23.255×1031J.在数值上,重力分异能等于分异过程刚好开始(即约40亿年前)之前均匀地球的势能与目前分层地球的势能差为(Sorokhtin et al., 2010)
Eg=U4.0-U0.0,
(3)
目前地球的势能为-24.952×1031J(Sorokhtinetal., 2010).因此根据定义,重力分异的总能量为[-23.255-(-24.952)]×1031J=1.698×1031J.
除该方法外,Flasar和Birch(1973)计算了目前地球和原始地球两种不同模型下地球形成过程中重力所做的功.分别基于Dziewonski和Gilbert(1972)的目前地球模型与Birch(1965)的原始地球模型,他们得出目前地球的吸积能为2.490×1032J,原始地球的吸积能为2.324×1032J.根据分异能的定义,两者的差1.66×1031J即为地球分异过程中损失的势能.
此外,Monteux等(2009)一起研究了行星分异的相关数值模型,给出了分异过程中的势能损失计算公式为
(4)
其中Ω为行星的体积.虽然作者没有给出具体的推导思路和地球分异能的计算结果,但是其推导可能应用了与Flasar和Birch (1973)相同的思路.
3 均匀分层模型下的解析积分法
本文尝试在均匀分层地球模型下通过球坐标积分推导出原始地球和目前地球的势能表达式,分别计算原始地球和目前地球的势能.再根据分异能的定义,用原始地球的势能减去目前地球的势能,得出分异能的大小.
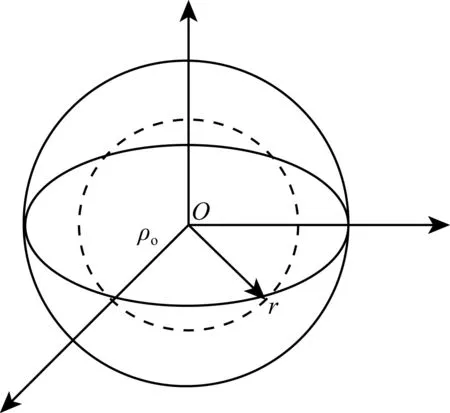
图2 密度均匀的原始地球模型Fig.2 A primordial Earth model which consists of a homogeneous mixture of the materials of the present core and mantle
作为近似,将原始地球看作密度均匀的标准球体,并以球心为原点建立球坐标系(图2).设无限远处的势能U∞=0,原始、均匀地球的密度为ρ0,原始地球的半径为R0,以原点为球心选取一个半径为r、厚度为dr的薄球壳(0 dm=ρ0×4πr2dr, (5) 势能为 dU4.0=-r×g(r)dm=-4πr3ρ0g(r)dr. (6) 从0到R0积分,得原始地球的总势能为(Solomon, 1979) (7) 其中 (8) 式(8)是半径为r处的重力加速度(Monteux et al., 2009).代入地球势能的表达式,得: (9) 图3 以地核的平均密度和地壳加地幔的平均密度代替实际密度分布的目前地球模型Fig.3 A present-day earth model in which its density distribution is substituted by the mean density of core and the mean density of crust and mantle 为了给出目前地球势能的解析表达式,设理想的目前地球及其地核均为标准球体,并将地壳并入地幔之中.以地核的平均密度代替地核的实际密度分布,以地壳加地幔的平均密度代替地壳和地幔的实际密度分布.这样,本文提出的目前地球模型内部是一个匀质的地核,外部则是地幔与地壳合在一起的壳幔层,构成“地核-壳幔层”的双层结构. 以球心为原点建立球坐标系(图3),设地核的平均密度为ρc,地核的平均半径为Rc.类比原始地球势能的推导方法,并参考式(7)的形式,写出地核势能的积分表达式为 (10) 其中 (11) 式(11)是半径为r处的重力加速度(0 (12) 对于地壳和地幔,依旧参考式(7)的形式,写出其势能表达式为(Rc (13) 此时,r处的重力加速度由两部分质量提供:一是地核质量,二是所取薄球壳包围的地壳和地幔质量,即: (14) 代入整理得 (15) 将地核与地壳和地幔的势能相加,便得到目前地球的势能表达式为 U0.0=Uc+Um. (16) 假设原始地球和目前地球表面重力加速度相同,原始地球和目前地球的平均密度相同.计算所需数据(Anderson, 1989;JeffreysandSinger, 2009)如下:地球表面重力加速度g0=9.8156 m·s-2;原始、均匀地球的密度ρ0=5.514×103kg·m-3;原始地球的半径R0=6.355×106m;目前地球的半径R=6.371×106m;地核的平均密度ρc=10.76×103kg·m-3;地核的平均半径Rc=3.485×106m;地壳加地幔的平均密度ρm=4.400×103kg·m-3.计算所得原始地球的势能为U4.0≈ -22.131×1031J,目前地球的势能为U0.0≈ -23.665×1031J.于是根据定义,分异能为Eg=U4.0-U0.0≈[(-22.131)-(-23.665)]×1031J=1.535×1031J. 作为对地核-壳幔层双层结构的改进,可以在内核—外核—下地幔—上地幔—地壳的五层结构下推导并计算目前地球的势能.但是,在模型被进一步细化之后,以解析形式给出的地球势能表达式非常复杂,从而给均匀分层解析法的推导和计算带来不便.因此,本文仅给出在地核-壳幔层模型下目前地球势能的推导与计算过程. 总结前人的计算公式(1)、(2)、(3)及(4)发现,他们均采用地球内部密度分布表示出地球的吸积能.经比较,不同的地球模型(Bolt, 1957; Bullen, 1965; Dziewonski et al., 1975; Martinec et al., 1986)在压强分布上的差异要低于密度分布上的差异,特别是在地心附近.根据计算,在深度为6371 km处,Bullen地球密度模型(Bullen, 1938)所给出的压强数值相对于PREM模型(Dziewonski and Anderson, 1981)偏小约3.53%,密度偏小约7.02%.可见,若能以压强表示出地球的势能,则能够降低因模型间差异而带来的误差. 对于一个密度仅为半径函数的处于流体静力平衡状态下的球体,势能可以表达为多种不同的形式(王君恒等, 2010, 2012, 2013): φdmr (17) 其中 (18) (19) 总质量为M,球体的半径为R,压强为P,密度为ρ.当压强P为关于r的已知函数时,最后一种形式对于势能的计算是较为方便的.并且从不同密度模型中压强的差异较小这一事实可以推知:若使用地球内部半径和压强分布计算目前地球的势能,在不同密度模型下计算出的势能差异不会过大.对于原始地球的势能,本文将采用Birch的原始地球模型(表2)进行计算;对于目前地球的势能,本文将采用Dziewonski和Anderson的初步地球参考模型(表3)进行计算. 将式(17)改写为求和形式为 (20) 其中i为由内向外逐层所做的编号,N为所用模型的数据长度,即可用程序逐步完成该计算.在编写了程序后,本文计算出原始地球的势能为U4.0≈ -23.338×1031J(详见表4),目前地球的势能为U0.0≈ -25.036×1031J(详见表5).于是按照定义,分异能Eg=U4.0-U0.0≈ [(-23.338)-(-25.036)]×1031J=1.698×1031J. 在本文所选取的原始和地球模型下,PREM数值求和法得出了与Sorokhtin等相同的结果.由于选用压强可以减低不同模型间差异带来的误差,当不同模型间密度分布差异较大时,该方法比Sorokhtin等的方法具有更高的准确性. 表2 Birch原始地球模型下半径、密度和压强分布(Birch,1965)Table 2 Radius,density and pressure distribution under Birch primordial earth model (Birch,1965) 表3 PREM模型下半径、密度和压强分布(Dziewonski and Anderson,1981)Table 3 Radius,density and pressure distribution under preliminary reference earth model (Dziewonski and Anderson,1981) 续表3 表4 Birch原始地球模型下势能的计算步骤Table 4 Calculation procedures of potential energy under Birch primordial earth model 续表4 表5 PREM模型下势能的计算步骤Table 5 Calculation procedures of potential energy under preliminary reference earth model 续表5 (1) 不同于前人的吸积做功法,均匀分层解析法能够以解析形式表达出原始地球和目前地球的势能,计算过程简洁,避免了数值求和的繁琐步骤. (2) 在实际情况下,地核、地幔和地壳的密度随半径增大而逐渐减小.这使得均匀分层模型下计算出的目前地球势能比实际情况偏大,该偏差进一步导致了分异能的计算结果偏小. (3) 由于分层更多的地球模型会给均匀分层解析法的推导和计算带来困难,本文只给出地核-壳幔层双层结构下目前地球势能的推导与计算过程. (4) 考虑到不同的地球模型在压强分布上的差异小于密度分布上的差异,PREM数值求和法采用了压强表达地球的势能,可降低由模型间差异所带来的误差. (5) 在本文所选取的原始和目前地球模型下,PREM数值求和法得出了与Sorokhtin等的方法相同的结果.并且当不同模型间密度分布差异较大时,该方法比Sorokhtin等的方法具有更高的准确性. (6) 目前地球的分异活动仍没有停止,只是分异不再是形成核-幔-壳结构的全面大规模活动.在此过程中,一部分分异能被地球的弹性压缩所消耗,绝大部分分异能转化为地球内部的热量. (7) 后续研究中深入探讨的主要内容有:地球演化过程中的其他物理机制(如放射性元素的衰变等)能够为地球提供的热能,理论上这些热能总共能使地球升高的温度;分异能的释放速率与释放总量随时间的变化规律等重要问题. Anderson D L. 1989. Theory of the Earth. Boston, MA: Blackwell Scientific Publications, 366.Barsukov V L. 1981. Outlines of Comparative Planetology. Moscow: Izd-vo Nauka, 184-185. Birch F. 1965. Energetics of core formation.JournalofGeophysicalResearch, 70(24): 6217-6221.Bolt B A. 1957. Earth models with continuous density distribution.GeophysicalJournalInternational, 7(6): 360-368. Bullen K E. 1938. Note on the density and pressure inside the Earth.TransactionsandProceedingsoftheRoyalSocietyofNewZealand, 67: 122-124. Bullen K E. 1965. Models for the density and elasticity of the Earth′s lower core.GeophysicalJournalInternational, 9(2-3): 233-252. Dai W S, Chen D H. 1976. Critical review of theories on the origin of the solar system.ActaAstronomicaSinica(in Chinese), 17(1): 93-105. Dai W S, Hu Z W. 1979. On the origin of the asteroids.ActaAstronomicaSinica(in Chinese), 20(1): 33-42. Dai W S, Hu Z W. 1980. On the origin of the solar system.ScienceChina(in Chinese), (3): 254-266. Dmitriyev L V. 1973. Mid-Oceanic ridge bedrock geochemistry and petrology[Ph. D. thesis]. Moscow: Moscow University, 45. Dziewonski A M, Gilbert F. 1972. Observations of normal modes from 84 recordings of the Alaskan earthquake of 1964 March 28.GeophysicalJournalInternational, 27(4): 393-446. Dziewonski A M, Hales A L, Lapwood E R. 1975. Parametrically simple Earth models consistent with geophysical data.PhysicsoftheEarthandPlanetaryInteriors, 10(1): 12-48. Dziewonski A M, Anderson D L. 1981. Preliminary reference Earth model.PhysicsoftheEarthandPlanetaryInteriors, 25(4): 297-356. Flasar F M, Birch F. 1973. Energetics of core formation: A correction.J.Geophys.Res., 78(26): 6101-6103. Jeffreys H, Singer S F. 2009. The Earth: Its origin, history and physical constitution.PhysicsToday, 12(9): 61-62. Keondjian V P, Monin A S. 1977. Calculations on the evolution of the planetary interiors.Tectonophysics, 41(1-3): 227-242. Lyubimov E A. 1968. Thermal Properties of the Earth and the Moon. Moscow: Nauka. Monteux J, Ricard Y, Coltice N, et al. 2009. A model of metal-silicate separation on growing planets.EarthandPlanetaryScienceLetters, 287(3-4): 353-362. Naimark L M, Sorokhtin O G. 1977a. Energy of Earth′s Gravity Differentiation.TectonicsofLithosphericPlates, 42-56. Naimark L M, Sorokhtin O G. 1977b. The density distribution in the Earth′s model with the herzolite mantle composition and iron oxide core.TectonicsofLithosphericPlates, 28-41. Ringwood A E. 1966. The chemical composition and origin of the Earth.AdvancesinEarthScience, 276-356. Ronov A B, Yaroshevsky A A. 1978. Chemical Composition of the Earth′s Crust and of her Shells. Moscow: Tectonosphere of Earth, Nedra, 376-402. Rubie D C, Nimmo F, Melosh H J. 2007. Formation of Earth′s core. ∥Schubert G ed. Treatise on Geophysics. Oxford: Elsevier, 51-90. Schmidt O Y. 1957. Four Lectures on the Theory of the Origin of the Earth. Izd-vo AN SSSR. Solomon S C. 1979. Formation, history and energetics of cores in the terrestrial planets.PhysicsoftheEarthandPlanetaryInteriors, 19(2): 168-182. Sorokhtin O G, Chilingarian G V, Sorokhtin N O. 2010. Evolution of Earth and Its Climate: Birth, Life and Death of Earth. St. Louis, MO: Elsevier, 160-164. Teng J W. 2003. Introduction to Solid Geophysics (in Chinese). Beijing: Earthquake Press, 80-91. Urey H C, Craig H. 1953. The composition of the stone meteorites and the origin of the meteorites.GeochimicaetCosmochimicaActa, 4(1-2): 36-82. Vityazev A V. 1973. On the energy of gravitational differentiation in the Earth.Izv.Akad.NaukSSSR,Ser.Fiz.Zemli, (10): 86-88. Wang J H, Guo L, Wang J N, et al. 2010. The change of Earth oblateness in its history.ProgressinGeophysics(in Chinese), 25(1): 143-150, doi: 10.3969/j.issn.1004-2903.2010.01.021. Wang J H, Li X J, Zhang Y Y, et al. 2013. The lower limit of variation of the Earth′s oblateness in geological epoch.ChineseJ.Geophys. (in Chinese), 56(3): 842-847, doi: 10.6038cjg20130313.Wang J H, Zhang Y Y, Xin Z X, et al. 2012. Upper limit variation of the Earth′s Oblateness in geological epoch and impact analysis on the Dai Wensai′s Nebular Hypothesis.Geoscience(in Chinese), 26(6): 1168-1174. Zhu Z X. 1980. Several hypotheses about the mantle and core formation.ChineseJournalofNature(in Chinese), 3(11): 852-855, 810. Zhu Z X. 1982. Some problems on the origin of the Earth.ActaGeophysicaSinica(in Chinese), 25(2): 172-180. 附中文参考文献 戴文赛, 陈道汉. 1976. 太阳系起源各种学说的评价. 天文学报, 17(1): 93-105. 戴文赛, 胡中为. 1979. 论小行星的起源. 天文学报, 20(1): 33-42. 戴文赛, 胡中为. 1980. 论太阳系的起源. 中国科学, (3): 254-266. 腾吉文. 2003. 固体地球物理学概论. 北京: 地震出版社, 80-91. 王君恒, 郭雷, 王健楠等. 2010. 地球扁率在其历史上的变化. 地球物理学进展, 25(1): 143-150, doi: 10.3969/j.issn.1004-2903.2010.01.021. 王君恒, 李新均, 张煜颖等. 2013. 地球扁率在地质历史上的变化下限. 地球物理学报, 56(3): 842-847, doi: 10.6038cjg20130313. 王君恒, 张煜颖, 辛志翔等. 2012. 新星云假说下地球扁率变化上限及影响因素. 现代地质, 26(6): 1168-1174. 朱志祥. 1980. 关于地幔和地核形成的几种假说. 自然杂志, 3(11): 852-855, 810. 朱志祥. 1982. 关于地球起源的几个问题. 地球物理学报, 25(2): 172-180. (本文编辑 张正峰) Research on calculation methods of differentiation energy during the formation and evolution of the earth GENG Yu1, WANG Jun-Heng1,2,3* 1SchoolofGeophysicsandInformationTechnology,ChinaUniversityofGeosciences,Beijing100083,China2ChinaUniversityofGeosciences,StateKeyLaboratoryofGeologicalProcessesandMineralResources,Beijing100083,China3KeyLaboratoryofGeo-detection(ChinaUniversityofGeosciences,Beijing),MinistryofEducation,Beijing100083,China According to Dai Wensai′s nebular hypothesis, the formation of the Earth was closely related to the formation of the solar system, which can be described as “primordial nebular-protoplanetary disc-konisphere-planetesimal-planet”. Accretion was the last stage during the formation of the Earth. Generally considered, homogeneous accretion has a greater possibility, which means that the primordial Earth was a nearly homogeneous body without significant stratification. However, different from the primordial Earth, the present-day Earth is divided into crust, upper mantle, lower mantle, outer core and inner core. This layering structure was formed by the differentiation process. During the differentiation and adjustment of the layers, the generation, migration, conversion and consumption of the Earth′s internal energy was the decisive factor that restricted the whole process. Therefore, the calculation of differentiation energy is a pivotal issue.Starting from the definition of planet accretion, Sorokhtin et al. derived a potential calculation formula which is based on the density distribution within the Earth, and the calculated differentiation energy is 1.698×1031J. Flasar and Birch calculated the work done by gravity in the process of the Earth′s accretion in the light of primordial Earth and present-day Earth. The difference between these two quantity, 1.66×1031J is the potential energy loss in the process of the Earth′s differentiation. Estimates given by other authors suggest that the gravitational potential energy released during the process of the Earth′s differentiation is between 1.46×1031J and 2×1031J.The idea of calculating the potential energy of a sphere was adopted in this paper, and differentiation energy was calculated by evaluating the potential energy difference between primordial Earth and present-day Earth. Firstly, the analytic formula of the Earth′s potential energy was derived based on a uniformly layered Earth model. The calculated differentiation energy is 1.535×1031J which is close to the result given by Sorokhtin et al. Further, using a more sophisticated model, the preliminary reference Earth model (PREM), and by applying the numerical formula of the Earth′s potential energy, the differentiation energy was calculated to be 1.698×1031J, which is the same as the result of Sorokhtin et al. within the given precision.Different from the “accretion work method” in previous studies, the“uniform layered analytic method” gives the analytic formula for the potential energy of primordial Earth and present-day Earth, from which the tedious steps of numerical summation were avoided. In the actual case, the density of core, mantle and crust decreases with radius increasing. This will make the potential energy of present-day Earth under uniform layered Earth model larger than that in the actual case, which can further make the calculated differentiation energy small. Since an Earth model with more layers can bring inconvenience to the derivation and calculation of the “uniform layered analytic method”, only the derivation and calculation on the “core-mantle two-layer structure” was given in this paper.Considering that the difference of pressure is smaller than the difference of density between different Earth models, the “PREM numerical summation method” uses pressure instead of density to describe the Earth′s potential energy, which can reduce the error brought by the differences between models. Using the Earth models adopted in this paper, the “PREM numerical summation method” gives the same result as the method of Sorokhtin et al. Moreover, when density distributions given by different Earth models vary significantly, this method can lead to more reliable results than the method of Sorokhtin et al.At present, the Earth′s differentiation has not yet stopped, but it is no longer comprehensive and large-scale activity which forms the core-mantle-crust structure. In this process, a portion of the differentiation energy was consumed by the Earth′s elastic compression, while most of it was converted into the Earth′s internal heat. Subsequent research should focus on the heat sources provided by other physical processes during the evolution of the Earth and other relevant issues, such as the decay of radioactive elements, the total temperature the Earth raised by absorbing this heat, and the releasing rate and releasing amount of differentiation energy with time. Gravitational differentiation; Potential energy; Differentiation energy; Accretion energy; PREM 10.6038/cjg20151009. Geng Y, Wang J H. 2015. Research on calculation methods of differentiation energy during the formation and evolution of the earth.ChineseJ.Geophys. (in Chinese),58(10):3530-3539,doi:10.6038/cjg20151009. 耿煜, 男, 1989年生, 天津人, 中国地质大学(北京)地球物理与信息技术学院,硕士,目前在美国孟菲斯大学地震研究中心,主要从事天然地震研究. E-mail: ygeng1@memphis.edu *通讯作者 王君恒, 男, 1962年生, 山东青岛人, 博士, 中国地质大学(北京)地球物理与信息技术学院副教授, 主要从事应用地球物理和理论地球物理研究. E-mail: w1128@cugb.edu.cn 10.6038/cjg20151009 P311 2015-01-06,2015-10-08收修定稿 耿煜,王君恒. 2015. 地球形成和演化过程中的分异能计算方法研究.地球物理学报,58(10):3530-3539,
4 PREM模型下的数值求和法




5 结论
——《势能》

