基于神经网络和证据理论的DCT电控系统故障诊断

孔慧芳， 段 锐， 鲍 伟

（合肥工业大学 电气与自动化工程学院，安徽 合肥 230009）

0 引 言

双离合器自动变速器是近年来国内外汽车企业和研究者关注的一种新型自动变速器，具有传动效率高、安装空间紧凑、换挡过程无动力中断等特点。在车辆实际运行过程中，由于恶劣环境影响或者驾驶员操作不当等原因，自动变速器电控系统中的各零部件难免会发生故障，这将直接影响整车的安全性能和使用性能。因此，能否准确、快速地对自动变速器电控系统故障做出诊断至关重要。

目前，一些自动变速器智能故障诊断技术得到了一定的发展与应用。文献［1］采用基于模糊神经网络的故障自诊断方法，实现了对自动变速器电控系统故障的模糊诊断；文献［2］设计了基于支持向量机的多值分类器，对自动变速器故障进行识别和诊断，取得了良好的效果；文献［3］从自动变速器的故障现象入手，借助模糊理论归纳故障现象与故障原因的对应关系，以便准确锁定故障部位，提高了诊断精度。

然而由于自动变速器电控系统故障的多征兆性、不确定性以及获取到的故障数据的不完整性，单一的智能诊断方法在使用中会存在诊断精度不高的情况。而数据融合技术具有能充分利用各个数据源之间包含的冗余和互补信息的优点，可以提高系统决策的准确性和鲁棒性，为故障诊断确诊率的提高提供了一条有效途径［4］。

因此，本文应用D－S证据理论数据融合技术，将BP神经网络和RBF神经网络2种故障诊断方法的诊断结果进行决策融合，提高了DCT电控系统故障诊断的诊断精度。

1 DCT电控系统原理及故障分析

1.1 DCT电控系统原理

DCT电控系统由变速器控制单元（transmission control unit，TCU）、输入轴转速传感器、加速踏板位置传感器等传感器、比例电磁阀、开关电磁阀等执行器件组成，如图1所示。TCU通过采集加速踏板位置、车速、发动机转速、离合器油压等信号，经过计算、分析，获知汽车的当前运行状态，并根据一定的换挡规律判断出换挡时刻，然后向电磁阀、电机等执行器件输出控制信号，从而使离合器、选换挡机构等执行相应的动作，实现自动变速的综合控制。

图1 DCT电控系统结构

1.2 DCT电控系统故障分析

经大量查阅资料并综合故障诊断专家经验，得到以下几种DCT电控系统常见故障：输入轴转速传感器故障、输入1轴转速传感器故障、输入2轴转速传感器故障、输出轴转速传感器故障、车速传感器故障、发动机转速传感器故障、加速踏板位置传感器故障、挡位传感器故障、油温传感器故障、离合器油压传感器故障、主油压阀故障、离合器压力控制阀故障、选挡电磁阀故障、多路开关阀故障、传感器供电故障。

由于DCT故障征兆的特征参数和故障类别之间存在非线性映射关系，因此，可以利用神经网络的非线性映射逼近能力，根据特征参数的变化得出故障诊断模型，以便正确识别出相应的故障原因。本文以DCT无法由1挡升2挡为例，对产生这一故障征兆的不同故障类别进行分类。

2 故障诊断系统

本文建立的基于神经网络和D－S证据理论的故障诊断系统结构如图2所示。该系统由BP神经网络诊断系统、RBF神经网络诊断系统和基于D－S证据理论的决策融合系统3个子系统组成。

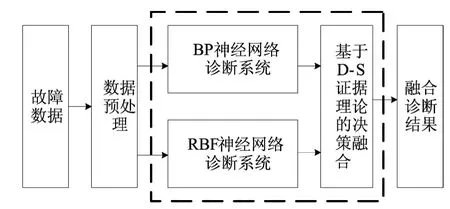
图2 基于神经网络和D－S证据理论的故障诊断系统结构

2.1 BP神经网络诊断子系统

BP神经网络是一种全局逼近的多层前馈型网络。根据Kolmogorov定理［5］，一个3层的前向网络具有对任意精度连续函数的逼近能力，故将采用3层BP神经网络进行DCT电控系统故障诊断。

在对DCT无法由1挡升2挡故障征兆的特点进行详细分析之后，选取加速踏板位置传感器电压、车速、发动机转速、输入1轴转速、输入2轴转速、离合器1油压和离合器2油压这7个特征参数作为网络的输入。选取故障分类结果作为网络的输出，包括正常、加速踏板位置传感器故障、车速传感器故障、发动机转速传感器故障。隐含层神经元的个数可通过经验公式得到，即

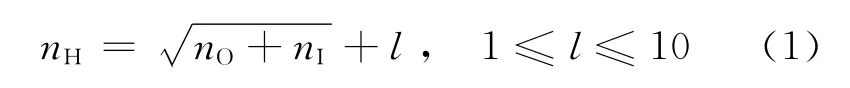
其中，nI为输入层神经元数目；nO为输出层神经元数目；nH为隐含层神经元数目；l为1～10之间的整数。

2.2 RBF神经网络诊断子系统

径向基函数（RBF）神经网络是一种局部逼近的3层前向网络。其隐含层节点的激活函数采用的是径向基函数。选择高斯函数作为径向基函数，隐含层节点的输出为：

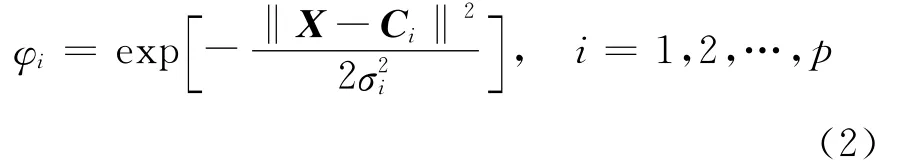
其中，φi第i个隐含层节点的输出；σi为第i个隐含层节点的高斯函数半径，其大小决定了网络的复杂程度；X为网络的输入向量；Ci为第i个隐含层节点高斯函数的中心向量；p为隐含层节点数。

RBF神经网络的隐含层到输出层的映射为线性映射［6］，即

其中，yk为第k个输出层节点的输出；wki为隐含层到输出层的加权；θk为隐含层阈值；q为输出层节点数。

RBF神经网络的输入和输出与BP神经网络相同，此处不再赘述。

2.3 基于D－S证据理论的决策融合子系统

在故障诊断中，D－S证据理论的识别框架Θ为诊断对象可能发生的故障类别。定义基本概率分配为识别框架Θ上的一个2Θ→［0，1］的函数m，并且满足：

其中，∅为空集；A为Θ中任一命题。

决策融合的关键是将BP神经网络和RBF神经网络作为证据理论的2个独立证据，通过将两者的输出值进行转换，确定每个证据下各种故障类别的基本概率分配。采用（4）式构建基本概率分配m：

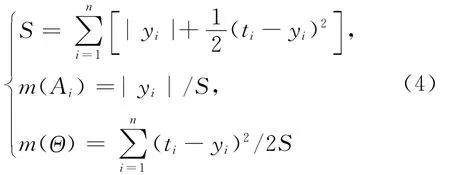
其中，n为故障类别个数；yi为神经网络第i个输出层节点的实际值；ti为神经网络第i个输出层节点的期望值；Ai为第i种故障类别；m（Θ）为证据的不确定度。

根据（4）式得到的基本概率分配来计算单个证 据 下 故 障 类 别Ai的 信 度 区 间 （Bel（Ai），pl（Ai）），计算公式如下：

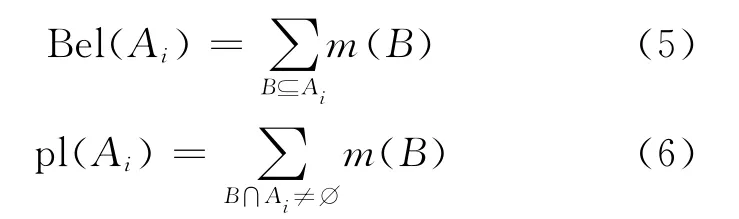
利用证据合成公式［7］计算2个证据融合后各故障类别的信度区间（Bel，pl）和证据的不确定度m（Θ），根据以下规则［7－8］确定最终诊断结果Aa。

规则1 Bel（Aa）＝ max｛Bel（Ai）｝。

i

规则2 Bel（Aa）－Bel（Ai）＞ε1，Bel（Aa）－m（Θ）＞ε2。

规则3m（Θ）＜ε3。

其中，ε1、ε2、ε3为预先设定的阈值。

3 故障诊断仿真实例

为了验证基于神经网络和D－S证据理论的故障诊断方法的有效性，本文以DCT无法由1挡升2挡为例，人为设置故障类别为加速踏板位置传感器故障（A1）、车速传感器故障（A2）及发动机转速传感器故障（A3），与正常状态（A0）共同构成了决策融合的识别框架Θ＝ ｛A0，A1，A2，A3｝。共记录试验时4种故障类别下的特征参数103组，其中99组作为训练样本，剩余4组作为测试样本，利用Matlab进行神经网络的训练和诊断测试［9］。

BP神经网络输入层和输出层的神经元数目分别为7和4。根据（1）式，并经过多次仿真后，确定隐含层的神经元数目为10。其中，训练函数选择trainlm，隐含层和输出层神经元传递函数均选择logsig，最大训练次数为3 000，学习率为0.01，目标均方误差为0.001。经仿真，训练次数为35时，达到规定的期望误差。RBF神经网络输入层和输出层的神经元数目同样分别为7和4，目标均方误差为0.001，高斯函数的扩展速度为1，经过仿真后，确定隐含层的神经元数目为6。经仿真，训练次数达到6时，达到规定的期望误差。分别选取每种故障类别下的1组特征参数作为测试样本来测试训练好的故障诊断系统，诊断结果见表1～表3所列。

根据仿真结果确定阈值ε1＝0.6，ε2＝0.7，ε3＝0.05。通过比较分析表1～表3可以发现，在表1中，对于第3组诊断结果，A0的信度区间为（0.177 408，0.204 307），A2的 信 度 区 间 为（0.748 636，0.775 535），两者不满足诊断规则2，无法分辨出故障类别；另外，对于第2组诊断结果，其证据的不确定度为0.027 288，相对其他组来说不确定度较高。

在表2中可以看出，RBF神经网络可以很好地诊断4种故障类别，但是对于第1组诊断结果，同样存在证据的不确定度较高的问题。

在表3中，对于BP和RBF 2种神经网络单独诊断时，信度区间均高的故障类别的信度相对上升，信度区间均低的故障类别的信度相对降低。例如第3组诊断结果中，A2的信度区间由（0.748 636，0.775 535）、（0.953 372，0.954 190）提高到（0.996 740，0.996 770）。A0的信度区间由（0.177 408，0.204 307）、（0.001 248，0.002 066）降低为（0.000 539，0.000 569），因此诊断故障类别为A2。

同时各组诊断结果的不确定度明显减小，最大的不确定度为0.000 305。

综上可知，由于基于神经网络和D－S证据理论的故障诊断系统充分利用了不同证据的冗余和互补信息，该系统能够显著提高故障诊断的诊断精度。

表1 BP神经网络诊断结果

表2 RBF神经网络诊断结果

表3 决策融合结果

4 结束语

本文将神经网络和D－S证据理论相结合，利用BP神经网络和RBF神经网络的输出来构造D－S证据理论中的基本概率分配，使得基本概率分配不再完全依赖专家的主观赋值。然后将2种神经网络的诊断结果用D－S证据理论合成规则进行决策融合，得出最终诊断结果。同时，以DCT无法由1挡升2挡为例，通过仿真验证了该故障诊断方法的有效性和准确性。

［1］ 孔慧芳，何吉柱.模糊神经网络在自动变速器电控系统故障自诊断中的应用［J］.合肥工业大学学报：自然科学版，2010，33（4）：501－505，518.

［2］ 杜灿谊，杨翠丽，潘 威.支持向量机在汽车自动变速器故障识别中的应用［J］.汽车工程，2012，34（3）：241－244.

［3］ 卫绍元，王冬梅，张忠洋.基于模糊理论的汽车自动变速器故障诊断系统［J］.机械设计与制造，2011（1）：230－232.

［4］ Zhou Ruixiang，Lin Tingqi，Ban Jiandong，et al.Fault diagnosis of airplane hydraulic pump［C］／／Proceeding of the 4th World Congress on Intelligent Control and Automation，Beijing，2002：3150－3152.

［5］ 李少远，王景成.智能控制［M］.北京：机械工业出版社，2005：100－102.

［6］ 李国勇.神经模糊控制理论及应用［M］.北京：电子工业出版社，2009：29－32.

［7］ 姜万录，李冲祥.神经网络和证据理论融合的故障诊断方法研究［J］.中国机械工程，2004，15（9）：760－764.

［8］ 杨 广，吴晓平.神经网络与D－S证据理论分层融合的柴油机综合故障诊断方法研究［J］.武汉理工大学学报：自然科学版，2011，35（3）：558－561.

［9］ 葛哲学，孙志强.神经网络理论与 MATLAB R2007实现［M］.北京：电子工业出版社，2007：46－69.