铝制圆环热变形受形体结构约束的原子仿真与实验研究
倪 洋, 苗恩铭, 张 辉, 陈瑞祥, 张雪峰
(1.合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230009;2.中国石油新疆油田分公司 工程技术研究院,新疆 克拉玛依834000)
精密机械设备工作过程中,由于受到温度影响,零件会产生热变形,使实际参数和几何形体偏离设计的最佳理想状态,产生热变形误差[1],最终影响整个系统或装备的性能、降低设备精度和使用寿命。
目前,国际上对于机械结构的设计,其考虑的热误差是基于热变形不受形体结构影响的状态,如不同形体结构零件热变形后仍然保持原有形状。本文对热变形误差补偿与修正技术进行了深入研究。根据形体各个尺寸热变形的相关性及非线性特点,提出了表面热变形具有微观非相似性[2],如平面和圆柱面,受热产生热变形后,表面发生变化,呈现为非平面和非圆柱面。这突破了传统热变形理论的约束,为高精度精密热变形误差的研究提供了一定的理论依据和思路。
形体结构对热变形影响已经被实验证实[3-6]。欧洲同步辐射光源ESRF研究发现,光学棱镜由于不同位置的厚度、形状,其在X光照射下产生的热变形不同,提出通过对反射镜形体结构进行优化,可以减小热变形[3]。但这些文献主要从宏观实验结果分析解释机械形体热变形现象,缺乏从原子角度微观机理进行的科学论证。
本文以圆环、方形环为研究对象,以分子静力学为理论基础,将结合修正莫斯势能的分子静力学模拟引入到对机械形体热变形受形体参数影响的理论探究中,从微观物体热变形机理和宏观实验2个方面对热变形受形体结构约束的现象和机理进行分析,为后期机械热结构设计提供新的研究思路,拓展形体热变形理论研究的方法。
近年来,分子静力学通过修正原子间势能函数的方式克服了传统分子静力学只能适用于绝对零度环境的劣势,现已广泛应用于研究材料从弹性到塑性变形的过程,以及裂纹萌生、位错形成等物理现象[7-9]。鉴于分子静力学的优点,本文以分子静力学为基础,对机械形体热变形进行研究。
1 将莫斯势能拓展至非绝对零度环境
传统分子静力学理论仅能采用绝对零度下的莫斯势能函数,本文将莫斯势能参数与实验已知的材料热膨胀系数之间建立关系,获得莫斯势能与温度之间的直接关系,从而把分子静力学应用拓展至任意温度下[10]。
莫斯势能函数为:
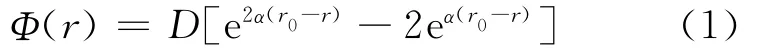
其中,D为势阱深度;α为势能参数;r0为两原子间的平衡距离。
当原子间距离r=r0时原子间达到平衡态,势能最小Φ(r)min=-D。为便于区分,把D写成D0,表示绝对零度时的势阱深度;r0表示绝对零度时原子间的平衡距离,r表示原子间的实际距离。对 于 铝 制 材 料[11]有:α=0.116 5nm,D0=0.270 3eV,r0=0.325 3nm。当r=r0,有能量最小值Φ(r0)=-D0。
修正后的莫斯势能形式为:

其中,DT为T温度下莫斯势能势阱深度;rT为T温度下原子间的平衡距离。
对(2)式求导可得原子间作用力公式为:

修正前后的势能曲线如图1所示,虚线为修正前T=0K的势能曲线,实线为修正后T>0的势能曲线。

图1 修正前后的Morse势能曲线
根据文献[10]提供的思路,得到铝的 Morse势能参数,见表1所列,从而确定出适用于非绝对零度环境的修正后莫斯势能函数参数。

表1 Morse势能函数在不同温度下的参数
由表1可以看出,随着温度升高,微观结构上表现为原子间平衡距离rT增大,宏观上表现为材料的热膨胀,对于本文中的铝圆环材料,则表现为圆环内外径的尺寸变化。
2 分子静力学仿真结果与分析
铝是面心立方晶格结构(face centered cubic,FCC),其晶格常数a=0.405nm。本文仿真建立了3组不同尺寸的圆环晶体模型。建立内径r1=8a,外径r2=16a的圆环模型的方法如下:
(1)建立16a×16a×1a的长方体,并得到每个原子的坐标。
(2)将那些与坐标原点(即圆环中心)之间的距离d小于8a和大于16a的原子删除。
(3)将剩下的原子坐标信息输入分子可视化软件(VMD)中显示,即可得到圆环模型,如图2所示。
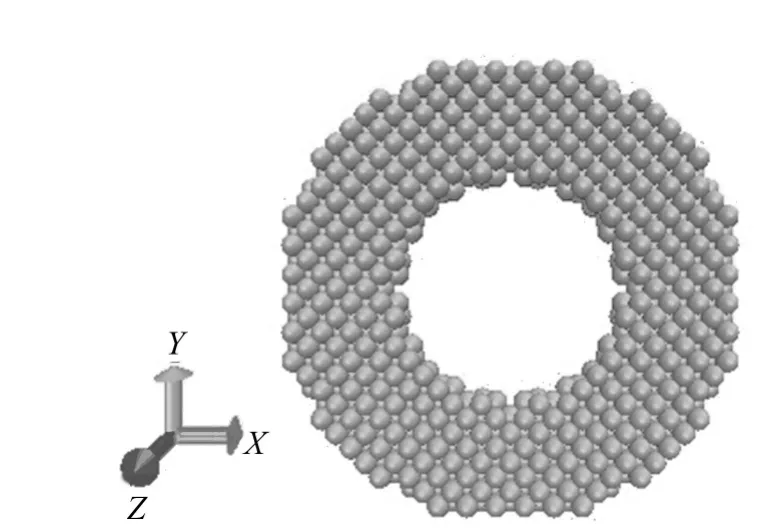
图2 铝圆环晶体模型
同理,对内径为8a,外径分别为12a、14a、16a、18a的圆环进行建模。编程仿真实现机械形体升温过程时,选取截断距离为rcut=0.5nm,边界为自由边界,弛豫时收敛精度ξ=5×10-5,温度T从0K升高至400K。
内外圆尺寸升温过程的分子静力学仿真结果见表2所列。表2结果表明,随着温度的上升,圆环内径尺寸减小。当圆环内径尺寸都为8a时,即内径尺寸一定,外径尺寸越大,内径尺寸减小越明显。随着温度的升高,圆环外径尺寸减小。当圆环内径尺寸都为8a时,外径尺寸越大,外径尺寸减小越明显。
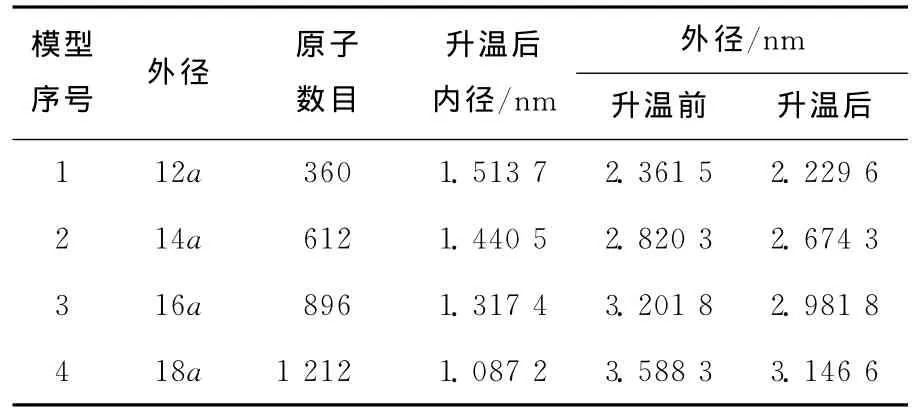
表2 不同外径下圆环分子静力学仿真结果
根据内外径变化数据,计算内外径的平均热膨胀系数,结果如图3所示。
由图3可看出,内径尺寸一定时,随着外径尺寸的增加,内径的平均热膨胀系数逐渐减小;外径的平均热膨胀系数先增大后减小。

图3 圆环升温后不同尺寸热膨胀系数变化曲线
3 宏观铝制圆环热变形实验
3.1 圆环内外径热变形测量实验方案
取3个内径均为30mm、外径分别为50、70、90mm的铝制圆环为实验对象,分别记为1#、2#、3#,3个圆环属于同一批次,加工处理方式完全相同。传感器支架安装在自主研发的基于“三三一原则”[13]的三坐标测量机上,该测量机采用了小阿贝误差三维测量系统[14],确保2个高温传感器探针布置于圆环径向上,同理,测内径热变形时将传感器置于内径方向。试验温度范围为-10~70℃,每隔10℃测1次。每个温度下保持1h,确保充分热膨胀。
实验采用ESPEC公司生产型号为ZL-04AGT的恒温箱,其温控范围为-40~+150℃,测温精度为±0.2℃,控温精度为±0.5℃;热变形数据采集系统由德国 Mahr Federal高精度电感传感器与Mahr Millitron832数显放大器组成,校正精度为±1数位,分辨率为0.1μm,线性误差小于0.025%FS。传感器放置于恒温箱内,读数时恒温箱处于密闭状态。
3.2 实验结果与分析
3个圆环内外圆在半径方向上相对于-10℃的热变形量见表3所列。由表3可以看出,内径热变形量受外径尺寸的影响,外径尺寸越大,内径热变形越小。根据计算得出3个圆环的内外径平均热膨胀系数如图4所示。
结果表明,对于环形机械形体,内径尺寸一定时,外径越大,内径的平均热膨胀系数越小;外径热膨胀系数处于铝材料的正常范围(18×10-6~23×10-6),而内径热膨胀系数受形体约束较大, 平均热膨胀系数偏小。
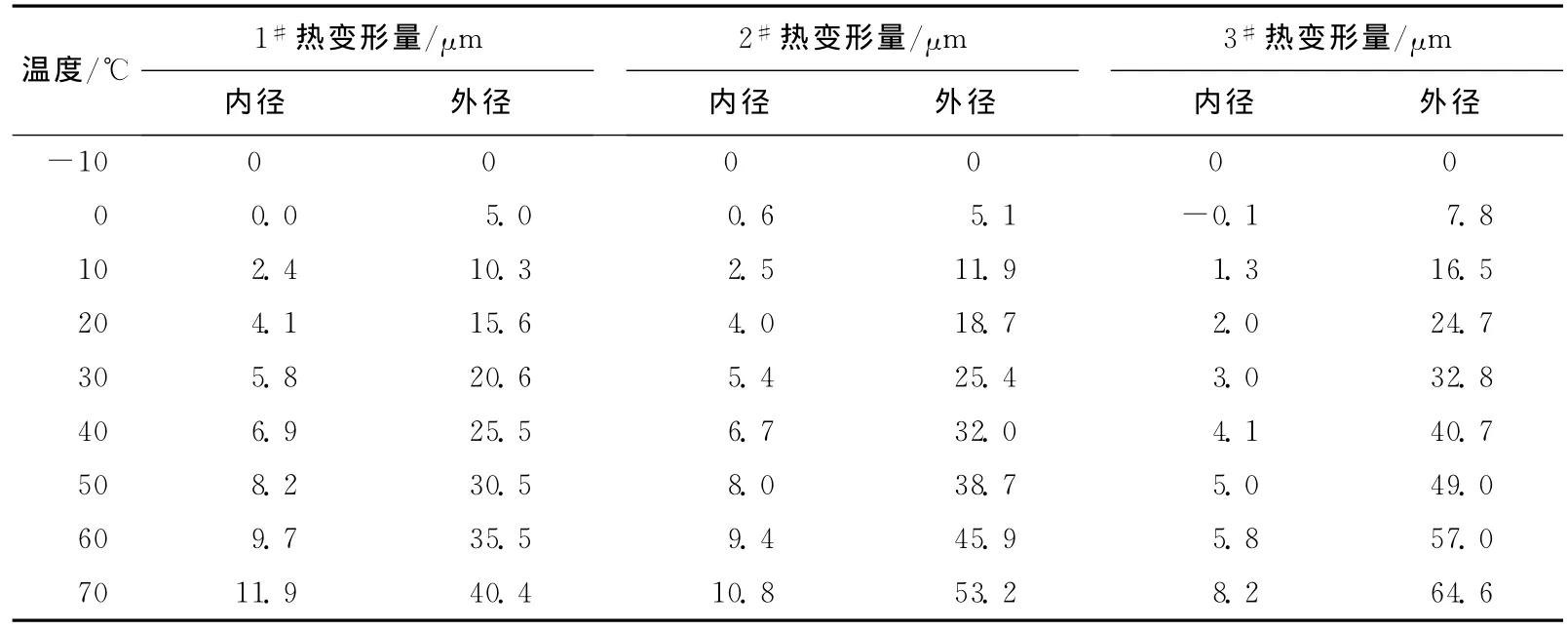
表3 不同圆环的热变形

图4 圆环内外径平均热膨胀系数
4 宏观铝制方形环热变形实验
取内径为30mm,外部尺寸为60mm的方形环,放置在三坐标测量机的平台上。试验温度范围为-10~70℃,每隔10℃测量1次,,每个温度下保持1h,确保充分热膨胀。
实验测量3次,测量角度分别为0°、22.5°、45°,测点示意图如图5所示。

图5 实际测点位置示意图
A、B、C点半径方向上相对于-10℃的热变形量见表4所列。根据结构对称性,将测点扩展到16个,拟合出方形环内径的变化曲线,如图6所示。计算得出方形环A、B、C 3点的内径平均热膨胀系数分别为13.8×10-6、10.7×10-6、8.8×10-6。

表4 方形环内半径热变形量 μm
由图6可以看出,方形环的内径热变形受形体结构的影响,在0°位置的热变形量要明显大于其他位置。


图6 不同温度时内径轮廓曲线
5 结 论
(1)本文将分子静力学理论与算法引入到机械形体热变形的研究中,拓展了热变形基础理论研究的思路和方法,具有一定的学术参考价值。
(2)微观上,根据纳米铝晶体圆环内外径尺寸的变化,分析受热膨胀规律,结果表明:纳米铝圆环的内外径之差,随着温度升高而变大,这与宏观材料热膨胀相一致;升温后,原子运动加剧,原子向内部空间移动,导致内径尺寸变小,外径尺寸减小。
(3)宏观铝圆环热变形测量实验结果显示:随着温度的升高,圆环的内外径尺寸均增大;内径相同的圆环,外径的平均热膨胀系数随着外径尺寸的增大而减小,内径的平均热膨胀系数也随着外径的增大而减小;外径热膨胀系数是内径热膨胀系数的2倍以上,说明内径受形体参数的约束和影响比外径要大。实验结果和理论规律相一致。宏观铝制方形环的热变形测量实验也表明了形体结构参数对热变形具有约束作用。
在现有的机械结构设计中,一般较少考虑到机械结构对形体热变形的影响。本文从微观和宏观角度论述了此现象。研究环形材料的热变形是研究机械零件最佳热配合结构的重要组成部分,对于控制热变形误差,提高机械工作状态下的配合精度具有非常重要的工程应用价值。
[1] 费业泰,苗恩铭,李桂华,等.机械热变形理论及应用[M].北京:国防工业出版社,2009:35-74.
[2] 费业泰,李光珂,徐婷婷,等.精密技术中零件非相似性热变形理论及应用研究[C]//第五届海峡两岸制造技术研讨会论文集,2006:227-230.
[3] Zhang L,Barrett R,Friedrich K,et al.Thermal distortion minimization by geometry optimization for water-cooled white beam mirror or multilayer optics[J].Journal of Physics:Conference Series,2013,425(5):052029.
[4] 苗恩铭,费业泰.形状参数对零件热膨胀影响研究[J].应用科学学报,2003,21(2):217-220.
[5] 罗 哉,费业泰.形状因素对精密技术中零件热变形的影响[J].机械工程学报,2009,45(1):235-238.
[6] Ramesh R,Mannan M A,Poo A N.Error compensation in machine tools:a review,PartⅡ:thermal errors[J].International Journal of Machine Tools and Manufacture,2000,40(9):1257-1284.
[7] Vinogradov O.A static analog of molecular dynamics method for crystals[J].International Journal of Computational Methods,2006,3(2):153-161.
[8] Vinogradov O.Using modified potential to account for nonzero temperature in molecular statics for crystals[J].Computational Materials Science,2008,41(4):493-497.
[9] Vinogradov O.A pseudo-atom method in potential energy minimization for crystals[J].Computational Materials Science,2008,44(2):547-551.
[10] Li G,Vinogradov O,Gubanov A.A modified Morse potential accounting for non-zero temperature in molecular statics for nickel crystals[J].Computational Materials Science,2012,62:126-130.
[11] Girifalco L A,Weizer V G.Application of the Morse potential function to cubic metals [J].Physical Review,1959,114(3):687-690.
[12] Touloukian Y S.Thermal expansion:metallic elements and alloys[M].New York:IFI/Plenum Data Company,1975:225.
[13] 费业泰,王晨晨,尚 平.微纳米级三维测量“331”系统及其测量方法:中国,CN101419044[P].2009-04-29.
[14] 苗恩铭,郭裕聪,刘善林,等.小阿贝误差三维测量系统:中国,CN202216672U[P].2012-05-09.
——《势能》

