模糊自整定PID航向控制算法优化及其性能评判

梅 强， 李丽娜， 陈国权，2， 蒋 娇， 马 峰

（1.集美大学 航海学院，福建 厦门 361021；2.大连海事大学 航海学院，辽宁 大连 116026）

模糊自整定PID航向控制算法3个参数Kp、Ki、Kd初始值的合理取值直接影响控制器的性能［1］，控制参数实际的船舶操纵过程应随船舶自身的工作状态（如载荷、吃水深度、航速等）及航行环境（如航线、水深、风浪流等）的不同而有很大的变化［2］。然而前期集成于船舶智能操控（Ship Intelligent Handling and Control，SIHC）仿真研究平台模糊自整定PID航向控制的算法，不能根据船舶操纵性及环境因素自动确定其初始值，而是直接引用DMI船模自带的PID自动舵提供的初始值，使得模糊自整定PID航向控制算法在风浪较大环境中对部分船模的控制效果不理想。

本文着重设计随船模及环境因素自动确定3个参数Kp、Ki、Kd的初始值算法，提高船舶的航向控制效果；同时对航向控制算法性能评判方法进行改进，提高算法评判的合理性。

1 PID航向控制器初始值自动确定算法

在传统的PID型自动舵设计时，采用的船舶航向控制系统模型一般都为标称模型［3］，即

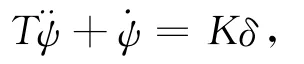
其中，K、T为船舶操纵性指数，K为船舶旋回性指数，T为船舶追随性指数；为船舶转首角加速度；为船舶转首角速度；δ为舵角。在自动控制理论中，由二阶的设计方法可以给出，即

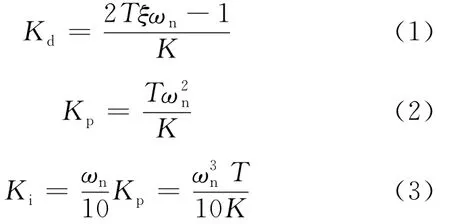
其中，ξ为系统的相对阻尼系数，为使系统有良好的性能，通常取0.8≤ξ≤1.0，对于严格阻尼的船舶，ξ取值为1.0；ωn为船舶的自然振荡频率，ωn＜ωδ，ωδ为舵机系统的自然频率。

在船舶航行中，优先考虑的问题有保持航向和节省能耗2个方面。在船舶操纵过程中，频繁操舵能保持航向的准确性，但同时会导致舵机能耗和船舶速度损失增大。考虑在不同情况下平衡这两者的关系，可选取二次型性能指标函数［4］，即

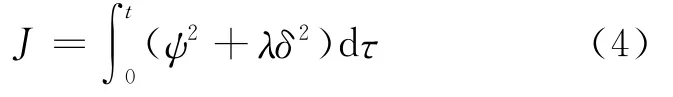
其中，λ为加权系数，一般取值在0.1～10之间；J为综合评判指标。

最优控制是使（4）式的二次型性能指标函数的取值为最小。根据线性二次型非零给定点输出调节器理论，最终可得最优控制率为：

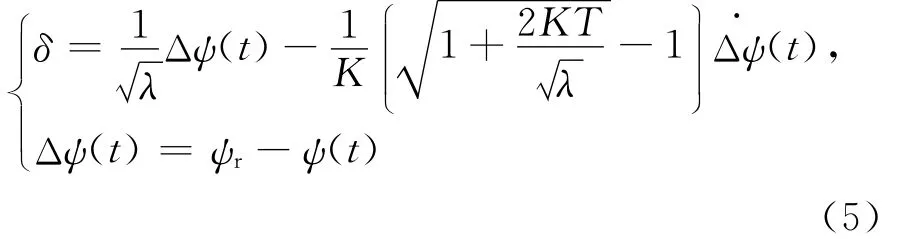
其中，ψr为设定航向；ψ（t）为实时航向。则有：

对于闭环控制系统，判断其是否具有稳定性的因素是原来的开环控制系统是否稳定。该闭环控制系统中的参数K、T和λ都大于0，因此其极点都位于s的左半平面，即该闭环控制系统是渐进稳定的。该系统是二阶振荡系统，自然振荡频率为［5］：

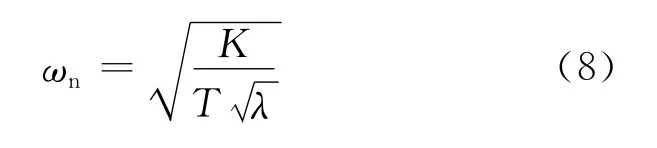
阻尼比为：

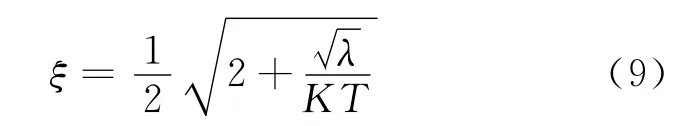
将（8）式分别代入（2）式和（1）式中，可得Kp、Kd的计算公式与（6）式和（7）式一致，由此，可将（8）式代入（3）式得Ki初始值计算公式为：

其中，λ的取值可根据环境情况灵活选取。

2 航向控制算法性能评判方法

2.1 航向跟踪性能评价

本文对文献［3］提出的基于模糊隶属函数的加权平均法进行了改进，提出一种航向跟踪性能的加权综合评判算法。该评判算法的数学表达式为：

其中，J为评判结果；ai为第i个指标的权重，一般要求∑ai＝1；xi为第i个指标值。

为了排除船舶自身船型、吨位等因素对评判结果的影响，本算法将评判算法指标中航向跟踪响应速度修改为航向跟踪延迟时间Δt，即在航向控制算法作用下由初始航向首次转到设定航向的时间，与船模以初始服务速度由初始航向满舵旋回到设定航向的时间之差。

由文献［4］的航向跟踪性能指标权值表改进的新权值表见表1所列。

表1 改进的航向跟踪性能指标权值

本文提出的加权综合评判方法即利用权值将航向跟踪过程中的超调量、振荡次数、操舵次数、跟踪延迟速度、最大舵值5个指标组织起来，形成一个包含各个侧面的综合指标［6］。采用均值化方法对各指标值做无量纲化处理，即

该评判算法中，评判结果是能耗、航向偏差、耗时等因素的综合值，由上述介绍可知，评判值越大，表明航向跟踪性能越差。

2.2 航向保持性能评价

相比于航向跟踪，航向保持阶段的转舵幅度小，航向偏差范围也较小，因此航向保持主要从航向偏差和舵机能耗2个方面考虑。航向保持性能评判算法是一种加权平均法，性能评判指标即为航向偏差和舵机能耗。

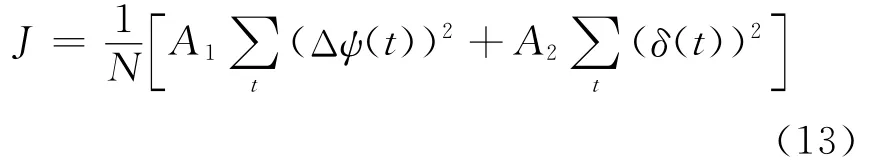
其中，A1和A2分别为航向偏差和舵机能耗的权值；δ（t）为实时舵角；N为采样次数，可反映实验时长。

同样利用问卷对船舶驾驶员进行调查，在使用航向自动舵进行航向保持时，如果船舶发生偏离设定航向时，在减少航向偏差和尽量减少舵机能耗2项内容中进行选择，得到减少航向偏差次数为43，减少舵机能耗次数为15。

根据统计可以得出保向精度指标权重为：

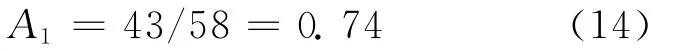
舵机能耗指标权重为：

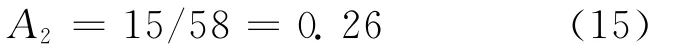
3 航向控制算法的实现

算法的实现首先要根据当前的船舶参数及环境信息，确定此时航向控制算法的3个参数Kp、Ki、Kd的初始值。关于λ的取值，Koyama建议取8～10，而Norrbin建议取0.1，前者在恶劣的海况下有很好的控制效果，后者在平静海域效果非常理想［8］。以此为据，本文初步尝试确定λ的取值见表2所列。

表2 λ与风速对应的取值

根据设定的环境因素，确定当前环境下λ的取值，计算出船舶在当前环境中Kp、Ki、Kd初始值。船舶的计划航向可通过手动设定，而实时航向可以通过SIHC仿真研究平台获取，进而可以分别求出航向偏差和航向偏差变化率并进行模糊化处理，通过参照 ΔKp、ΔKi、ΔKd的模糊控制规则表［8］，即可以得到 ΔKp、ΔKi、ΔKd的真值。最后得到模糊自整定PID控制算法中的Kp、Ki、Kd的值［9］，算法会输出相应的舵角命令，控制船舶达到计划航向并保持稳定。

4 船舶智能操控仿真测试平台应用

将研发团队近20年研究形成的船舶拟人智能避碰决策（PIDVCA）理论［10］应用于平台的智能化研究与实现上，即搭建船舶智能操控（SIHC）仿真测试平台［11］，平台特点包括智能目标船功能、先进的仿真技术、集成6自由度液压／电动平台、接入AIS交通流功能、标准电子海图平台，船舶集成了丹麦航海研究所（DMI）开发的6自由度船模。此平台是用于船舶航行自动化基础研究的仿真测试平台，其中船舶具有航向和航迹2种自动控制模式，能实现船舶自动避碰与航迹自动监控，可用于船舶智能避碰决策算法与智能控制算法测试，为本文系统软件的测试提供了近似海试环境，且比海试环境更具灵活性、快速性、安全性及经济性。为便于仿真测试，在实际仿真平台中仅采用桌面版的形式，即只保留船模仿真、电子海图综合显示模块和智能辅助决策支持模块。

5 航向控制算法的仿真

实验1 航向跟踪仿真。在SIHC平台上分别设置环境条件为无风浪以及不同风浪等级，船舶的初始速度均为其服务速度，初始航向为0°。在船舶开始运行时，将其车钟都推到FULL挡，分别调用优化前、后的模糊自整定PID航向控制算法控制本船由初始航向转到60°航向，当船舶航向达到60°并保持稳定时，结束本次实验。

由于从仿真效果图中难以看出2种算法控制效果的差别，借助控制台导出实验数据，利用Matlab软件分别绘制上述实验船舶的航向及舵角的变化曲线，如图1所示。由图1可知，优化后的航向跟踪速度较快且大幅度操舵持续时间短，航向跟踪性能及能耗均有所改善。

实验2 航向保持仿真。分别设置环境条件为不同风浪等级，在电子海图中添加1条船舶，设置船舶的初始速度均为其服务速度，初始航向为60°。在船舶开始运行时，将车钟都推到FULL挡，分别调用优化前、后的模糊自整定PID航向控制算法控制船舶保持当前航向并达到稳定。同样借助控制台导出实验数据，利用Matlab软件分别绘制上述实验中船舶的航向及舵角的变化曲线，如图2所示。

由图2可知，优化前、后船舶的航向保持性差别不明显，需利用航向保持性能评判方法对船舶 航向保持性能进行评判。

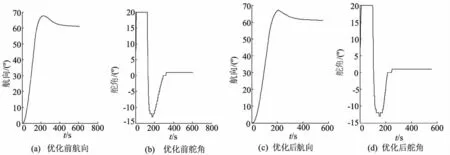
图1 实验1优化前、后集装箱船航向及舵角曲线

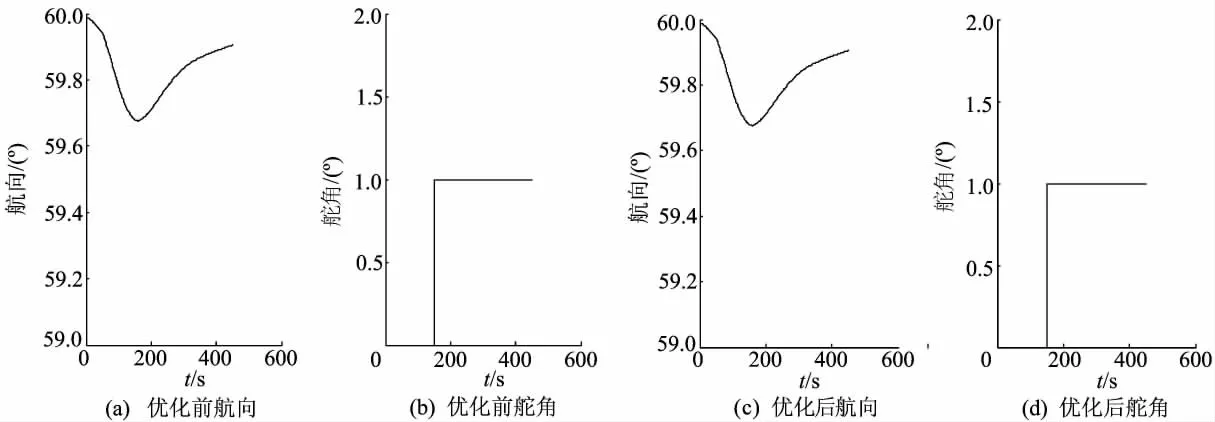
图2 实验2优化前、后集装箱船航向及舵角曲线

6 航向控制算法的性能测试

本文分别设定风向为0°和90°，依次设置不同风速，波浪模式设置为风生浪，分别调用优化前、后的模糊自整定PID航向控制算法控制船模完成航向跟踪及航向保持实验，导出航行数据并绘制航向及舵角变化曲线。利用第2节中介绍的加权综合评判法，分析实验数据得到航向跟踪性能评判的5个指标值。

为了方便比较不同风向及环境等级对算法跟踪性能的影响，本文在对各指标值做无量纲化处理时，其中的指标平均值为2种风向情况下各指标值的平均，最后完成0°与90°风向条件下航向跟踪性能评判。

在测试实验中选用了5条船模I、II、III、IV、V，依次为散货船、集装箱船、油轮、护卫舰以及海军巡逻艇，评判结果分别见表3、表4所列。表中的空格表示在相应环境条件下，优化前、后的算法无法控制完成设定的航向跟踪。

根据航向保持性能评判方法，借助Matlab即可得到0°和90°风向不同环境等级中5条船模的航向保持性能评判结果，分别见表5、表6所列。

表3 0°风向条件航向跟踪性能测试结果

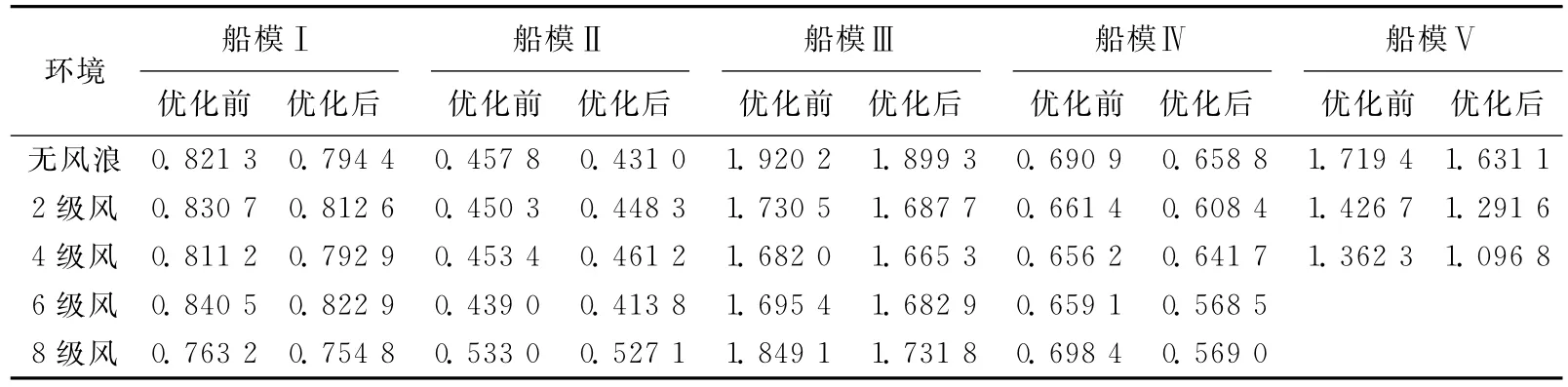
表4 90°风向条件航向跟踪性能测试结果

表5 0°风向航向保持性能测试结果

表6 90°风向航向保持性能测试结果

7 结束语

从评判结果可以看出，船舶在优化的模糊自整定PID航向控制算法控制下的航向跟踪性能评判结果更小，即船舶具有更好的航向跟踪性能。航向控制算法优化后，集装箱船航向跟踪性能最优，其次为护卫舰和散货船。同一船模在不同环境条件下的航向跟踪性能受风向变化以及风速不同的影响不明显，说明算法跟踪性能对环境具有较好的适应性。

从航向保持性能测试结果可以看到，对于多数同样环境中的同一条船模，在优化后的模糊自整定PID航向算法控制作用下，其航向保持性能评判结果更低，即具有更好的航向保持性能。优化前、后的算法对集装箱船的航向保持性能较好，其次为散货船和护卫舰，航向保持性能优劣顺序与航向跟踪性能评判结果一致。

［1］ Zhao Qing，Li Lina，Chen Guoquan.Research on fuzzy selftuning of PID autopilot［C］／／The 3rd International Conference on Transportation Engineering.American Society of Civil Engineers，2011：985－990.

［2］ 汪明慧，余先权，曾 碧.神经模糊控制在船舶自动舵中的应用［J］.计算机应用，2010，30（8）：2261－2264.

［3］ 赵 晴.船舶航迹智能控制算法的研究［D］.厦门：集美大学，2012.

［4］ 蒋丹东.船舶航迹控制［D］.大连：大连海事大学，1997.

［5］ 徐健平.船舶自适应舵的一种算法研究［D］.大连：大连海事大学，2012.

［6］ 韩 轶，唐小我.满足一定分布规律的多指标综合评价方法的优化选择［J］.管理工程学报，1999（3）：55－58.

［7］ 张卫华，赵铭军.指标无量纲化方法对综合评价结果可靠性的影响及其实证分析［J］.统计与信息论坛，2005，20（3）：33－36.

［8］ 周 蓉.船舶航向自适应PID控制器的设计与应用［D］.大连：大连海事大学，2012.

［9］ 李 兵，方 敏，汪洪波.模糊PID液位控制系统的设计与实现［J］.合肥工业大学学报：自然科学版，2006，29（11）：1370－1374.

［10］ 李丽娜，陈国权，邵哲平，等.船舶拟人智能避碰决策方法及其评价标准的构建［J］.大连海事大学学报，2011，37（4）：1－5.

［11］ 蒋 娇，李丽娜，陈国权，等.基于SIHC仿真平台的船舶航向控制算法性能测试［J］.上海海事大学学报，2013，34（4）：13－17.