动压滑动轴承遗传算法优化设计中的参数选择

舒 磊， 王晓红， 孙 军， 宋现浩， 许 枫

（1.合肥工业大学 机械与汽车工程学院，安徽 合肥 230009；2.中国船舶重工集团公司 第七O三研究所，黑龙江 哈尔滨 150078）

动压滑动轴承具有工作平稳、可靠性高和噪音低等特点，是各种机械装置中应用最广泛的流体动力润滑的机械零件，其工作状况对机械装置工作经济性、可靠性和耐久性等性能有非常重要的影响。动压滑动轴承的优化设计是现代机械受人关注的研究领域，其相关研究工作一直在持续不断地进行［1－7］。

动压滑动轴承优化设计的计算规模大，不同轴承类型模型又不相同。本文通过建立轴承性能数据库，调用数据库中数据进行插值计算，应用遗传算法进行动压滑动轴承优化设计。研究发现采用不同参数的遗传算法进行优化时，遗传算法的性能不一致，有时甚至无法得到真实的最优解。针对上述问题，本文根据不同情况，采取不同参数的遗传算法，探讨了参数选择对基于遗传算法动压滑动轴承优化设计结果的影响。

1 动压滑动轴承优化设计模型

1.1 设计变量

取轴承直径d、偏心率ε、间隙比ψ、宽径比λ、预负荷δ和转速n为设计变量，即

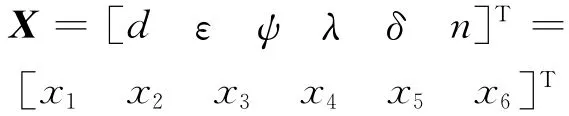
1.2 目标函数

目标函数选取轴承润滑油流量Q，其表达式为：

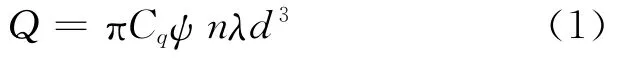
其中，Cq为润滑油流量系数。

1.3 约束条件

（1）轴承最小油膜厚度hmin约束。

其中，［hmin］为轴承的许用最小油膜厚度。

（2）轴承宽径比λ约束。

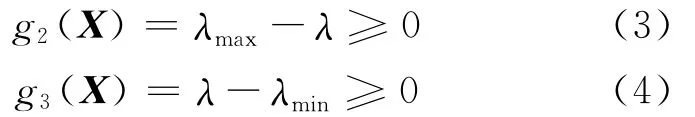
其中，λmin为宽径比λ的最小值；λmax为宽径比λ的最大值。

其中，［p］为轴承的许用比压。

（4）轴承间隙比ψ约束。

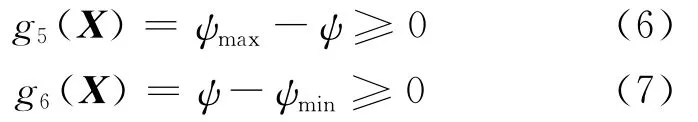
其中，ψmax为轴承间隙比的最大值；ψmin为轴承间隙比的最小值。

（5）轴承润滑油流量Q约束。

其中，［Q］为许用（要求）的轴承润滑油流量。

（6）轴承摩擦功耗Nf约束。

其中，［Nf］为许用（要求）的轴承摩擦功耗。

（7）轴承润滑油温升ΔT约束。

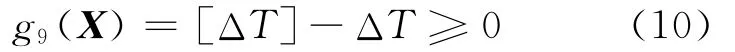
其中，［ΔT］为许用（要求）的轴承润滑油温升。

（8）轴承承载力F约束。

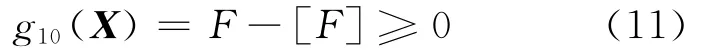
其中，［F］为要求的轴承承载力。

数学模型［8］为：

2 动压滑动轴承优化过程

轴承润滑分析计算十分复杂耗时，优化中需要对不同设计变量通过求解Reynolds［9］方程得到相应摩擦功耗、最小油膜厚度、平均比压、承载力、润滑油流量、润滑油温升和动态特性系数等润滑性能数据，该过程将占很长的计算时间，并且在一次优化过程中要进行数千次的润滑分析计算。本文采用的方法如下：预先确定轴承变量的变化范围并分为若干等分，确定轴承变量的设计点；针对每一个设计点，通过轴承润滑分析计算［10］获得轴承性能数据；所有设计点计算完毕后，建立轴承润滑性能数据库。在进行轴承优化的过程中，以建立的数据库为基础，采用插值方法获取不同设计变量下的轴承润滑性能参数。

3 遗传算法的参数选择

3.1 遗传算法的原理

遗传算法是受生物进化思想启发得出的一种全局优化算法，基本思想是基于Darwin进化论和Mendel的遗传学说。遗传算法从一组随机产生的称为“种群”的初始解开始搜索过程。种群中的每个个体是问题的一个解，称为“染色体”。染色体是一串符号，如二进制字符串。这些染色体在后续迭代中不断进化，称为遗传。在每一代中用“适应度”来测量染色体的好坏［11］，生成的下一代染色体称为后代。后代由前一代染色体通过交叉或者变异运算形成。在新一代形成过程中，根据适应度的大小选择部分后代，淘汰部分后代，保持种群大小不变。适应度高的染色体被选中的概率较高。这样，经过若干代后，算法收敛于最好的染色体，即为问题的最优解［12］。

3.2 遗传算法参数选择分析

遗传算法选择位串长度L、种群个体数、进化代数和变异概率Pm等4个参数［13］。

3.2.1 位串长度

遗传算法采用二进制编码形式进行，优化前对设计变量的取值空间进行确定和编码。在确定取值范围后，空间被均匀划分成若干份，其数量与位串空间内的位串数目相同，每个被划分的取值与1个位串结构相对应。如果位串长度增加，位串数目将增加，与之对应的取值空间划分数目增多，设计变量的取值精度增加，优化结果更精确。通过改变位串长度可以协调搜索精度与效率之间的关系。

以设计变量动压滑动轴承偏心率ε为例，ε的取值范围为0.10～0.95。L取值不同时，对ε范围进行划分的结果见表1所列。其中，N为出现次数。可见，设计变量空间划分份数为2L。L越大，设计变量空间被划分得越细，变量的取值越多且越精确，搜索范围越大，结果越精确。

表1 偏心率取值范围的空间划分

3.2.2 种群个体数

在遗传算法优化设计过程中，种群数起着重要作用。种群个体数越多，初始化的种群个体落在符合约束条件的可行域空间的密度越大，越有可能搜索到最优解。从计算角度，种群的规模越大，需要计算更多的适应度函数，使算法的时间呈指数增长。所以，选定种群规模时，需要综合考虑算法的可靠性和计算时间。一般而言，种群数为30～40时，已经可以搜索到所有的区域，再增加种群数并不能提高算法性能。约束条件较简单，可行域范围较大时，可以增加种群数至100。

3.2.3 进化代数

一般遗传算法优化可以在预设的进化代数之前达到全局最优解，但是有时可能出现种群的某些个体接近局部最优解的情况，导致在预设的进化代数前无法达到种群个体收敛于全局最优解。对于这种情况，建议适当增加进化代数。一般进化代数取30～150。

3.2.4 变异概率Pm

在遗传算法优化设计中，种群的每个个体初始随机生成，约束条件决定种群个体出现的区域。约束条件越多，满足约束条件的可行域越小，符合条件的区域通常互相独立，无规则地分布在整个空间中，最优解所在的区域称为最优区域。初始种群创建后，所有的个体都散落在这些相互独立的区域内。进行进化迭代时，无论约束较多还是较少，所有的个体都根据自身适应度的大小被选择进化或被剔除。每次形成新的子代后，每个子代有一定的变异概率，保证种群的多样性，避免优化结果过早收敛。一般遗传算法的变异概率为0.1。如果约束条件较多，满足条件的区域很小并且相互不连接，若使用较大的变异概率，接近最优区域的个体可能直接跳出最优区域，到达不满足约束的区域，导致无法收敛。如果约束条件少，空间内的可行域比较大，可行范围较广，若采用较小的变异概率，种群的变异将比较少，变异后数据的变化量比较小，往往需要多次进化变异才能接近最优解，导致算法的计算效率下降，计算时间增加。本文建议通常情况下按0.05≤Pm≤0.10进行计算，当所得的结果无法收敛或无法达到设计要求，可以适当减小Pm。

4 优化实例

为了验证变参数遗传算法应用于动压滑动轴承优化设计问题的有效性，以圆轴承为例进行计算分析比较。圆轴承参数如下：直径0.05m，轴承转速1 000r／min，目标函数为润滑油流量。各约束条件：轴承载力为300N，许用最小油膜厚度hmin为0.02mm，宽径比最小值为0.6，宽径比最大值为1，许用比压为0.21MPa，间隙比最小值0.001，间 隙 比 最 大 值 0.002，许 用 流 量 为0.04L／min，许用摩擦功耗为0.04kW，许用润滑油温升为30℃。

种群个数为30，采用不同变异概率进行优化的结果见表2所列。变异概率为0.05时，采用不同种群数进行优化的结果见表3所列。变异概率为0.05，种群个数为30时，采用不同位串长度进行优化的结果见表4所列。

从表2可知，在相同的约束条件下，变异概率为0.10的遗传算法优化得到的润滑油流量最优值范围为0.033 4～0.035 1L／min，变异概率为0.05和0.01的遗传算法优化的最优值范围分别为0.033 3～0.034 7L／min 和 0.033 3～0.034 3L／min。与变异概率为0.10的优化结果相比，变异概率为0.05和0.01的优化将最优解值精度提高了0.8%，都可以得到最优解0.033 3L／min。变异概率为0.05优化的最差解为0.034 7L／min，变异概率为0.01优化的最差解为0.034 3L／min，变异概率为0.01的优化解更加逼近真实的最优解。另外，变异概率为0.01的优化结果集中在一个更小的范围内，优化结果的波动比其他2种变异概率小，优化结果更加稳定，得到最优解的概率更大。

从表2、表3可知，在相同约束条件下，采用不同种群数，相同变异概率的遗传算法优化得到的最优解情况有所不同。种群数为30时10次优化计算2次得到最优解为0.033 3L／min，种群数为60时10次优化计算4次得到最优解为0.033 3L／min，种群数为100时10次优化计算6次得到最优解0.033 3L／min。因此，采用较大的种群数可以增大得到最优解的概率。

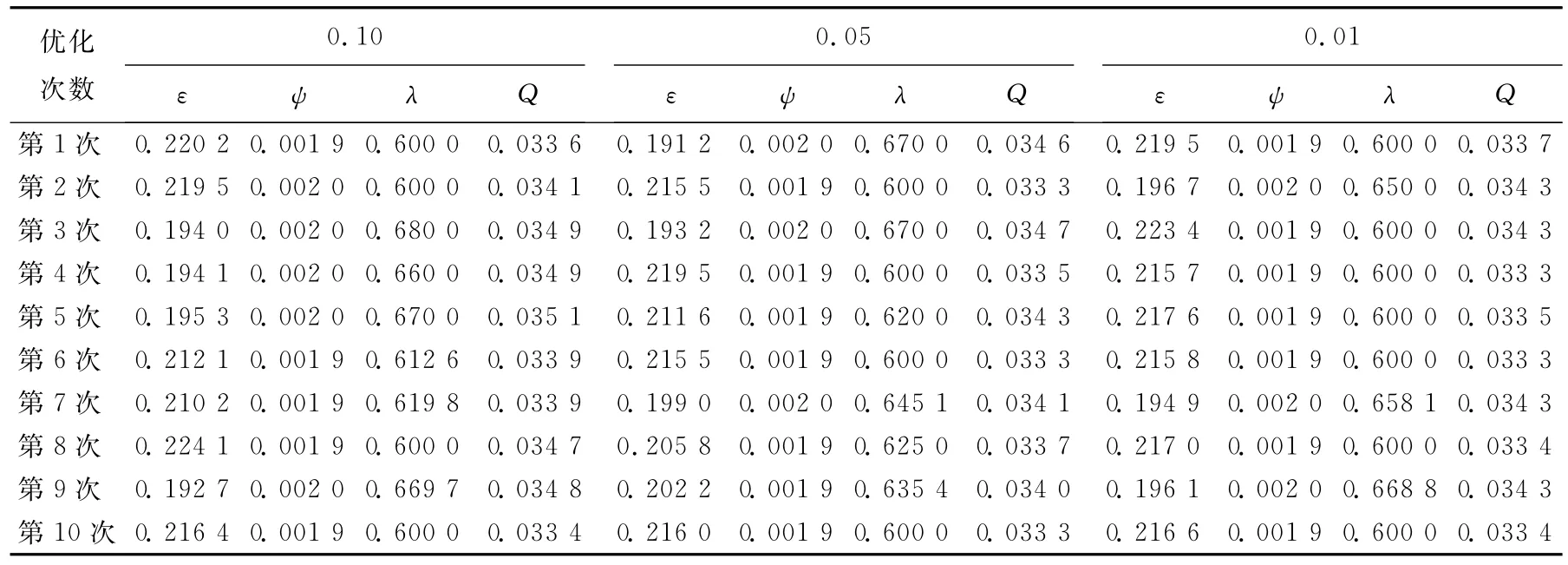
表2 种群个体数为30，不同变异概率下的优化结果

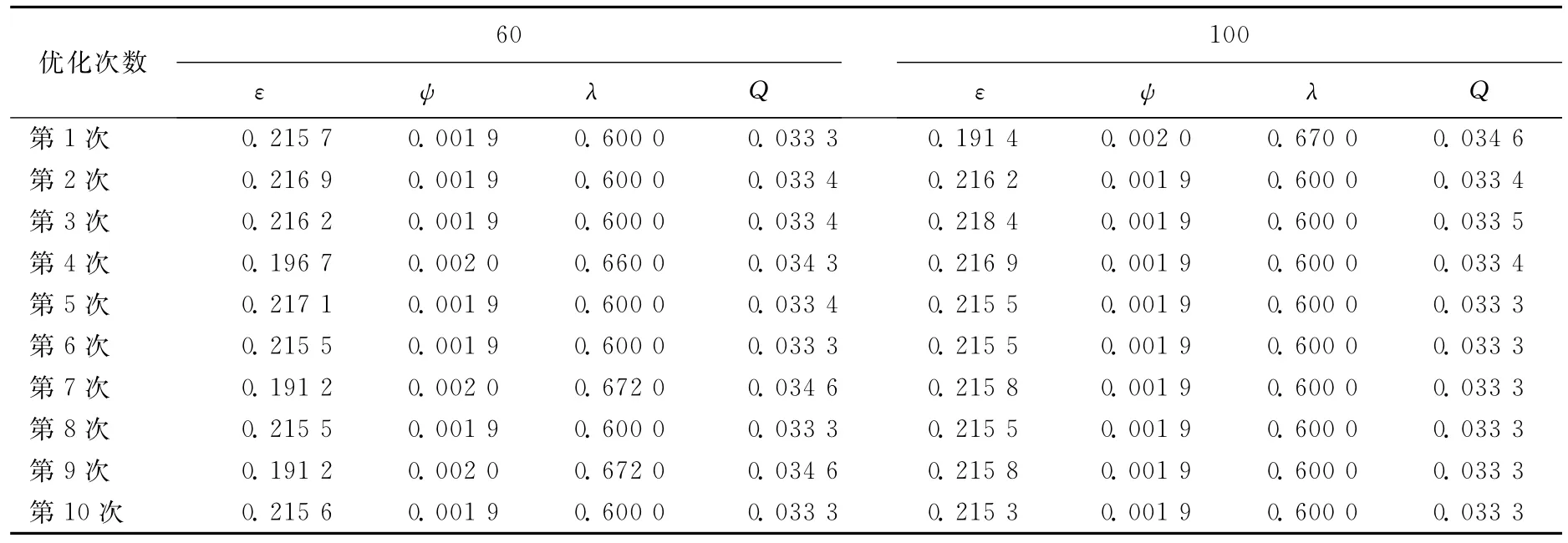
表3 变异概率为0.05，不同种群个体数下的优化结果

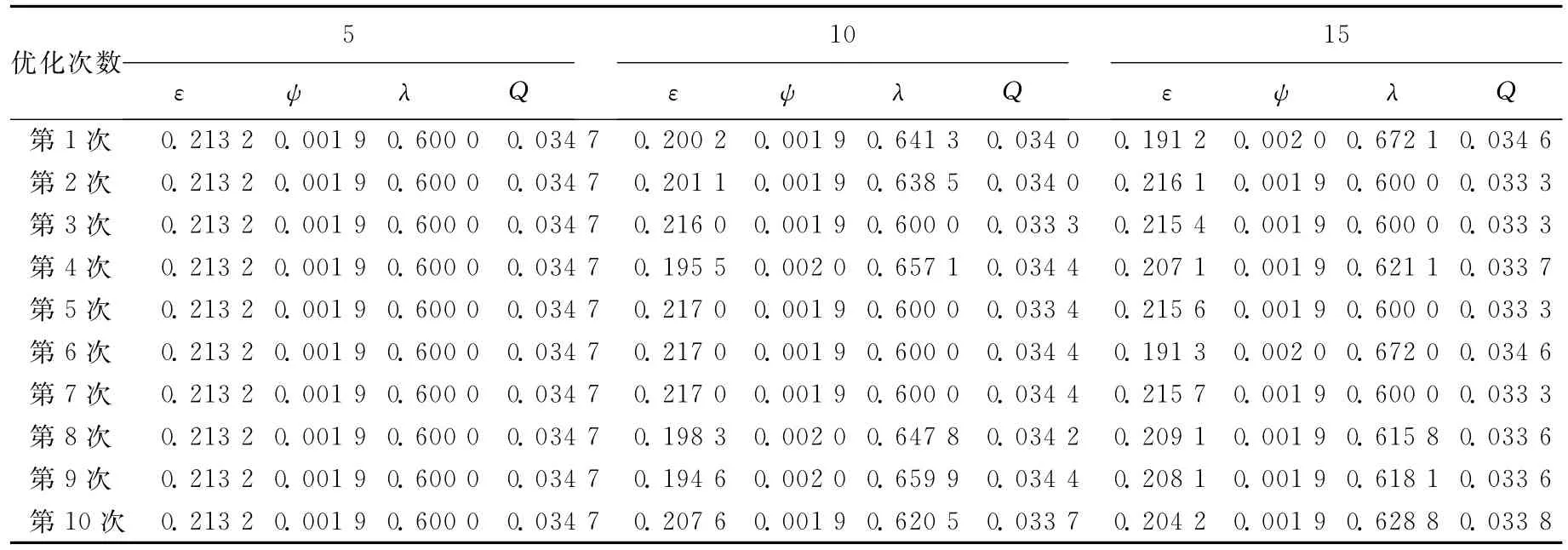
表4 变异概率为0.05，种群个体数为30，不同位串长度下的优化结果

从表4可知，在相同的约束条件下，位串长度 为5时优化得到的最优解为0.034 7L／min，位串长度为10和15时优化得到的最优值范围分别为0.033 3 ～ 0.034 4L／min 和 0.033 3 ～0.034 6L／min。位串长度为5的优化由于设计变量范围被划分得少，搜索范围小，导致其最优解只能为0.034 7L／min；位串长度为10和15的优化得到的最优解范围基本一致，但是位串长度为10的优化解大部分为0.034 0～0.034 4L／min范围内，而位串长度为15的大部分优化解范围在0.033 3～0.033 6L／min，更接近于最优解。因此，位串长度越长，得到最优解的概率越大，结果越稳定。

综上所述，在约束条件较多时，采用较小的变异概率有利于优化结果逐步逼近或得到真实的最优解，得到真实最优解的概率上升，但是不能确保每次优化结果都得到真实的最优解；如果约束条件并非十分复杂、可行区域互相不分散，遗传算法的种群数不需要太大，通常取30～60；遗传算法的位串长度主要根据计算精度和设计变量的范围设置，在一定范围内，位串长度越长，搜索范围越大，得到最优解的概率越高，但是位串长度过长会降低计算效率，通常取10～20。

5 结束语

在约束条件较多的情况下，减小变异概率可以有效地改进遗传算法优化设计结果。选定种群个体数时，应综合考虑算法的可靠性和计算时间。对于一些特殊情况，建议适当增加进化代数，保证在预设进化代数之前优化收敛于全局最优解。位串长度决定于设计变量范围的划分份数，影响搜素范围和结果的精确程度。

遗传算法是一种全局随机搜索方法，对遗传算法参数的控制只能增大获得最优解的概率和结果的稳定性，不能保证每次优化都获得最优解。本文提出的动压滑动轴承遗传算法优化设计参数选择确定方法可以拓展到基于遗传算法进行优化设计的其他领域。

［1］ Li Yuansheng，Li Lei，Yu Ming，et al.Adaptive multi－objective optimum design of journal bearing based on a backstepping approach ［J］.Tribology Transactions，2012，55（1）：12－19.

［2］ Zengeya M，Gadala M.Optimization of journal bearings using a hybrid scheme［J］.Proc Instn Mech Engrs Part J：Journal of Engineering Tribology，2007，221（5）：591－607.

［3］ Hirani H.Multiobjective optimization of a journal bearing using the Pareto optimality concept［J］.Proc Instn Mech Engrs Part J：Journal of Engineering Tribology，2004，218（4）：323－336.

［4］ Boedo S，Eshkabilov S L.Optimal shape design of steadily loaded journal bearings using genetic algorithms［J］.Tribology Transactions，2003，46（1）：134－143.

［5］ Yang B S，Lee Y H，Choi B K，et al.Optimum design of short journal bearings by artificial life algorithm ［J］.Tribology International，2001，34（7）：427－435.

［6］ 庞晓平，陈 进，王家序.采用通用膜厚方程的动压径向轴承形状优化［J］.西安交通大学学报，2009，43（1）：57－61.

［7］ 黄保科，孙 军，王 虎，等.发动机曲轴轴承的多目标综合优化［J］.汽车工程，2012，34（9）：842－846.

［8］ 刘惟信.机械最优化设计［M］.第2版.北京：清华大学出版社，1994：10－11.

［9］ 温诗铸，黄 平.摩擦学原理［M］.第3版.北京：清华大学出版社，2008：21－27.

［10］ 蔡晓霞，孙 军，桂长林.考虑热效应的轴颈倾斜轴承润滑分析［J］.合肥工业大学学报：自然科学版，2008，31（10）：1590－1593.

［11］ 曹祝君，吴国凤.一种改进的遗传算法［J］.合肥工业大学学报：自然科学版，2004，27（9）：1070－1073.

［12］ 王小平，曹立明.遗传算法：理论应用与软件实现［M］.西安：西安交通大学出版社，2002：4－14.

［13］ 张文修，梁 怡.遗传算法的数学基础 ［M］.第2版.西安：西安交通大学出版社，2003：10－29.