混合算法在钢构企业生产调度系统中的应用

雷兆明，佟静翠 ，花季伟，郭子超

（1.河北工业大学 控制科学与工程学院，天津 300130；2.天津师范大学 计算机与信息工程学院，天津 300387）

企业的生产管理系统越来越受到企业的广泛关注，而合理的生产调度系统是保证企业长期规划顺利、顺畅实施的关键所在[1]。因钢结构产品的很多优点而在各方面得到广泛使用，从而带动钢构企业迅速发展。如何提高企业生产效率、减少劳力和机械损耗已成为现代钢构企业追寻的目标。

Job-Shop调度是一种复杂的组合优化问题和典型的NP难题[2]。文献[3-4]等都提出过关于柔性Job-Shop调度问题的求解方法。本文结合钢结构的实际生产特点与约束条件，在生产计划调度系统中建立了多目标生产数学模型，用基于蚁群遗传混合算法进行求解，并通过方案对比得出了该生产调度系统的高效性、可执行性。

1 系统功能设计

对钢构企业而言，如何面向多品种小批量的大量订货合同而组织生产是生产管理系统面临的最大困难。因为生产计划指导着关键生产环节的进行，它必须考虑到生产过程中的实际因素，如不同钢种、规格和交货期需求，多班组工序分配等。

生产调度是将生产基于订单合同的生产顺序计划解析成为设备、原料等生产资源的分配依据，以客户需求为目标，结合企业产能和工艺流程约束，对企业的生产资源进行调度分配，以节约生产时间、提高企业利润为目标，指导生产活动有序进行[5]。生产计划与调度在生产系统中的位置关系及信息流动如图1所示。

2 关键算法

钢构企业的工序多班组选择调度问题属于柔性作业车间调度问题。针对该问题，本文提出了通过蚁群遗传混合算法来实现生产调度的优化选择，最终使企业生产系统相关性能指标最优，如总完工时间、生产能力与负荷均衡。

2.1 问题描述与建模

工序多班组选择调度问题可描述为N个工件在M个班组上加工，每个工件至少含一道工序，预先给出工件工序的加工顺序，每道工序可由至少一个班组加工，且同一道工序在不同班组上加工工时不同，该作业调度的目标是为工件的每道工序确定合适的班组，完成所有工序的先后加工时间，使各班组的生产能力与负荷均衡，使生产系统完成总任务的时间最短。

根据调度模型需对生产过程做如下假设：

1）工序一旦开始就不能中断；

2）大型公共设备运输工序的时间考虑在加工时间范围内；

3）同一种工件的工序间加工优先级不同，不同工件间的工序加工顺序优先级相同；

4）工序在班组上的加工时间是预先给定的；

5）同一工件的工序在同一时刻只能在一个班组上加工，同一时刻一个班组只能加工一个工件。

以下是数学模型中参数和变量的说明：N为工件总数；m为班组总数；Ω为总的班组集；i为班组序号，i=1，2，3…m； j，k 为工件序号， j，k=1，2，3…n；TOj为工件j的总工序数；Ojx为工件j的第x道工序；Xijx为工件j的第x道工序在i上加工；tijx为工件j的第x道工序在i上加工时间；Sjx为工件j的第x道工序加工开始时间；Ejx为工件j的第x道工序加工结束时间；Cmax为最大完成时间。

柔性路径选择调度模型必须满足的约束：

1）每一个工件工序的加工具有优先级，则

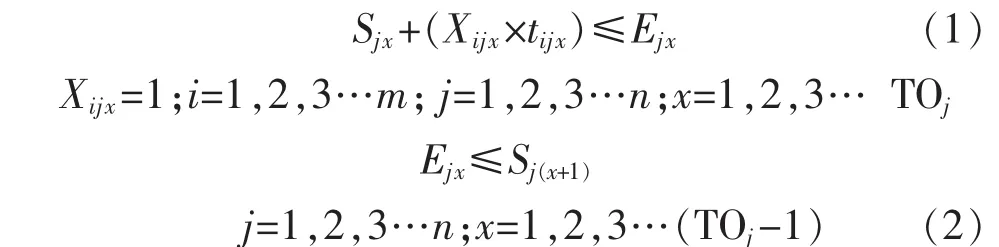
2）任一确定时刻，班组i不能同时加工2个不同的工件，也不能同时加工2道不同的工序，则：

多目标优化问题数学模型描述：

给定决策向量 X=（x1，x2，…，xz），满足的约束条件为

其中：g为q维向量函数；h为p维向量函数；设有t个相互冲突的优化目标，可表示为

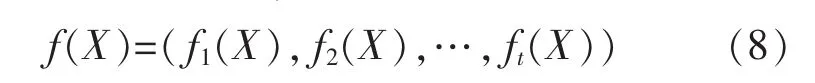
则 f为 t维向量函数。 求 X*=（x1*，x2*，…，xz*），使f（X*）在满足式（6）和式（7）条件下的目标达到最优。为便于求解，将所有优化目标表示为最小化函数，即：

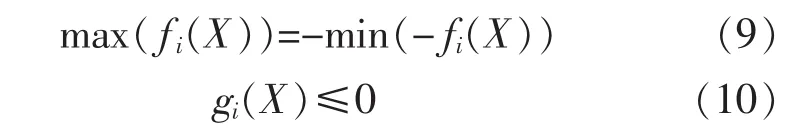
因此目标优化问题的统一表达形式为

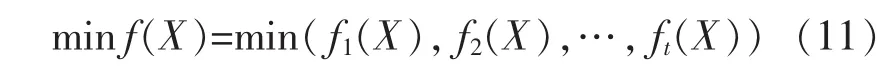
多目标生产模型的建立：

在满足上述条件的前提下，可对调度模型中的工件进行调度，从而确定工件的加工设备，及在设备上的开工时间。考虑生产调度中涉及多个目标函数，建立的调度模型：

1）工件最大完工时间最小

2）瓶颈设备负荷最小

3）设备总负荷最小

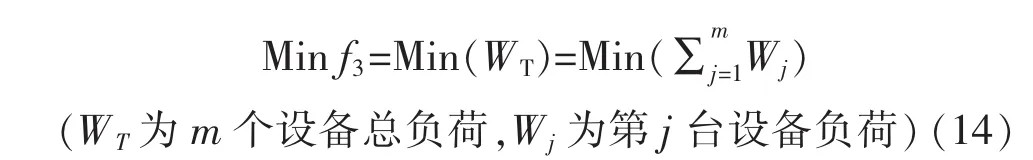
所以建立多目标调度问题的数学模型可表达为

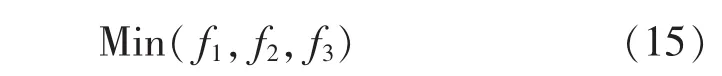
2.2 钢构件工序在多班组中调度的关键算法

图2 混合算法结构Fig.2 Hybrid algorithm structure

2.3 工序可选班组析取图模型

采用蚁群优化算法求解FJSP中工艺路线问题，首先将该问题表示成易求解的解构造图模型，即建立工件各工序可选加工班组析取图模型，然后将其进一步描述为有向图G=（V，C∪D）（V为所有节点的集合，C为有向图G中所有有向弧的集合，D为有向图G屮所有析取边的集合）。假设工件数、工序数及在各班组上的加工时间已知，则析取图模型和有向图分别如表1和图3所示。

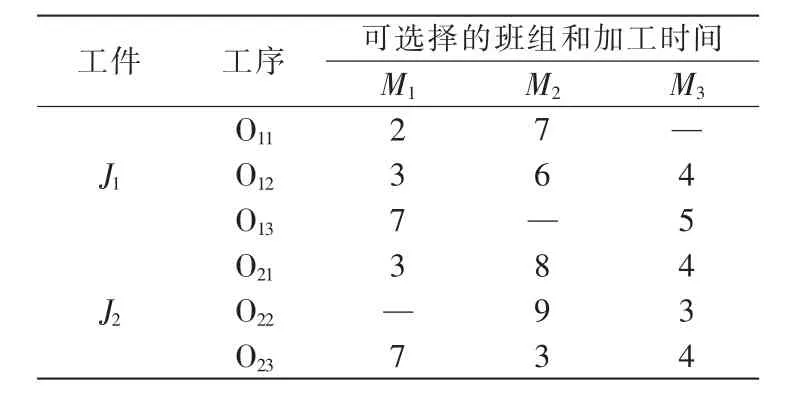
表1 析取图模型Tab.1 Disjunctive graph model

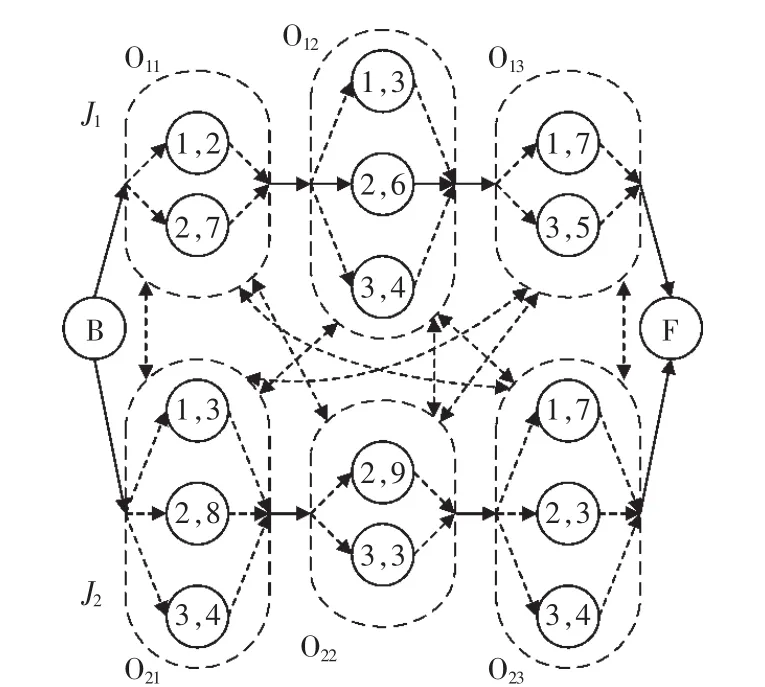
图3 析取图模型Fig.3 Model of disjunctive

2.4 基于蚁群算法班组分配规则

由析取图G=（V，C∪D）可设计蚂蚁的解构造图G=（V，C∪D，τ），τ为信息素分布， 代表弧对解质量的影响。根据图3中析取图模型，可做出工件J1的解构造图，如图4所示。为了便于蚂蚁游历，解构造图中还标注出了局部启发式信息，启发式信息将在后续中介绍。

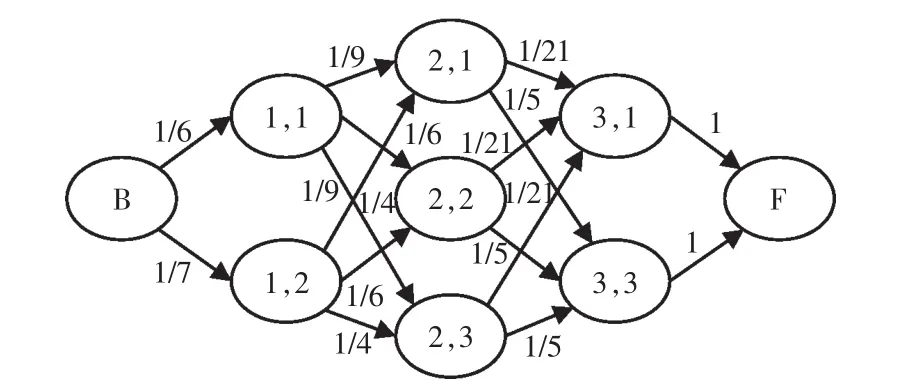
图4 工件J1的解构造Fig.4 Construction of J1piece

为了能够提高算法解的质量和缩短搜索时间，本文将采取最短加工时长班组优先被选中策略。并在班组选择过程中将每个班组已负载的加工时间进行累计，来使班组工作负荷达到平衡。设每个班组已负载的加工时间累计为CMsum，则班组的分配步骤为

1）设置班组负荷矩阵CMsum为1×3的矩阵。每一列分别为M1，M2，M3的总负荷。将该矩阵初始化为［0，0，0］。

2）首先选择工件J1的工序O11，可选班组为M1，M2。选择最短加工时长班组M1，则班组负荷矩阵变为 CMsum=［2，0，0］。

3）再选 J1的工序 O12，可选班组为 M1，M2，M3。选择最短加工时长班组M1，则班组负荷矩阵变为CMsum=［5，0，0］。

4）再选 J1的工序 O13，可选班组为 M1，M3。 选择最短加工时长班组M3，则班组负荷矩阵变为CMsum=［5，0，5］。

5）以此类推，再分别选择工件J2的工序O21、O22、O23，则对应的班组负荷矩阵分别为［8，0，5］［8，0，8］［8，3，8］。

2.5 蚁群算法启发式信息设计

局部启发式信息η的作用是指引蚂蚁选择加工时间最短的班组，从而有利于总负荷和调度方法的最优化，同时还指引蚂蚁选择已承载负荷少的班组，来使班组间负荷均匀分配。根据分配规则，确定路径启发式信息：ηij=1/（CM（1+CMsum）），CM为选择 M班组的负载，CMsum为选择M班组时累计负载。启发式信息数值可见图4的解构造图。工件工序间转移规则为

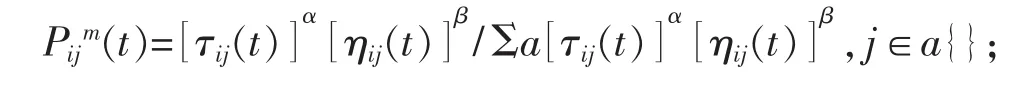
其它情况 Pijm（t）=0。

式中：Pijm（t）为 t时刻蚂蚁 m 选择（i， j）路径的概率；τij（t）为 t时刻选择（i， j）路径的信息素数量；a 为蚂蚁游历下一道工序时的班组集。

3 软件实现

工序多设备选择调度属于柔性作业调度，本文采用封闭式蚁群-遗传混合算法进行求解。首先采用蚁群算法解决工序班组选择问题，从而确定待加工工件相关工序的优选班组；然后采用遗传算法求解基本班组调度问题。其工作流程如图5、图6所示。相关参数设置：蚁群算法参数借鉴文献[6]，迭代数Nc=50、蚂蚁数m=8、启发式因子重要程度参数β=5、信息重要程度参数α=1、信息素挥发率ρ=0.3、信息素增强度系数Q=6，遗传算法参数借鉴文献[7]，群体大小50、迭代次数maxGen=40、交叉因子pxover=0.85、选择算子psel=0.1、变异因子pmutation=0.2。

图5 遗传算法流程图Fig.5 Flow chart of genetic algorithm

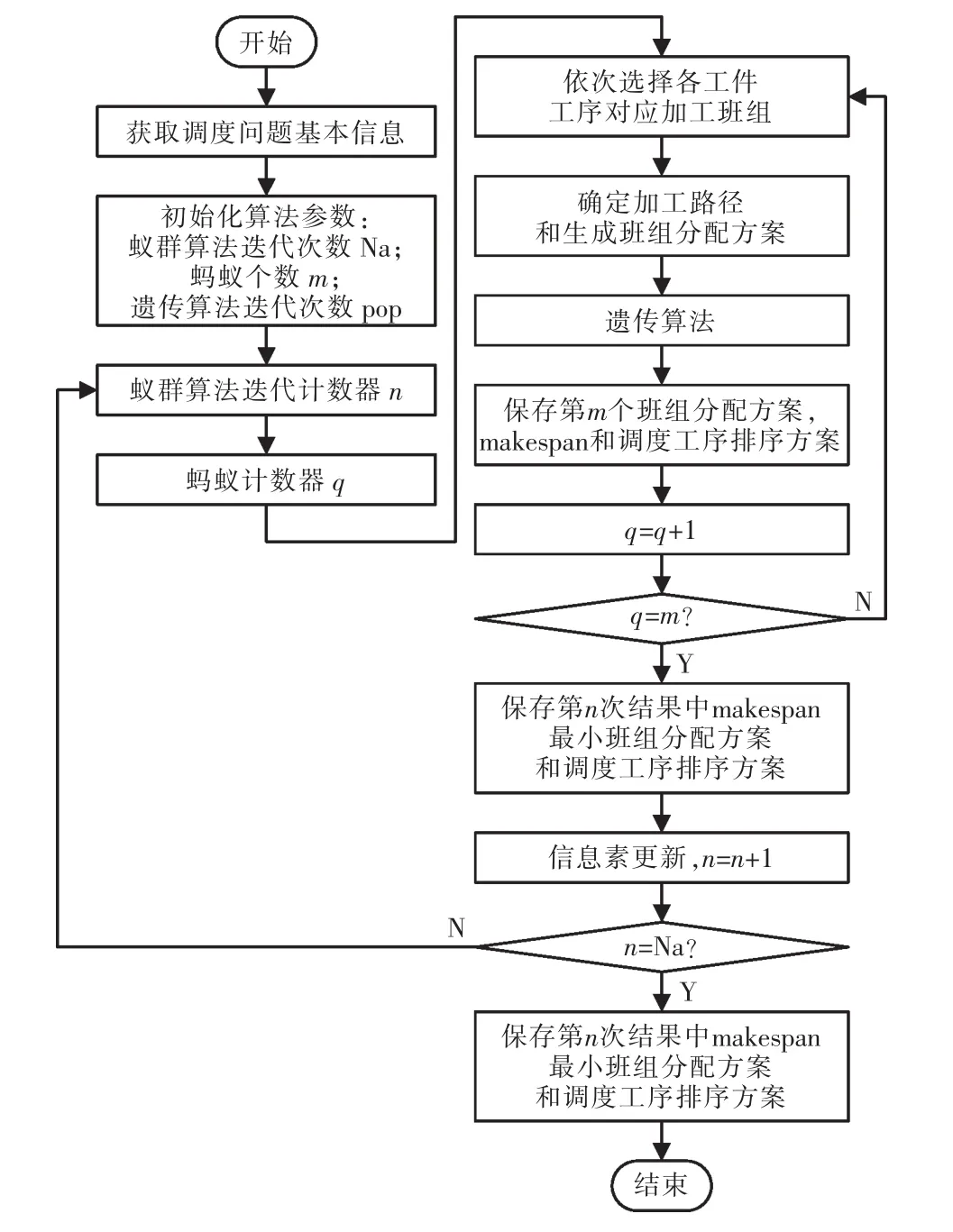
图6 蚁群遗传算法流程图Fig.6 Flow chart of ant colony genetic algorithm

4 应用与结果分析

以表1中工件工序的可加工分布情况为例，将本文提出的蚁群遗传混合优化算法应用于其中，通过编程进行实现。经过优化排序得到工件工序最终加工顺序，如表2所示。

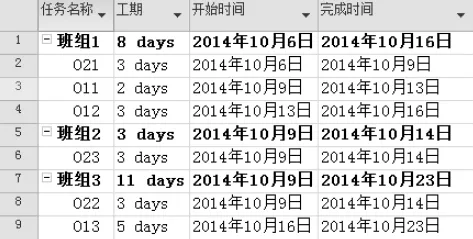
表2 工件工序加工顺序Tab.2 Order of workpiece machining processes

由加工顺序生成的甘特图如图7所示。

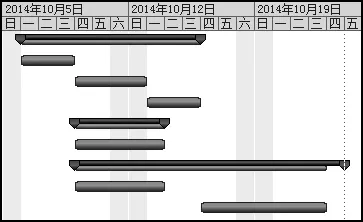
图7 排产甘特图Fig.7 Scheduling Gantt

若不使用该方法进行排产，得到工件工序加工顺序如表3所示。

表3 工件工序加工顺序Tab.3 Order of workpiece machining processes

生成相应的排产甘特图如图8所示。

由图7和图8的排产甘特图对比可知，通过蚁群遗传混合算法优化得到的排产方案要优于不用此方法的排产方案，可提前3个工作日完成工作任务。

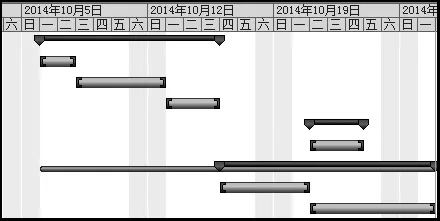
图8 排产甘特图Fig.8 Scheduling Gantt

5 结语

本论文讨论的是工序多设备选择调度的柔性作业问题，建立柔性作业的工序约束和生产调度模型。在算法中着重讨论了班组分配问题，并提出通过蚁群遗传混合算法来解决该问题。应用结果表明该方法是有效的。下一步将优化算法中的相关参数，以进一步提高分配效率。

[1]黄肖玲，柴天佑.复杂生产过程计划调度级联模型在选矿MES中的应用研究[J].自动化学报，2011，37（9）：1130-1139.

[2]Kacem I，Hammadi S，Borne S，et al.Pareto-optimality approach for flexible Job-Shop scheduling problems：hybridization of evolutionary algorithms and fuzzy logic[J].M Athematics and Computers in Simulation，2002，60（3-5）：245-276.

[3]张维存，郑丕谔，吴晓丹.基于蚁群粒子群算法求解多目标柔性调度问题[J].计算机应用，2007，27（4）：936-938，941.

[4]夏蔚军，吴智铭.基于混合微粒群优化的多目标柔性Job-Shop调度[J].控制与决策，2005，20（2）：137-141.

[5]邓宇巍.热轧带钢生产调度模型与算法研究[D].上海：上海交通大学，2007.

[6]CARLIER J，PINSON E.Adjustment heads and tails for the job shop scheduling problem[J].European Journal of Operational Research，1994，78（3）：146-161.