额定功率下光伏发电系统的功率控制研究

丁 陆，邓秋玲,陈 可,谢吉堂

(湖南工程学院 电气信息学院，湘潭 411101)



额定功率下光伏发电系统的功率控制研究

丁 陆，邓秋玲,陈 可,谢吉堂

(湖南工程学院 电气信息学院，湘潭 411101)

通过对光伏电池的分析，应用Matlab/simlink仿真软件工具，建立了光伏电池的数学模型和仿真模型.基于此模型，针对光伏发电系统效率低的问题，研究了在额定条件下光伏发电最大功率跟踪问题.分别对最大功率跟踪控制的两种方法PID控制与改进扰动法控制进行了仿真，并分析了这两种方法各自的优缺点.仿真结果表明，PID控制的振荡小，而改进扰动法的效率更高.

光伏发电；最大功率跟踪；PID控制；改进扰动法控制

0 引 言

对新能源的利用是21世纪全球的一个重大课题，近年来光伏发电和风力发电两种新能源发展迅速.随着社会的发展，分布式发电技术的应用也会越来越广泛，而光伏发电、风力发电等是分布式发电系统的重要组成部分[1].因此，对新能源的研究的重要性日益突出.光伏发电经过近年的发展开发较为成熟，相对风力发电来说光伏发电在某些方面具有自身的优势，比如前期建设投资相对较少、运行维护方便等，但光伏电池的转换效率低， 所以对光伏发电系统的输出功率跟踪控制是必不可少的.本文基于Matlab/simlink仿真软件工具，并在建立起光伏电池仿真模型的基础上，在额定条件下，分别用传统PID控制和目前应用广泛的扰动法控制对光伏发电系统的最大功率进行了对比仿真.最后对这两种控制算法的优缺点进行了分析并做出展望.

1 光伏电池模型与输出特性

1.1 光伏电池模型

光伏电池发电原理是根据半导体的光生伏打效应，由光照产生光生电流.等效电路如图1所示.

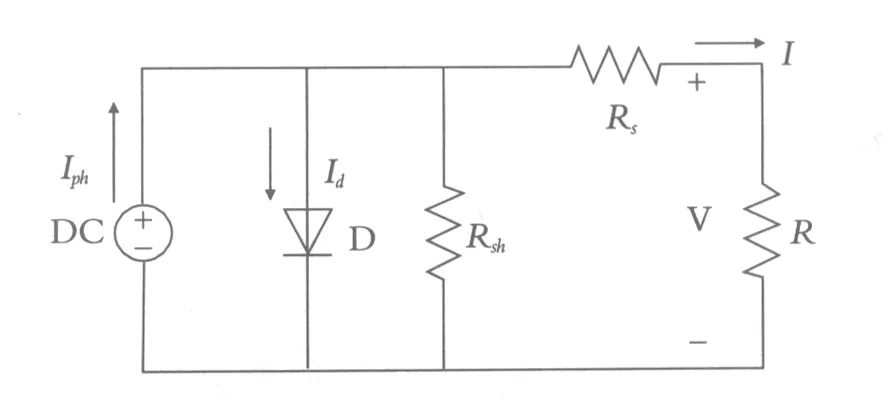
图1 光伏电池等效电路

由电路图可知输出电流与各参数的关系如[2]：

(1)

式中：I是太阳能电池的输出电流；Iph是太阳能电池的光生电流；Id是流经二极管电流；I0是 二极管反向饱和电流；Ish是流过并联电阻Rsh的电流；Rs是太阳能电池串联等效电阻；q是电池组电子电荷(q=1.6×101-9C )；U是电池输出电压；n是二极管的因子；k是波尔兹曼常数(k=1.38×10-23J/K)；T是电池温度(标准状态下25 ℃).

(2)

通过对太阳能电池模型的分析推理，在不同条件下的相关公式如下[3]：

(3)

(4)

(5)

(6)

(7)

(8)

1.2 光伏电池模型仿真与输出特性

由上述数学模型可在Matlab/simlink中建立光伏电池的仿真模型，仿真模型如图2所示，通过对仿真模型参数的设置进行仿真，可得到光伏电池在不同条件下的输出特性.

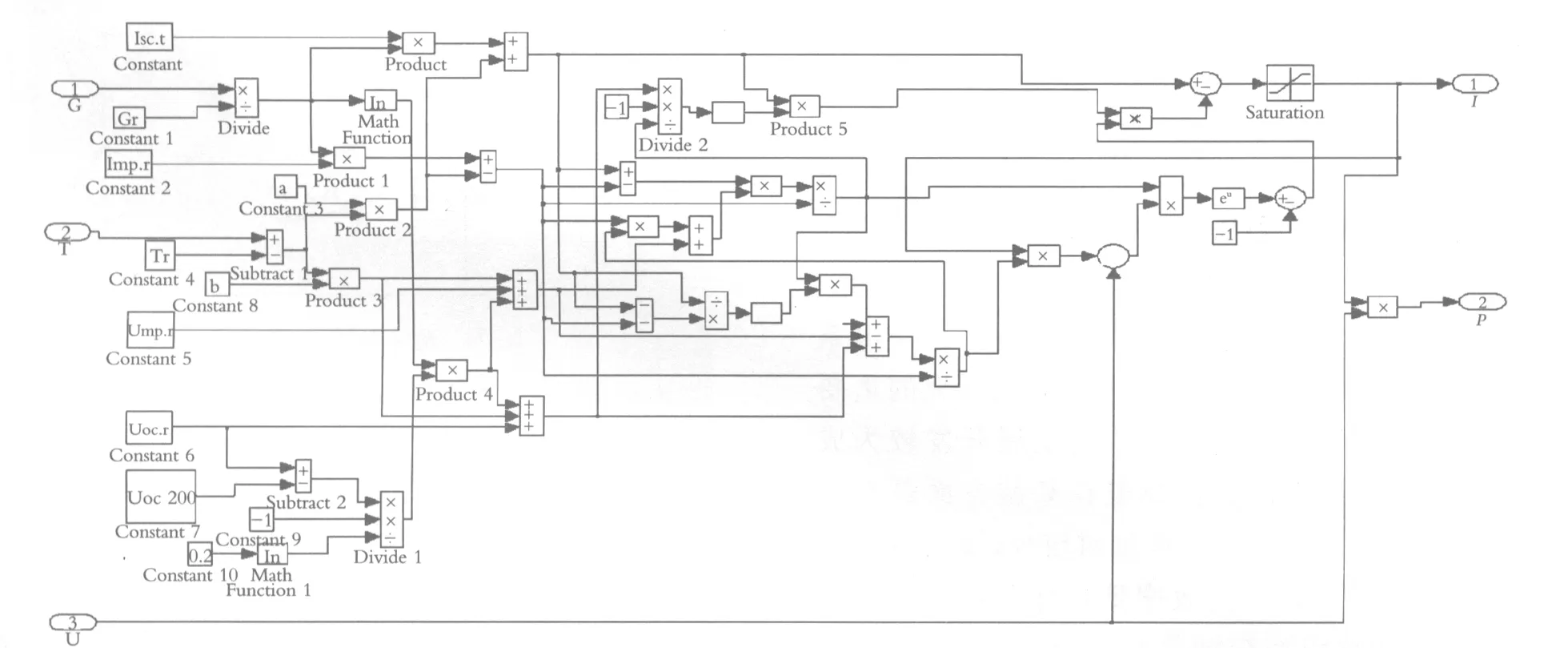
图2 光伏电池仿真模

图中T是温度，G是光照强度，Tr、Gr、Imp.r、Isc.r、Ump.r、Uoc.r、Uoc200分别是标准条件下(光照强度为1000 W/m2，温度为25 ℃)的参数.为便于仿真，对光伏电池进行封装，封装模块如图3所示.

图3 光伏电池封装图

在T=25 ℃时，不同光照强度下的输出特性曲线如图4所示.

图4 T=25 ℃时，不同光照强度

当光照强度不变时，不同温度下的输出特性曲线如图5所示.

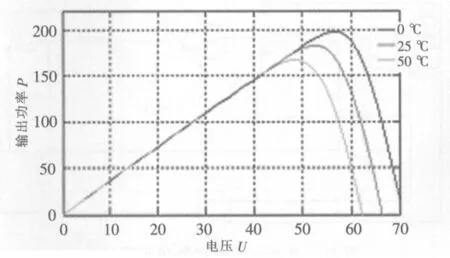
图5 光照强度G=1000 W/m2 时，不同温度下光伏电池P-U特性曲线

由图5可知，在温度为298 K时，不同光照强度下光伏电池的输出功率与光照强度是成正比.在光照强度一定，温度变化时，随着温度的升高，光伏电池的输出功率减小.从图5的分析可知，在已知开发商所提供的数据的前提下，本文所建的光伏电池模型可以很好的对光伏电池输出特性进行描述，该模型可以做为对光伏发电系统仿真分析的使用模型.

2 最大功率跟踪控制

通过图4与图5可知，在不同条件下系统输出功率均不同，但总存在有一点输出功率最大，这一点就是最大功率点.为了使光伏发电系统能够工作在最大功率点上而提出的一系列算法就是最大功率跟踪控制算法.最大功率跟踪算法就是在发电过程中，不管在何种情况下，总是以输出最大功率为目标，通过对这一过程跟踪控制而实现输出最大功率.光伏发电系统的转化效率低(目前国内最高20.5% )，因此对最大功率的输出问题也显得极其重要最大功率点随外界条件变化而变化，在不同的功率点处的电压值也是不同的，所以对最大功率点的控制研究是十分必要的.

目前，在额定情况下，对光伏发电系统的最大功率控制主要有恒电压法、电导增量法、扰动观察法[4].根据戴维宁理，当外部等效电阻与内阻相等时输出功率最大，这几种最大功率控制方法均是通对控制外围斩波电路开关管的开通与关断，从而调节外部电阻与内阻相等以达到最大功率输出的目的.不同的光照和负载条件采取的跟踪方法也不同，若输出功率超过额定值则采用负载跟踪法[4]，这里只讨论额定值以下的跟踪方法.本文主要讨论了PID与扰动法两种最大功率控制的仿真.PID控制是传统控制方法，控制算法成熟，但在非线性系统中很少应用.

2.1 PID控制

上述功率跟踪控制方法中，相对于PID控制而言，有功率损失或成本过高.PID控制应用广泛，发展成熟，且控制效果好，稳定性强.PID控制主要由控制器与被控制对象组成，通过控制偏差e(t)，分别经过比例、积分、微分调节，从而对被控制对象进行控制[6].PID控制器的输入与输出关系：

(8)

式中Kp、Ki、Kd分别是比例、积分、微分.本文中主要用的是PI控制，输入输出关系为：

(9)

PI控制器的两个参数在控制被对象时分别有不同的作用，它们的取值不同会影响到系统的响应速度、控制精度等.

(1)Kp：Kp的作用主要是调节系统的响应速度，并对系统的调节精度产生影响.当取较大值时，响应的速度会较快，调节的精度也较高.反之会降低响应速度，对调节精度也不利.但Kp不能取过大，会产生超调量，使系统不稳定.

(2)Ki：Ki主要是调节系统的静态误差.当取大值时，可以很快消除系统静态误差.反之，不利于消除系统静态误差从而影响调节精度.Ki的取值也不能过大，过大会产生积分饱和，引起超调.

根据光伏电池的数学模型，模型参数与上述相同采用PI控制对光伏系统分别在T=25 ℃光照强度从1000 W/m2降到600 W/m2时以及光照强度为1000 W/m2温度从25 ℃升到50 ℃时，两种情况下进行最大功率跟踪控制，仿真时间0.2 s.仿真模型如图6所示.

图6 PI控制最大功率跟踪仿真模型

PWM模块的输出由PI控制的输出与三角波比较而得.PWM子系统如图7所示.

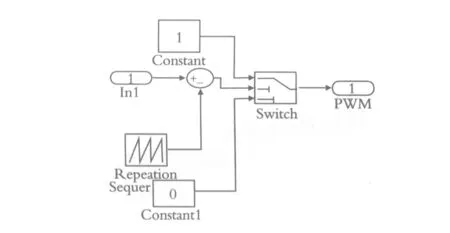
图7 PWM子系统模块图

2.2 扰动法控制

扰动法控制主要是通过对光伏系统输出的电压进行扰动，再观察输出功率的变化，进而决定下一步的控制信号[7]，以达到最大功率点的输出.本文采用改进的扰动法功率控制，首先对电压进行扰动，观察输出功率的变化，若功率增大，则继续原来方向扰动直到输出功率最高点.若加扰动后输出功率减小，则相反方向扰动，寻找最大功率点.扰动法功率控制的流程图如图8所示.

图8 扰动法程序流程图

根据图8所示流程图可在Matlab/simulink中建立扰动法的仿真模型图如图9所示.

图9 扰动法仿真模型图

采用相同的光伏电池数学模型，为了与PI控制形成对比，参数设置与PI控制相同，建立基于扰动法功率控制的仿真模型如图10所示.

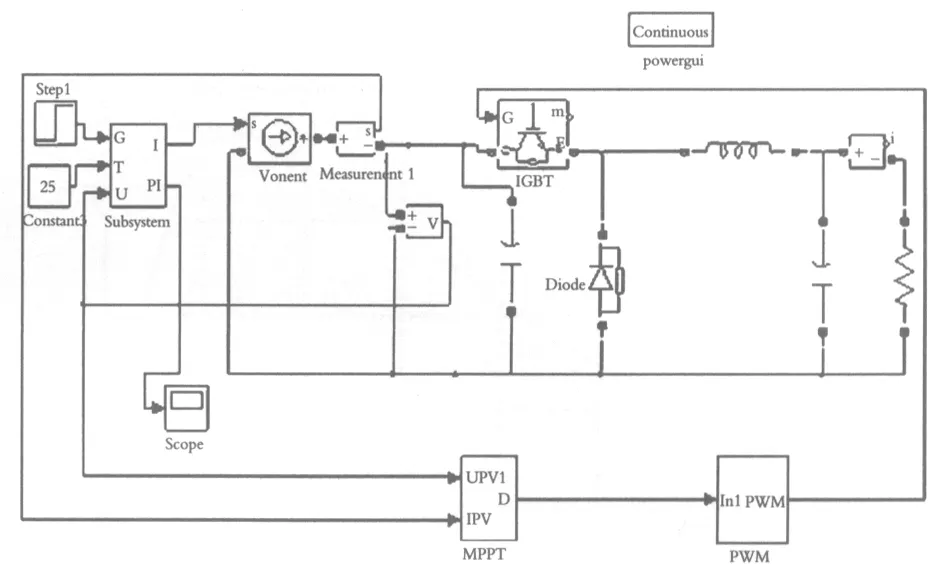
图10 扰动法功率控制仿真模型图

3 仿真结果分析

通过对上述两种控制算法的仿真建模，得到PI控制仿真结果如图11、图12、图13所示.其中，图11是在T=25 ℃，G=1000 W/m2时的光伏电池输出功率.图12是T=25 ℃，光照强度G在仿真0.1 s后从600 W/m2增加到1000 W/m2时的光伏电池输出电压与输出功率波形.图13是G=1000 W/m2时，T从开始25 ℃在0.1 s后提高到50 ℃时的光伏电池输出电压与功率.

图11 T=25 ℃，G=1000 W/m2时的光伏电池输出功率

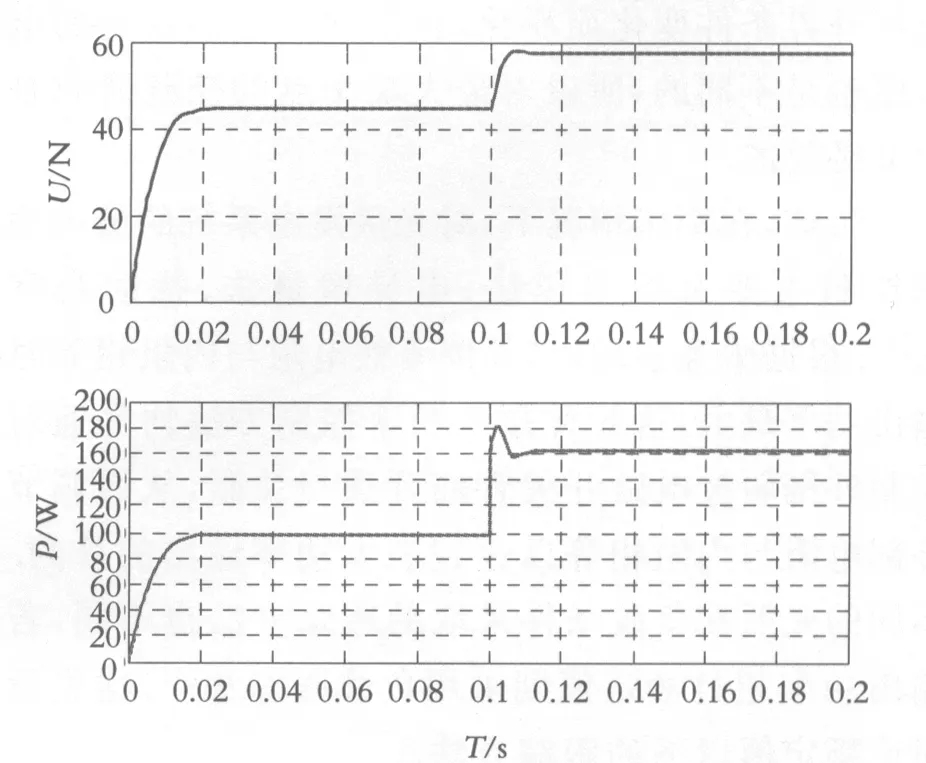
图12 T=25 ℃，G变化时输出电压与功率

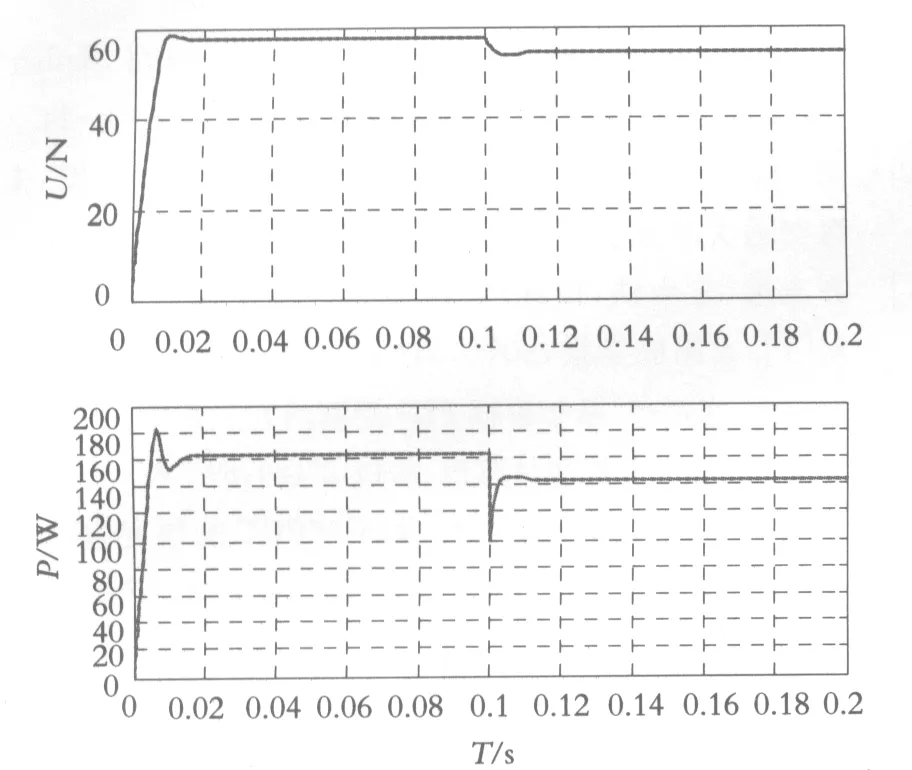
图13 G=1000 W/m2，温度变化时输出电压与功率

扰动法功率控制仿真如图14、图15、图16所示.

图14 T=25 ℃，G=1000 W/m2时的

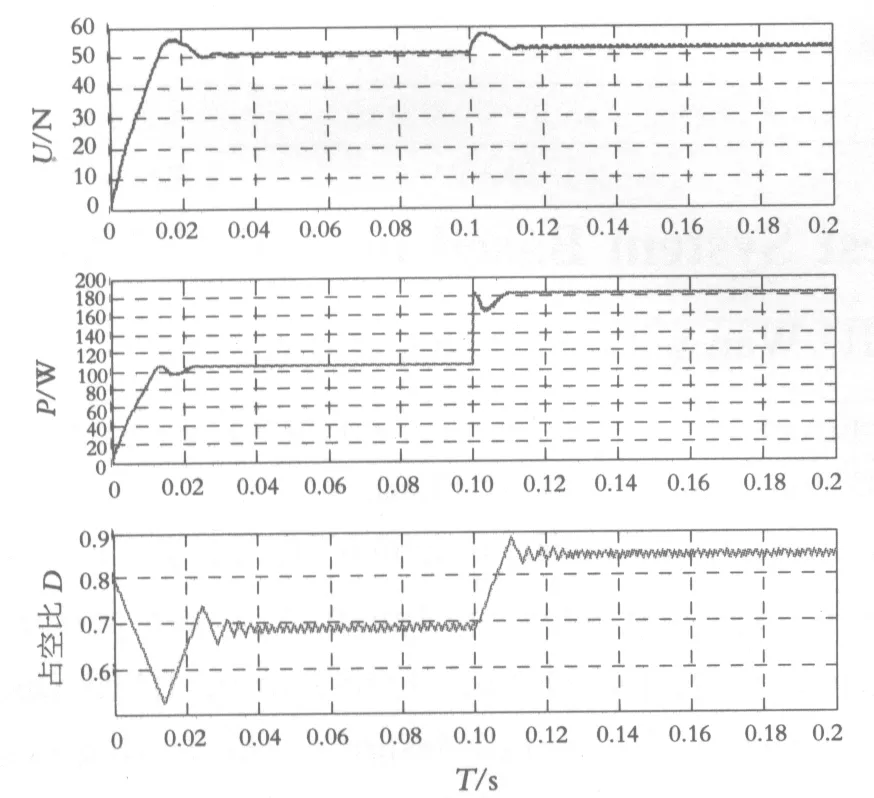
图15 T=25 ℃，光照强度变化时光伏系统输出曲线

图16 G=1000 W/m2温度变化时，光伏系统输出曲线

图14是在T=25 ℃，G=1000 W/m2时的光伏电池输出功率与占空比.图15是T=25 ℃，光照强度G在仿真0.1 s后从600 W/m2增加到1000 W/m2时的光伏电池输出电压与输出功率以及占空比波形.图16是G=1000 W/m2时，T从开始25 ℃在0.1 s后提高到50 ℃时的光伏电池输出电压与功率和占空比波形.

由以上两种方法的仿真结果可知，传统PI控制输出结果稳定，波动小，能很快的跟踪到输出功率点并稳定运行，在稳定运行时基本没有振荡，但输出效率不高，很难跟踪到最大功率点运行.扰动法输出效率高，响应速度快，可以在最大功率点附近运行，但是有波动，只能在最大功率点附近波动运行.

4 结 论

本文建立了光伏电池数学模型，在额定功率以下时，采用了两种不同的控制方法在该模型的基础上对光伏发电系统进行功率控制仿真.仿真了在温度和光照强度变化时的几种情形，通过对DC-DC的控制，验证两种控方法功率跟踪情况，并分析了传统PI控制算法与改进扰动法的各自优缺点.鉴于这两种方法的特点，可以看出具有互补性质，把两种控制方法结合起来对功率跟踪控制可以进一步进行研究.本文的仿真对光伏发电系统功率控制问题有一定的启发作用，通过对本文的分析，可以得出更好的控制算法，从而提高发电效率.同时，本文的方法还可以推广到其它形式的发电系统中，如风光互补发电系统等.

[1] Yun Wei Li，Ching-Nan Kao.An Accurate Power Control Strategy for Power Electronics Interfaced Distributed Generation Units Operating in a Low-Voltage Multibus Microgrid[J].IEEE TRANSACTIONS ON POWER ELECTRONICS,2009,24(12):2977-2988.

[2] Aissa Chouder，Santiago Silvestre，Nawel Sadaoui，Lazhar Rahmani.Modeling and Simulation of a Grid Connected PV System Based on the Evaluation of Main PV Module Para-meters[J]. Simulation Modelling Practice and Theory，2012，20:46-58.

[3] 侯金明，许 鹏.基于四参数模型的光伏阵列Matlab/Simulink仿真模型[J].可再生能源，2013，31(6)：10-14.

[4] 艾 芊，郑志语.分布式发电与智能电网[M].上海：上海交通大学出版社，2012：65-74.

[5] 齐志远，王生铁，田桂珍.风光互补发电系统的协调控制[J].太阳能学报，2010，31(5)：654-660.

[6] 孙然然，张寅孩.基于模糊PID 控制的光伏系统最大功率点跟踪[J].工业控制计算机，2014，27(5)：69-71.

[7] 王厦楠.独立光伏发电系统及其MPPT的研究[D].江苏：南京航空航天大学硕士学位论文，2008.

Research on Power Control of Photovoltaic Power Generation System Under the Rated Power

DING Lu,DENG Qiu-ling, CHENG Ke, XIE Ji-tang

(College of Elect. and Information，Hunan Institute of Engineering， Xiangtan 411101， China)

Through the analysis of the photovoltaic cells,and the application of Matlab/simlink simlation software tools,the mathematical model and simulation model of photovoltaic cells are established.Based on this mode,and aiming at the problem of low efficiency of photovoltaic power generation system, the maximum power point tracking problem is studied in the rated condition photovoltaic. The two methods of the maximum power point tracking control of the PID and improved perturbation control are stimulated, The advantages and disadvantages of the two methods are analyzed respectively. The results of simulation show that，the oscillation of PID control is small, and the improved perturbation method is more efficient.

photovoltaic power generation；maximum power point tracking；PID control；improved perturbation control

2014-12-08

湖南省科技计划项目(2012GK2079);湖南省高校科技创新平台建设项目(12K126).

丁 陆(1990-)，男，硕士研究生，研究方向：分布式风光互补发电技术.

TP391.9

A

1671-119X(2015)02-0009-06