电气距离计算在风电故障分析中的应用

王卓越，曾令全，陈树勇

(1.东北电力大学 研究生部，吉林 吉林 132012;2.中国电力科学研究院，北京 100196)

1 直流侧电压波动分析

1.1 稳定图定阶原理

近年来风电连锁事故频发，而是否引起连锁故障与节点间电气距离的大小有着密切的联系。电气距离的概念，本质上来讲是表征系统中两个节点间的电气关系的物理量，是一种能量的传递，所以需要得到一个恰当的指标，清晰地反应能量传递的距离和大小等。关于电气距离的计算方法有多种［1－3］，多数情况下采用阻抗法。但该方法在功率变化较大的情况下，难以保证计算结果准确度。基于此，本文提出采用灵敏度法计算电气距离，以弥补阻抗法的不足。

1 电气距离的计算方法

文献［4－17］提出了多种不同的电气距离计算方法。但主要可以分为三类:灵敏度法、阻抗法、相角法。

1.1 灵敏度法

对于线性时不变系统，为了衡量系统元件对网络参数的影响，定义灵敏度的概念。灵敏度法现在多用于对电网的分区，常用的灵敏度计算方法有:电压幅值随无功功率变化的灵敏度;电压相角随有功功率变化的灵敏度灵敏度越大，表明两节点间电气距离越小，节点耦合关系就越强。利用PQ分解法求取潮流的无功迭代方程是

将式(1)进行求逆运算可得到:

如果节点j之外的系统其他的节点都没有无功功率发生变化，则节点i和j之间的电气距离可以定义为

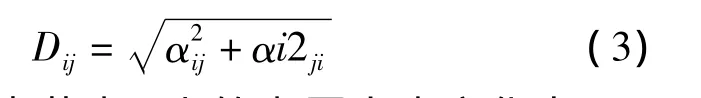
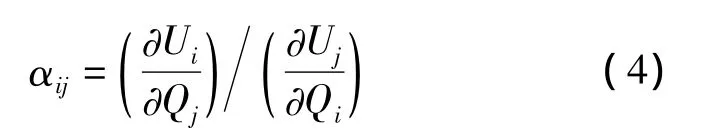
多数情况下，αij≠αji，故可以保证矩阵 Dij的稳定性，又可以保证电气距离的对称性。然而，灵敏度法在物理意义上有着先天的缺陷，不论还是都是没有量纲的，其本质只能反映变化的程度和快慢，偏导数的原函数也不存在物理意义。采用∂U计∂Q算电气距离时，前提是默认两点间的功率传输是绝对封闭的，而文献［18］已经证明，严格来说系统中所有节点间都有功率耦合关系，所以灵敏度法的精确度还有待验证。

1.2 阻抗法［19］

所谓阻抗，由欧姆定律可知，阻抗等于电压与电流的比值。关于阻抗法的计算方法，电气距离可以用节点阻抗矩阵中的非对角元素Zij来表示。其电压的物理意义:节点j注入单位电流，其他节点都不注入电流时，节点i的电压。如图1所示。

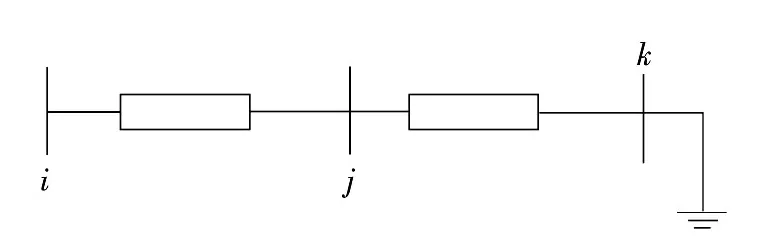
图1 阻抗法的物理意义Fig.1 Physical significance of impedance method

这种方法作者认为不能全面地反映电气距离。理由如下:

1)线路阻抗的大小并不能真实反映功率的传输，如图2所示。

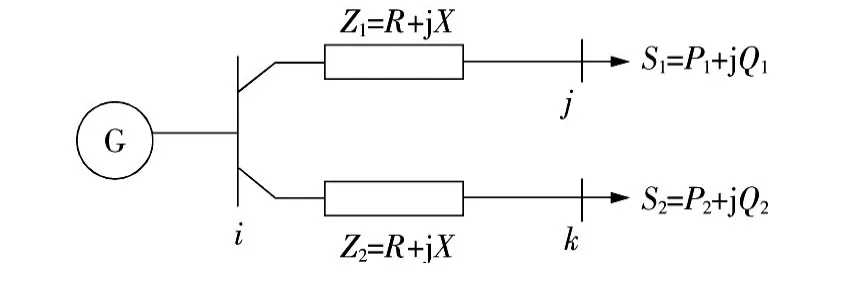
图2 功率传输示意图Fig.2 Schematic diagram of power transmission

2)假设图中Z1=Z1，然而当负荷S1=2S2时，节点ij之间的传输功率就将是ik之间的2倍。

1.3 相角法

文献［20］中提到用相角θ来表征两节点间的电气距离。

式中:l为输电线路的几何距离;f为系统的频率;v为该线路上电磁波传递的速度;t为功率传播所需要的时间;θ为输电线路传输所引起的相角偏差。

对于π型等值电路将线路输送端和受端看作一个等效的二端网络，如图3所示。

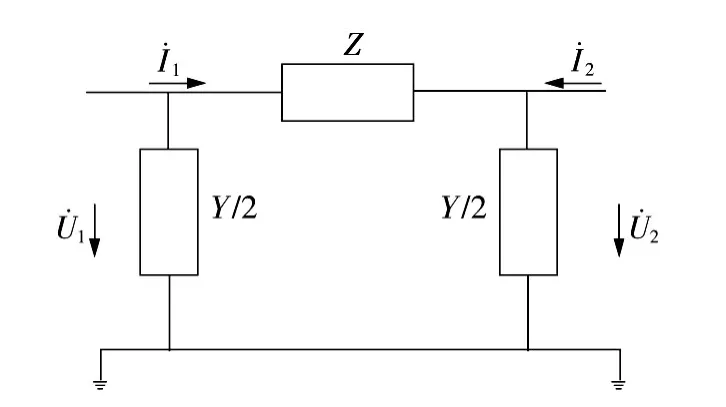
图3 π型等值电路Fig.3 π type equivalent circuit

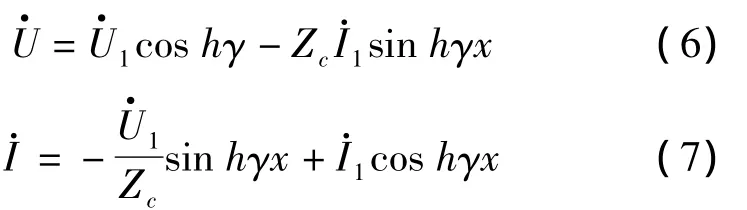
为了简化公式，令

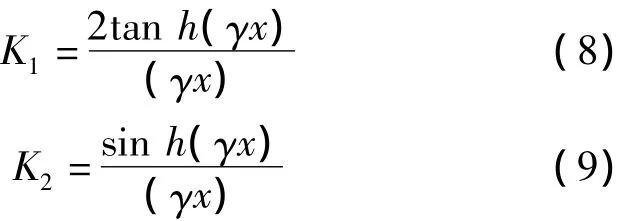
则Z和Y由下式表示:

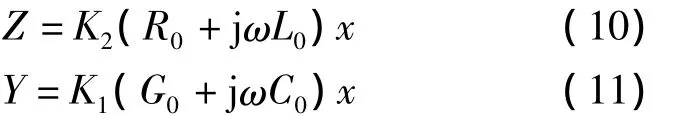
从式(10)和式(11)可以看出，当x距离很小时，且K1≈K2≈1，此时可以求出集中参数的模型。求出的电压相角是忽略了由于电气距离而引起的角度。

2 电气距离计算法的选择与比较

灵敏度法描述的电气距离表示的是电压和无功两个不同单位变量之间的关系，只能反映单一节点注入无功功率发生变化时节点电压变化之间的关系。灵敏度法计算是将整个系统线性化，因此只适用于小干扰。以CEPRI－36节点系统分析对比两种电气距离的计算方法，其系统接线如图4所示［21］。

选取节点50为参考节点，计算节点50到各个网络节点的电气距离 Z50j，in、D50，j(j=1，2，3，…，36)，然后再由PSASP暂态计算得到对应母线短路时BUS50的暂态最低电压。结果如表1所示。

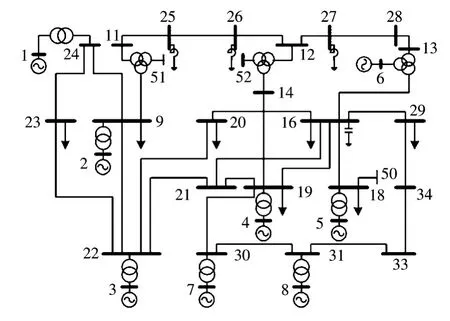
图4 系统接线图Fig.4 System wiring diagram

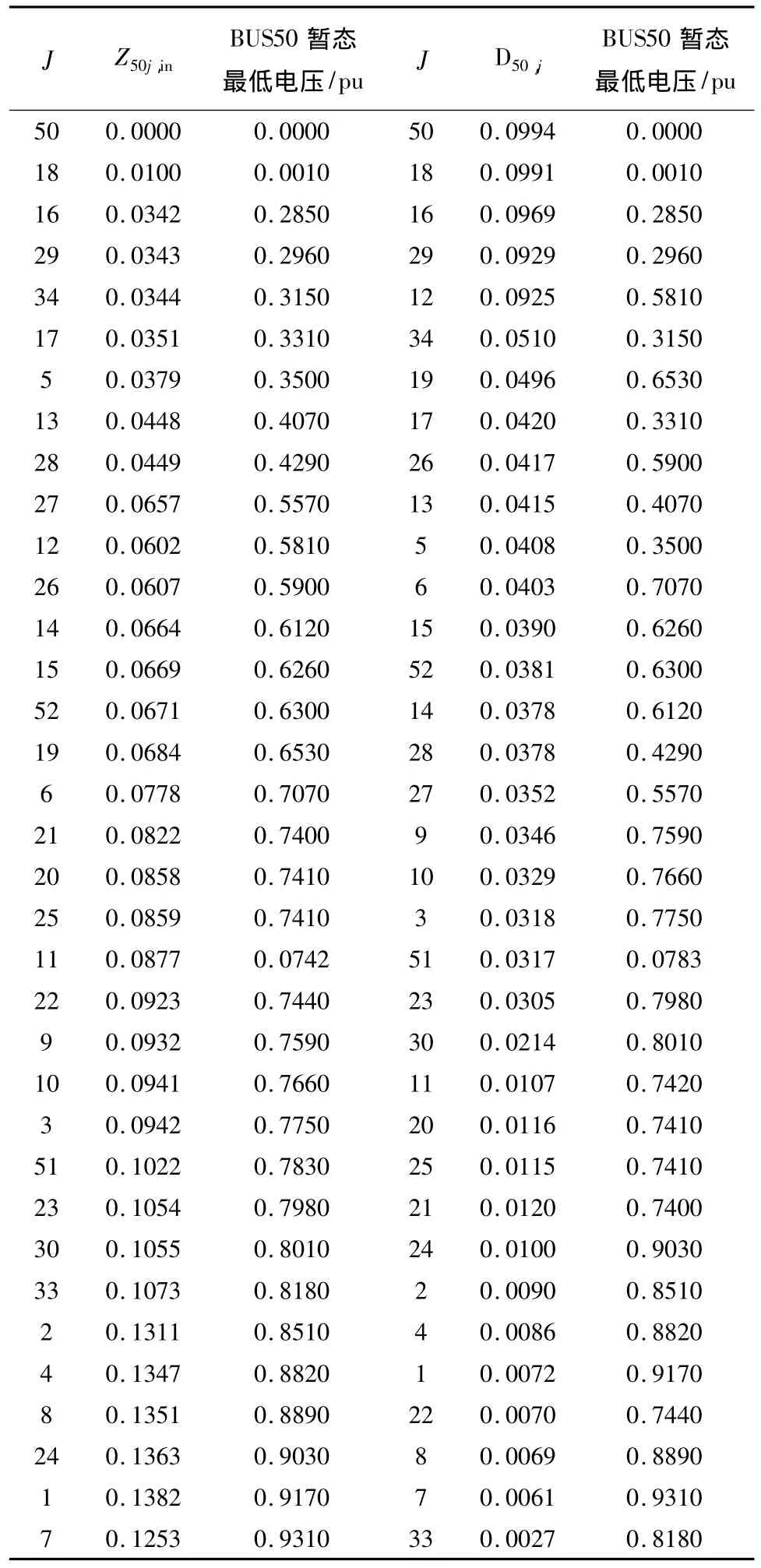
表1 BUS50的暂态最低电压Tab.1 BUS50 transient lowest voltage

通过比较可以发现，当采用阻抗法电气距离计算时，母线最低电压的大小是与电气距离的大小成线性关系的。而当采用灵敏度法时，母线最低电压与电气距离之间并没有直接的联系，这是因为在用灵敏度法进行计算时，

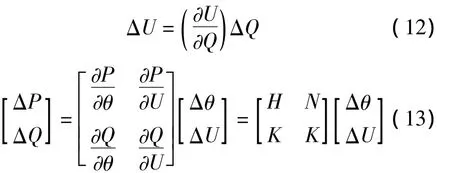
设节点50为PQ节点，假设其有功的变化量ΔP=0，则有

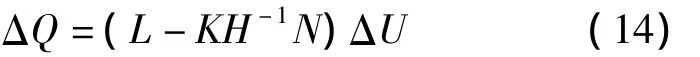
矩阵中表现出了PQ节点无功变化对电压大小的灵敏度，但PU节点和平衡节点的灵敏度却没有能够求出来。这是由于在写方程初始条件时，将PU节点和平衡节点的电压幅值都假设为不发生变化。而真实情况中，当这些节点的无功发生变化时，即便电压不变，PQ节点的电压也会因此随之发生变化。显然，在同时研究多节点特性时，灵敏度法显然有其天生的劣势。

3 电气距离灵敏度法在风电中应用

3.1 相邻风场连锁故障的可能性分析

多个风电场相邻时，若某一风电场近端发生严重故障，将其撬棒投入，可使风机进入普通异步机运行模式。而且该风场在实现低电压穿越时，会对相邻风电场造成影响，甚至会造成相邻风电场撬棒连锁动作。而衡量是否连锁故障的指标，在于相邻风场对撬棒动作风场的无功灵敏度，即灵敏度电气距离的大小。将表1按照节点顺序重排如表2所示。

从表2中数据可以看出，连接阻抗小的节点无功灵敏度未必大，因此，在判断是否发生连锁故障，以及选用相应的保护方案，应采用灵敏度法计算电气距离，会更加精确。

3.2 含风电的电压分区

电网分区的原则是，将电网按照电气联系的紧密程度进行合并和解耦，制定分区控制策略的，从而更加有效地对电网潮流进行控制。

电压分区通常着眼于电压/无功灵敏度，利用灵敏度的雅各比矩阵进行计算求解，再根据最优化方法，如遗传算法、Tabu搜索法、模拟退火法等。

对含风电的电网进行分区关键在于如何恰当地处理异步发电机的模型。对于普通的异步发电机，一般将其视为PQ节点，如图5所示。

表2 电气距离排序Tab.2 Electrical distance sorting

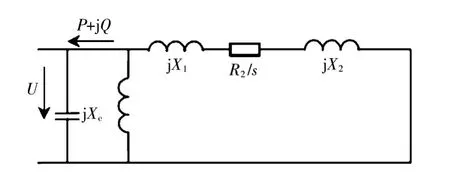
图5 异步发电机等值电路图Fig.5 Asynchronous generator equivalent circuit

机端电压和无功功率的表达式为

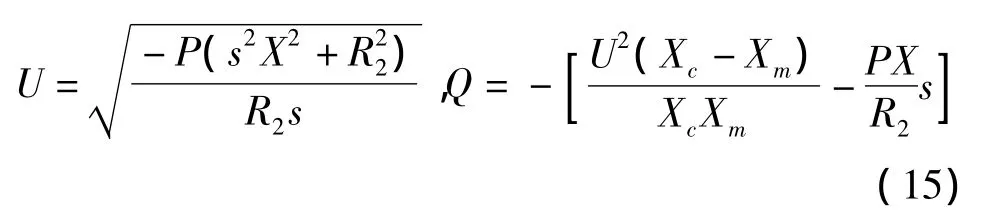
由于风电机组的输出有功与风速密切相关，可以先考虑其有功P为恒定，其无功与转差率和机端电压相关。若忽略转差率的影响，可以得到无功对电压的关系式

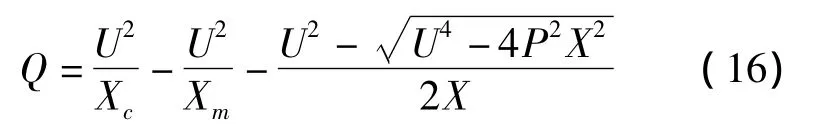
式中:R2为转子电阻值:Xc为补偿电容电抗;Xm为激磁电抗。

对于双馈机组，由于其端电压基本稳定，可以直接看作PQ节点。

4 结论

本文分析了三种不同的电气距离计算方法，且重点比较了常用的阻抗法和灵敏度法的电气距离计算方法。

1)阻抗法由于计算简便，排序简单，具备明确的物理量纲，因此用阻抗法进行暂态电压的计算时，可以和各个节点形成线性关系。适合运用在故障预警和排序等大的控制领域。

2)灵敏度法无量纲，排序困难，然而其针对性强，可以直接定位出无功与控制节点电压的耦合度，对电压分区和关键节点控制的效果较好。

［1］ 熊虎岗，程浩忠，孔涛.基于免疫－中心点聚类算法的无功电压控制分区［J］.电力系统及其自动化，2007，31(2):22－26.XIONG Hugang，CHENG Haozhong，KONG Tao.Network portioning for reactive power/voltage control based on immune－central point clustering algorithm［J］.Automation of Electric Power Systems，2007，31(2):22 －26.

［2］ 杨秀媛，董征，唐宝，等.基于模糊聚类分析的无功电压控制分区［J］.中国电机工程学报，2006，26(22):7－9.YANG Xiuyuan，DONG Zheng，TANG Bao，et al.Power network portioning based on fuzzy clustering analysis［J］.Proceedings of the CSEE，2006，26(22):7－9.

［3］ COTILLA－SANCHEZ，E.Multi－attribute partitioning of power networks based on electrical distance［J］.Power Systems，IEEE Transactions on，2013，28(4):4979－4987.

［4］ 郝文波，于继来.基于负荷受电路径电气剖分信息的配电网重构算法［J］.中国电机工程学报，2008，28(19):42－48.HAO Wenbo，YU Jilai.Distribution network reconfiguration algorithm based electrical dissection information of load path［J］.Proceedings of the CSEE，2008，28(19):42－48.

［5］ 王海霞，李卫东.考虑节点间电气距离的潮流追踪损耗分摊方法［J］.电网技术，2008，32(2):42－48.WANG Haixia，LI Weidong.Power flow tracking of loss allocation considering electric distance between nodes［J］.Power System Engineering，2008，32(2):42－48.

［6］ HONG LIU.Notice of Retraction A new method about calculating electrical distance［C］.Power Engineering and Automation Conference(PEAM).IEEE，2011:282 －285.

［7］ YANSONG WANG.Study on structural vulnerabilities of power grids based on the electrical distance［C］.Innovative Smart Grid Technologies－Asia(ISGT Asia).IEEE，2012:1－5.

［8］ LIU HONG，BAOHAI，LIU LEI.Caculationg Electrical Distance［A］.IEEE Power Engineering and Automation Conference.Wuhan，China:IEEE，2011.

［9］ 赵峰，孙宏斌，张伯明.基于电气分区的输电断面及其自动发现［J］.电力系统自动化，2011，35(5):42－47.ZHAO Feng，SUN Hongbin，ZHANG Boming.Electrical zone division based automatic discovery of flowgates［J］.Automation of Electric Power Systems，2011，35(5):42 －47.

［10］ 周海强，鞠平.基于机电距离的聚类方法在动态等值中的应用［J］.电力系统自动化，2008，32(3):42－47.ZHOU Haiqiang，JU Ping.Application of clustering method based on electromechanical distance between different units in power system dynamic equivalence［J］.Automation of Electric Power Systems，2008，32(3):42 －47.

［11］ LAGONOTTE P，SABONNADIERE J C，LEOST J Y，et al.Structural analysis of the eletrical system:application to secondary voltage control in France［J］.IEEE Transactions on Power Systems，1989，PWRS－4(2):479－486.

［12］ HANG LIU，ARYAN BOSE.A fast voltage security assessment method using adaptive bounding［J］.IEEE Transactions on Power Systems，2000，15(3):1137－1141.

［13］ S.BLUMSACK，P.Hines，Patel.Defining power network zones from measures of electrical distance［J］.IEEE Transactions on Power Systems，2005，12(1):52－60.

［14］ 谭玉东，李欣然，蔡晔，等.基于电气距离的复杂电网关键节点识别［J］.中国电机工程学报，2014，34(1):146－151.TAN Yudong，LI Xinran，CAI Ye，et al.Critical node identification for complex power grid based on electrical distance［J］.Proceedings of the CSEE，2014，34(1):146－151.

［15］ HUANG KAI.Research on partition for automatic voltage/var control based on electrical distance to generator［C］.Innovative Smart Grid Technologies－Asia(ISGT Asia)，2012 IEEEInnovative Smart Grid Technologies－Asia(ISGT Asia)，2012 IEEE.IEEE，2012:1－4.

［16］ 张怡，吴文传，张伯明，等.电磁－机电暂态混合仿真中机电测故障的仿真方法［J］.中国电机工程学报，2012，32(19):81－89.ZHANG Yi，WU Wenchuan，ZHANG Boming，et al.Simulation method of faults on electromechanical side in electromagnetic and electromechanical hybrid simulation［J］.Proceedings of the CSEE，2012，32(19):81－89.

［17］ 刘宏.一种基于相角描述的电气距离计算方法［D］.北京:华北电力大学，2007.LIU Hong.A new method about calculating electrical distance based on phase［D］.Beijing:North China Electric Power University，2007.

［18］ RUSEK，S.The problems of electrical distance in connection with the operation of wind power generator［C］.Environment and Electrical Engineering(EEEIC)，2010 9th International Conference on.IEEE，2010:65－68.

［19］ 杨雄平.电力系统网络拓扑结构分析及运行方式组合研究［D］.武汉:华中科技大学，2007.YANG Xiongping.Research on power system network topology analysis and the combination of operation modes［D］.Wuhan:Huazhong University of Science and Technology，2007.

［20］ 盛戈埠.电力系统二级电压控制的新理论与新方法研究［D］.武汉:华中科技大学，2003.SHENG Gebu.Research on the novel theory and method of power system secondary voltage control［D］.Wuhan:Huazhong University of Science and Technology，2003.

［21］ CEPRI－36v6算例说明［S］.中国电力科学研究院，2007.