变压器杂散损耗的三维有限元分析

陈起超，刘文里，李 航，陈 聪

(1.哈尔滨理工大学 电气与电子工程学院，哈尔滨 150080;2.黑龙江省电力科学研究院，哈尔滨 150030)

大容量电力变压器正常运行时，其杂散损耗可以达到负载损耗的30% ～40%，所以杂散损耗不可忽视［1］。由于变压器漏磁场分布的不规律性及结构件的不规则性，在变压器厂进行工程计算时，通常不能单独具体地给出各个金属结构件的损耗值，而是作为附加损耗的一部分进行估算。因此本文通过采用ANSYS有限元软件对大型变压器金属结构件三维漏磁场及涡流损耗进行分析，进而得到各金属结构件的漏磁场和涡流损耗的具体分布及数值大小，以利于为大型变压器的设计提供参考依据。

1 模型简化处理及建模计算

1.1 模型简化处理

以一台SFZ10－120000/220三相五柱式电力变压器为例进行计算。为便于计算以及更好地划分网格，提高计算准确性，现对其做出如下简化及假设:

1)变压器整体结构前后对称;

2)变压器的油箱壁及其他铁磁材料近似认为线性、均匀且各向同性;

3)各相绕组安匝数之和为零，电流在绕组内分布均匀;

4)在求解场域中，场量的变化方式为随时间进行正弦变化，忽略其中的高次谐波;

5)忽略其中位移电流产生的影响;

6)油箱的箱盖、箱壁与箱底连接方式均为直角连接。

1.2 建模计算

1.2.1 金属结构件涡流损耗计算

首先进行漏磁场计算，然后通过漏磁场计算求得的矢量磁位→A标量点位φ计算得出涡流密度Je的分布，进而通过涡流密度求得单位体积内的涡流损耗密度We为

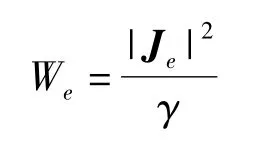
金属结构件表面产生的涡流损耗Ws为

金属结构件产生的涡流损耗W为

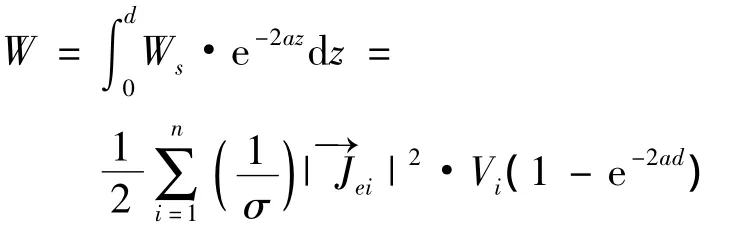
式中:n是积分点的个数;Wei是积分单元i内涡流损耗的密度;Jei是积分单元i内电流密度;σ是材料电导率;Vi是积分单元i的体积;d是材料厚度;α是电磁波的衰减系数，与透入深度成倒数［2］。

1.2.2 确定单元类型及材料属性

材料属性均按变压器的实际参数进行定义，如表1所示。单元类型为solid117，绕组、铁心、变压器油、空气的自由度为 AZ，其余为 AZ和VOLT。

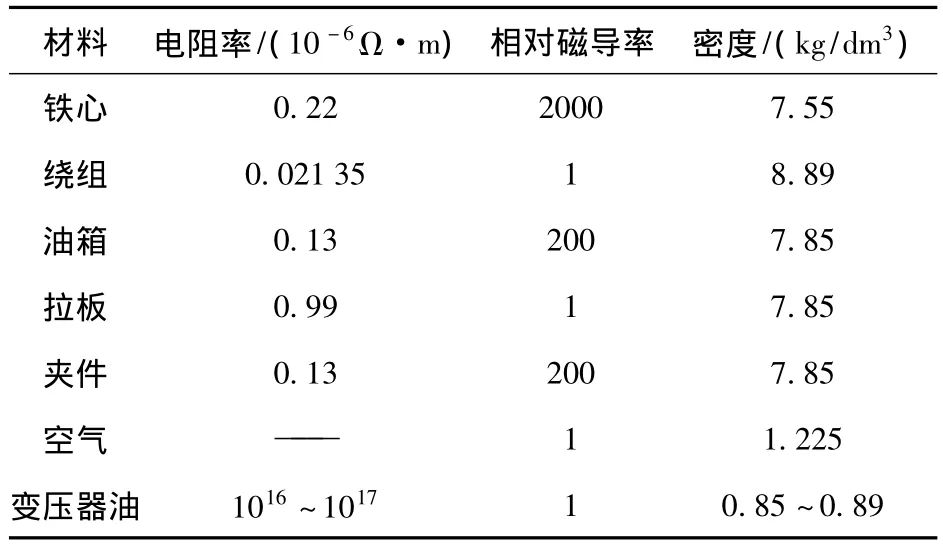
表1 变压器材料属性表Tab.1 Transformer material attribute table

1.2.3 建模

在建模时将变压器的主要部件全部包括在内，能够更加真实地反映变压器实际漏磁场的分布情况，模型如图1、图2所示。

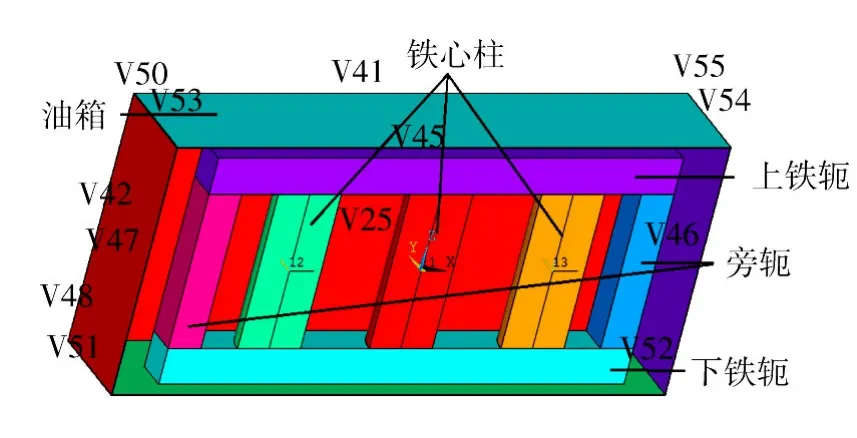
图1 变压器油箱、铁芯及旁轭漏磁场计算模型Fig.1 Tank，iron core and a side yoke of transformer leakage magnetic field calculation model

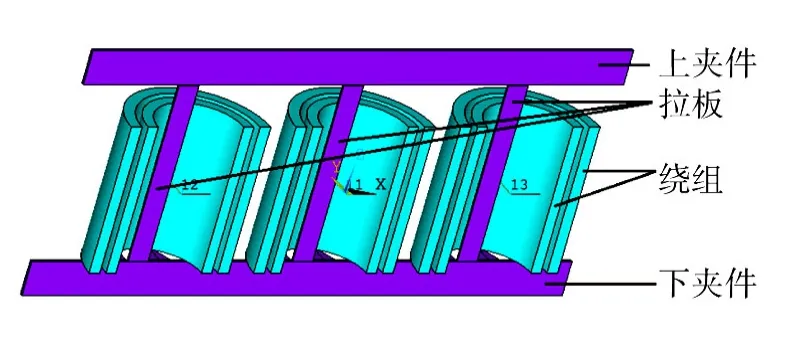
图2 变压器绕组及结构件漏磁场计算模型Fig.2 Windings and structure parts of transformer leakage magnetic field calculation model

1.2.4 剖分

变压器油箱壁较厚，且属于铁磁材料，当其处于正弦交变漏磁场中，由于集肤效应的影响，需要考虑其透入深度问题。箱体的透入深度计算表达式为

式中:ω为正弦变化的角频率，在工频情况下ω=2πf=314;电导率γ=7.6923×106s/m;材料磁导率μ =μ0μr=4π ×10－7×200=2.512 ×10－4H/m。

因此可得变压器油箱的透入深度d=1.8 mm，小于其厚度。所以在对变压器绕组、拉板、夹件以及油箱进行扫略剖分时，在沿油箱壁厚度方向上要进行多层剖分，然后再对变压器油区及铁芯铁轭部分采用自由剖分，并尽量保证变压器整体各个区域的剖分网格的大小近似相等，提高模型的计算精度。

1.2.5 确定边界条件及激励

采用棱边单元法计算变压器漏磁场及涡流损耗，需要对油箱外侧及对称面施加平行边界条件，其余均默认为垂直边界条件。电流密度按磁势平衡条件施加在绕组上作为激励。

2 变压器油箱、拉板及夹件漏磁场与涡流损耗分析

2.1 变压器油箱漏磁场与涡流损耗分析

按计算步骤计算后，可得到油箱、拉板及夹件漏磁场分布云图。油箱漏磁场分布云图如图3所示。

以油箱壁整体来看，绕组外径与油箱壁中部最接近的地方漏磁密度较大。其中以中间铁心柱绕组外径与油箱壁最接近的地方漏磁密度最大，这是由于两侧铁心柱上绕组产生的漏磁场相互叠加并作用于油箱壁最中间区域，使这一区域闭合的磁力线最多，漏磁密度最大。

油箱壁内表面沿幅向中轴线漏磁分布图如图4所示。

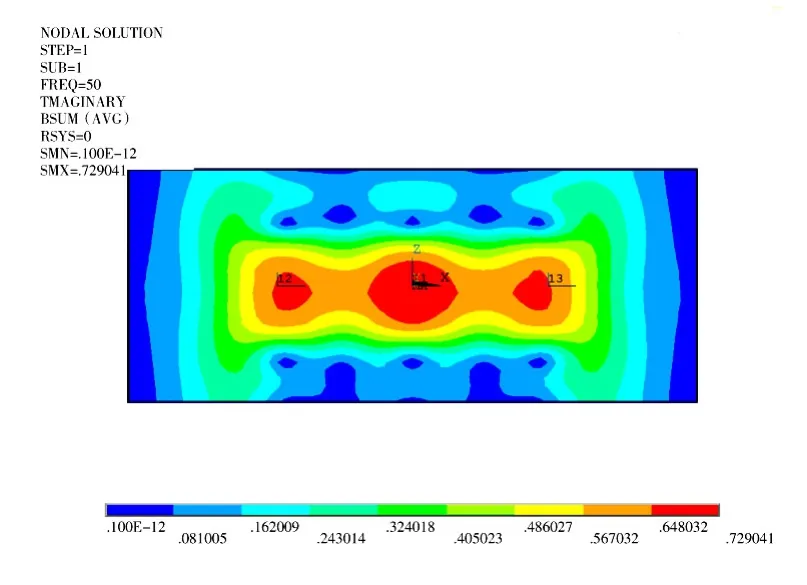
图3 变压器油箱漏磁场分布Fig.3 Transformer tank leakage flux distribution

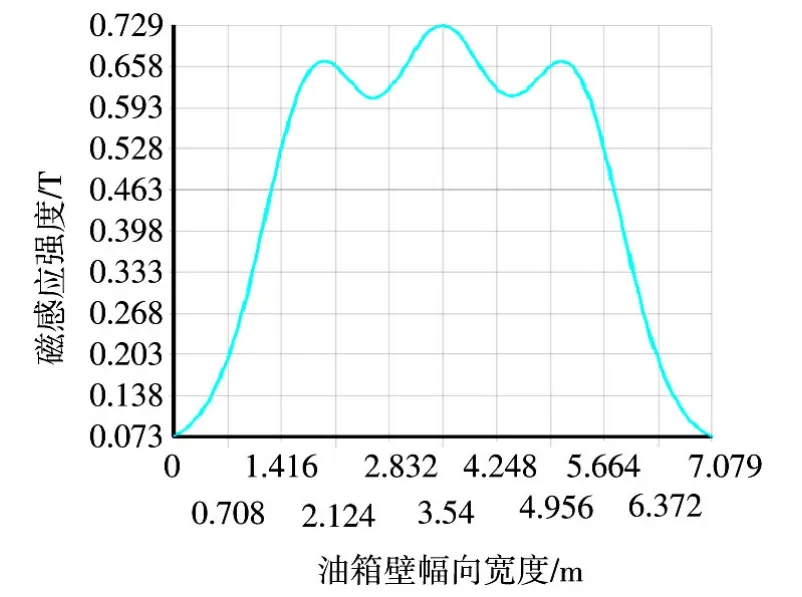
图4 油箱壁内表面沿幅向中轴线漏磁分布图Fig.4 Leakage magnetic field distribution diagram of tank wall inner surface along the radial axis

通过图4的曲线可以更加明显看到，中间铁芯柱上的绕组所对应的区域最大漏磁密度要明显高于另两侧铁芯柱上绕组所对应的区域。综合图3、图4可以看出，漏磁密度沿轴向方向都是远离绕组外径的地方漏磁密度变小，反之则变大。

油箱壁内表面轴向中轴线漏磁分布如图5所示。由于3个铁芯柱上绕组对应区域的漏磁密度在沿轴向方向的变化趋势基本相同，这里只单独对中间铁芯柱上绕组所对应区域进行分析。

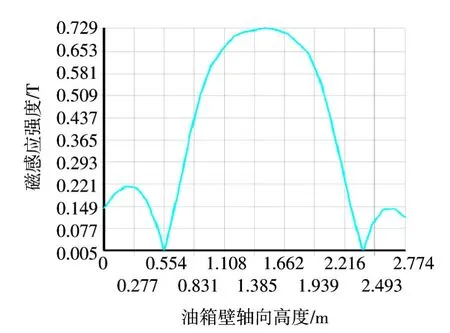
图5 油箱壁内表面轴向中轴线漏磁分布Fig.5 Leakage magnetic distribution of tank wall inner surface in the axial direction

综合图4、图5的曲线可以清楚看到漏磁密度沿高度和宽度方向的变化关系，油箱壁左右两侧及上下边缘区域的漏磁密度变化幅度较大，这是由于其距离绕组较远，能够通过的磁力线大量减少，漏磁密度快速下降。

油箱壁的内表面沿切向的漏磁分布如图6所示，油箱壁的内表面沿法向的漏磁分布如图7所示。

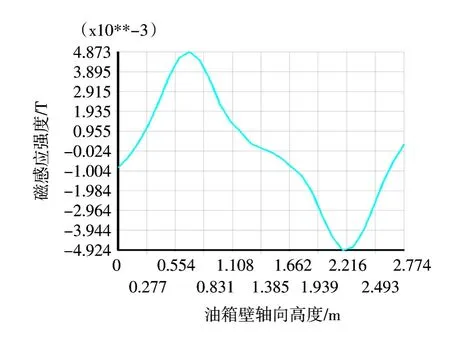
图6 油箱壁的内表面沿切向的漏磁分布Fig.6 Leakage magnetic field distribution of tank wall inner surface along tangential direction

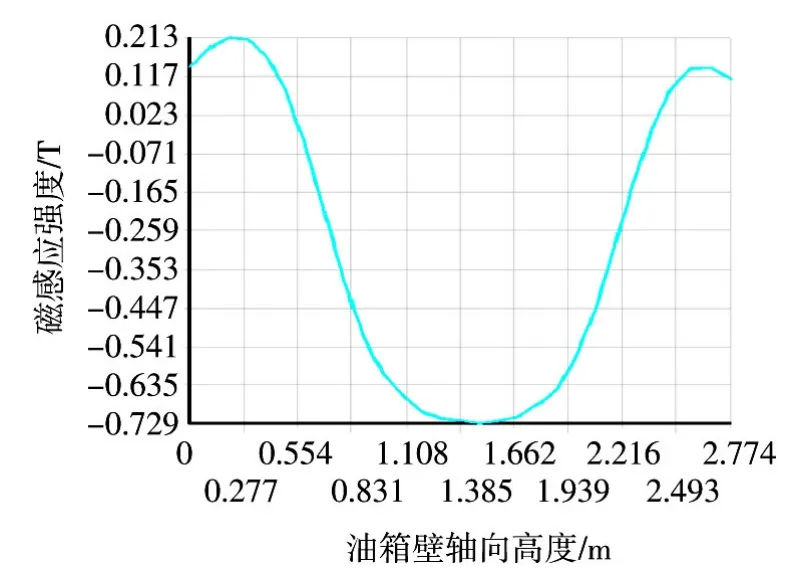
图7 油箱壁的内表面沿法向的漏磁分布Fig.7 Leakage magnetic field distribution of tank wall inner surface along normal direction

通过图6可以看出，与绕组端部对应的区域内不仅油箱轴向漏磁密度变化明显而且磁力线的方向发生改变。改变的原因根据电磁波的折射原理可知，当磁力线的入射角达到一定度数时，在油箱壁内磁力线的方向发生改变［3］。将图6和图7一起分析可以看出，漏磁密度的最大幅向分量产生在油箱壁与绕组所对应的区域内，漏磁密度的最大轴向分量产生在油箱壁与绕组中部所对应的区域内。产生这种现象的原因是磁力线在流经绕组到达端部时发生了弯曲，倾斜或垂直进入油箱壁产生了幅向分量的漏磁，然后在经过油箱壁后闭合。油箱壁中部离绕组越近的区域，闭合的磁力线越多，一部分磁力线未到达绕组的端部就直接同油箱壁形成了闭合回路，所以油箱壁中部与绕组最近的区域磁密最大［4］。

变压器油箱壁涡流损耗分布云图如图8所示。

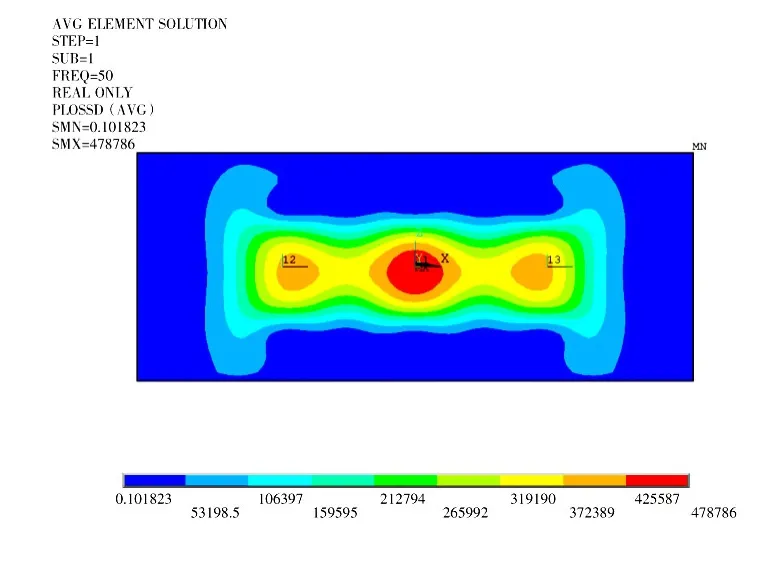
图8 变压器油箱壁涡流损耗分布云图Fig.8 Transformer tank eddy current loss distribution

从图8可以看出，涡流损耗密度的最大处在箱壁中部，涡流损耗的变化规律同其漏磁分布类似，这是由于磁密大的部位感应出的涡流密度也大，涡流密度大的区域涡流损耗密度随之也大，进而损耗也大。

2.2 变压器拉板及夹件漏磁场及涡流损耗分析

拉板漏磁分布云图如图9所示。

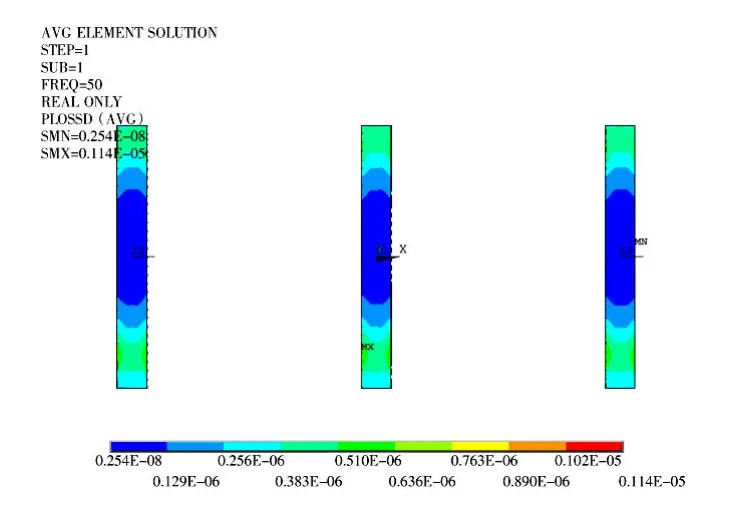
图9 拉板漏磁场分布云图Fig.9 Leakage magnetic field distribution nephogram of pulling plates

从图9可以看出，拉板的漏磁主要集中在与绕组端部附近相对应的区域内，拉板中部的漏磁密度较小，这是因为绕组中部磁力线近似平行于轴向高度，很少发生弯折，无法经过拉板形成闭合回路，而绕组端部磁力线出现弯折，经由对应的拉板区域闭合的磁力线较多。拉板两端被夹件所挡，该位置对应的磁力线大多只能经由夹件闭合，所以该位置漏磁也相对较小［5］。因为此变压器的拉板漏磁密度非常小，所以本文不对其进行涡流损耗分析。

上下夹件的漏磁分布云图如图10所示。

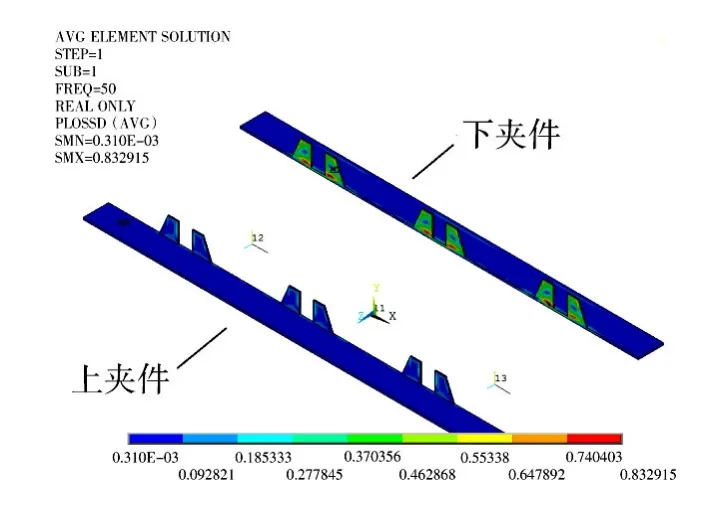
图10 夹件漏磁场分布云图Fig.10 Leakage magnetic field distribution nephogram of clip pieces

从图10可以看出，夹件与主空道位置相对的上下夹件区域漏磁感应强度最大，且下夹件略大于上夹件，而夹件腹板位置上的漏磁感应强度均很小，这是由于主空道上的漏磁感应较大，受铁磁材料的影响，磁力线向外弯折的部分经由夹件闭合，而下夹件离绕组较近，磁力线流入要比上夹件多。

夹件涡流损耗分布云图如图11所示。

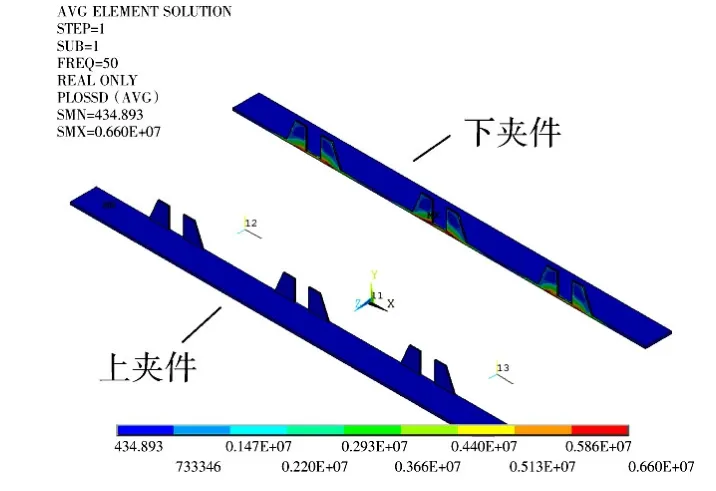
图11 变压器夹件涡流损耗分布云图Fig.11 Clip piece of the transformer eddy current loss distribution

从图11可以看出，涡流损耗密度在靠近铁轭位置最大，其余都很小。夹件的涡流损耗分布与其漏磁场分布近似，同样是因为漏磁密度增大涡流损耗随之增大。

2.3 计算结果

通过ANSYS有限元软件计算求得变压器油箱及夹件的磁通密度、涡流密度及损耗值，由后处理读取计算结果，如表2所示。

表2 计算结果Tab.2 Calculation results

本模型是对称建模，损耗值为全模型的一半，折算到变压器油箱整体的损耗值为34.6 kW，所有夹件的损耗值为6.58 kW。所以变压器的杂散损耗为41.18 kW，工程算法杂散损为 Pzs=0.026×SNZn=43.84 kW，Pzs、SN为额定运行时的容量，Zn为额定运行时的短路阻抗百分数［6］。软件计算所得的值低于工程算法所得的值，这是因为简化建模时忽略掉了一些对整体漏磁场计算影响较小的部件，如螺栓等。

3 结论

1)通过ANSYS软件对一实际变压器进行三维全建模仿真分析，求出其油箱壁、拉板及夹件漏磁密度及涡流损耗的总体分布云图和数值。

2)通过全模型分析，可以看出油箱壁最大漏磁分布受两侧绕组漏磁场影响，而拉板及夹件由于距离绕组非常近，与三组绕组对应的区域漏磁分布基本一致，且与最大漏磁密度基本相同。

3)由软件计算所得损耗值和工程算法所得损耗值近似，证明了软件计算的准确性。

［1］ 路长柏.电力变压器理论与计算［M］.沈阳:辽宁科学技术出版社，2007.LU Changbai.Power transformer theory and calculated［M］.Shenyang:Liaoning Science and Technology Press，2007.

［2］ 阎照文.ANSYS工程电磁分析技术与实例讲解［M］.北京:中国水利水电出版社，2006.YAN Zhaowen.ANSYS electromagnetic analysis technology and engineering examples［M］.Beijing:China Water Conservancy and Hydro－power Press，2006.

［3］ 冯慈璋.工程电磁场导论［M］.北京:高等教育出版社，2000.FENG Cizhang.Introduction to engineering electromagnetic field［M］.Beijing:Higher Education Press，2000.

［4］ 钟燕，刘文里，白永刚，等.自偶变压器绕组漏磁场及涡流损耗的二维数值分析［J］.黑龙江电力，2013，35(6):518－522.ZHONG Yan，LIU Wenli，BAI Yonggang，et al.Two － dimensional numerical analysis of leakage magnetic field and eddy current loss of winding in autotransformer［J］.Heilongjiang Electric Power，2013，35(6):518 －522.

［5］ 刘丹丹，刘文里，王录亮.大型电力变压器拉板涡流损耗的研究［J］.黑龙江电力，2012，34(1):47 －49.LIU Dandan，LIU Wenli，WANG Luliang.Study of eddy current loss of core tie － plate in large transformer［J］.Heilongjiang Electric Power，2012，34(1):47 －49.

［6］ 谢毓城.电力变压器手册［M］.北京:机械工业出版社，2003.XIE Shucheng.Handbook of electric power transformer［M］.Beijing:Machinery Industry Press，2003.