改进先导发展模型在超特高压线路耐雷性能评估中的应用

吴 凡，王艺霖，李 智

(东北电力大学 电气工程学院，吉林 吉林 132012)

随着电力系统输电线路电压等级的不断提高，输电线路杆塔越建越高，加之输电线路走廊地形复杂多变，雷击闪络对输电线路安全运行的影响越来越大［1］。对于超特高压输电线路，绕击是造成雷击跳闸事故的主要原因(因为反击耐雷水平较高)［2］。因此，为使超特高压输电线路安全运行，有必要寻求一种准确的输电线路绕击耐雷性能评估计算模型。目前，超特高压输电线路绕击耐雷性能评估计算模型有电气几何模型(EGM)［3－4］和先导发展模型［5］。EGM和改进EGM在评估超特高压输电线路的高杆塔和大跨越杆塔时存在完全屏蔽的评估结果，与实际运行不符。而先导发展模型阐述了雷电发展过程中上行先导起始、上下行先导发展和最终雷击点选择的全部过程，是相对于电气几何模型更为合理的一种模型。19世纪80年代，Niemeyer提出了关于SF6气体放电的二维介质击穿模型(DBM)［6］，为后人研究自然界雷电放电规律奠定了理论基础。近几年学者在二维和三维的DBM模型基础上，研究了阐述雷电先导发展规律的先导发展模型。然而，由于模型计算的空间分辨率都普遍较低(200 m)，远远大于先导通道热电晕半径(0.5～5 m)和一个梯级长度(约50 m)，这样得到的先导通道图形必然会忽略掉通道中的许多细节特征，并且影响最后击中点的选择;而且在这么低的空间分辨率下，难以对输电线路进行建模和仿真。为此，本文研制了一种能提高放电模拟空间分辨率的改进先导发展模型，并使得最终模拟过程更加接近实际自然放电。

1 雷电通道的分形模拟

1.1DBM模型

先导下行发展若干步后的模拟放电图样如图1所示，中心黑点代表雷电先导通道已发展点，虚线表示下一步发展的可能路径方向。

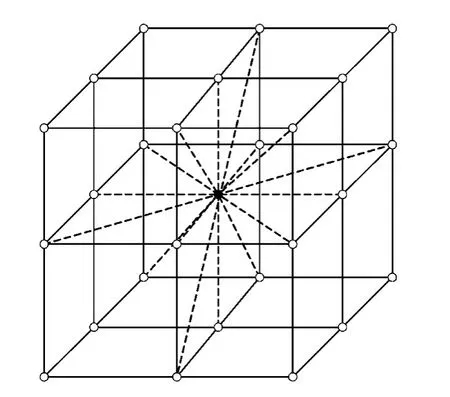
图1 先导下行的可能发展方向Fig.1 Possible direction of development of the leader

在一个计算步长内，计算空间内的电场在准静态近似下，电位满足Paisson方程。将雷云的背景电场和已发展的先导通道电场都作为第一类边界条件，即每一步已发展的格点电位是固定的。每一个可能发展点的电位 φijk可由离散 Laplace方程求取，即

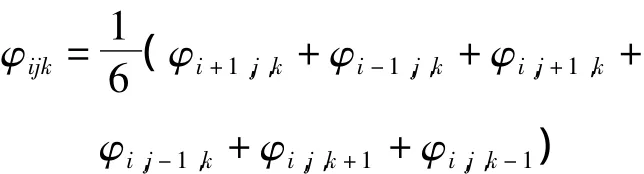
式中:i、j和k分别为x、y和z方向上点的编号。

对每一段虚线来说，其击穿概率表达为它所连接的已发展点(i，j，k)和待发展点(i′，j′，k′)间的电势差的函数。下标 i、j、k 和 i′、j′、k′代表各个点阵的坐标。每一步的放电过程是，若已生成的先导放电通道的放电格点(i，j，k)与邻近的可能发展点(i′，j′，k′)之间的平均场强超过放电临界场强 Ecrit，即

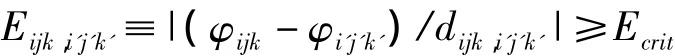
那么，先导即向此方向发展。图1中26个相邻白圈为可能放电点。先导头部向各个方向发展的概率可由下式得出:

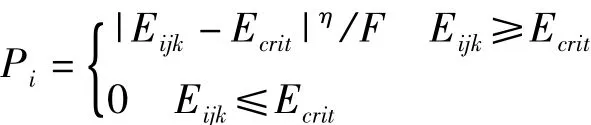
按计算出的概率随机抽取下一步的放电发展方向，假设新的放电通道是由点(i，j，k)向点(i′，j′，k′)击穿，如果沿着放电通道电场强度为 Ech，则(i′，j′，k′)处更新后的电位为

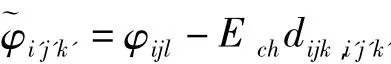
接着开始下一步模拟，如此循环，直到先导通道连接雷云和地面物体，表示雷电击穿。

1.2 计算空间分辨率的提高

本文模型基于三维DBM放电模型，本质是云对地闪电先导的分形模型。但之前的学者为了提高计算速度而降低计算空间的分辨率，这样得到的结果和自然界实际雷电先导通道形状是有偏差的。实际上，雷电下行和上行先导发展过程中，先导通道只有在近地区域会发生明显的分形和曲折，这个区域的放电图样细节会更丰富。因此，为了建立更好的输电线路绕击耐雷性能评估模型，将近地区域的三维计算空间剖分得更细，使此区域的计算分辨率更高。计算空间的横切面网格剖分图如图2所示。利用此种方法，雷电下行先导通道的发展过程和近地区域最终击中点的选择能模拟得更好。

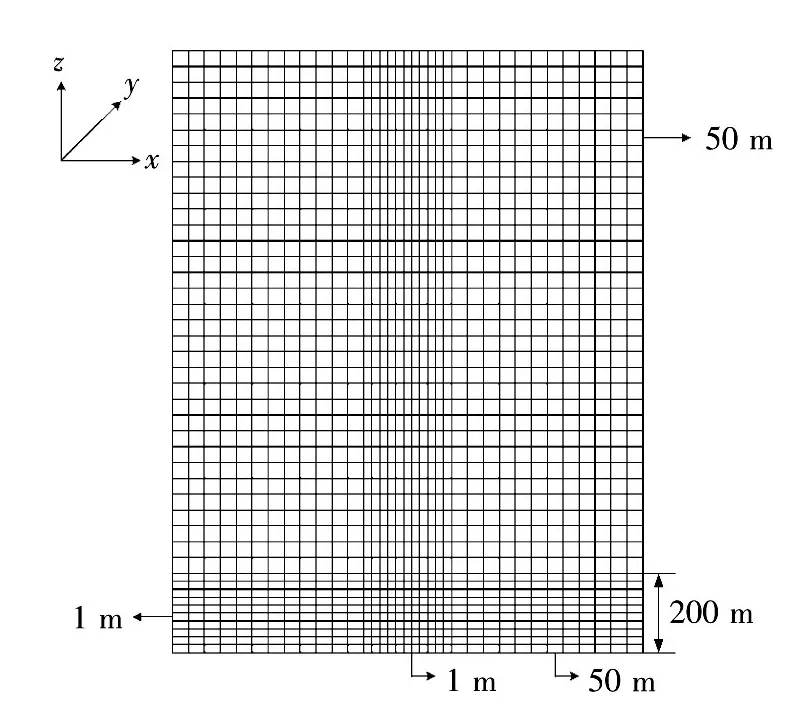
图2 三维计算空间的横切面网格剖分图Fig.2 Transverse grid diagram of three－dimensional computational space

1.3 分形参数的确定

由于自然界中各地的气候条件和地形都不同，即便对同一个地点同一个时间的一条雷电通道，不同的观测角度甚至是不同的照相技术都会得到不同的先导通道路径。在开始计算机编程模拟计算时，令η=1.1(即击穿概率与局域电场成正比)，其模拟结果得到的先导发展图像有高度分叉和扭曲的结构，由此可计算得出的分形维数平均值为D=1.75±0.02，这个模拟图案的值与实际观测到的雷电放电图案的值(D=1.70)符合得很好［7］。

1.4 下行先导通道电荷

本模型建立在对雷电发展过程中准静态场的假设基础上，因此电场的计算决定了模拟结果的准确性和合理性。采用模拟电荷法作为计算输电线路电场和先导通道电场的方法，在导线上设置模拟电荷来匹配导线电位，同时用电荷密度的形式来表达先导通道［8］。

事实上，由于技术的限制，目前对于雷电放电过程了解的还是不够充分，学者们只能通过观测回击电流的大小来反推先导发展过程中的通道电荷分布。习惯上，前人将先导通道电荷分布模型分为均匀分布、线性分布、指数分布3种模型。为了方便起见，本模型采用均匀分布的电荷分布模型，即认为先导通道包括分支通道具有统一的电荷密度，即

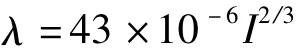
但是，该公式仅仅适用于无分支的先导通道，当先导通道分叉时应当进行修正。分支通道的存在会稀释雷电先导通道中的电荷，通过大量的模拟分析，发现带有分支的先导通道长度约为单分支的2.6倍。因此，平均电荷密度公式为

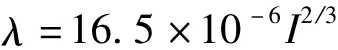
1.5 上行先导起始的判据和实现

对于上行先导起始判据，采用比较公认的Peek判据，即

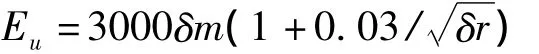
式中:m为表面粗糙度因子，r为导线半径，δ为相对空气密度。原则上，正先导上行的起始场强应满足E≥Eu≈500 kV/m，但如果地面上有多个物体上的点都满足上行先导起始判据，不能让所有可能的点都发展为上行先导起始。事实上，分形模拟和气体放电过程都具有法拉第屏蔽效应和尖端效应，如果某一热点先产生上行先导，那么就会使得周围热点处的场强大大降低。

离雷云更近的避雷线和杆塔顶端由于屏蔽作用和尖端效应，使得从他们出发的上行先导的“起跑线”比较靠前。当然这种完全屏蔽的结果显然与实际不符，因为先导通道会发生分形和扭曲，它们的发展不一定比从相导线起始的先导更“快”，所以超特高压输电线路会有绕击的可能。此外，在计算模型中将上行先导的发展速度设置为下行先导发展速度的1/3，并且设置当上行先导与下行发展的先导头部之间的平均场强达到500 kV/m时，认为最终击穿，从而确定雷击点，记录雷击点坐标。大地相比于输电杆塔很少遭受雷击，因此将击穿场强取为750 kV/m［9］。其计算流程如图3所示。

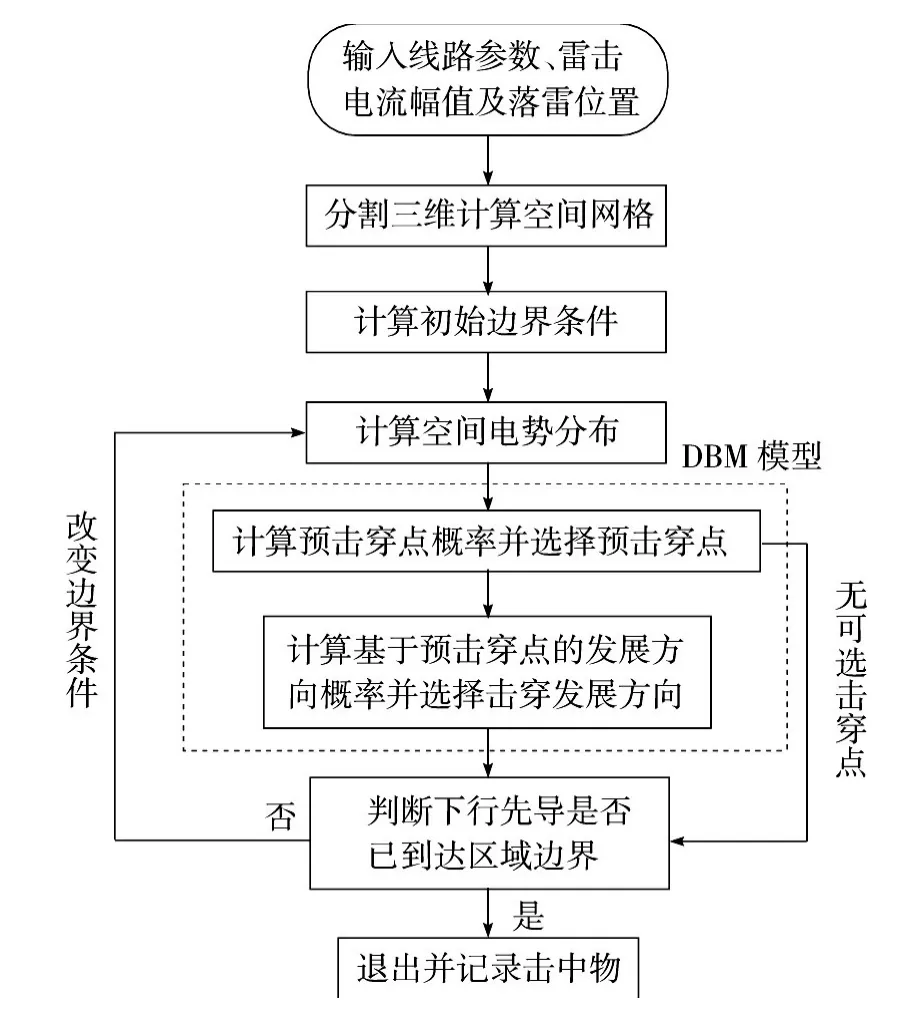
图3 改进先导发展模型的模拟流程图Fig.3 Simulation flow chart of improved leader progression model

2 雷击线路模拟场景

2.1 仿真计算模型的实现

为简化分析，在计算空间上方的雷云区域内随机选择一个起始击穿点，并假设上行先导发展与下行先导发展过程独立。本模型根据前人的研究经验将先导起始临界启动击穿值设为Einit=200 kV/m，通道内电场设置为Ein=－17 kV/m，初始击穿点坐标选择(2500，2500，5000)。梯级先导向下发展的过程中，在非近地区域，因先导头部发展方向的随机性，对最终击中点的选择影响不大，所以模拟空间的分辨率取为50 m，而随着先导逐级向下发展，在近地区域先导的每一次分形与扭曲都能对最终击中点造成影响，所以在距离地面200 m处将计算分辨率提高至1 m(如图2所示)。此区域显然覆盖了整个输电杆塔，整个模拟计算三维空间如图4所示，其中输电线路杆塔在底部的高分辨区内。整个雷电先导放电的发展过程，即先导头部不断选择向下一步发展可能热点的步进过程。数值模拟得到的雷电先导放电二维投影图样如图5所示。

图4 模拟空间示意图Fig.4 Simulation space diagram

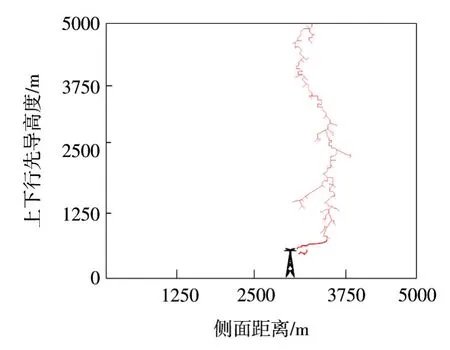
图5 分形先导发展模型模拟图Fig.5 Simulation diagram of fractal leader progression model

2.2 ±500 kV直流线路绕击跳闸率的计算

计算所采用杆塔和线路参数参考内蒙古呼伦贝尔地区伊穆±500 kV超高压直流输电线路设计，塔型如图6所示。

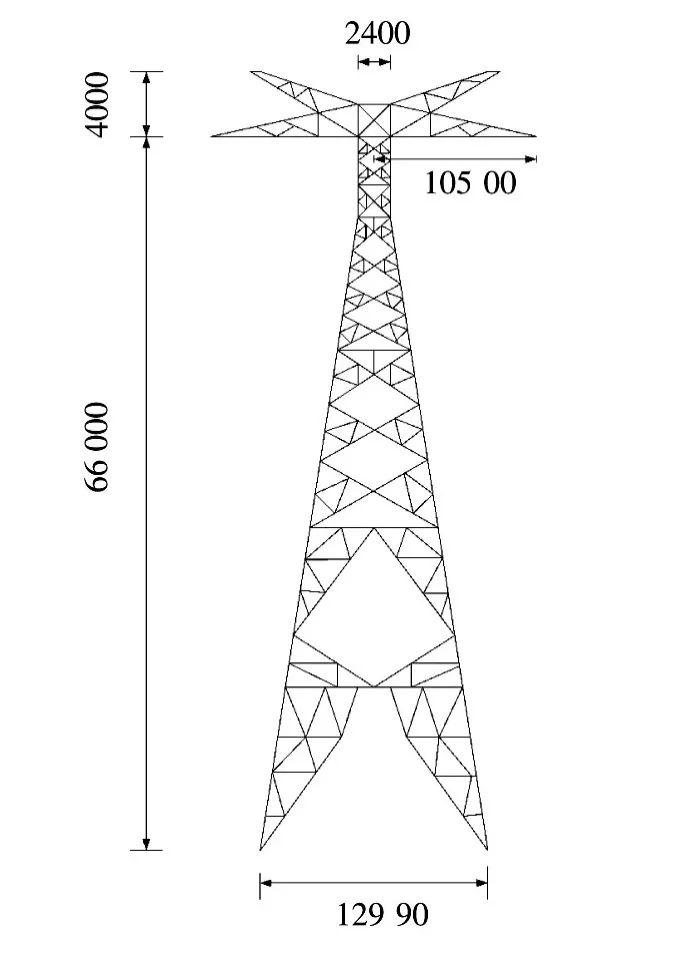
图6 500 kV直流GK52型杆塔Fig.6 500 kV DC GK52 type transmission tower

利用提高计算空间分辨率的改进先导发展模型，并根据文献［10］中对绕击率的计算方法，在模拟仿真时，设置不同的雷电流幅值与雷击点起始坐标，并记录最终的击中点坐标，数值模拟得到不同雷电流、不同雷击点起始坐标时的绕击概率分布式和绕击概率的数学期望。其中，不同雷电流在不同侧面距离时的绕击概率分布为

式中:D为不同雷击点起始坐标与杆塔的侧面距离;I为雷电流幅值。

雷电在该输电线路走廊内的落雷概率函数为

那么，将式(1)代入式(2)得到输电线路绕击概率的数学期望值为

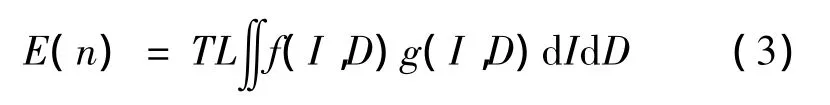
式中:L为输电线路长度，取100 km;T为时间，一般取1a。

由式(3)计算出的结果便为输电线路100 km/a的绕击次数期望值。利用提高计算空间分辨率的先导发展模型计算超特高压输电线路的绕击跳闸率，计算得出直流±500 kV线路GK52型杆塔的绕击率(保护角为0)为0.0612次/(100 km·a)。取绕击耐雷水平为20.4 kA计算得出的绕击闪络率为0.0233次/(100 km·a)，计算结果与文献［10］计算结果较接近。

3 结语

在DBM模型的基础上，提出了一种提高计算空间分辨率(近地区域的分辨率可达1 m)的改进先导发展模型，对模型中的关键参数进行了分析和讨论。利用此模型对超特高压输电线路耐雷性能进行评估，解释了传统EGM模型输电杆塔完全屏蔽的错误结论，并且给出逼真的先导通道计算模拟图形和输电线路绕击率。

［1］ 杨庆，司马文霞，冯杰.等.云广特高压直流输电线路雷电屏蔽性能研究［J］.高电压技术，2008，34(3):442－446.YANG Qing，SIMA Wenxia，FENG Jie，et al.Research on the lightning shielding performance of the Yun－Guang UHVDC transmission lines［J］.High Voltage Engineering，2008，34(3):442－446.

［2］ 钱冠军，丁一正.500 kV线路直击雷典型事故调查研究［J］.高电压技术，1997，23(2):72.QIAN Guanjun，DING Yizheng.Investigation of typical direct lightning strike incidents on 500 kV lines［J］.High Voltage Engineer-ing，1997，23(2):72.

［3］ ARMSTRONG H R，WHITEHEAD E R.Field and analytical studies of transmission lenes shielding［J］.IEEE Trans on Power App Syst，1968，87(1):270 －281.

［4］ BROWN G W，WHITEHEAD E R.Field and analytical studies of transmission lenes shielding:partⅡ［J］.IEEE Trans on Power App Syst，1969，88(3):617 － 626.

［5］ RIZK F A M.Modeling of transmission line exposure to direct lightning strikes［J］.IEEE Trans on PWRD，1990，5(4):1983－1997.

［6］ NIEMEYER L，WIESMANN H J.Fractal dimension of dielectric breakdown［J］.Physics Review Letter，1980，52(12):1033－1036.

［7］ 司马文霞，李建标，杨庆，等.雷电先导分形特性及其在特高压线路耐雷性能分析中的应用［J］.高电压技术，2010，36(1):86－91.SIMA Wenxia，LI Jianbiao，YANG Qing，et al.Fractal characteristics of lightning channels and its application to the analysis of the lightning shielding performance of UHVDC transmission lines［J］.High Voltage Engineering，2010，36(1):86 －91.

［8］ 鲁志伟，马文婧.新立变电站接地系统安全性能研究［J］.东北电力大学学报，2012，32(6):28 －32.LU Zhiwei，MA Wenjing.Grounding system safety performance of XinLi substation ［J］.Journal of Northeast Dianli University，2012，32(6):28 －32.

［9］ 魏本刚，傅正财.改进先导模型法交流特高压线路雷电屏蔽性能分析［J］.高电压技术，2008，34(9):1880 －1884.WEI Bengang，FU Zhengcai.Analysis of Lightning shielding performance of 1000 kV UHV AC transmission lines based on improved leader progression model［J］.High Voltage Engineering，2008，34(9):1880 －1884.

［10］ 伏进，司马文霞，李建标，等.基于分形理论的超特高压线路绕击耐雷性能评估［J］.高电压技术，2009，35(6):1274 －1278.FU Jin，SIMA Wenxia，LI Jianbiao，et al.Estimation on lightning shielding performance of the transmission lines based on the fractal theory［J］.High Voltage Engineering，2009，35(6):1274 －1278.