布朗运动与随机积分的起源
杨静,胡俊美
(1.北京联合大学基础部,北京100101;2.石家庄铁道大学数理系,河北石家庄050043)
布朗运动与随机积分的起源
杨静1,胡俊美2
(1.北京联合大学基础部,北京100101;2.石家庄铁道大学数理系,河北石家庄050043)
布朗运动是随机过程理论的一个特殊而重要的随机过程。通过考察和梳理随机积分理论诞生的发展过程,发现对于布朗运动的数学研究是随机积分理论的起源,并且随机积分论的发展与布朗运动的深入研究密切相关。从这个层面再次说明了布朗运动的重要性。
布朗运动;随机分析;随机积分
随机分析学,诞生于20世纪50年代,它是在随机过程一般理论及现代鞅论的产生和发展过程中逐渐形成的,是一个生命力很强的概率论分支。随机分析学不仅是研究概率论及随机过程的有力工具,而且在许多数学分支(如偏微分方程、调和分析、微分几何)、滤波与控制、通讯与动态系统及金融经济学等领域都大有用武之地。什么是随机分析学?它的创始人伊藤清(Kiyosi Itô,1915—2008)曾说过:“随机分析学是添加了随机风趣的分析学,是概率论的一个新分支。……科学的目的是以已知推断未知。如果从已得到的资料能做出唯一正确的推断,则可以建立确定性模式,分析学为此提供数学手段。当现象极其复杂,不可能做唯一推断时,只好从已知来求未知的平均,然后再求偏离平均的平均,为此应建立随机性模式,随机分析学为此提供数学手段。”其中,随机积分是对某些随机过程适当定义的各种积分的总称,它们在随机过程与随机微分方程的研究与应用中有着深刻影响。
1827年英国植物学家布朗(Robert Brown,1773—1858)在观察液体中某种植物的花粉颗粒时,观察到它在不断地作无规则运动。他做了大量的实验来寻求颗粒运动的原因,故这种运动后来被命名为“布朗运动”。随机积分的历史始于布朗运动,因此我们首先回顾一下历史上最早出现的布朗运动的3个理论模型,每一种尝试都是独立做出的。
1 布朗运动的理论模型
第一个尝试来自丹麦的天文学家蒂勒(T.N. Thiele,1838—1910),他对天文学、保险精算、数学和统计学都做出过重要的贡献,由于这些富有创造力的思想远远超前于他所处的时代,以至于他的大部分工作不能被同时代的人所理解。蒂勒的视力曾受到过严重的损害,这使得他不能再进行天文观测,于是他把对天文的兴趣转移到计算工作中来。1880年,蒂勒最小二乘法的论文(Sur la compensation dequelques erreurs quasi-systématiques par la method des moindres carrés)发表,他在研究时间序列数据时,有效地创建了一个布朗运动模型。一段时间内星星的运动、室外的温度等都是时间序列数据。由于望远镜精度的有限性,观测过程是存在误差的。蒂勒的目的是给出一个模型,可以描述一系列观测过程所带来的观测误差,从而预测真实值。他所考虑的过程本质就是微粒的布朗运动。他推导出的布朗运动具有独立的、服从正态分布的增量,方差与时间成比例[1]。虽然蒂勒也发表了这篇论文的法语版本,但是在当时人们并没有认识到它的重要性,很长一段时间里几乎没有影响。
第二个尝试来自法国的数学家巴施利耶(L. Bachelier,1870—1946)。在他19岁那年,父母相继去世,他不得不中断学业谋生,同时照顾妹妹和弟弟。在积攒了一些钱之后,1892年他开始在巴黎的索尔邦大学学习,1898年获得理学学士学位,1900年获得博士学位。由于巴施利耶曾在巴黎的股票交易所工作过,所以他的博士论文选择了用数学来研究股票市场,博士论文的题目是《投机理论》。文中在推导巴黎股票市场的动态行为时,创建了一个布朗运动的模型。巴施利耶试图将巴黎股票交易所的市场噪音(市场波动)建立模型。他意识到市场噪音(市场波动)应该没有记忆,利用中心极限定理的思想,他推断股票价格的增量应该是独立的、正态分布的。诺贝尔经济学奖得主经济学家莫顿(Robert C.Merton,1944—)曾指出,大多数金融数学的起源都可追溯到《投机理论》,另外,他认为这篇文章标志着连续时间随机过程的数学理论的诞生,及连续时间期权经济的诞生。然而,巴施利耶并没有获得同时代人的认可和重视。巴施利耶的悲剧在于他研究的内容并不属于他所处的时代,而是属于过去和未来。属于过去,是因为他研究的概率论起源于赌博,他通过考察赌博的延续形式——交易所,引进连续随机过程。属于未来,是因为不论是从概率论上还是从经济学上,他都被称为“鞅”这一概率概念的缔造者。在理解有关经济学的不确定性方面,他的思想远远超越当时的社会与文化背景[2]。
第三个尝试则来自物理学家爱因斯坦(A Einstein,1879—1955)。1905年爱因斯坦发表了论文《关于热分子运动所要求的静止液体中悬浮小粒子的运动》(On the movement of small particles suspended in stationary liquid demanded by the molecular-kinetic theory of heat),他试图根据分子的运动来解释所观测到的物质的宏观热性质,即从物质的微观结构和微观运动来说明物质的宏观性质。至于这些微观假设正确与否,还需要实验的验证,因此他更侧重说明该假设是否符合实际,此外,在文章最后他还给出了阿伏伽德罗(Amedeo Avogadro,1776—1856)常数的第一个准确测定公式[3]。这一公式在1908年被佩兰(J Perrin,1870—1942)的实验所验证。
用数学语言来说,巴施利耶和爱因斯坦给出布朗运动为:随着时间t的改变,某个质点的位置B(t)连续变化;但是对于t时刻之后的s时刻而言,质点的位移B(s)-B(t)是一个在原点附近游动的正态随机变量,其方差与时间间隔的长度成正比;而对于多个不相交的时间间隔,这些位移随机变量相互独立。因此,对于布朗运动,根据它当前的位置,我们并不能确切地知道它下一时刻的位置,而只能了解该位置的概率分布。爱因斯坦认为原来意义下的布朗运动就是这样的运动,同样,巴施利耶认为股票价格变动也应属于此类运动[4]。
2 随机积分理论基础的奠定
其实,巴施利耶和爱因斯坦对布朗运动的数学描述都不太严格。巴施利耶没能得到布朗运动的清晰图景,其思想没有得到当时人的理解,这主要是因为布朗运动的精确定义需要路径空间上的测度,而这一点直到博雷尔关于伯努利实验的经典论文1909年发表才实现。只有博雷尔、勒贝格和丹尼尔的思想出现,布朗运动才有可能建立在牢固的数学基础之上。1923年,维纳(N Wiener,1894—1964)的《微分空间》(The differential space)一文问世,布朗运动有了真正的数学描述,因此,作为一个随机过程,数学上的布朗运动也常常称为“维纳过程”。
1913年,维纳到剑桥大学访问期间追随罗素(Bertrand Russell,1872—1970)学习。罗素意识到爱因斯坦相对论对科学哲学的重要意义,建议维纳仔细研读爱因斯坦1905年发表的3篇论文,其中包括论述布朗运动的那一篇。1923年,维纳的论文“微分空间”发表,其中不仅构造了布朗运动的数学模型,而且它堪称布朗运动研究史上的一个里程碑。
爱因斯坦研究的是布朗运动的统计性态,选择的对象实际上属于可测的物理量:一个或多个颗粒的位移以及一定层面颗粒的密度。维纳则是把单个粒子的轨道看作一个集合中的一点,他选择的对象是一个(或多个)布朗颗粒所有可能运动的路线,并假定这些路线服从概率规律,进而考察这些路线或函数的空间。他从爱因斯坦物理模型的基础上抽去与实际相联系的具体内容,使之成为一个形式的躯壳,这样布朗运动就抛去了观测对象的外衣,成为一个纯粹的数学对象,由此得到了一种一般的随机过程,而不再是一个特殊现象。这样,维纳就实现了布朗运动从物理研究到数学研究的转变。
由于布朗运动的轨道样本几乎都是连续而处处不可微的,所以随机微分方程更合适的记法是积分形式的方程。随机微分方程中含有布朗运动的积分,被称为随机积分。知道了随机积分,就相当于掌握了随机微分方程的解。“微分空间”在随机过程理论中占有举足轻重的地位,是此方面最重要的著述之一,维纳把随机积分理解为所有连续轨道所在的“无限维空间”上的一种积分。为了讨论随机过程,需要函数空间上的测度和积分理论。20世纪20年代,除了维纳,其他数学家只讨论有限联合分布。在讨论依赖一个随机过程的整体轨道的泛函平均值时,他们不加证明地将其定义为依赖有限个时间点的一列近似泛函的平均值。尽管布朗运动的轨道处处不可微,维纳还是定义了平方可积函数关于布朗运动的积分,设(Bt)为一维标准布朗运动,f为(0,T)上的阶梯函数,即
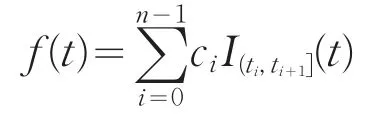
其中0=t0<t1<...<tn=T,则令
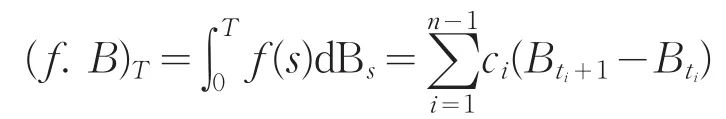
于是E(f.B)T=0,。从而映射f↦(f.B)T可以等距扩张为L2((0,T])到L2(Ω,F,P)中的线性映射。我们称(f.B)T为维纳积分,记为。这是一均值为零、方差为的高斯随机变量。如果T变动,则我们得到随机过程f.B,它是维纳不定积分[5]。维纳通过把平均值定义成丹尼尔积分,进而把布朗运动理论建立在一个牢固的基础之上。虽然他在文中研究了布朗运动,但是他的方法成为现代随机过程理论的一个典范。
随机积分的基础工作的下一步是由柯尔莫戈洛夫(A N Kolmogorov,1903—1987)完成的。随机积分理论研究的起点与马尔科夫过程理论交织在一起,并且受到其推动,柯尔莫戈洛夫在其中起到了重要作用。1931年,柯尔莫戈洛夫发表了《论概率论中的分析方法》(On analytic methods in probability theory)一文,提到并简要解释了巴施利耶对布朗运动的构造。在这篇论文中,他研究了一类连续马尔科夫过程,后来称之为扩散过程,给出了大部分他的有关马尔科夫过程的理论。值得注意的是,柯尔莫戈洛夫在文中证明了扩散过程本质上只依赖两个参数:一个是漂移速度,另一个是纯粹随机部分(扩散部分)的大小。然后,他就可以把过程的概率分布与偏微分方程的解联系起来,现在称作“柯尔莫戈洛夫方程”。柯尔莫戈洛夫推导用的是半群及其无穷小生成元,以及由此生成的偏微分方程。
柯尔莫戈洛夫研究的扩散过程满足如下条件(以一维为例):
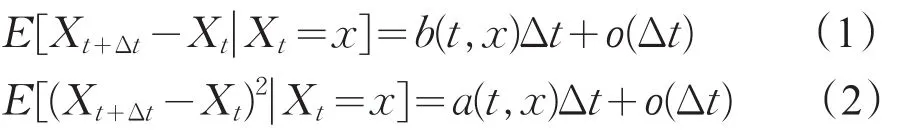
其中b(t,x)为漂移系数,a(t,x)为扩散系数。假定扩散过程的转移概率P(s,x,t,⋅)有密度函数p(s,x,t,y),并假定p(s,x,t,y)有适当的光滑性,柯尔莫戈洛夫证明了p(s,x,t,y)满足如下两个方程[5](分别称为“柯尔莫戈洛夫后向方程”和“柯尔莫戈洛夫前向方程”):
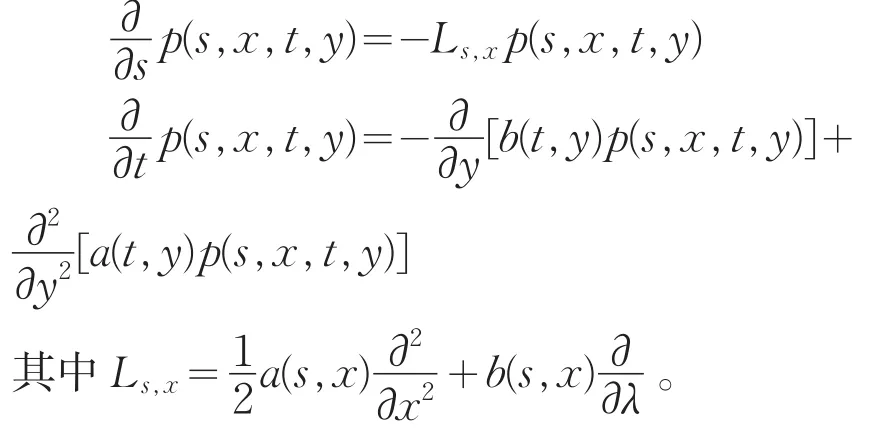
3 随机积分的创立
随机分析学研究的最初动机为通过布朗运动直接构造出扩散过程,伊藤清就是通过定义布朗运动的随机积分,进而发展出一套理论。
通常的质点运动可以用下列微分形式的微分方程来描述:
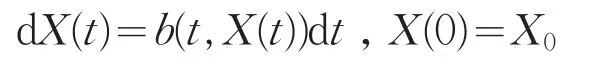
方程的左端表示质点的(微分)位移,右端表示这个位移依赖于时刻t,质点在时刻t的位置X(t)以及时间本身的(微分)流动dt。
如果质点的运动受到一个布朗运动B(t)的干扰,那么这个微分方程就演变为下列形式:
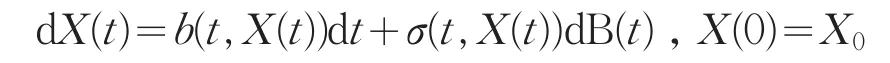
这就是伊藤清尝试在给扩散过程建造模型时构造的随机微分方程。其中后一项就代表干扰,σ(t,X(t))为干扰强度,通常也与t和X(t)有关。这个随机微分方程可改写为随机积分方程:
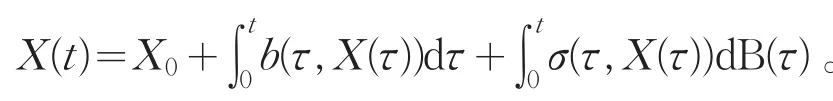
伊藤清在1944年的“随机积分”(Stochastic integral)一文中,对如何使随机微分σ(t,X(t))dB(t)有意义进行了解释。①伊藤清提到了之前S.Bernstein、柯尔莫戈洛夫、费勒的工作。伊藤清解释的关键之一在于对“标准布朗运动”来说,把“随机微分方程”dB(t)理解成均值为零、方差为dt的正态随机变量。这样在一个适当的框架下,“随机微分”dx(t)就相当于均值为b(t,x(t))dt、方差为σ2(t,x(t))dt的随机变量。
伊藤清尝试把柯尔莫哥洛夫在马尔可夫过程上的工作与自己的诠释联系起来。特别地,他想把X(t)的路径与扩散过程的转移函数联系起来。这实际上等同证明了X(t)的分布解决了柯尔莫哥洛夫的前向方程。这种尝试促成了他1951年的论文“关于随机微分的一个公式”(On a formula concerning stochastic differentials)。伊藤采用Picard逐次逼近法证明了:如果对任给T>0,b(t,x)及在 [0,T]×R上关于x满足一致Lipschitz条件及线性增长条件,则上述随机微分方程有唯一解,其中初值X0是任意给定的与布朗运动(Bt)独立的平方可积随机变量。这样,伊藤清实现了通过布朗运动构造扩散过程的设想。从此,一门崭新的概率论分支——随机分析学诞生了。
布朗运动的样本函数虽然连续,但几乎所有的都非有界变差,甚至处处不可微,因而无法按样本函数定义通常的勒贝格-斯蒂尔切斯积分或黎曼-斯蒂尔切斯积分。一般而言,黎曼-斯蒂尔切斯积分定义中的达布和不会以概率1收敛到一定的极限,但在适当要求下,达布和的均方极限存在。正是利用这一性质伊藤清定义了布朗运动的随机积分。而伊藤积分最重要的性质为著名伊藤公式,表示如下:
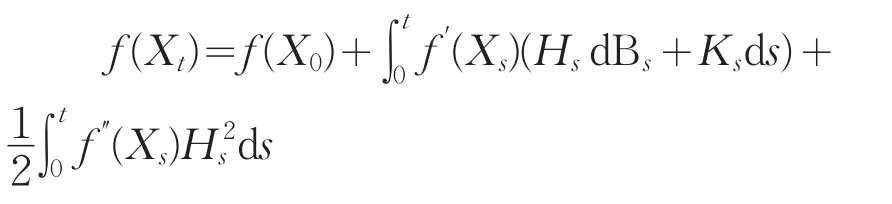
其中f是二次连续可微实函数,B(t)(t≥0)是布朗运动。该公式及其各种推广是随机分析的一个重要工具,在理论上和实践上都有广泛应用。
1987年,伊藤因此项工作荣获沃尔夫奖。在对获奖工作的评价中写道:“他的随机分析可以看作随机王国中的牛顿定律,它提供了支配自然现象的偏微分方程和隐藏着的概率机制之间的直接翻译过程,其主要成分是对布朗运动函数的微分和积分运算,由此产生的理论是近代纯粹与应用概率论的基石。”
由于伊藤清在随机分析这一新的分支所取得的开创性的杰出成就,以及随机分析在微分几何、调和分析、变分学、偏微分方程、复分析、位势论等数学分支中的应用,特别是随机分析在非数学领域,如化学、量子物理学、生物学等的广泛应用,从而使他于2006年荣获了国际数学联合会首次颁发的高斯奖。
4 结论
人们在研究随机过程理论时,可以定性地讨论一般随机过程的性质,但很难取得定量的结果。布朗运动则不然,人们可以根据布朗运动特殊的性质定量地计算出许多结果。由于布朗运动既是马尔可夫过程,又是鞅、正态过程、莱维过程与独立增量过程,人们自然想到,关于布朗运动的结果对过程是否也正确呢?因此布朗运动是随机过程理论的一个特殊而重要的随机过程。
布朗运动独立诞生于天文学、股票市场和物理学等领域,随后在数学家的手中实现了严格的数学定义、并展开了一系列的研究。为了解决有关布朗运动的一个主要问题,随着数学家研究的深入,随机积分理论由此逐步成型,并且这一理论的发展与布朗运动的深入研究密不可分。并且,随机积分在随机过程与随机微分方程的研究和应用中有着重要的作用。从这个层面上来看,随机积分理论的广阔而重要的应用愈发凸显了布朗运动的重要地位和作用。
[1]LAURITZEN S L.Aspects of T N Thiele’s contributions to statistics[J].Proceedings of the Biennial Sessions,1999,58:27-30.
[2]杨静,徐传胜,王朝旺.试析巴夏里埃的《投机理论》对数学的影响[J].自然科学史研究,2008,27(1):94-104.
[3]杨静,王丽霞.爱因斯坦与布朗运动的数学理论[J].西北大学学报:自然科学版,2006,36(1):169-172.
[4]彭实戈.倒向随机微分方程和金融数学[J].科学,1997,49(5):30-33.
[5]程民德.中国数学发展的若干主攻方向[M].南京:江苏教育出版社,1994.
Brownian Motion and the Origin of Stochastic Integration
YANG Jing1,HU Junmei2
(1.Department of Foundation Courses,Beijing Union University,Beijing 100101,China;2.Department of Mathematics and Physics,Shijiazhuang Tiedao University,Shijiazhuang 050043,Hebei,China)
Brownian motion is a special and important stochastic process in the theory of stochastic processes.This paper reviews the historical development of the theory of stochastic integration and finds out that the mathematical research on Brownian motion is the origin of stochastic integration.And this theory’s development is closely related to the profound study of Brownian motion.This aspect shows again the importance of Brownian motion.
Brownian motion;stochastic calculus;stochastic integration.
N09
A
1672-2914(2015)02-0007-04
2014-12-03
国家自然科学基金项目(11101034)。
杨静(1977-),女,河北石家庄市人,北京联合大学基础部副教授,理学博士,研究方向为近现代数学史。

