基于熵权—G1法的区域商务成本综合评价比较研究
周正柱
(上海应用技术学院,上海 201418)
基于熵权—G1法的区域商务成本综合评价比较研究
周正柱
(上海应用技术学院,上海201418)
摘要:基于熵权和G1法主客观组合赋权法,构建区域商务成本综合评价模型,并选取东部的上海和浙江、中部的安徽和河南、西部的陕西和四川6省市为评价对象,对2010—2014年期间区域商务成本进行综合评价。各区域要素成本呈现逐年上升趋势,而沿着东、中、西部逐年增长幅度呈现出递减状态。主要创新是构建基于熵权—G1组合赋权法的区域商务成本综合评价模型,并运用离差平方和方法解决了最优的组合赋权偏好系数问题。
关键词:组合赋权;商务成本;综合评价
关于区域商务成本的评价,目前主要侧重于基于要素成本和交易成本各构成要素直接比较分析[1-2]。这种分析方法只能说明各构成要素,如劳动力、土地、房屋价格及税收、政府办事效率等具体指标区域间的差异,无法说明区域商务成本总量及结构指标之间的差异。基于主观赋权法的区域商务成本综合评价[3-4],偏重于主观经验,缺乏客观性;基于客观赋权法的区域商务成本综合评价[5-6],偏重于依靠客观数据,缺乏主观性。因此,这两种方法都缺乏主客观评价的综合考虑。在现有的文献中,姚洁等(2009)[7]构建基于层次分析法的灰色关联度综合评价模型,并对西安、重庆和成都等城市总部经济模式下商务成本进行实证分析。郭彦等(2014)基于模糊数学和神经网络方法构建综合评价模型[8]。本文针对中国区域商务成本综合评价比较分析的现状和不足,将通过基于熵权—G1组合赋权法对区域商务成本评价指标体系赋权,建立区域商务成本综合评价模型,并对东部上海与浙江、中部安徽与河南、西部陕西与四川共6个典型省市,对2010—2014年数据进行实证分析,目的在于探寻东、中、西部各区域商务成本总量及结构指标变化规律及差异,为进一步揭示区域商务成本变动对企业迁移及产业转移的影响奠定基础。
一、区域商务成本综合评价指标体系构建
商务成本具有强烈的地方属性,即商务成本是一个与企业所在地相关的概念。正是各区域在劳动力、土地、公用事业等成本以及管理水平方面的差异,才导致各地商务成本的差异。而企业为生产所付出的原材料、设备、技术、运输费用以及销售费用一般不会只和企业所在地相关,这些成本缺乏“当地”的属性,所以均不纳入商务成本的研究范围内。
因此,对区域商务成本评价指标构建既要考虑到地区中各种要素对商务成本的影响,同时也要能够反映该区域中制度和外部环境对商务成本的影响。基于此设计思路及前面所述的构建原则,本文的商务成本评价指标体系主要包含以下两个方面:
第一,要素成本,主要是指商业设施及土地成本、劳动力价格水平等。
第二,交易成本,主要涉及政府运作效率、市场化程度、信息化程度、基础设施及研发能力等。
具体区域商务成本评价指标体系如表1所示:

表1 区域商务成本评价指标体系
二、基于熵权—G1法的区域商务成本综合评价模型的构建
(一)评价指标规范化处理
一般来说,不同的评价指标通常具有不同的量纲和单位,因而指标之间存在着不可公度性,所以在进行综合评价计算时,首先必须将评价指标进行无量纲化处理。商务成本所涉及指标分为正向和负向两类,对其分别进行如下无量纲化处理。
设yij(i = 1,2,…,n,j = 1,2,…,m)为第i个系统中的第j项指标的观测数据。对于正向指标,令:
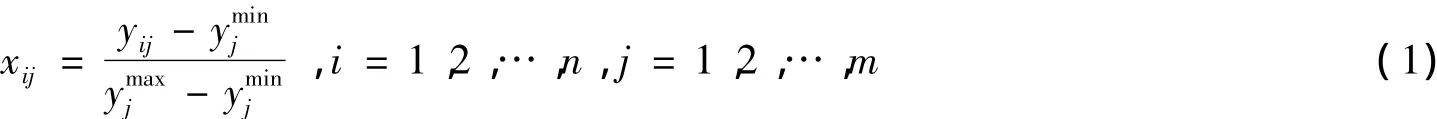
对于负向指标,令:
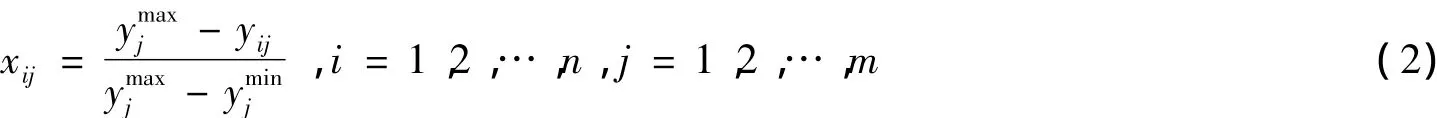
其中,ymaxj和yminj分别为第i个系统中的第j项指标的观测数据中的最大值和最小值。
(二)评价指标的组合赋权
1.评价指标组合赋权的选择
目前关于指标权重的确定方法有两类:主观赋权法和客观赋权法,在实际应用中两类方法各有利弊。为克服单一赋权方法的缺陷,最近几年来有些学者基于不同的角度提出了组合赋权方法[9-13]。在已提出的组合赋权法中,基于G1的组合赋权方法受到越来越多的关注,也为本文研究提供了借鉴。因此,本文采用熵值赋权法和G1法的组合赋权方法以及运用离差平方和最大原则来确定偏好系数[14],来确定本文综合评价模型中的指标权重。
2.评价指标客观权重确定方法:熵值法
设yij(i = 1,2,…,n,j = 1,2,…,m)为第i个系统中的第j项指标的观测数据,形成原始指标数据矩阵Y = (yij)m×n,对于某项指标yj指标值yij的差距越大,则该指标在综合评价中所起作用越大;如果某项指标的指标值全部相等,则该指标在综合评价中不起作用,在信息论中,定义第j个指标的信息熵值如下:

其中,k>0,ln为自然对数,ej≥0。pij为j项指标下第i个方案指标值的比重,即:

信息熵是系统无序程度的度量,信息是系统有序程度的度量,二者绝对值相等,符号相反。某项指标的指标值变异程度越大,信息熵越小,该指标提供的信息量越大,该指标权重就越大;反之,某项指标的指标值变异程度越小,信息熵越大,该指标提供的信息量越小,该指标的权重也就越小。所以,可以根据各项指标值的变异程度,利用信息熵这个工具计算出各指标的权重,为多指标综合评价提供依据。
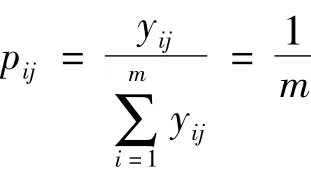
设指标熵权向量W1= (w11,w12,…,w1m)T,则第j个指标的熵权为:
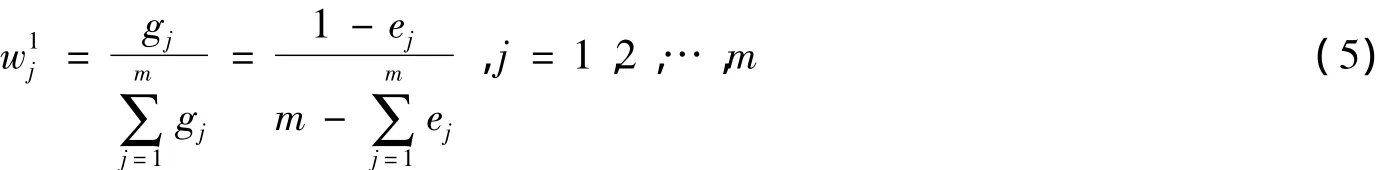
其中,gj= 1-ej为差异性系数,当gj越大时,指标越重要。
3.评价指标主观权重确定方法:基于G1法
G1法的主要思想是:首先通过专家主观判断将某一准则下的若干个指标按照其重要性程度进行排序,并给出相邻指标重要程度的比值判断,其步骤如下:
(1)专家确定指标的排序关系[15];
(2)专家给出相邻评价指标Xk-1和Xk重要性程度之比rk的理性赋值;
(3)若专家给出rk的理性赋值,则第m个指标的G1法权重为:

(4)由权重w2m可得第m-1、m-2、m-3,…,3,2个指标权重计算公式为:

因此得到的权重向量为W2= (w21,w22,…,w2m)T。
4.最优的组合赋权偏好系数确定方法:离差平方和
设指标组合权重向量为W = (w1. w2.…,wm)T,wj为两种权值组合后的第j个指标权重。将wj表示为w1
j和w2j的线性组合,即:

wj1、wj2分别表示第j个指标的熵权和G1法权重,θ1和θ2分别为两种权重组合偏好系数,表示了两种权重占组合权重的比例。通过组合赋权法来确定组合权值的一个关键问题是如何确定权重组合偏好系数。陈华友(2004)提出了基于指标离差最大化的方法来确定组合偏好系数。本文采用此种方法来计算综合评价模型中的组合权重偏好系数[16]。
令W' = (W1,W2),为一个2×m的矩阵。Θ= (θ1,θ2)T,Θ为组合权系数向量的线性表出系数组成的2维列向量。因此W可表示为矩阵形式:

这样第i个系统的多指标综合评价值可表示为:
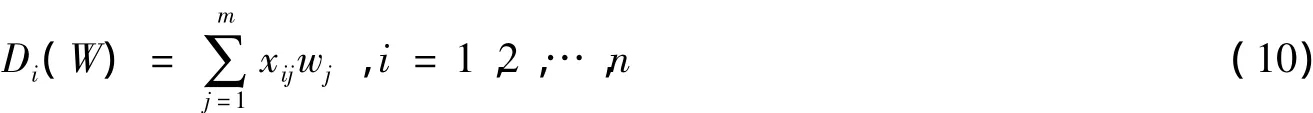
其中,xij为原始数据规范化后数据。
一般来说,Di(W)总是越大越好,Di(W)越大表示第i个系统评价越优。然而综合评价系统中,若各指标的权系数确定不当,导致各个系统的综合评价值Di(W) (i = 1,2,…,n )相互差别很小,这样将不利于各个系统的实际评价结果。所以选择组合赋权系数向量Θ的一个主要目标是使得各个评价系统的综合评价值Di(W) (i = 1,2,…,n )尽可能分散。因而本文采用各个综合评价系统的离差平方和来衡量其分散程度的一个度量标准。设第i1和i2这两个系统的综合评价值分别为Di1(W)和Di2(W),那么它们的离差定义为:
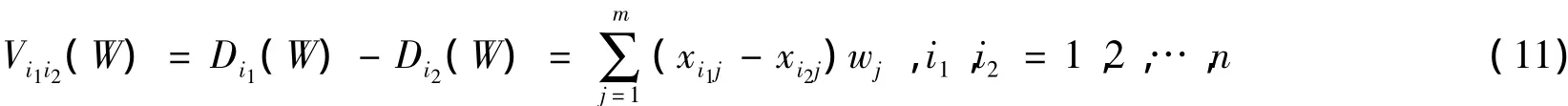
设Vi(W)表示第i个系统与其他各个系统综合评价值的离差平方和,那么得到:

根据组合赋权的权重向量偏好系数选择的基本思想,应该使得所有n个系统总的离差平方和达到最大,这样才有利于各个系统的综合评价。所以构造如下目标函数:

令m×m阶矩阵B = (bpq)m×m,其中:

因而F(W)可表示为:

确定组合权系数W = (w1. w2.…,wm)T的关键是确定权系数的线性表出系数Θ。又因为W为Θ的函数,从而目标函数F(W)就是Θ的函数,所以可将F(W)记为F(Θ)。这样参与评价的所有系统总的离差平方和的最优组合赋权问题可转化为如下最优化问题[17]:

上述非线性规划问题可进一步简化为如下的无约束优化问题:

根据矩阵理论,F1(Θ)是向量Θ的Rayleigh商,并且W'TBW'是对称矩阵,所以F1(Θ)的最大值即为W'TBW'的最大特征根,该特征根所对应的单位化特征向量Θ*即为式(13)的最优解。这样求出了Θ*,也就求出了组合权重向量W = W'Θ*。
本文通过利用两个指标值的离差平方和最大化原则,使得各个评价子系统的多指标综合评价值尽可能分散,以便更清晰地体现指标对比的差异,改善了现有相关研究中由于平均赋权而致使指标差异不明显的状况。
(三)区域商务成本综合评价思路
本文讨论了有关商务成本的综合评价过程中所要解决的关键问题,即指标权重的确定及其计算方法。权重确定以后,某一层次的指标评价结果可以通过其所属的各个子指标观测值及其权值进行加权计算获得。
设xij(i = 1,2,…,n,j = 1,2,…,m)为第i个系统(准则)中的第j项指标的规范化观测数据,由此形成规范化指标观测数据矩阵X = (xij)m×n。因此,基于熵权—G1法区域商务成本评价步骤可以概括如下:
(1)对第i个系统中的各项指标xij(j = 1,2,…,m)进行重要性排序;
(2)计算指标yij(i = 1,2,…,n,j = 1,2,…,m)的熵值ej,指标熵权W1= (w11,w12,…,w1m)T;
(3)计算指标之间的重要性程度之比rk(k = m,m-1,…,2),由此计算G1法主观权值W2= (w21,w22,…,w2m)T;
(4)计算m×m阶矩阵B = (bpq)m×m,其中bpq=∑i =1∑k =1(xip-xkp) (xiq-xkq),p,q = 1,2,…,m ;
(5)计算矩阵W'TBW'的最大特征根所对应的单位化特征向量Θ*,从而求出组合权重W = W'Θ*。其中W' = (W1,W2) ;
(6)对第i个系统或准则中的所有指标进行加权求和,得到该准则的评价值为Di(W) =∑j =1xijwj,i = 1,2,…,n,wj为第j项指标的组合权值。
三、区域商务成本综合评价实证研究
(一)评价对象及数据来源
本文主要选取上海、浙江、安徽、河南、陕西和四川6省市为评价对象。一方面考虑篇幅的限制,无法对更多省市进行全面评价,另一方面选取的样本涵盖了中国东、中、西部地区的省市。通过对这6省市的评价,基本能反映中国东、中、西部各区域商务成本在总量和结构上的差异。各指标的原始数据主要来源于2010—2014年中国统计年鉴以及上海、浙江、安徽、河南、陕西和四川6省市统计年鉴。在以下的计算过程中,以上海市为例,其他5省计算过程省略。
(二)评价指标的规范化处理
正向指标的规范化可将原始数据代入公式(1),负向指标的规范化可将原始数据代入公式(2),将上海市2010—2014年原始数据进行规范化处理,如表2中第4列至第8列所示。
(三)区域商务成本指标的熵值计算:熵值法
将6省市原始数据代入式(3)和式(4),计算评价指标的熵值,然后利用式(5)计算熵权。各评价指标的熵值列入表2中第10列所示,各指标熵权列入表2中第11列所示。

表2 上海市2010—2014年商务成本评价指标规范化得分及权重计算
(四)基于G1法主观分层赋权
1.一级指标要素成本和交易成本对目标层商务成本权重计算(1)根据专家意见得出一级指标的主观优先排序:
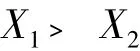
(2)根据专家意见,相邻一级指标X(k-1)与Xk的重要性程度之比rk的理性赋值为:
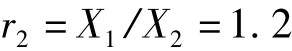
(3)把相邻二级指标的重要程度之比的理性赋值rk(k =2)代入式(6),可得第2个一级指标的权重w2= (1 +1. 2)-1=0. 454 6,将w2=0. 454 6和r2=1. 2代入式(7),则有:

所以,一级指标要素成本和交易成本G1法主观权重为: w1=0. 5454,w2=0. 454 6。
2.二级指标X11、X12对一级指标要素成本权重的计算
(1)根据专家意见得出要素成本的二级指标的主观优先排序:

(2)根据专家意见,相邻二级指标X1(k-1)与X1k的重要性程度之比r1k的理性赋值为:

(3)把相邻二级指标的重要程度之比的理性赋值r12代入式(6),可得第二个二级指标的权重w12= (1 +1. 2)-1=0. 454 6,将w12=0. 454 6和r12=1. 2代入式(7),则W11= w12×r12=0. 454 6×1. 2 =0. 545 1
所以,二级指标X11、X12对一级指标要素成本G1法主观权重为: w11=0. 545 1,w12=0. 454 6。
3.二级指标对一级指标交易成本权重的计算
(1)根据专家意见得出交易成本的二级指标的主观优先顺序为:
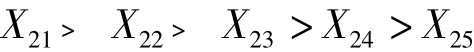
(2)根据专家意见,相邻二级指标X2(k-1)与X2k的重要性程度之比r2k的理性赋值为:
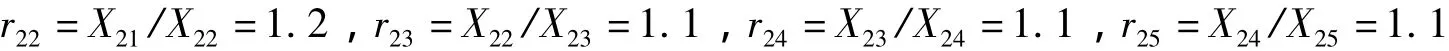
(3)把相邻二级指标的重要程度之比的理性赋值r2k(k =2,3,4,5)代入式(6),可得第5个二级指标的权重:

将w25=0. 160 3和r25=1. 1代入公式(7),则:

同理可得:

所以,交易成本的二级指标G1法主观权重为: w21= 0. 256 1,w22= 0. 213 4,w23= 0. 193 9,w24= 0. 176 3,w25=0. 160 3。
4.二级指标对三级指标权重的计算
(1)商业设施及土地成本X11
X111/X112=1. 1,X112/X113=1. 4相应的权重= (0. 390 9,0. 355 3,0. 253 8)
(2)劳动力成本X12
X121/X122=1. 3,X122/X123=1. 1相应的权重= (0. 405 1,0. 311 6,0. 283 3)
(3)能源价格X13
X131/X132=1. 2相应的权重= (0. 545 4,0. 454 6)
(4)政府运作效率X21
X211/X212=1. 2,X212/X213=1. 1相应的权重= (0. 386 0,0. 321 6,0. 292 4)
(5)市场化程度X22
X221/X222=1. 1,X222/X223=1. 1相应的权重= (0. 365 6,0. 332 3,0. 302 1)
(6)信息化程度X23
X231/X232=1. 1相应的权重= (0. 523 8,0. 476 2)
(7)基础设施X24
X241/X242=1. 1,X242/X243=1. 1相应的权重= (0. 365 6,0. 332 3,0. 302 1)
(8)研发能力X25
X251/X252=1. 2,X252/X253=1. 1相应的权重= 0. 386 0,0. 321 6,0. 292 4)
则得到目标层对指标层权重,列入表2第9列中。
(五)组合权重的计算
(1)将表2中各评价指标2010—2014年得分代入式(14)得到矩阵B ;
(2)由表2中第11列、第9列组成分块矩阵W' = (W1,W2) ;
(3)将矩阵B和W' = (W1,W2)代入式(17),计算得到Θ= (0. 6117,0. 3883) ;
(4)将W' = (W1,W2)和Θ= (0. 6117,0. 3883)代入式(9),可得组合权重,并将其列入表2第12列中。
(六) 2010—2014年6省市商务成本综合评价得分
利用式(10)分别计算二级指标、一级指标及目标层商务成本综合得分,如表3所示。以年份为横坐标,综合评价得分为纵坐标,分别画出上海市商务成本总量与结构指标得分变化曲线,如图1所示。用同样方法,可以分别计算出浙江、安徽、河南、陕西和四川2010—2014年商务成本总量及结构指标得分。
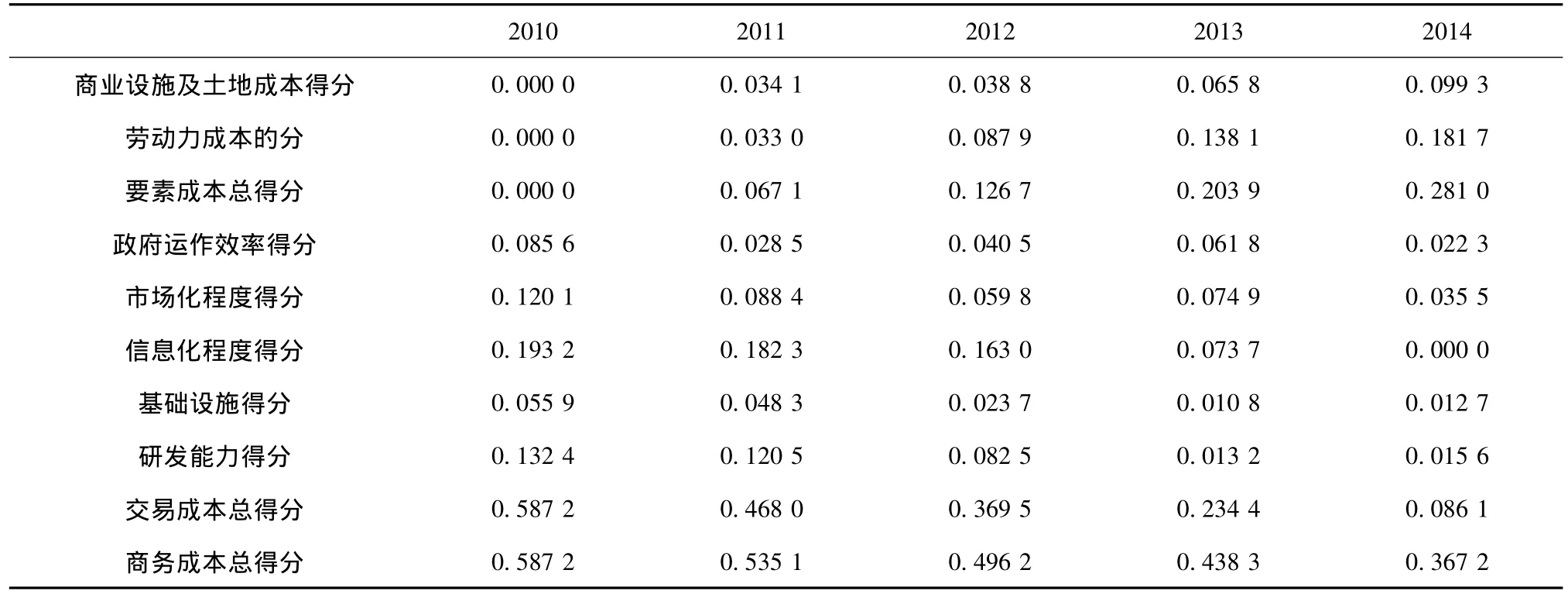
表3 上海市2010—2014年商务成本总量及结构指标得分情况
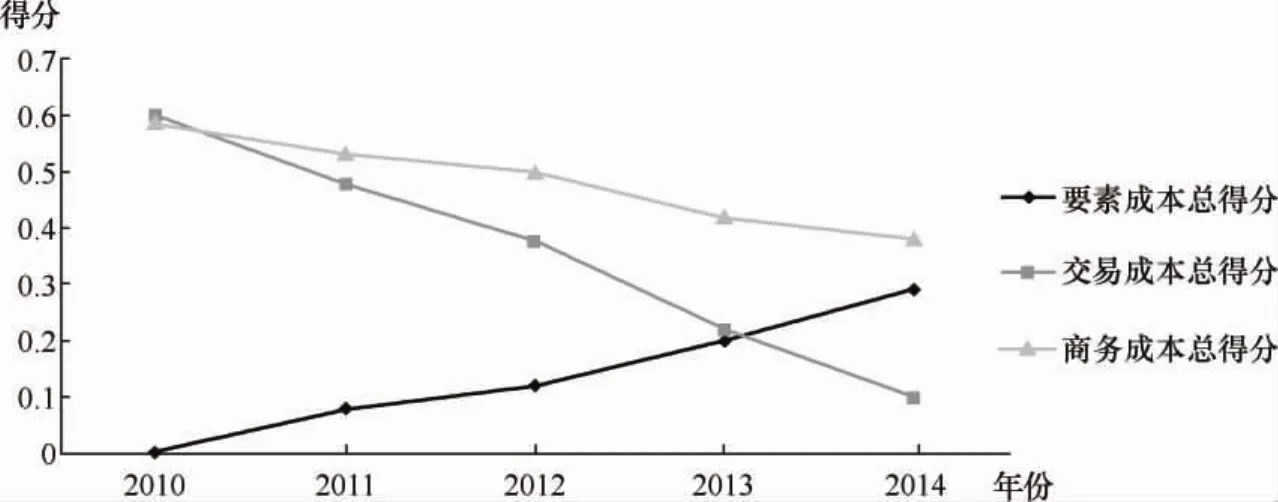
图1 上海市2010—2014年商务成本总量及结构指标评价得分曲线图
(七) 2010—2014年6省市商务成本综合评价分析
由东部的上海和浙江、中部的安徽和河南、西部的陕西和四川2010—2014年商务成本总量及结构指标得分曲线图,可知近几年区域商务成本变化呈现出如下特征和趋势:
(1)各区域要素成本呈现逐年上升趋势,但以上海和浙江为代表的东部区域增长幅度较快,以陕西和四川为代表的西部区域增长幅度相对较缓,而以安徽和河南为代表的中部区域,其中与东部区域接壤的安徽要素成本增长较快,与西部区域接壤的河南增长较慢。因此,总体上东、中、西部要素成本逐年增长幅度呈现出递减状态。这主要由于近几年中国各区域商业设施及土地成本和劳动力成本都显著增加,东部区域以上海在岗职工年平均工资为例,2010年为29 875元,而2014年就增加到42 089元,增幅达到140. 9%;中部区域以安徽人均教育支出费用为例,2010年为163. 39元,而2014年增加到424. 65元,增幅达到259. 9%;西部以四川省土地交易价格指数为例,以2009年为基准,2010年113. 18%,而2014年增加到161. 87%。
(2)各区域交易成本总体上呈现出下降趋势,但具体下降幅度有较大差异,个别区域在特定时间段还出现小幅上升情形。如以上海和浙江为代表的东部区域下降幅度较大;以陕西和四川为代表的西部区域2010—2014年下降幅度较小;而以安徽和河南为代表的中部区域,其中与东部区域接壤的安徽下降幅度较快,与西部区域接壤的河南下降幅度较慢,河南省2013—2014年交易成本不降反而上升。这主要得益于政府运作效率不断提高,市场化程度不断推进,信息化程度不断普及,基础设施不断完善,研发能力不断提高等。东部以浙江行政性收费收入占地方一般预算收入的比例这一指标为例,2010年为3. 14%,而2014年降到1. 71%;中部以河南每万人专利授权量为例,2010年为0. 34件,而2014年增加到0. 97 件;西部以陕西公路通车里程占总面积比重为例,2010年25. 61%,而2014年增加到58. 81%。
(3)以上海和浙江为代表的东部区域在2013年前交易成本大于要素成本,而2013年后表现出要素成本高于交易成本;以安徽和河南代表的中部区域和以四川与陕西为代表西部区域,交易成本虽仍然大于要素成本,但两者之间的差距明显减少。各区域交易成本与要素成本呈现出不完全相同的变化特点,这是由于区域经济发展水平、科技创新能力及市场化程度不同而导致的。以第三产业占GDP比重为例,上海和浙江2010年分别为50. 75%和39. 4%,2014年分别上升至62. 47%和51%;而安徽、河南、陕西和四川2010年分别为41. 26%、31. 8%、39. 37%和39. 35%,2014年却分别降为37. 4%、28. 63%、32. 92%和34. 78%。
(4)各区域商务成本总体上呈现出下降趋势,但下降幅度存在较大差异。以上海和浙江为代表的东部区域自2011年后下降幅度较快;以安徽为代表的中部区域及以四川和陕西为代表的西部区域商务成本曲线呈水平状,下降幅度较缓,而河南在2013年后出现商务成本小幅上升态势。这主要可能由于商务成本受区域交易成本影响较大,而导致与交易成本呈现同方向变化态势,这与我们通常理解区域商务成本变化有一定差异。实际上,通常感知的区域商务成本呈现出上升态势主要是指区域要素成本的上升,而忽视了区域交易成本的下降。或者学者们在研究中认为区域商务成本较高也往往无意中主要针对要素成本,如李锋等(2003)在分析商务成本对特定产业的影响时,列出许多商务成本很高而同时经济十分繁荣的地区,例如美国加利福利亚州的硅谷地带,尽管劳动力成本和土地成本很高,但并未对这一地区高科技产业的集聚产生很大的影响。这实际上在分析要素成本对特定产业的影响。
四、主要结论
本文的研究方法与结论总结如下:
(1)构建基于熵权—G1组合赋权法的区域商务成本综合评价模型,解决了现有的研究中客观赋权无法反映专家经验,而主观赋权无法反映客观条件变化的双重弊端。
(2)运用离差平方和方法解决了最优的组合赋权偏好系数问题,避免了针对主客观权重如何分配采用主观任意方法。
(3)各区域要素成本呈现逐年上升趋势,而沿着东、中、西部逐年增长幅度呈现出递减状态。
(4)各区域交易成本总体上呈现出下降趋势,但具体下降幅度有较大差异,沿东、中、西部逐年下降幅度呈现出递减状态。
(5)以上海和浙江为代表的东部区域在2013年后表现出要素成本高于交易成本,而以安徽和河南为代表的中部区域和以四川与陕西为代表的西部区域,交易成本虽仍然大于要素成本,但两者之间的差距逐年递减。
(6)各区域商务成本总体上呈现出下降趋势,这主要由交易成本的快速下降引起,而学者们多数研究认为区域商务成本呈现出上升态势主要是指区域要素成本的上升,而忽视了区域交易成本的下降。
参考文献:
[1]王春彦,居新平,孙明贵.上海市商务成本构成因素及趋势分析[J].华东经济管理,2007(6) :4-10.
[2]张少军,李东方.全球价值链模式的产业转移:商务成本与学习曲线的视角[J].经济评论,2009(2) :65-72.
[3]陈建军,崔春梅.商务成本与产业结构变动的动态关系研究——基于我国三大地区间的经验证明[J].上海经济研究,2010(10) : 49-57.
[4]高云虹,任建辉,周岩.基于层次分析法的中西部地区商务成本评估[J].经济问题探索,2013(11) :39-43.
[5]潘飞,马捷.商务成本的因子分析研究[J].财会通讯,2005(12) :24-26.
[6]刘斯敖.城市商务环境评价模型及其实证分析[J].北方经济,2008(6) :39-40.
[7]姚洁,郭鹏.总部经济模式下商务成本评价体系的构建及其应用[J].长安大学学报(社会科学版),2009(3) :63-67.
[8]郭彦,孙明贵.基于模糊数学和神经网络的上海市中小企业商务成本综合评价模型研究[J].无锡职业技术学院学报,2014(3) : 50-55.
[9]梁杰,侯志伟.AHP法专家调查法与神经网络相结合的综合定权方法[J].系统工程理论与实践,2001(3) :59-63.
[10]王中兴,牟琼,李桥兴.多属性决策的组合赋权法[J].应用数学与计算数学学报,2003(2) :55-62.
[11]王学军,郭亚军,赵礼强.一种动态组合评价方法及其在供应商选择中的应用[J].管理评论,2005(12) :40-43.
[12]迟国泰,祝志川.基于熵权——G1法的科技评价模型及实证研究[J].科学学研究,2008(6) :1210-1219.
[13]李刚.基于熵值修正G1组合赋权的科技评价模型及实证[J].软科学,2010(5) :31-36.
[14]王育新,刘晓冰,曹志诚.基于产业集群的高新区域竞争力评价及实证研究[J].科学学与科学技术管理,2009(11) :6-11.
(责任编辑:魏小奋)
[15]郭亚军.综合评价理论与方法[M].北京:科学出版社,2002.
[16]陈华友.多属性决策中基于离差最大化的组合赋权方法[J]系统工程与电子技术,2004(2) :194-197.
[17]王应明.离差平方和的多指标决策方法及其应用[J].中国软科学,2000(3) :110-113.
Comparative Study and Comprehensive Evaluation on Regional Business Costs Based on Entropy and G1
ZHOU Zhengzhu
(Shanghai Institute of Technology,Shanghai 201418,China)
Abstract:Based on the combination of objective and subjective weighting method of entropy and G1,the article builds the scientific evaluation model of regional business costs,and selects Shanghai and Zhejiang in the eastern,Anhui and Henan in the central,Sichuan and Shanxi in he western for the evaluation objects,and evaluates comprehensively regional business costs during 2010—2014.The main conclusions are that the regional factor costs rise,but along the eastern,central and western regions there is a decline state of growth rate year by year; transaction costs shows generally a downward trend,but along the eastern,central and western regions there is a decline state of decreasing rate.
Keywords:portfolio weighting; business costs; comprehensive evaluation
作者简介:周正柱(1971—),男,上海应用技术学院副教授。
基金项目:中国浦东干部学院2014年度长三角改革发展研究课题“加快推进产城融合路径研究”(CELAP2014-YZD-14)
收稿日期:2015-05-27
中图分类号:F714
文献标识码:A
文章编号:1008-2700 (2015)05-0037-10

