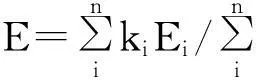电力机车优化操纵国内外研究算法综述



电力机车优化操纵国内外研究算法综述

周继续1，贺德强1，姚晓阳2，向伟彬1，陈二恒1

(1.广西大学 机械工程学院，广西 南宁 530004；

(2.南车株洲电力机车研究所有限公司，湖南 株洲 412001)

摘要:针对电力机车优化操纵国内外研究现状及其所用算法进行研究，分析不同算法在求解电力机车最优操纵方法时的运算过程，论述不同算法在求解机车最优操纵方法的实用性、推广性及其优势与不足，为进一步寻找电力机车优化操纵更优算法、探索机车更节能操作方法和研发机车模拟操作指导系统提供依据。

关键词：电力机车；优化操纵；研究现状；算法分析

电力机车优化操纵方法的研究，既可以用于指导机车在安全、正点的前提下，最大限度的节约能源，也是建立司机模拟操纵指导系统，寻找机车最优操作方法的重要依据。迄今为止，国内外铁路科研工作者以多种形式和不同方法相继对机车优化操纵问题展开了一系列的研究[1]，并取得了许多成果。主要优化算法包括遗传算法[2]、非线性有约束的动态最优化方法及自适应原理[3]、牛顿迭代法[4]、定界搜索法[5]、模拟退火算法(SA)[6]和模糊控制算法[7-8]等。国内外对其研究所用算法虽有不同，但主要是通过设计操纵模型[9]和最优控制模型[10]，进而建立目标函数，再结合机车乘务人员的实际操纵方法和机车实际运行环境，求得最优操纵方法。本文主要通过对电力机车优化操纵的国内外研究现状及其所用不同算法进行研究，分析不同研究算法在机车优化操纵中的优缺点，为探索电力机车更优操纵方法提供依据。

1机车优化操纵国内外研究算法应用

列车在实际运行过程中，一般包括起动加速、匀速、惰行和制动几个阶段，其典型的速度曲线可用图1描述。

图1　列车牵引、惰行、制动组合运行示意图Fig.1 Traction, coasting, brake composite sketch map of running train

列车在实际运行中，受到基本阻力∑W基、坡道阻力∑W上坡-∑W下坡、曲线附加阻力∑W曲、隧道空气附加阻力∑W隧以及一些必要∑Ek必和不必要的制动阻力∑Ek必等影响，其运行过程的功能表达式可用下式表示：

∑(Nk·t)=∑W基+∑Ek不+

(∑W上坡-∑W下坡)+∑W曲+∑W隧

(1)

其中,∑(Nk·t)为总轮周功。

机车优化操纵的研究，大部分是依据图1以及列车运行的功能表达式，探索减少不必要制动损耗、寻找最佳惰行点[11]以及控制列车运行时间[12-14]的节能控制。因此，可以通过建立列车运行能耗模型，确定节能控制模型的目标函数，通过仿真分析[15]，求出最优解，进而确定最优操纵方法。

1.1遗传算法

在国内外列车优化操纵研究中，遗传算法是使用最普遍的一种算法，其分支较多，因此方法也较灵活，主要包括坡道三分法确定最佳惰行点[16]，多种群遗传算法计算能耗最优解[17]，建立惰行控制模型[18]，建立速度时间模型[19]及四组染色体求解最优法[20]等。

从式(1)可以看出，列车节能控制模型是一个复杂的多约束、非线性的过程，不易精确求解，且求解过程繁琐、耗时。而遗传算法作为一种全局优化搜索算法，以其编程简单、鲁棒性强、适于并行处理等优点，成为求解机车优化问题的重要方法。

首先确定机车的各项参数，预先设定最大繁殖代数M为停止准则，用基因Xi表示手柄位变化，手柄位具体值可用Ni表示，对染色体进行二进制编码和解码，其次选择合适的初始种群(如计算机随机产生的m个染色体)和适应度函数，再对选取的染色体进行选择、交叉和变异，直至满足停止准则，求得机车实际运行条件下的最优解，具体算法过程如图2所示。

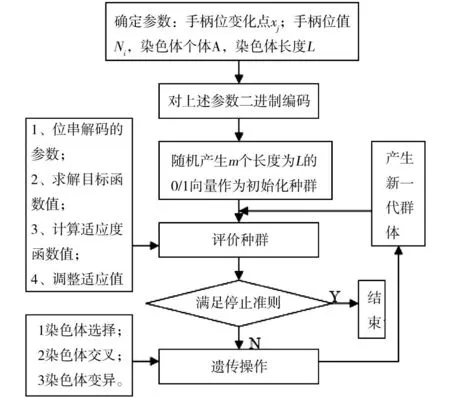
图2　遗传算法求机车节能最优解设计过程Fig.2 Genetic algorithm for optimal design of train energy saving

1.2非线性有约束的动态最优化方法

理想条件下，列车运行的优化操纵问题可用如下方程组表示[21]：

状态方程:ds/dt=v,dv/dt=120f

(2)

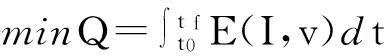
(3)

约束条件: 0≤S≤S0, 0≤v≤vmax

(4)

边界条件: S(t0)=0, v(t0)=0

S(tf)=S0, v(tf)=0

(5)

式中：v为机车运行速度；t0，tf分别为机车运行起始和终止时间；f为单位合力；s为运行距离；s0为区间距离；E为单位小时耗电量；I为司机手柄位；E(I,v)为在I手柄下以速度v运行时的单位时间能耗；vmax为限制速度。

由以上方程分析可知，机车优化操纵是一个非线性、有约束和边界条件的动态寻优过程。通过设计嵌入式测控装置，建立起机车在实际运行条件下的智能实时监测模块，再通过测控装置中的反馈模块，将采集的机车实际运行位移量Sr(t)和速度量vr(t)与机车在理想条件下运行的位移量Sm(t)和速度量vm(t)作比较，把优化后的手柄修正位ΔI反馈给司机，进而调整机车手柄位，达到节能的目的。上述智能操作优化模型原理如图3所示。

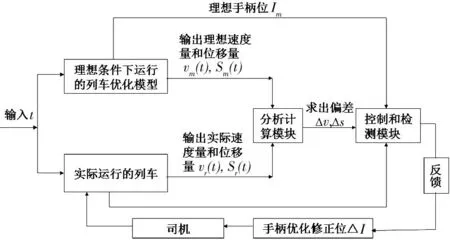
图3　智能操作优化模型原理图Fig.3 Intelligent operation optimization principle diagram model

1.3牛顿迭代法

机车正常运行过程中，假设机车单位能耗为f，运行速度为v，总能耗为J，站间距离为L，运行总时间为T，运行位移为s，制动加速度ab，则运动方程可表示为：

ds/dt=v

(6)

(7)

r(v)=a+bv+cv2

(8)

整个过程中产生的能耗为[4]：

(9)

τk+1=tk+1-tk

(10)

约束条件为：

(11)

(12)

其中：a，b，c，H为常数；r(v)表示阻力加速度；fj(k+1)为单位能耗；dk+1为τk+1时间间隔内列车前行的距离。

引进新函数Ф(τ)，φ(τ),令：

Φ(τ)=L-d(τ)

(13)

φ(τ)=t(τ)-T

(14)

则求解能耗J的过程转化为寻找J在附加Ф(τ)，φ(τ)条件下的极值点过程。因此，采用拉格朗日乘数法求解较简便，引入拉格朗日乘数因子λ，μ，定义拉格朗日函数为：

J(τ,λ,μ)=HJ(τ)+λΦ(τ)+μφ(τ)

(15)

求J(τ,λ,μ)对τ的一阶偏导数，令它们等于0，并与附加条件联立，即：

Jτ(τ,λ,μ)=HJ(τ)+λΦτ(τ)+μφτ(τ)=0

Φ(τ)=0

φ(τ)=0

λvk-μ=vkr(vk)

(16)

设λvk-μ=vkr(vk)解分别为vmax, vmin,结合式(16)，解出：

(17)

(18)

设n=2q,考虑优化方案，建立时间和距离函数为[4]：

(19)

(20)

其中：

fj(1)=fj(3)=…=fj(2q-1)=G

fj(2)=fj(4)=…=fj(2q)=0

v1=v3=…=v2q-1=vmax

v2=v4=…=v2q=vmin

整个行程消耗的能量为[4]：

(21)

因此，只需对式(19)～(20)求解，寻找唯一的一对数(vmin-q,vmax-q),使得τq(vmin,vmax)=T,δq=(vmin,vmax)=L成立，再把这对确定实数(vmin-q,vmax-q)代入式(21)，即可求出列车运行过程的最小能耗。相应求解可选择牛顿迭代法，具体求解过程如下：

取G=1,fj(n+1)=-1(-1表示制动)，定义新函数：

ζ(vmin)=τq(vmin, vmax)-T

(22)

ω(vmin)=δq(vmin, vmax)-L

(23)

利用牛顿法求解非线性方程ζ(vmin)=0和

ω(vmin)=0，由牛顿迭代公式：

(24)

取初始值vmin=v1,vmax=v2(单位为m/s,v1<L，则应减少v2的值，直至δq(v1,vn)=LnL,确定相应的vm的值，再取(vn,v2)或(v2,vm)中点vp，使Vmax=vqm/s,利用MATLAB仿真程序，直至当Vmax=vkm/s时，有τq(vmin,vmax)=T；δq(vmin,vmax)=L，此时，假设依据仿真程序可求得vmin=vim/s，即求出了符合约束条件的唯一一对实数(vi，vk)，再将这对实数带入能耗方程(21)，求得相应的能耗即为最小能耗，相应的操作方法即为最佳操作方法。

1.4定界搜索法

列车在实际运行中，其速度-距离曲线是连续动态的，因此列车优化操纵是一个非线性，有约束条件和边界条件的动态化问题，直接分析很难求出最优解。为此，可以通过将曲线离散化，并根据具体条件确定列车转入惰行时的速度，构造优化模型[5], 再经过筛选，用定界搜索法求出列车运行最优控制方法。该方法的具体步骤如下：

设优化模型中有m个制动处，每个制动处i有ni个方案，第i制动处第j方案可表示为xij。用数学模型表示为：

(25)

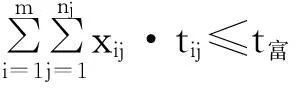
(26)

(27)

式中：xij为第i制动处第j方案，取1或0，取1代表该方案被选中，取0则表示未被选中；Eij为用xij方案能节省的能耗；tij为xij方案所多花费的时间。

分析已建立的数学模型可知，当制动处i固定时，tij和Eij均随j增大而增大，因此当j取最大值时，得出tin和Ein最大，其中Ein最大表示采用xij方案能节省的最大能耗，此模型为线性0—1优化模型，可用矩阵求解。

图4　定界搜索法运算过程Fig.4 Bound search method for computing process

1.5模拟退火算法(SA)

列车在任意时刻运行时，需要克服各种阻力做功，相关受力分析可用图5所示。

由图5分析可知，列车在任意t时刻，某一车厢受力分析可用数学表达式表示如下：

mi·ai=Fi-Ffi-f曲i-ζi-1(vi-vi-1)-

ζi(vi-vi-1)-ki-1(xi-xi-1)-ki(xi-xi+1)

(28)

车厢牵引力：Fi=(Pi·ηi)/vi

(29)

黏着牵引力：Fui=mi·g·ui·cosθi

(30)

最大牵引力：Fmaxi=min(Fi,Fui)

(31)

限制条件：vi≤v限，T≤T富,ai

(32)

图5　列车运行任意时刻受力分析图Fig.5 Force analysis of train operation at any time

在任一时刻，由以上公式可解出以下参量。

机车总牵引力：

(33)

机车基本总阻力：

(34)

电力机车牵引功率：

Pi=f串(vi,θi,ki)·vi/ηi

(35)

机车运行总能耗：

(36)

其中:ξ是阻尼系数；k为车厢间电力连接器弹性系数；g为重力加速度，g≈9.81 m/s2。θ为垂直轨道坡度；λ为水平轨道曲率；p单为机车发动机单位功率。

目标函数Q总是一个非线性，有限制约束条件和边界条件的动态方程，采用常规方法很难直接求解Q总的最小值，而模拟退火算法以其求解过程与初始值、初始状态无关、并行性和渐进收敛性等特点成为求解Q总的一种较好的全局优化算法。具体求解过程如图6所示。

图6　模拟退火算法求解机车运行最优解过程Fig.6 Simulated annealing algorithm to solve the locomotive running process of the optimal solution

1.6模糊控制算法

模糊控制算法(Fuzzy control algorithm)是利用Fuzzy关系的矩阵运算来处理不同论域中Fuzzy子集间关系的非线性智能控制方法。列车在运行过程中，考虑惰行点位置sc，起动加速度at，制动加速度ab，运行时间t，可建立如下能耗模型：

E=f(sc,at,ab)min(tmin

t=h(sc,at,ab)

(37)

利用模糊控制求解能耗E，需要将变量sc,at,ab模糊化，变成相应论域中的Fuzzy子集。为此，引进惰行系数kc，牵引系数kt，减速系数kb，其中

kc=vc-min/vc-max

kt=Fr/Fr-max

kb=ab/ab-max

式中：Fr，Fr-max分别为机车运行最小和最大有效牵引力。

则式(34)可转化为：

E=f(kc,kt,kb)min(tmin

t=h(kc,kt,kb)

(38)

依据列车运行经验，定义kc为区间[0.5,1]中任一实数，kc所选的实数组成集合A，kt，kb从11个典型牵引和制动控制的离散位置[0.5,0.55,0.6,0.65,0.7,0.75,0.8,0.85,0.9,0.95，1.0]中选择，kt，kb所选的数值分别对应集合B和C，kc,kt,kb的不同组合求出能耗E的数值对应集合D，利用模糊关系R，即：

(39)

式中符号“×”按下式定义[22]

fR(kc,kt,kb,E)=

Vc,t,b[f(kc)∧f(kt)∧f(kb)]∧f(E)

其中kc∈A, kt∈B, kb∈C,E∈D

因此当输入量取kc,kt,kb时,根据Fuzzy算法合成，输出量E的集合D为：

D=(kc×kt×kb)·R

(40)

其中符号“·”为模糊矩阵的矢量乘积。

图7　模糊控制算法求解流程图Fig.7 Flow chart used fuzzy control algorithm

2列车优化操纵算法分析

国内外学者在研究机车优化操纵时，均能巧妙利用各类算法求解机车最低能耗和寻找最优操作方法，但在利用各类算法分析计算时，很少有将列车实际操作方法中的制动位、运转位和恒速位的手柄信息参数列入考虑范围，且各类算法在计算求解时也会因自身的局限性对计算结果造成一定的偏差，因此有必要对机车优化操纵的各类算法的优缺点进行分析。

遗传算法作为全局寻优算法，以其编程简单、鲁棒性强、适于并行处理等优点在列车的能耗求解中得到广泛应用，但我们经过分析可知，列车优化操作研究作为一个复杂的多约束，非线性的求解过程，单一的遗传编码无法系统的全面描述出优化问题的约束条件，且遗传算法在运算时容易出现过早收敛，算法的精度、运算复杂性和可行度也无法进行定量分析，对实验结果会造成一定偏差；非线性有约束的动态最优化方法虽综合考虑了手柄信息等实际操作方式，且建立了具有实时预报和检测功能的智能优化操作模型，但此方法更多的是依靠机车司机操作经验，缺乏一定的理论依据和指导意义；牛顿迭代法通过拉格朗日乘法给出目标函数，运用牛顿迭代法求解目标函数后，再将求解结果带入能耗函数计算，迭代效果较好，能够满足要求，但在求解目标函数时，无法保证设置初始值的合理性，因此需要多次试探求解，每个初始值均需要运用牛顿迭代法对目标函数进行求解并分析，因此增加了求解的难度并延长了求解时间；定界搜索法通过将列车速度和位移曲线离散化，再运用[0.1]矩阵的特征运算求解，方法简单灵活，但在建立能耗模型时，由于此法更多的依靠实际操作经验，且需要综合考虑列车实际运行牵引工况和合理设计制动变化区间，因此很难建立相应的稳定能耗模型，对以后建立能耗模型的研究缺乏理论指导；模拟退火算法容易理解、应用灵活、计算过程简单并且一般不受初始条件约束，能够很好地求解列车运行的能耗模型，对以后机车优化操纵的进一步研究具有一定的理论指导意义，但该法收敛速度较慢，执行时间较长，因此无法满足算法运算的高效性要求；模糊控制算法能够简化所求系统的复杂性，特别适用于求解非线性、多约束的控制系统，具有较好的鲁棒性、适应性、强健性和容错性，应用于求解列车运行能耗时，能够很好地把时间和能耗统一在一个目标函数中，求解结果更加系统和科学，但模糊控制算法的设计尚缺乏理论指导，难以获得模糊规则和隶属函数，因此无法保证模糊控制运算过程的稳定性和精度。

此外，随着我国铁路向重载、高速方向发展，以及铁路运输中电力机车所占比重不断增大，铁路运输中电能消耗成倍增长，而目前国内外对机车优化操纵的研究大都停留在内燃机车时代，不能很好地为我国日益增加的电力机车铁路运输系统服务，因此对电力机车优化操纵的研究不仅必要而且迫在眉睫。同时，现今的机车优化操纵研究大都停留在理论指导层面，对于实践性很强的列车操作虽具有一定的理论指导意义，但很难应用于实际操作中，对此也需要进一步的深化研究。

3结论

1)探索和建立能够解决把电力机车手柄位、运行时间、惰行、牵引和制动等各项参数统一在一个目标函数中的算法程序，提高电力机车优化操作求解值的精确性；

2)列车在一定路段正点运行时求解最佳牵引、运行速度、制动和能耗的算法实现，机车模拟操作指导系统的研究与开发，从而为列车的实际运行提供理论和实践指导；

3)探索人工智能操作与机车自动驾驶系统(ATO)相结合的人工智能优化操纵方式，在ATO系统指引机车运行的基础上，通过人工智能获取运行路线各项实际参数，从而根据机车实际运行状态微调修正手柄位，更好地促进机车安全、准点、节能运行。

参考文献：

[1] 金炜东. 列车节能操纵优化方法研究[J]. 铁道学报, 1997, 19(6):58-61.

JIN Weidong. Study on optimization method of train operation for saving energy[J]. Journal of the China Railway Society, 1997, 19(6):58-62.

[2] Chang C S, Xu D Y. Differential evolution based tuning of fuzzy automatic train operation for mass transit system[J]. IET Electric Power Applications, 2001, 147(3): 206-212.

[3] 李平,张健,周震,等. 机车智能优化操纵向导装置的研制[J]. 仪器仪表用户,2006,13(1):25-27.

LI Ping, ZHANG Jian, ZHOU Zhen, et al. The study of an intelligent guide equipment for optimization operation of locomotive[J]. Instrumentation Users, 2006,13(1):25-27.

[4] 程家兴.列车节能操纵中最优方案的算法[J]. 微机发展,1999(2): 1-4.

CHENG Jiaxing. Train saving energy operation optimal algorithm[J]. Microcomputer Development, 1999(2):1-4.

[5] 毛节铭,王海鹰. 列车优化操纵计算机辅助系统[J]. 西南交通大学学报,1995, 30(3) : 317-322.

MAO Jieming, WANG Haiying. Train optimization operation computer aided system[J]. Journal of Southwest Jiaotong University, 1995,30(3)：317-322.

[6] Kitae K M. Optimal train operation for minimum energy consumption considering track alignment, speed limit, and schedule adherence[J]. Journal of Transportation Engineering, 2011，9(3): 665-674.

[7] Bocharnikov Y V. Optimal driving strategy for traction energy saving on DC suburban railways[J]. IET Electric Power Applications, 2007, 1(5):675-682.

[8] Earl Cox. Fuzzy modeling and genetic algorithms for data mining and exploration[M]. Morgan Kaufmann, 2005.

[9] 杨浩. 模型与算法[M]. 北京: 北方交通大学出版社, 2002: 195-203.

YANG Hao. Model and arithmetic[M]. Beijing: Northern Jiaotong University Press,2002:195-203.

[10] 付印平,高自友,李克平. 路网中的列车节能操纵优化方法研究[J]. 交通运输系统工程与信息, 2009, 9(4):90-96.

FU Yinping, GAO Ziyou, LI Keping. Optimization method of energy saving train operation for railway network[J]. Journal of Transportation Systems Engineering and Information Technology,2009, 9(4):90-96.

[11] Wong K K, Ho T K. Coast control for mass rapid transit railways with searching methods[J]. IET Electric Power Applications, 2004,151(3): 365-376.

[12] Hwang H S. Control strategy for optimal compromise between trip time and energy consumption in a high-speed railway[J]. IEEE Trans Syst Man Cybernet, 1998, 28(6):791-802.

[13] Albrecht T, Oettich S. A new integrated approach to dynamic schedule synchronization and energy saving train control[C]// Computers in railways VIII John J. Allan. WIT Press, 2002: 847-856.

[14] Albrecht T. Reducing power peaks and energy consumption in rail transit systems by simultaneous train running time control[C]// Computers in railways IX John J. Allan.WIT Press,2004: 885-894.

[15] Kim K, Chien S. Simulation-based analysis of train controls under various track alignment[J]. TRANSP ENG-ASCE, 2010, 136(11):937-948.

[16] 李玉生,侯忠生. 基于遗传算法的列车节能控制研究[J]. 系统仿真学报, 2007, 19(2): 384-387.

LI Yusheng, HOU Zhongsheng. Study on energy-saving control for train based on genetic algorithm[J]. Journal of System Simulation,2007,19(2):384-387.

[17] 刘炜,李群湛,郭蕾,等. 基于多种群遗传算法的城轨列车节能运行优化研究[J]. 系统仿真学报, 2010, 22(4):921-925.

LIU Wei, LI Qunzhan, GUO Lei, et al. Study of urban railway energy saving train control optimization based on multi-population genetic algorithm[J]. Journal of System Simulation, 2010,22(4):921-925.

[18] 马超云,毛保华,梁肖,等.地铁列车节能运行惰行控制研究[J].交通信息与安全,2010, 2(28):37-42.

MA Chaoyun, MAO Baohua, LIANG Xiao, et al. The study of energy saving control operation line in subway train[J]. Journal of Transport Information and Safety, 2010, 2(28):37-42.

[19] 程锦松.一种解列车节能操纵问题的改进算法[J]. 微机发展,2001(2): 8-11.

CHENG Jinsong. An algorithm for solving the energy-saving train control problem[J]. Microcomputer Development,2001(2):8-11.

[20] Seong-Ho Han. An optimal automatic train operation(ATO) control using genetic algorithms(GA)[C]// Proceedings of IEEE, 1999:360-362.

[21] 赵爱菊.机车优化操纵的微机指导系统[J]. 铁道学报,1990,12(1):1-9.

ZHAO Aiju. Computer instruction system of locomotive operation optimization[J]. Journal of the China Railway Society, 1990,12(1):1-9.

[22] Yang Y, Wang X P. On the convergence exponent of decomposable relations[J]. Fuzzy Set and Systems, 2005(151):403-419.

Domestic and international algorithm analysis

of electric locomotive operation optimization

ZHOU Jixu1, HE Deqiang1, YAO Xiaoyang2, XIANG Weibin1, CHEN Erheng1

(1. College of Mechanical Engineering, Guangxi University, Nanning 530004, China;

2. CSR Zhuzhou Electric Locomotive Research Institute Co., Ltd. Zhuzhou 412001, China)

Abstract：This paper focuses on algorithm investigation which aims at electric locomotive operation optimization research both at home and abroad. The operation process of different algorithms was analyzed, which was used in solving the optimal operation method of electric locomotive. Meanwhile, the practicability, popularization, the advantages and disadvantages of different algorithms were discussed to resolve this problem. Thus the research findings obtained in this paper can provide a basis for further study in finding better methods for electric locomotive operation optimization, exploring more energy-efficient operation method for locomotive and establishing locomotive simulation operation guidance system.

Key words：electric locomotive; optimum handling; research status; algorithm analysis

中图分类号：TP391.9;U260

文献标志码：A

文章编号：1672-7029(2015)01-0177-07

通讯作者：贺德强(1973-)，男，湖南桃江人，教授，博士，从事机车车辆故障诊断与智能维护、列车网络与控制；E-mail：hdqianglqy@126.com

基金项目：国家自然科学基金资助项目(51165001)；广西自然科学基金面上资助项目(2013GXNSFAA019297)

*收稿日期：2014-07-20