高压方箱电机内部三维温度场计算与分析

张胜男，王春瑞，于京平

(佳木斯电机股份有限公司，黑龙江佳木斯154002)

0 引言

空冷却方式被旋转电机普遍采用，即:通过风扇作为激励源强迫空气流动来冷却电机。电机的通风效果影响着电机的温升、效率、运行状态等诸多方面，尤其随着电机容量的不断加大这种影响会越来越大。如果电机内部温升过高将会导致绝缘出现分层、脱壳、老化等现象，从而使绝缘的介电性能下降，进而引发电机内部的各种放电、短路故障，增加了电机发生故障的概率。所以如何使电机产生的热量能被有效控制，在电机的设计中非常重要，通过对电机通风散热系统的正确分析，可以实现对电机温升的控制，确保电机的可靠性，对于材料利用率的提高、成本的降低也都起着非常重要的作用［2］。

本文旨在通过对电机内部温度场的计算分析，进而掌握电机在运行时温度分布情况，从而为电机风路的优化提供必要参考依据。

1 原理和方法［3］

1.1 传热的基本定律

热量总是从高温向低温方向传导。至于热流密度，即单位时间内通过单位等温面的热量，则与各点在等温面的法线方向上的空间温度变化率或即各点的温度梯度成正比

式中，q—热流密度;λ—比例常数，即热导率。

1.2 热传导方程

计算热传导问题是较为复杂的问题，例如计算绕组导体或铁心沿轴向的温度分布时，则不能采用近似的“路”的概念，而仍需要场方程，即需要建立温度场与热源之间的关系式。这种关系式成为热传导方程，它是建立在热传导定律和能量守恒原理的基础上的。

设想从热源温度场的介质中分离出一个体积元dv，则根据能量守恒原理:在一定时间内，这个体积元内所产生的热量Φ1应等于同一时间内从这个体积元表面传导出去的热量Φ2与留在体积内的热量Φ3之和，即

假定介质在单位时间内，单位体积中所产生的热量为p，p 可以是空间及时间的函数，则在dt时间内，介质中所产生的热量为

在同一时间内，被介质所吸收的热量为

式中，c—比热容。

在同一时间内，从介质的全表面传导出去的热量为(假定各向热导率相等)

式中应用了奥式定理，又因为热量从高温流向低温，在此情况下gradθ 为负值，为使从介质的全表面传导出去的热量为正值，故在等式右边加一负号。

式(9)为热传导方程，它用微分方程的形式来表达的各物理量在相邻空间和相邻时间的数值间的关系。

1.3 对流和辐射散热

一般情况下，热量从发热体表面散发到周围介质中区主要通过两个方式:一是辐射;二是借助于空气或者其他冷却介质的对流。在电机中，通常后者占主导地位。而计算由对流作用带走的热量时，为了方便，都采用牛顿散热定律

式中，q—热流强度(w/m2);α—为散热系统(w/m2·℃);θ1、θ2—固体和流体的温度。

2 计算以及分析

本文利用Ansys 对具有典型径向通风代表结构的电机进行建模、网格划分、计算求解和分析。

2.1 模型简化

为了给模型的网格划分提供一个简便的平台，需要根据以往建模和划分网格的经验对各个零部件进行合理的简化，合理的简化模型对有效划分网格和缩短后处理的计算时间有很大帮助。整机简化模型如图1 和图2 所示。

图1 Solidworks 整机模型

图2 Ansys 整机简化模型

2.2 网格划分

由于电机结构左右对称，在给出边界条件后为了减少计算量，本课题只对电机的左侧部分进行了建模，应用Ansys/APDL 语言建立方箱电机的三维模型并进行网格划分见图3。

图3 Ansys 简化整机模型

2.3 实例计算以及分析

2.3.1 方箱电机基本参数，见表1。

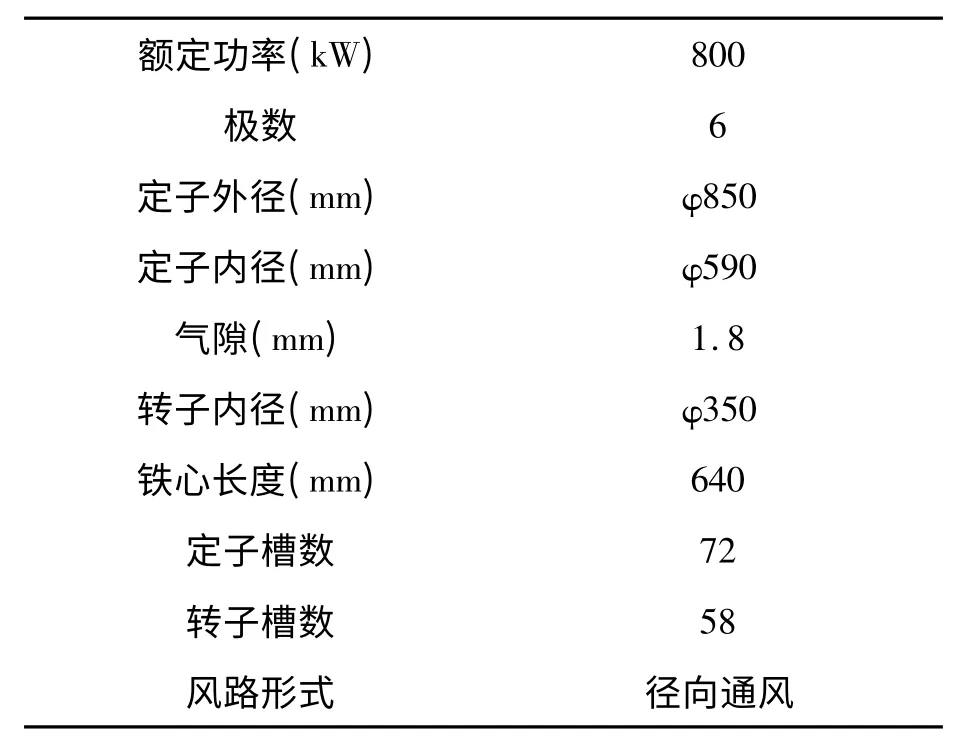
表1 方箱电机基本参数

2.3.2 电机的导热系数及生成率

通过方箱电机试验结果单所给出的损耗计算电机各部分的热生成率，即在单位时间内所产生的热量，电机各部分的热生成率和导热系数见表2和表3。

表2 方箱电机损耗及热生成率

表3 电机各部分导热系数

2.2.4 三维温度场的的计算

在电机的定转子绕组及定子铁心上施加损耗，并在机座外壳、机座通风道、气隙等施加散热系数等参数，计算电机的三维温度场，计算结果如图4-图9 所示。

图4 整机内侧温度场

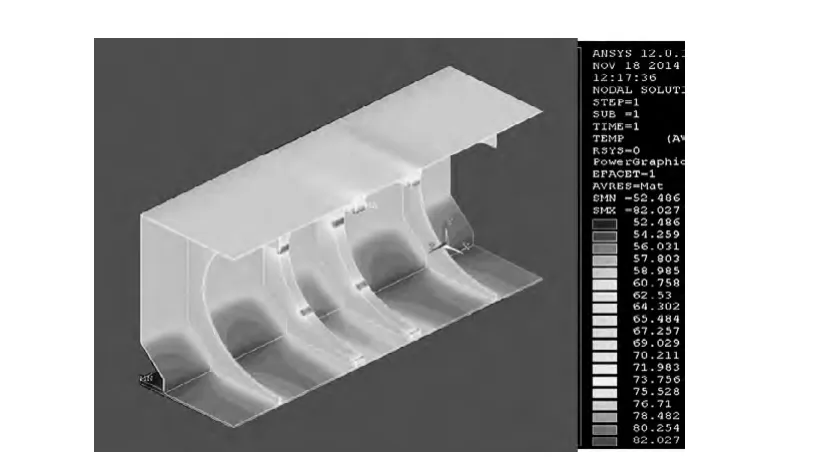
图5 机座侧温度场

图6 定子冲片内侧三维温度场

图7 定子冲片外侧三维温度场

图8 定子绕组内侧温度场

图9 定子绕组外侧温度场

2.2.5 结果分析

(1)从图3-图5 中可以看出，机座两侧板的温度在59℃(设置环境温度40℃)左右，根据以往电机型式试验的数据，电机两侧板温度在45℃～50℃(环境温度25℃)。侧板温升在20k 左右，此值与实际比较符合。

(2)根据方箱电机试验结果单，U1、U2、U3 埋在铁心端部，V1、V2、V3 埋在铁心中间部分，定子绕组的温度如表4 所示。

表4 定子绕组试验测量温度

在Ansys 的仿真结果中，定子绕组的端部温度为95℃，铁心中间的温度为101℃，与电机的实测温度约有10℃的误差，这是因为Ansys 仿真计算是基于理想的电机模型计算的，对电机的实际模型进行了相应的假设(如忽略了接触热阻等因素)。另外，电机的导热系数与实际值有一定的误差，计算散热系数所采用的风速只是近似的估计，并没有通过电机的流场分析，这些因素都很有可能导致上述温度误差的存在，但通过分析云图可以看出电机整体温度分布趋势是正确的，网格划分是合理的，结果能够起到指导和参考的作用。

(3)从图3-图9 中可以看出，越靠近铁心的中间部位，温度越高。因电机为径向通风，铁心两侧端部装有内风扇而且散热空间较大，风从两端进入铁心时，对铁心端部冷却相对较好，容易散热，而对于铁心中部来说，由于其散热空间有限，风阻大，通风情况相对铁心两侧端部较差，导致中间温度最高。因此，在实际的电机设计过程中，为了降低铁心中间温度，需在工艺允许的范围内，尽可能的增加铁心中部的通风道，同时减小通风道之间每段铁心的长度，通过改进的定、转子的铁心通风道的分配和段数，经实际试验温升都有明显下降，

3 结语

本文通过应用Ansys 对电机内部三维温度场进行建模和仿真分析，可知定转子靠近中间部分温度较高，因此在工艺允许的情况下，通过增加铁心中部的通风道，减小通风道之间每段铁心的长度来改善定转子铁心的通风散热，经过型式试验证明，这种改进有效的改善了电机的通风，降低了电机的温升，为合理优化内部结构提供了一定的理论基础。

［1］ 魏永田.电机内的热交换.北京:机械工业出版社，1998.

［2］ 胡俊辉，许承千.大中型异步电机通风的研究和计算.大型电机技术，1992.

［3］ 陈世坤.电机设计.北京:机械工业出版社，2000.