全波形积分式电流差动保护

于文斌，张国庆，郭志忠，宋 平，黄华炜

（1.哈尔滨工业大学电气工程学院，哈尔滨150001；2.国网上海市电力公司，上海200002）

电磁式电流互感器CT（current transformer）饱和是造成常规相量电流差动保护不正确的动作原因之一[1]。当引入差动回路的CT 出现严重饱和时，将产生较大的差流，在一定条件下就可能引起相量电流差动保护误动。采样值电流差动保护对每一时刻的采样值进行差动判别，在连续R 次判别中如有S 次满足判据，则输出动作信号。从CT 特性看，即使CT 饱和比较严重，在过零点附近也会有一段线性传变区，采样值电流差动保护通过合理地选择S、R 值来保证外部故障时不误动。因此，采样值电流差动保护能在一定程度上解决CT 饱和对保护带来的影响[2-4]。同时，采样值电流差动保护利用电流采样的瞬时值来实现基于相量的常规电流差动保护动作判据。其逻辑分析都是建立在纯正弦波形的基础上，一般假设故障时采样的电流仅由基波分量构成，即已滤去谐波分量、非周期分量等非工频成分[2-7]。如果存在衰减非周期分量，而CT 又不能准确传变衰减非周期分量，直接利用采样瞬时值进行判断，极有可能造成保护的误判[7]；但是如果对采样数据进行滤除衰减非周期分量的处理[8]，则必然影响采样值电流差动保护动作速度，而且也不符合采样值电流差动保护直接利用电流采样瞬时值判断的初衷。

近年来，光学电流互感器技术已趋于成熟，相应的产品在智能变电站中也得到了越来越多的应用[9-11]。光学电流互感器无磁饱和、无频带限制，在原理上能准确、迅捷地传变一次电流的全波形信息。光学电流互感器优良的测量性能在继电保护领域逐步得到应用[12-14]，将会促进保护新原理和新技术的研究。

本文提出的全波形积分式电流差动保护研究的动作判据是直接根据电流采样瞬时值进行积分计算来判断的，其动作时间不大于1/4 个工频周期，可以大大提高保护的动作速度。该全波形积分式差动保护是基于光学电流互感器的采样瞬时值，在分析保护特性时，充分考虑到系统衰减非周期分量的影响。采样初始时刻的随机性造成了全波形积分式电流差动保护判据存在一定的模糊区。为消除全波形积分式电流差动保护判据动作模糊区的影响，提出把常规相量电流差动保护作为辅助判据的复合差动保护方案，以提高保护的灵敏性。

1 保护判据

全波形积分式电流差动保护判据采用比率制动：取动作电流波形和制动电流波形的1/4 工频周期波形进行积分得到。对于微机保护，假设一个工频周期电流的采样点数是N，把连续N/4 个采样值动作电流id和制动电流iz分别相加，可得到判据为

式中：Sd为连续N/4 个采样值动作电流之和，Sd=为连续N/4 个采样值制动电流之和，为制动系数；I0为整定值。

以两端系统为例，其动作电流为

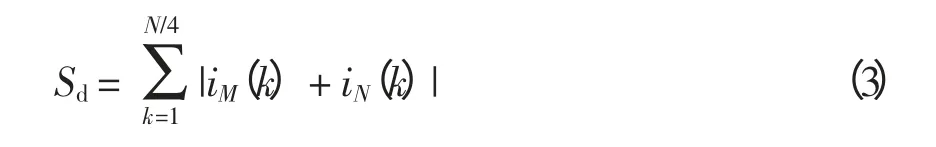
式中，iM、iN为引入差动回路的输入电流采样值。

制动电流同样可取和差制动、模值和制动及最大值制动。

（1）和差制动电流为

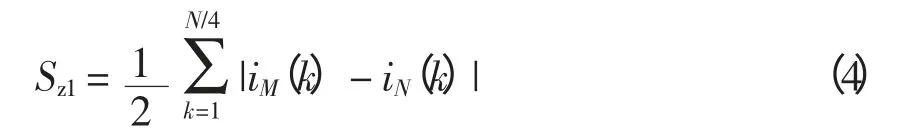
（2）模值和制动电流为

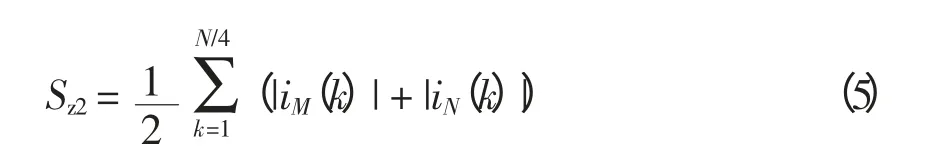
（3）最大值制动电流为

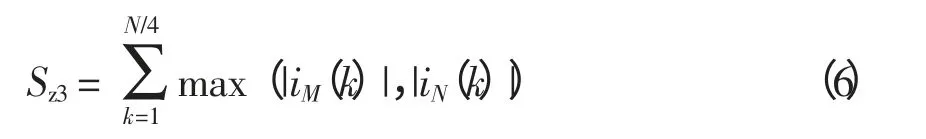
如果满足式（1）和式（2），保护就动作。本文取式（4）表示的和差制动电流进行分析和讨论。

图1 为仿真系统模型示意。规定母线指向线路方向为正方向。

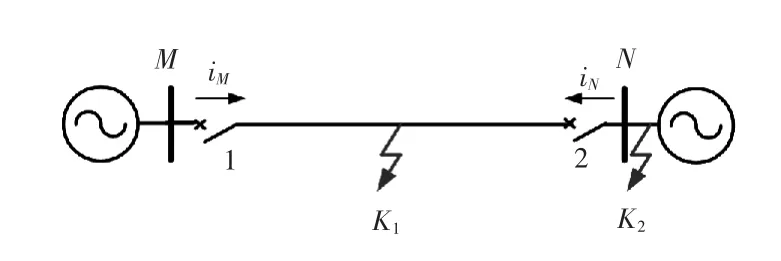
图1 仿真系统模型示意Fig.1 Sketch map of simulation system model

发生区外故障时，M 侧的故障电流表示为

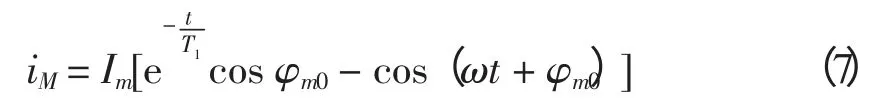
式中：Im为取决于短路条件的一次周期性电流的幅值；φm0为故障过渡过程开始瞬间（t=0）一次电流的初始相位角，0～90°；ω 为基波电流频率；T1为非周期分量的衰减时间常数，是一次回路中的电感与电阻的比值，取决于系统短路的地点和特性，可在百分之几到十分之几秒内变化。

N 侧的故障电流表示为

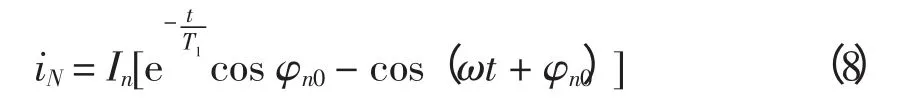
令ωt+φm0=θm，ωt+φn0=θn，φm0-φn0=180°+Δθ。则式（7）和式（8）可以分别表示为

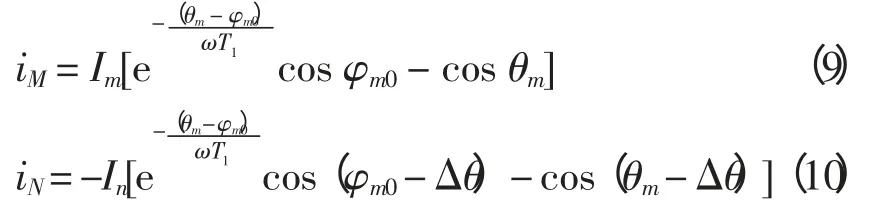
如无特殊说明，本文分析的采样值均基于光学电流互感器采样。

由于光学电流互感器能保真反映一次电流值、二次电流与一次电流之间存在的线性变比关系，所以在分析时，可以直接采用式（9）和式（10）来表示故障电流。

令Im= In，将式（9）和式（10）代入式（3）和式（4），可得制动比为

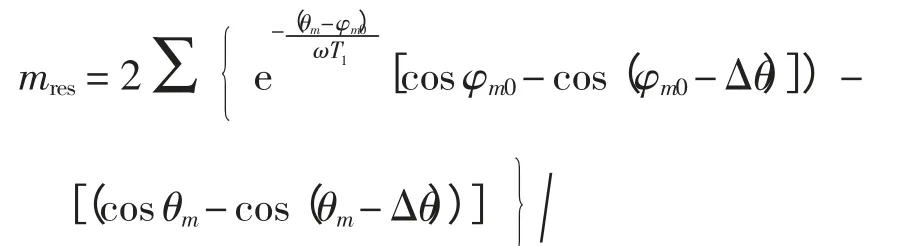
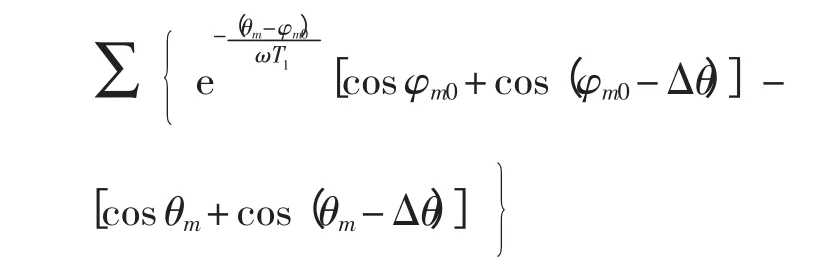
从式（11）可知，制动比随时间（即θm）或者说随电流采样点移动而变化，而且与两侧电流相位差和故障时刻初始相位有关。

2 保护特性分析

对于全波形积分式差动保护的动作电流Sd和制动电流Sz，可以采用梯形法则计算得到。采样率越高，计算精度越高。

动作电流Sd可以利用连续N/4 个两端电流采样值动作电流id（k）（k=1～N/4）求取，即

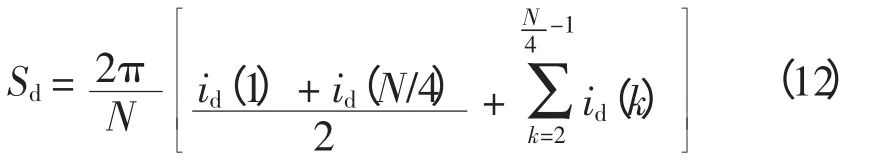
同理可得，制动电流的计算值为

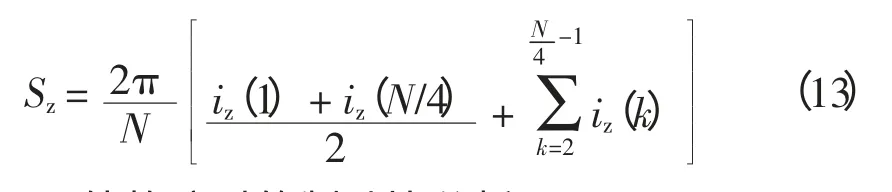
2.1 区外故障时的制动比分析

采用光学电流互感器时，一次电流转换到二次侧时几乎没有相位差，且基于光学互感器的继电保护装置本身产生的误差也可以忽略，如果不考虑线路分布电容的影响，线路两侧的故障电流几乎没有相位差。因此，考虑Δθ 的变化范围0～10°，取Δθ=10°进行分析。

取非周期分量的衰减时间常数T1为100 ms，根据故障初始时刻不同，取3 种情况讨论，即分别讨论φm0=90°、45°和0°时全波形积分式电流差动保护在区外故障时的制动特性。

图2 中（a）、（b）和（c）分别为故障初始相位φm0=90°、45°和0°时制动比随时间（即θm）或随电流采样点移动的变化曲线，制动比的最大值约为0.9。

由图可以看出，故障初始时刻对全波形积分式电流差动保护的制动比有影响，也即衰减非周期分量越大，制动比越小。光学电流互感器能准确传变系统衰减非周期分量有利于提高全波形积分式电流差动保护的制动效果。

考虑上述条件，取制动系数K=1.2。

2.2 区内故障时的动作特性分析

区内故障时，两端故障电流可以分别表示为

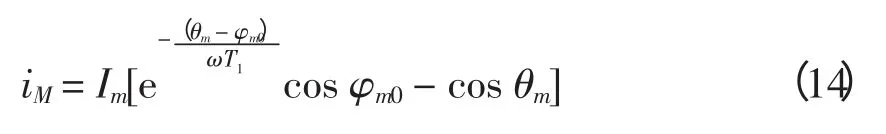
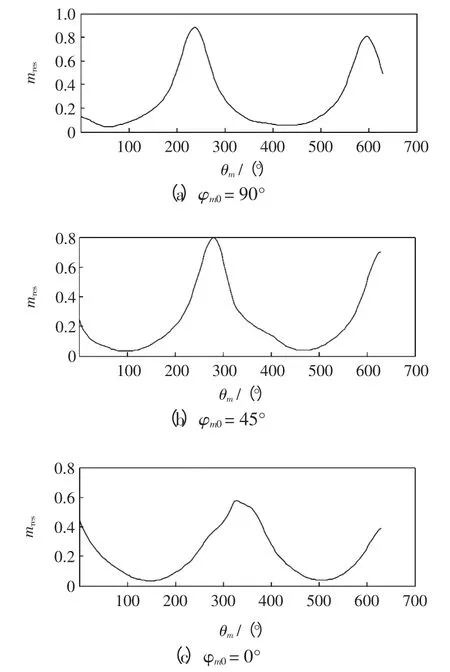
图2 区外故障时的制动比曲线Fig.2 Restraint ratio curves with external fault

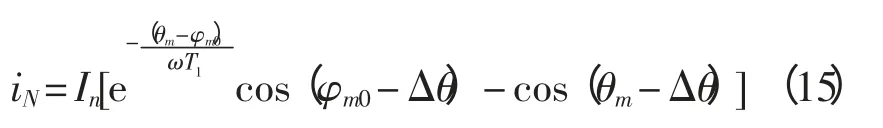
考虑最不利情况下的保护范围内部故障，两端故障电流相位差Δθ=70°，主要是由短路前两侧系统电动势引起的相位差。

取非周期分量的衰减时间常数为100 ms，分别讨论φm0=90°、45°和0°时全波形积分式电流差动保护在区内故障时的动作特性，特性曲线如图3所示。

由图3 可以看出，在最不利的情况下发生保护范围内部故障，即两端故障电流相位差Δθ=70°时，全波形积分式电流差动保护的最小制动比为0.5。

2.3 动作模糊区分析

根据上述仿真分析结果，由于全波形积分式差动保护利用1/4 工频周期的采样值数据的积分求取判据，采样初始时刻的随机性造成了式（2）描述的保护判据存在一定的动作模糊区，此模糊区范围为K=[0.5，0.9]。当保护制动系数设置值大于模糊区上限时，保护可能会发生区内拒动；当保护制动系数设置值小于模糊区下限时，保护可能会发生区外误动。

为了消除该保护判据动作模糊区的影响，必须采取辅助判据的方法构成复合保护方案。

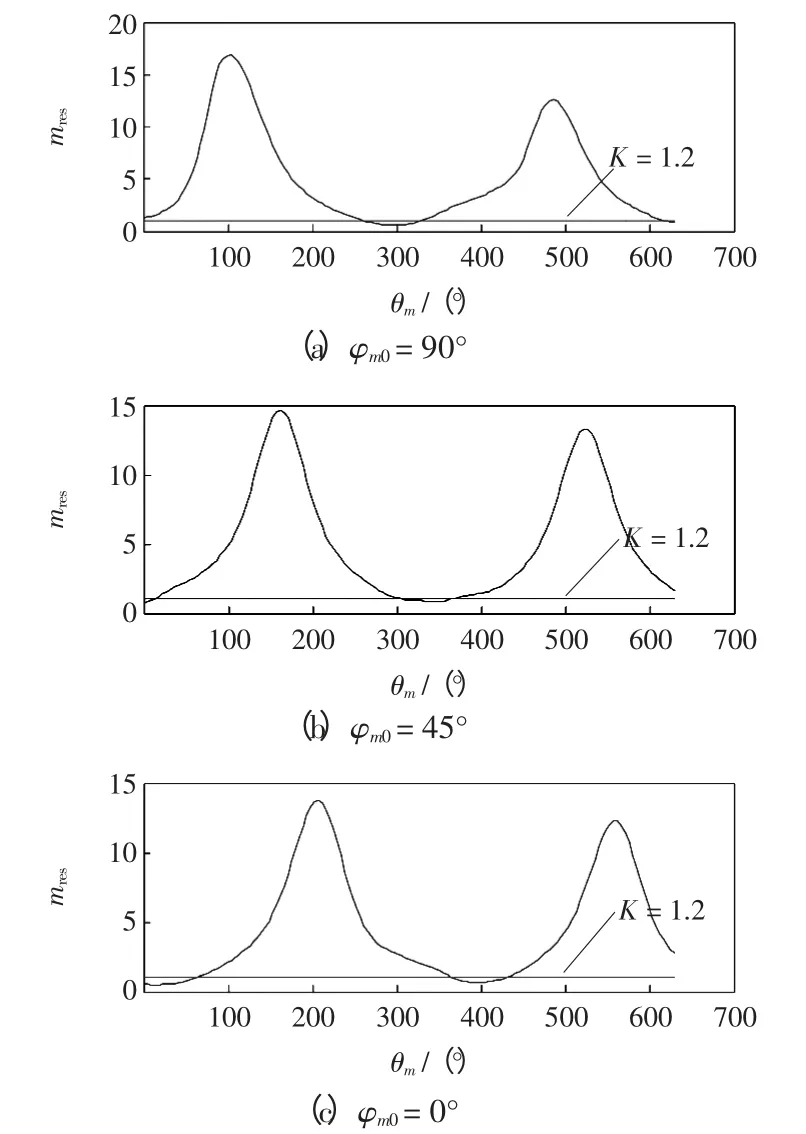
图3 区内故障时的制动比曲线Fig.3 Restraint ratio curves with internal fault

3 复合差动保护方案

结合相量电流差动保护和全波形积分式电流差动保护的性能特点，提出复合差动保护方案，充分利用两种差动保护方法的优点，使其相互协调配合，以达到更好的综合保护性能。复合差动保护方案如图4 所示。

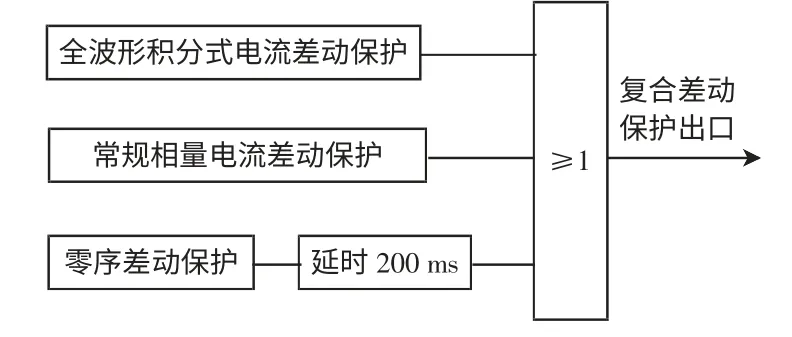
图4 复合差动保护方案Fig.4 Composite differential protection scheme

为消除全波形积分式电流差动保护判据动作模糊区的影响，复合差动保护方案把常规的相量电流差动保护作为辅助判据：先投入全波形积分式电流差动保护，如果保护不动作，则投入常规的相量电流差动保护。因此，对于全波形积分式电流差动保护，可以通过设定式（2）中K 的值，使得式（2）的判据实现“可以拒动，但一定不误动”，即只有制动比大于保护动作模糊区的上限值时，全波形积分式电流差动保护才动作；而制动比小于动作模糊区上限时，全波形积分式电流差动保护可靠不动作；处于动作模糊区时，由相量电流差动保护决定是否动作。

3.1 速动性分析

由于复合差动保护方案中引入了全波形积分式电流差动保护，使保护动作速度得到了较大提高。全波形积分式电流差动保护在1/4 工频周期内即能做出判断，相对于利用全周傅里叶算法的常规相量电流差动保护，保护速度有了明显的提高。

3.2 灵敏性分析

全波形积分式电流差动保护利用1/4 工频周期的采样值数据进行积分求取判据，采样初始时刻的随机性造成了动作模糊区，复合差动保护方案中利用常规相量电流差动来弥补这一不足。基于傅氏算法的相量电流差动保护动作特性不受采样初始时刻的影响，长期以来的运行经验表明，能可靠地反映各种内部故障。复合差动保护方案中还采用了零序差动保护作为后备保护，延时200 ms躲过故障暂态后动作，能进一步提高高阻接地故障时保护的灵敏度。

4 结语

本文提出了基于光学电流互感器的电流采样瞬时值的全波形积分式电流差动保护，并对其原理和动作特性进行了仿真分析，从理论上论证了该保护判据的可行性。将常规相量差动保护作为全波形积分式差动保护的辅助判据，给出了复合差动保护的方案。但是具体到实际的应用，还需要做不少的实际算例验证工作。后续研究将围绕全波形差动保护算法的优化开展，通过对该算法特性的深入分析，结合实际工程应用，进一步优化复合差动保护方案。

[1]胡晓光，王哲，于文斌（Hu Xiaoguang，Wang Zhe，Yu Wenbin）. 电流互感器暂态过程的仿真与分析（The transient simulation and analysis of current transformers）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2001，13（4）：12-15.

[2]陈德树，马天皓，刘沛，等（Chen Deshu，Ma Tianhao，Liu Pei，et al）.采样值电流差动微机保护的一些问题（Problems in realization of microcomputer based differential current protection by sampled values）[J]. 电力自动化设备（Electric Power Automation Equipment），1996，16（4）：3-8.

[3]陈德树，尹项根，张哲（Chen Deshu，Yin Xianggen，Zhang Zhe）.再谈采样值差动保护的一些问题（On problems about sampling value differential protection）[J].电力自动化设备（Electric Power Automation Equipment），2000，20（4）：1-3.

[4]张兆云，刘宏君，岳蔚，等（Zhang Zhaoyun，Liu Hongjun，Yue Wei，et al）.采样值差动在线路差动保护中的应用（Sampled values based differential protection for line differential protection）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（12）：76-79.

[5]袁荣湘，陈德树，马天皓，等（Yuan Rongxiang，Chen Deshu，Ma Tianhao，et al）.采样值电流差动保护原理的研究（Study on the principle of current differential protection based on sampled values）[J].电力自动化设备（Electric Power Automation Equipment），2000，20（1）：1-3.

[6]杨经超，尹项根，陈德树，等（Yang Jingchao，Yin Xianggen，Chen Deshu，et al）.采样值差动保护动作特性的研究（Study on the operating characteristic of sampled value differential protection）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（9）：71-77.

[7]林湘宁，何战虎，刘世明，等（Lin Xiangning，He Zhanhu，Liu Shiming，et al）.电流采样值差动保护若干问题的探讨（Discussion on some aspects of sampling value differential current protection）[J].电力系统自动化（Automation of Electric Power Systems），2001，35（19）：27-33.

[8]陈海滨，王增平，徐岩，等（Chen Haibin，Wang Zengping，Xu Yan，et al）.校正交流采样数据滤除非周期分量的实用算法（Practical algorithm to eliminate non-periodic components from AC sampling data）[J].电力科学与工程（Electric Power Science and Engineering），2007，23（2）：5-8.

[9]刘孝先，曾清，邹晓莉，等（Liu Xiaoxian，Zeng Qing，Zou Xiaoli，et al）.电子式互感器的应用（Application of electronic transformer）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（1）：133-137.

[10]郭志忠（Guo Zhizhong）. 电子式互感器评述（Review of electronic instrument transformers）[J]. 电力系统保护与控制（Power System Protection and Control），2008，36（15）：1-5.

[11]王红星，张国庆，郭志忠，等（Wang Hongxing，Zhang Guoqing，Guo Zhizhong，et al）.电子式互感器及其在数字化变电站中应用（Electronic transformer and its application in digital substations）[J].电力自动化设备（Electric Power Automation Equipment），2009，29（9）：115-120.

[12]刘青，王增平，徐岩，等（Liu Qing，Wang Zengping，Xu Yan，et al）.光学电流互感器对继电保护系统的影响研究（Research on the influence of optical current transducer on protective relaying system）[J].电网技术（Power System Technology），2005，29（1）：11-14，29.

[13]滕林，刘万顺，李贵存（Teng Lin，Liu Wanshun，Li Guicun）.光学电流传感器及其在继电保护中的应用（Optical current transducer and its application in protective relaying）[J].电网技术（Power System Technology），2002，26（1）：31-33，42.

[14]顾黄晶，张沛超（Gu Huangjing，Zhang Peichao）.光学电流互感器对线路差动保护的影响（Influence of optical current transducer on line differential protection）[J].电力自动化设备（ElectricPowerAutomationEquipment），2007，27（5）：61-64.