运用多元回归分析法估算身高和体重
甘霖
(中国刑警学院 辽宁 沈阳 110035)
运用多元回归分析法估算身高和体重
甘霖
(中国刑警学院 辽宁 沈阳 110035)
利用足迹分析犯罪嫌疑人的身高和体重一直是足迹学中较为重要的研究课题。为解决运用一元回归方法来分析犯罪嫌疑人的身高和体重具有一定局限性和不准确性的问题,在一元回归分析的基础上,收集大量的赤足足迹样本,然后运用多元回归分析法来估算犯罪嫌疑人的身高和体重。通过实验得出的多元回归方程不仅能够有效利用多个足迹特征长度测量值,而且提高了分析结果的准确性。
赤足 多元回归分析 身高 体重
利用案发现场的足迹来推测犯罪嫌疑人的身高、体重是公安足迹勘验工作的主要任务之一。多数是根据足迹的部分特征长度测量值来实现的,准确性较高。
本文运用多元回归分析的方法,利用足迹的部分特征测量值来实现对犯罪嫌疑人身高、体重的推测,本文运用多元回归分析的方法来研究足迹样本。
1 多元回归分析法
回归分析是运用统计学的方法构建数学模型,从而得到因变量与自变量之间的关系,(建立模型)利用得到的数学模型和已知的自变量来估算或推测出因变量的值。多元回归分析就是指建立的数学模型中包涵有两个或者两个以上的自变量。多元回归的方程式为:
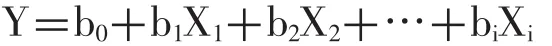
其主要目的研究足迹各个特征测量值与人的身高、体重的关系,以及得出运用哪些测量值来分析人的身高、体重最为准确的结论。
2 样本选取
选取中国刑事警察学院500名男性学员(20~30岁)的赤足足迹捺印样本。除此之外,这500名学员的出生地、居住地均较分散,从而提高了实验结果的准确性。参与样本捺印的500名学员均被要求在正常行走的状态下进行捺印,选取效果较好的捺印样本作为实验用样本。
3 测量方法
选定左脚赤足足迹跟后缘最突点,分别测量左脚足迹跟后缘最突点到左脚各个脚趾的前缘最突点的距离,从拇趾头到第五趾头与足迹跟后缘最突点的距离分别用LT1、LT2、LT3、LT4、LT5表示;再选定左脚赤足足迹的跖、跟内缘突点和外缘突点,分别测量足迹跖内、外缘突点的距离和足迹跟内、外缘突点的距离,分别用LFBB、LFBH表示(如图所示)。右脚赤足足迹测量值的测量方法与左脚相同,其分别表示为RT1、RT2、RT3、RT4、RT5、RFBB和RFBH。

图 测量方法图
本实验所用的是SPSS(Statistical Program for Social Sciences)19.0统计分析软件。在对数据进行测量过后,将收集到的500名学员的左、右脚赤足足迹的测量值录入到SPSS统计分析系统中,然后对数据进行回归分析,从而得出左脚7个测量值与右脚7个测量值,共计14个测量值与身高和体重之间的相关性,以及这14个测量值相互之间的相关性。
4 结果分析
4.1 相关性
通过SPSS系统的回归分析,首先得到了所有自变量与因变量的“均值”和“个数”(实际算入到统计系统的变量的个数)。其中关于身高和体重的分析系统中实际选入的各变量的个数分别为500和499。然后可以看到表1和表2所示的因变量与自变量以及自变量之间的Pearson相关性。在这里表1和表2所要表示的是各个自变量与“身高”和“体重”这两个因变量的相关性大小,以及各个自变量之间是否存在着共线性问题。从表1中可以看出,“身高”与“LT1”、“LT2”、“LT3”、“LT4”、“LT5”、“RT1”、“RT2”、“RT3”、“RT4”、“RT5”的相关性均较高,相关系数在0.553~0.599(p<0.01)之间;而“身高”与“LFBB”、“LFBH”、“RFBB”、“RFBH”的相关系数在0.303~0.321(p<0.01)之间,处于相对较低的水平;从表2中可以看出,“体重”与“RFBB”、“LT2”、“RT1”的相关性相对其它的自变量较高,相关系数分别为0.381(p<0.01)、0.341(p<0.01)、0.348(p<0.01)。而“LT1”、“LT2”、“LT3”、“LT4”、“LT5”、“RT1”、“RT2”、“RT3”、“RT4”、“RT5”这10个自变量之间的相关系数在表1和表2中都处于0.792~0.965的范围之内,相关程度较高;并且“LFBB”与“RFBB”、“LFBH”与“RFBH”之间的相关系数分别为0.812与0.788,相关程度同样较高,由此可以说明自变量中存在着共线性问题。如果不考虑这一问题,把所有自变量全部选入到最后的回归模型中可能会导致预测结果的不准确,于是可以推测出在最后建立的数学模型中可能根据相关性的大小只选入较为重要的变量投入到多元回归分析之中。
4.2 模型分析
本实验中由于自变量之间存在着共线性问题,于是在使用回归分析法时,回归模型会根据各自变量对因变量预测能力的高低,而依次将自变量逐个地选入到回归模型中。当自变量的回归系数没有达到显著水平时,该自变量就会被排除在回归模型之外,从而得到了表3和表4所示的模型汇总。如表3和表4所示,其中的R表示相关系数,R越接近于1,表明自变量与因变量之间的相关性越强;而相关指数R2越接近于1,同样说明自变量与因变量之间的相关性越强,于是我们可以选择R2较大的作为回归模型,F改变的值表示的是回归方程的显著性检验,即对模型中被解释变量与所有解释变量之间线性关系在总体上是否显著做出判断。在表3中所呈现的模型1、模型2和模型3,以及表4中呈现的模型1和模型2的自变量的回归系数均达到了显著水平。如表3所示,模型1的自变量“RT1”对因变量“身高”的解释能力为35.8%,此解释力已经达到了统计上的显著水平(F改变=278.205,p=0.00<0.01);模型2中加入了自变量“RT4”,这两个自变量“RT1”、“RT4”对因变量“身高”的解释能力为38.0%,排除自变量“RT1”的影响,自变量“RT4”对因变量“身高”的解释力为2.2%,此解释力已经达到了统计上的显著水平(F改变=18.007,p=0.00<0.01);模型3中加入自变量“LT1”,三个自变量“RT1”、“RT4”、“LT1”对因变量“身高”的解释能力为38.7%,排除自变量“RT1”、“RT4”的影响,自变量“LT1”对因变量的解释力为0.7%,此解释力并没有达到统计上的显著水平(F改变=5.356,p=0.02>0.01),但是由于三个回归模型的F值分别为278.206(p<0.01)、152.857(p<0.01)、104.583(p<0.01),均达到了显著水平,所以并不影响自变量“LT1”被选入到回归模型中。表中Durbin-Watson检验的值为1.802,说明该回归模型中共线性问题不严重(DW统计量数值越接近2时,表示相关系数越接近0,各自变量间不存在自相关)。
如表4所示,模型1的自变量“RFBB”对因变量“体重”的解释能力为14.5%,此解释力已经达到了统计上的显著水平(F改变=84.605,p=0.00<0.01);模型2中加入了自变量“LT2”,这两个自变量“RFBB”、“LT2”对因变量“体重”的解释能力为18.2%,排除自变量“RFBB”的影响,自变量“LT2”对因变量“体重”的解释力为3.7%,此解释力已经达到了统计上的显著水平(F改变=22.185,p=0.00<0.01),并且模型1和模型2的F值分别为84.605(p<0.01)、55.198(p<0.01),均达到了显著水平。Durbin-Watson检验的值为1.826,说明该回归模型中共线性问题不严重。
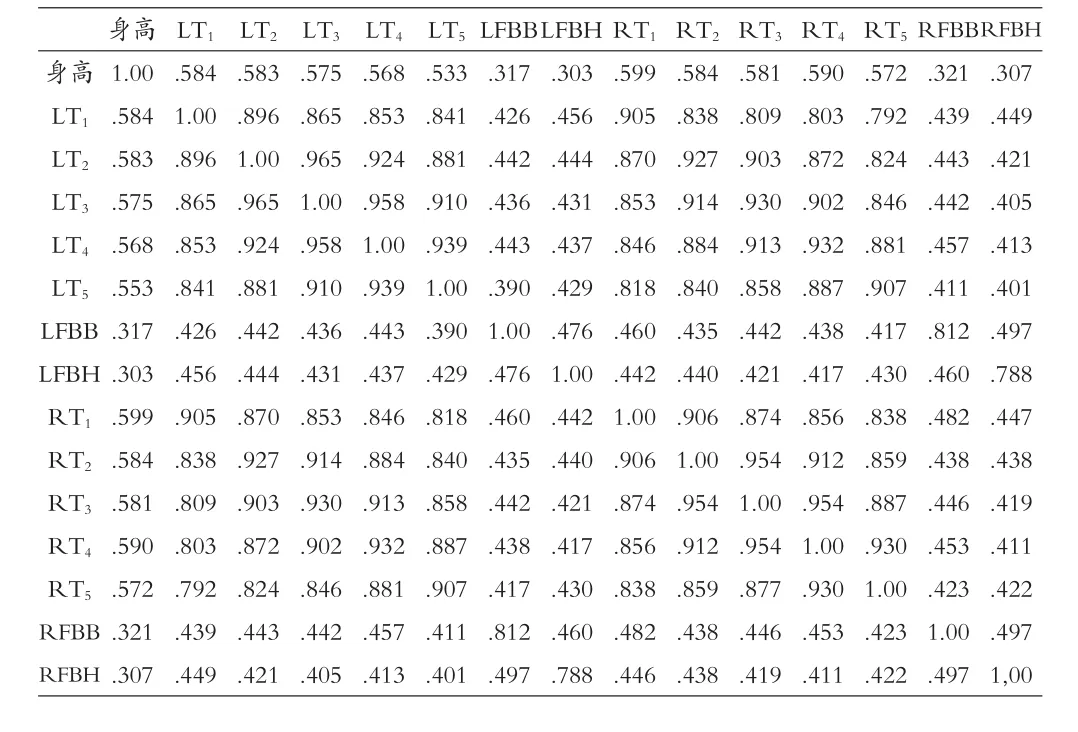
表1 Pearson相关性(身高)
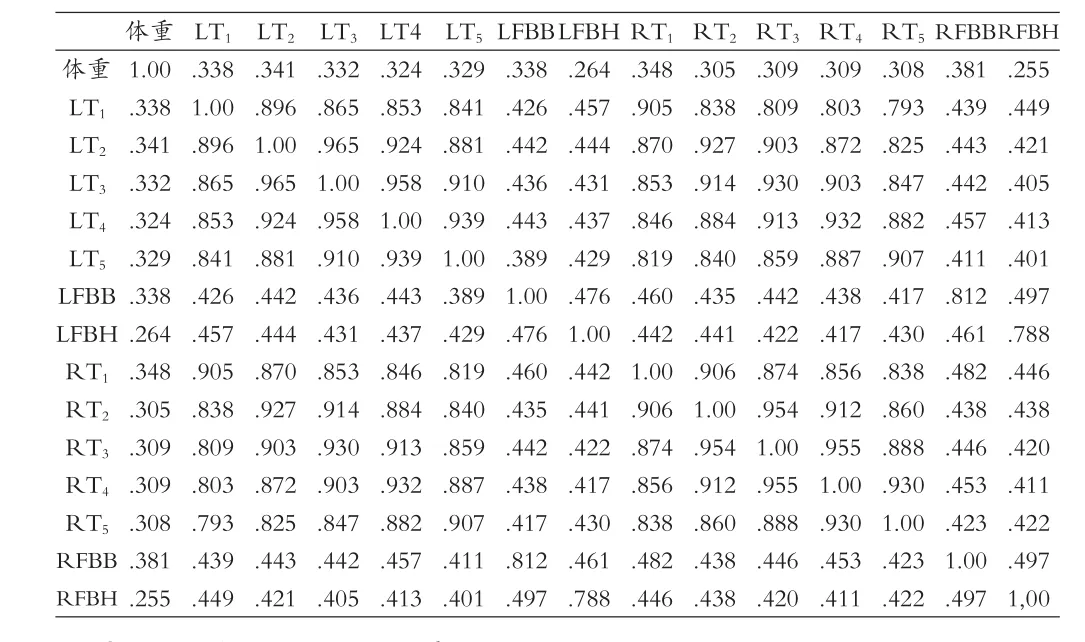
表2 Pearson相关性(体重)
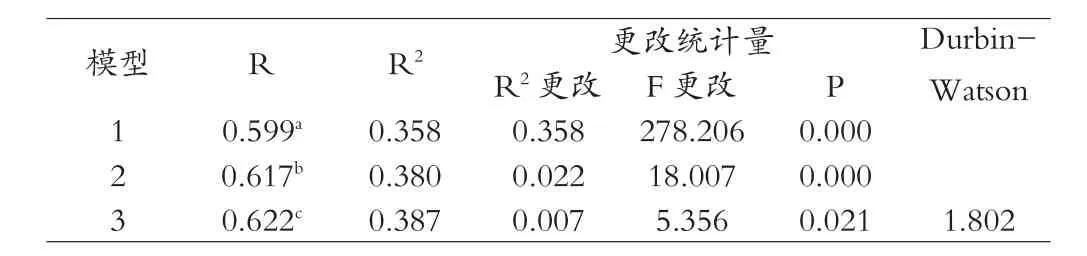
表3 模型汇总(身高)
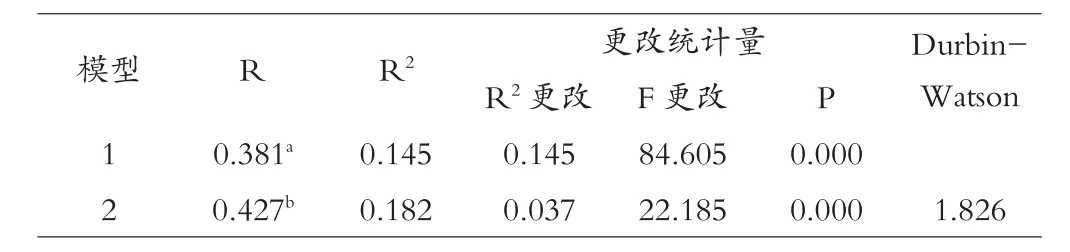
表4 模型汇总(体重)
4.3 选取模型
通过对因变量和选入模型的自变量的回归分析,得出了表5和表6所示的回归模型的回归系数及回归系数的显著性。其中还包含了容差和VIF(方差膨胀系数),这两项内容都是反映自变量间共线性问题的数值,容差值越接近0表示变量间存在多元共线性问题,同时VIF值大于10时,也表示自变量间存在多元共线性问题。如表5所示,模型1为一元回归方程,模型2和模型3为多元回归方程,由表3可知模型1的解释能力最低;而在模型2与模型3相比较的情况下,虽然模型3的解释能力比模型2要高出0.7%,但是模型2的显著性更强(p<0.01),所以在适用性上将优先选择模型2,该模型中自变量“RT1”、“RT4”的回归系数分别为1.582、1.403。如表6所示,模型1为一元回归方程,模型2为多元回归方程。同样由表4可知模型2的解释能力要高于模型1,所以在实际案件的运用中将优先选择模型2,该模型中自变量“RFBB”和“LT2”的回归系数分别为5.174、1.645,且显著性较高(p<0.01)。

表5 系数a(身高)

表6 系数b(体重)
5 讨论
在办案实践中,可以根据在犯罪现场中提取到的足迹,利用上述建立的多元回归模型来推测出犯罪嫌疑人的身高和体重。但该多元回归模型在实际应用中,需要注意以下问题:
(1)本实验选取的样本捺印人员年龄均在20~30岁之间,性别均为男性,并且人的身高在成年以后基本不会再随着年龄的增长而有较大幅度的变化,故对于多数的案件都是适用的。但是,在特殊情况下,例如案件中出现青少年犯罪时,则需要根据具体的情况加以分析。
(2)本次多元回归分析是建立在赤足足迹的基础上。在实际案件的应用中,现场足迹的类型、形成物质以及形态都是多样的,对于赤足或穿袜足迹,则可以直接运用建立的模型来推测身高和体重;对于穿鞋足迹,则需要在进行运算之前对现场穿鞋足迹的长度减去一个对应鞋种的鞋边系数,然后再用模型进行推测。对于现场上出现的残缺足迹、雪地上的足迹、承痕客体容易发生变形的足迹等,应视具体情况做出具体分析。
(3)本次实验的取样数量为500,且取样范围相对较分散,所以,实验结果可能会因为数据量较小而产生一定的误差。
[1]Irene Atef Fawzy,Nashwa Nabil Kamal.Statu re and Body W eight Estimation from Various Footprin t Measurements Among Egyptian Population[J].Forensic Sic,2010,55(4):884-888.
[2]Derya Atam turk,Izzet Duyar.Age-Related Factors in the Relationship between Foot Measurements and Living Stature and Body Weight[J].Forensic Sci,2008,53(6):296-1300.
(责任编辑:孟凡骞)
D 918.3
A
2095-7939(2015)04-0051-03
2015-05-06
甘霖(1996-),女,河南信阳人,中国刑警学院研究生,主要从事足迹检验鉴定研究。

