一种小型单兵巡飞弹的气动外形设计
陶福兴,张 恒,李 杰
(西北工业大学航空学院,西安 710072)
一种小型单兵巡飞弹的气动外形设计
陶福兴,张 恒,李 杰
(西北工业大学航空学院,西安 710072)
文中针对一种适合于单兵使用的小型攻击型巡飞弹进行气动外形设计和分析。在考虑低雷诺数效应和封装特性要求的前提下确定了巡飞弹设计基本指标和串列翼气动布局形式,完成了气动外形设计工作;对所构造的巡飞弹气动外形在设计和非设计条件下的气动力进行了数值模拟。计算结果表明所设计的巡飞弹构型满足设计指标要求,具备良好的飞行性能。设计所得的相关结论可为工程应用提供一定参考。
巡飞弹;低雷诺数;串列翼;数值模拟
0 引言
巡飞弹(loitering munition)是一种可利用多种武器平台投放,在目标区上方巡弋飞行,以执行精确打击、侦察与毁伤评估、通信中继、目标指示、空中预警等多种作战任务的新型精确制导武器。
根据实际战术用途,巡飞弹可分为攻击型和侦察型两大类。侦察型巡飞弹携带侦察及通信器材,可执行搜索、侦察、监视、中继通信以及毁伤评估等任务。攻击型巡飞弹除具备一定侦搜能力之外,还携带有战斗部,可对作战目标进行精确打击[1]。主要战术技术性能指标为巡飞时间和作战距离:巡飞时间一般为15 min~12 h,作战距离为10~100 km;巡飞高度为100~1000 m,弹道段飞行速度一般为30~100 m/s。
20世纪90年代以来,美国、英国、俄罗斯和以色列等国在攻击型巡飞弹领域开展了大量的研究工作。其中美国“弹簧刀”巡飞弹属于一类比较有特色的单兵攻击型巡飞弹,具有侦察打击一体化能力;最大航程可达40 km,持续飞行时间50 min,能够人在回路中控制精确攻击目标。同时具备成本较低、方便单兵使用和携带等优点,已正式步入作战使用阶段[2]。
对于单兵携带的小型巡飞弹而言,其飞行的低雷诺数效应较为显著,并且在外形尺寸大小和动力装置性能的严格限制下,要求尽量较长的航时和航程,对相关气动设计问题构成了一定挑战。
针对巡飞弹气动设计问题,史文东[3]等基于气动估算和Euler方程数值计算相结合的方法,分析了巡飞弹的基本气动特性;魏明[4]等利用RANS数值模拟手段,探讨了充气翼巡飞弹的低雷诺数绕流情况;纪秀玲[5]等利用风洞试验研究了非圆截面巡飞弹的气动特性,并就巡飞弹高升力弹翼的设计原则进行了探讨和总结。
1 巡飞弹气动外形设计
文中所要设计的是一种适合于单兵携带和使用的小型攻击型巡飞弹,飞行速度和高度较低。设计目标是在低雷诺数和封装特性等因素的限制下,使构型具备较长的航程和航时。
结合国外相似类型巡飞弹的设计经验,给定巡飞弹气动设计主要指标如下:
a)干净构型在巡航飞行时升阻比大于8;
b)在飞行过程中纵向稳定裕度大于5%;
c)弹翼折叠后不超出弹身最大轮廓线。
对于所设计的巡飞弹而言,由于其应在低雷诺数下提供足够的升力,并具备良好的升阻特性,应当使用较大展弦比的弹翼,但由于弹翼在折叠状态下必须完全收纳进入弹身,并且对于薄翼而言,若展弦比过大则弹翼的刚度要求无法满足。限于弹身尺寸及封装要求,采用串列翼气动布局形式[6-7]。
串列翼布局(tandem wing configuration)属于鸭式布局的一种,其前翼可以看作面积加大、展弦比增加的鸭翼,但鸭翼主要用于产生配平和俯仰控制力矩,升力贡献不大,而串列翼布局前翼除配平后翼升力外,自身也产生相当部分的升力。由于串列翼布局升力为前后翼分别产生,重心居于两者之间,故易于在产生升力的同时维持全机力矩平衡,避免配平阻力产生。
1.1 弹翼设计
弹翼是巡飞弹的主要升力面,对其飞行性能和飞行品质有着重要的影响。考虑到所设计巡飞弹的低雷诺数特征,其弹翼设计的基本要求为:保证在巡航升力系数条件下较高的升阻比,巡航状态下弹翼各剖面分离流强度尽可能低;在对应失速状态的大攻角条件下,保证具有可接受的纵向安定性。
由于大展弦比将造成弹翼提前失速,则对于串列翼布局飞行器而言,前翼展弦比应大于后翼,使其在后翼之前失速;从而使巡飞弹在风切变等情况引起失速时,能够维持纵向静稳定性并改出失速状态。若后翼先失速,则因前翼残余升力位于重心前方,则飞行器的上仰失速趋势是无法抑制的。
选取弹翼基本翼型为NACA2405,基于目标压力分布反设计思路,运用Takanashi迭代程序完成翼型改进优化设计[8]。
1.2 尾翼设计
由于巡飞弹垂尾在封装状态下也应收纳在弹身最大横截面轮廓线以内,同时鉴于垂尾面积应当充分大以确保足够的横航向稳定性,采用倾斜双垂尾布局形式。
1.3 几何外形设计结果
根据各部件气动外形设计结果,建立如图1所示的巡飞弹几何外形。

图1 巡飞弹几何外形
2 数值求解方法及算例验证
基于有限体积法求解三维雷诺平均N-S方程(RANS)进行数值计算。采用二阶迎风格式进行无粘项离散,中心差分格式进行粘性项离散。
由于所研究的低雷诺数问题层流效应比较明显,因此应当选取计及流动转捩的湍流模型。基于压力脉动是导致来流扰动进入边界层的主要原因这一理论,Walters、Leylek及Volino[9-10]提出了基于局部变量的k-kl-ω转捩模型。该转捩模型为包含湍流动能kT、层流动能kL和耗散率ω的三输运方程:
(1)
(2)
k-kl-ω转捩模型在低雷诺数流动时针对湍流动能和层流动能方程分别求解,同时考虑了旁路转捩和自然转捩,当流动雷诺数较低时,通用性和准确性都较高。
为验证数值方法对低雷诺数流动的计算精度,针对典型低雷诺数翼型Eppler387开展计算分析。
图2和图3分别给出了Ma=0.08,Re=2E+5时计算所得翼型气动特性曲线及表面压力分布与实验值的对比情况。此处实验值取自参考文献[11]中NASA兰利低湍流度风洞对该翼型进行的低雷诺数实验[11]。
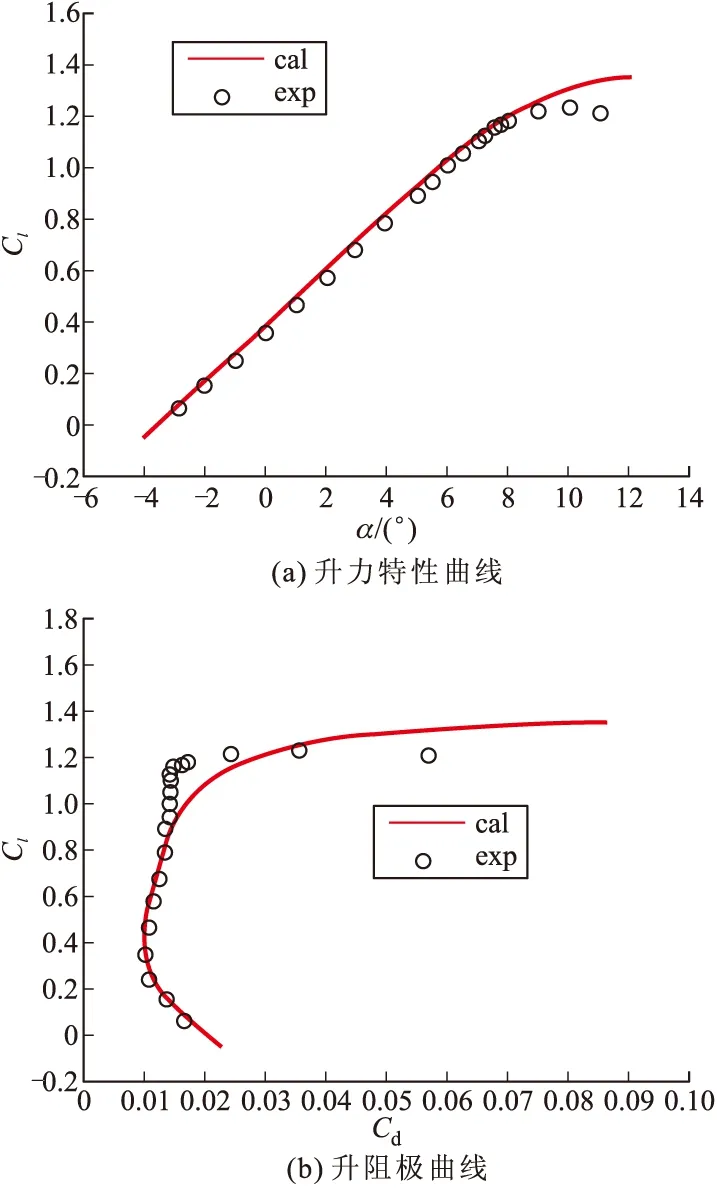
图2 计算所得翼型气动特性曲线与实验值对比

图3 计算所得翼型表面压力分布与实验值对比
由图2和图3可知:计算所得的翼型气动力系数变化曲线与实验值相符合,翼型表面压力分布亦与实验值吻合良好,能够反映因层流分离泡存在而产生的上表面压力平台。
该算例证明通过运用k-kl-ω转捩模型,数值模拟方法能够较好的描述低雷诺数下的流动形态和气动力,具备较高的计算可靠性。
3 巡飞弹气动性能分析
针对所设计的巡飞弹干净构型,对构型取不同攻角时典型巡航马赫数和雷诺数下的纵向气动特性进行了计算和分析。表1和表2给出了设计方案的基本几何参数和巡航状态计算参数。飞行重量参照相关文献数据,按1.4 kg计算。

表1 巡飞弹几何参数参数参数值Sref/m20.042c/m0.04弹长/m0.36重心相对位置/%41.67表2 巡飞弹计算参数参数参数值海拔/km2.5飞行高度/m100Ma0.1Re7.5E+4
3.1 巡航状态气动性能计算
对攻角α=-15°、-13°、-11°、-10°、-8°、-5°、-3°、0°、3°、5°、8°、10°、11°、13°共计15个状态下的三维构型升力系数CL、阻力系数CD、俯仰力矩系数CM展开计算。升力特性、升阻特性、力矩特性曲线如图4所示。

图4 巡飞弹气动特性曲线


图5和图6分别给出了典型巡航攻角下巡飞弹前后翼展向等百分比位置压力分布情况。可见由于前翼尾流产生的下洗流动影响遍及整个后方流场;故即使后翼位置未直接处于前翼尾流区域内,在构型同一攻角下后翼实际来流攻角仍小于前翼,使其压力分布形态总是较前翼有所推迟;且随着前翼攻角的增加,下洗效应逐渐显著。此时前翼气动效率应高于后翼。
3.2 非巡航状态气动性能计算
对于构型在非巡航速度状态下的气动特性,分别选取速度V=25m/s、30m/s、40m/s、45m/s四个状态在攻角α=5°的情况下进行计算。计算结果见图7所示。
由图7可知,在所给飞行条件下,随着飞行速度不断上升,飞行雷诺数逐渐增加,低雷诺数效应影响减弱,构型升阻特性逐渐改善,气动效率提高;构型升力系数随速度变化基本呈线性增长趋势,但阻力系数的下降过程显示出了一定的非线性特征。注意在构型纵向静稳定的前提下,虽然升力系数随飞行速度而增加,但低头力矩大小反而减小,与单独升力面情形恰好相反。这是由于串列翼布局当中前翼气动效率较高,升力系数随飞行速度变化的增量相对后翼也较高,使得升力作用点前移,总体呈现低头力矩减小趋势。
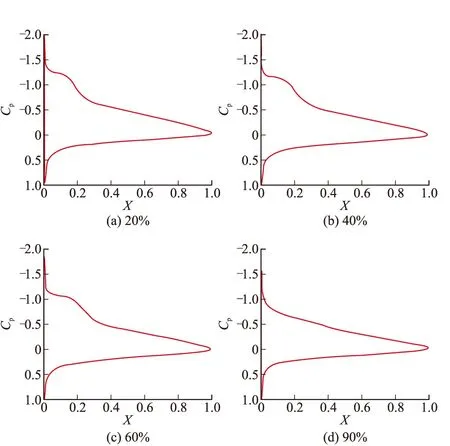
图5 构型前翼展向不同站位压力曲线,α=5°

图6 构型后翼展向不同站位压力曲线,α=5°
3.3 气动性能分析总结
巡航状态计算结果表明,所设计的巡飞弹在满足结构和封装等限制条件的前提下,对于低雷诺数绕流情况具备相对较高的航程和航时因子,并且保证了一定的纵向静稳定裕度;同时由于前翼流动分离形态较后翼提前,构型在失速条件下具备自恢复能力,满足设计指标要求。
非设计速度下的计算结果表明,设计巡飞弹干净构型在所研究的飞行速度范围内升阻比均较高,具备在较宽的飞行速域内工作的能力。

图7 不同速度下构型气动力变化曲线
4 结论
文中针对一种适于单兵携带的小型攻击型巡飞弹完成了气动外形设计,并利用CFD手段对其气动特性进行了评估与校核。计算分析结果表明所设计的巡飞弹构型具备良好的飞行性能。通过文中的分析和计算,可以得到以下结论:
1)对于大展弦比串列翼布局飞行器,前翼展弦比一般应大于后翼,使其在后翼之前失速,从而使在失速条件下能够维持纵向静稳定性并改出。
2)由于前翼尾流产生的下洗流动影响遍及整个后方流场,使得后翼实际攻角小于前翼,使其流动形态较前翼有所推迟;且随着前翼攻角的增加,此下洗效应逐渐显著,故前翼气动效率总高于后翼。
[1] 庞艳珂, 韩磊, 张民权, 等. 攻击型巡飞弹技术现状及发展趋势 [J]. 兵工学报, 2010, 31(增刊2): 149-152.
[2] 柏席峰. 美国大兵手中又一把小利刃——“弹簧刀”巡飞弹 [J]. 兵器知识, 2012(8): 51-54.
[3] 史文东, 卢笙, 王华. 巡飞器气动特性研究 [J]. 中国水运, 2008, 8(12): 137-139.
[4] 魏明, 王华. 巡飞器无舵偏情况下的气动数值分析 [J]. 飞行力学, 2010, 28(2): 59-62.
[5] 纪秀玲, 何光林. 管式发射巡飞弹的气动特点及设计 [J]. 北京理工大学学报, 2011, 28(11): 953-956.
[6] 李广佳, 李锋, 石文. 串置翼型数值模拟及气动特性分析 [J]. 飞机设计, 2006(1): 19-24.
[7] Daniel F Scharpf, Thomas J Muellert. Experimental study of a low reynolds number tandem airfoil configuration [J]. Journal of Aircraft, 1992, 29(2).
[8] Takanashi S. An iterative procedure for three-dimensional transonic wing design by the integral equation method, AIAA Paper-84-2155 [R]. 1984.
[9] Walters D K, Leylek J H. Impact of film-cooling jets on turbine aerodynamic losses [J]. ASME Journal Turbomach, 2000, 122: 53-55.
[10] Volino R J. A new model for free-stream turbulence effects on boundary layers [J]. ASME Journal Turbomach, 1998, 120: 613-620.
[11] Mcghee R J, Walker B S, Millarid B F. Experimental results for the Eppler387 airfoil at low Reynolds numbers in the Langley low-turbulence pressure tunnel, NASA-TM4062 [R]. 1988.
The Aerodynamic Design of Small Man-portable Loitering Munition
TAO Fuxing,ZHANG Heng,LI Jie
(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)
In this paper, aerodynamic design and analysis of a man-portable small loitering munition were performed. The basic design indicators and tandem wing aerodynamic layout of the loitering munition were given and the aerodynamic design was completed considering effect of low Reynolds number and packaging properties. The aerodynamic force of the designed configuration was simulated under design and off-design conditions. The result of calculation shows that the designed configuration can be considered to meet the design requirements and have good flight performance. The conclusions from the design can provide references for applications in engineering.
loitering munitions; low Reynolds number; tandem wing; numerical simulation
2015-05-27
陶福兴(1981-),男,安徽泗县人,工程师,硕士研究生,研究方向:弹箭兵器气动力。
V211.3
A

