旋转伞-末敏子弹系统动力学建模与仿真

马晓冬,郭 锐,刘荣忠,吕胜涛

(南京理工大学智能弹药技术国防重点实验室,南京 210094)



旋转伞-末敏子弹系统动力学建模与仿真

马晓冬,郭 锐,刘荣忠,吕胜涛

(南京理工大学智能弹药技术国防重点实验室,南京 210094)

为提高末敏子弹稳态扫描段的整体性能,设计一种由旋转伞和圆形减速伞构成的组合伞系统。基于ADAMS软件,对2种旋转伞-末敏子弹系统进行多体动力学建模,计算零初速自由下落过程,并通过伞塔试验验证模型的正确性。模拟2种系统的稳态扫描过程,得到弹道特性并进行对比分析。结果表明:双伞-子弹系统具有更好的整体运动性能,稳态落速低,滞空时间长,在地面形成更密集的扫描轨迹。

伞-弹系统;拉格拉日方法;多体动力学;伞塔试验

0 引言

末敏子弹从母弹抛出经减速减旋后,减速导旋主伞张开。伞-弹系统受到空气动力及系统阻尼的影响,运动一段时间后匀速下落,并绕着伞轴稳定旋转,子弹在地面形成规则的扫描轨迹,即达到稳定扫描状态,探测地面装甲目标[1]。为了末敏子弹能够有效的打击地面装甲目标,了解并且提高其稳态扫描段的运动性能至关重要。

伞-弹系统是一种复杂的动力学系统,国内外学者从理论建模方面对其进行了一系列研究。Karl Friedrich Doherr等[2]建立了旋转伞-子弹系统9自由度模型,计算得到弹道特性和动力学行为。V.Dobrokhodov等[3-4]针对可控圆形伞-物系统进行6自由度动力学建模,并开发出相应的控制硬件。舒敬荣等[5]建立末敏弹系统的伞、伞盘、弹三体运动学模型。唐乾刚等[6]建立伞-弹系统9自由度动力学模型,并将其用于末敏弹目标识别分析中。D.W.Pillasch等[7]基于Lagrange方法建立旋转伞-子弹系统5刚体10自由度动力学模型,给出建模思路和计算结果。

为了解旋转伞的减速导旋性能,提高末敏子弹稳态扫描段的整体运动性能,文中在原有旋转伞系统的基础上,设计了一种由圆形伞和旋转伞组成的双主伞系统,建立旋转伞-末敏子弹系统的5刚体15自由度模型和双伞-末敏子弹系统的6刚体21自由度模型,利用动力学分析软件对动力学模型进行求解,得到稳态扫描段的弹道结果。

1 降落伞-末敏子弹系统

旋转伞-末敏子弹系统由旋转伞、伞盘、摩擦盘、连杆和末敏子弹组成,见图1所示的系统1。减速减旋结束向稳态扫描状态过渡过程中,系统各部分的相对运动情况的描述见文献[8]。

图1(b)的系统2为双伞-末敏子弹系统。圆形伞位于旋转伞的上方,通过伞绳与后者的中心绳连接。

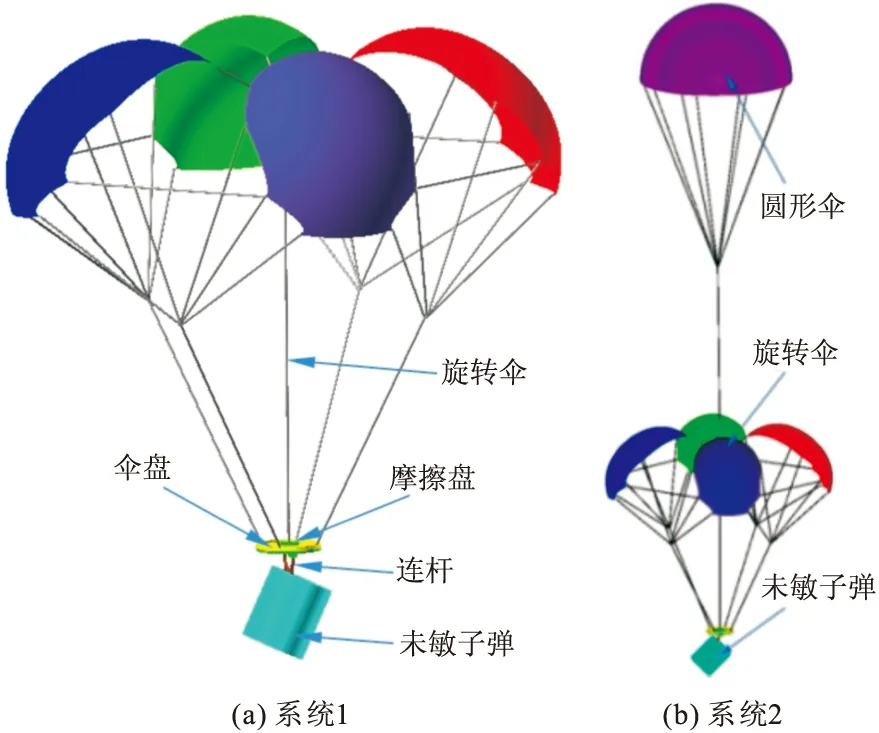
图1 旋转伞-末敏子弹系统示意图

2 仿真模型

2.1 模型假设

充分考虑伞-弹系统各部分之间的连接,建立系统1的5刚体动力学模型1和系统2的6刚体动力学模型2。引入以下假设:

1)重力加速度为常数,忽略地球的科氏加速度和曲率; 2)不考虑伞的透气性,将其视为刚体,将伞绳视为阻尼弹簧; 3)不考虑伞盘、摩擦盘和连杆的空气动力,伞和末敏子弹的气动参数为常数; 4)忽略弹体、摩擦盘等尾流对伞的影响。

2.2 虚拟样机建立

ADAMS基于拉格拉日力学思想建模,将伞-弹系统实体模型导入,根据实际的质量特性设置相应参数、添加运动幅并施加空气动力,建立虚拟样机,进行动力学仿真。

根据假设条件2),用半球面代替旋转伞伞衣幅;伞衣幅通过4根阻尼弹簧与伞盘连接;伞盘与摩擦盘间、摩擦盘与连杆间及连杆与弹体间均为转动运动副Revolute连接;考虑伞盘与摩擦盘间运动副的摩擦力;圆形伞通过1根阻尼弹簧与旋转伞连接;在弹体与摩擦盘之间添加接触设置SolidContact,否则在仿真初期二者之间会发生穿透,影响计算结果。

3 伞塔试验

为验证动力学模型模拟伞-弹系统真实运动的有效性,设计一种伞塔投放试验,如图3所示,采用100 m高的伞塔进行投放试验。将旋转伞-末敏子弹系统从塔顶投下,正在下落的双伞-末敏子弹系统如图4所示,通过姿态参数存储测量仪得到系统转速变化和扫描角变化[9],高速摄像仪和标尺测量系统的下落速度。

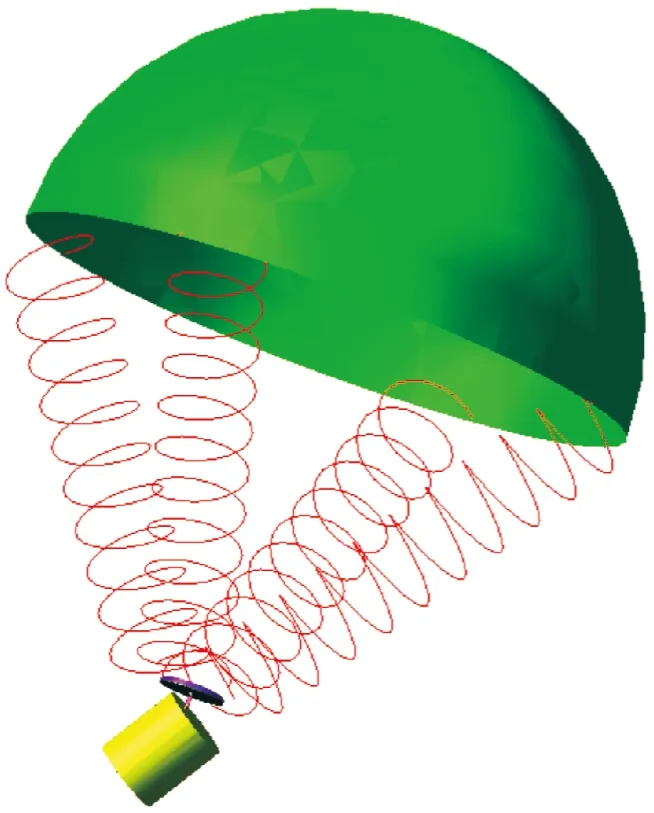
图2 系统1的虚拟样机示意图

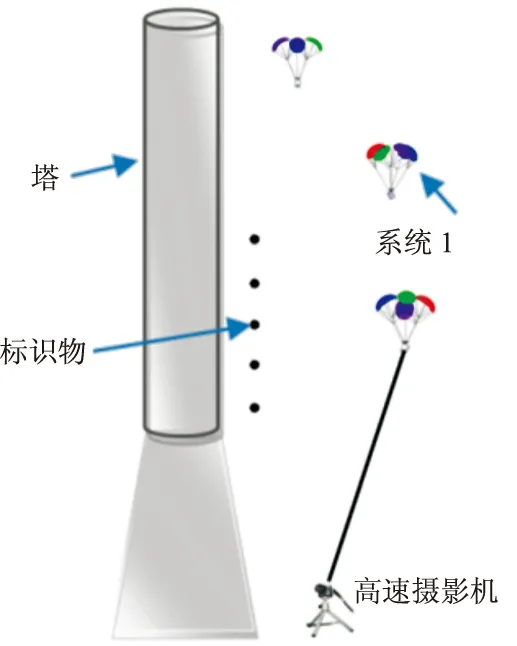
图3 伞塔试验布置

图4 正在下落的系统2

4 结果与分析

4.1 零初速自由下落

旋转伞-末敏子弹系统从伞塔抛下,初始速度近似为零,故设定仿真初始条件:Vi=0。计算时间为10 s,时间步长为0.001 s。

计算结束可直接输出末敏子弹的转速、扫描角和落速等弹道结果。图5～图8为模型计算与试验的结果对比。试验模型在伞塔抛下初期,降落伞没有完全充气展开,此时其气动力系数与完全展开时相差很大,结合假设条件3)知,试验初段测得数据与理论计算结果误差较大,所以重点分析稳定阶段的结果。

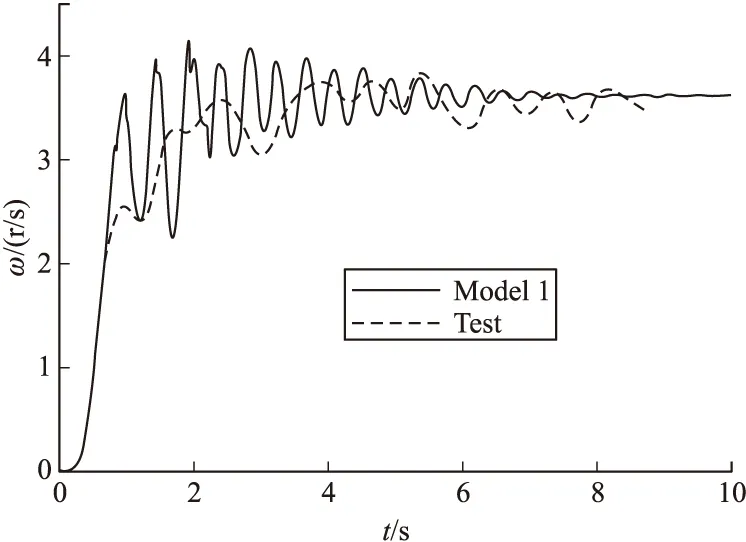
图5 系统1子弹的转速

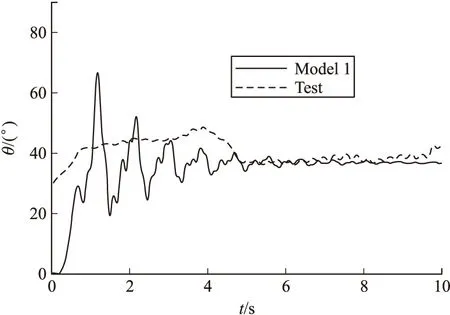
图6 系统1子弹的扫描角

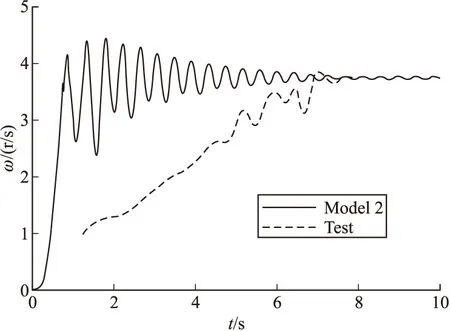
图7 系统2子弹的转速

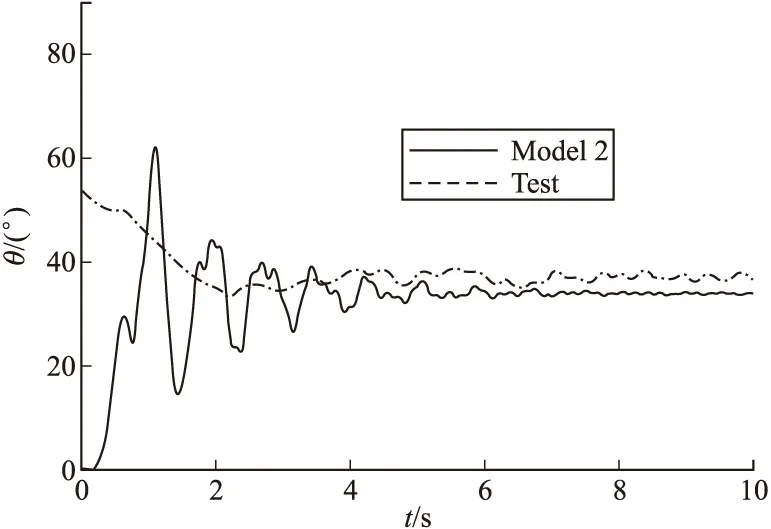
图8 系统2子弹的扫描角

由图5看出:模型1仿真计算中,子弹转速从6 s开始趋于稳态值3.6 r/s,试验稳态转速在3.6 r/s上下小幅变化。由图6看出:扫描角从6 s开始趋于稳态值37.0°,试验稳态扫描角约38.5°,误差3.9%。此外,仿真稳态落速为12.29 m/s,试验稳态落速为11.02 m/s,误差为10.3%。

由图7得出:模型2仿真计算中,末敏子弹的转速约从7 s开始趋于稳态值3.2 r/s;试验中约从3 s开始子弹转速一直增大到稳态,说明3 s时系统2的降落伞系统充气基本完成。由于具有2个降落伞,受到的空气阻力大,所以下落加速度相对模型1小。转速随着下落速度增大而增大,稳定值约3.2 r/s。由图8得到:模型2子弹稳态扫描角为34.1°,试验稳态值为37.3°,误差为8.6%。此外,系统2稳态落速为11.17 m/s,试验稳态落速为10.80 m/s,误差为3.3%。

误差的主要因素是动力学模型的简化、试验模型的加工误差、天气(如风)等。

综上,数值计算得到的末敏子弹稳态转速、落速及扫描角与试验数据吻合较好,所以模型1和模型2能较真实地反映2种伞-弹系统在稳态扫描段的运动特性。

对比图5和图7:伞塔试验中,系统1达到稳定的时间明显短于系统2,这主要是因为单伞系统下落速度快,伞系统很快完成充气,从而进入减速导旋、稳态扫描过程;子弹转速曲线波动,这是由于伞-弹系统在下落过程中伴随着绕铅垂轴的圆锥运动,同时子弹绕着柱铰亦做小范围的转动,随着系统下落,曲线波动越来越小,趋于稳定。

对比图6和图8:系统1子弹扫描角略大于系统2,这是由于系统1子弹的转速和落速均较高,其绕铅垂轴的圆锥运动的幅度亦较大,使得稳态运动时扫描角较大。

4.2 实际工况

实际工作中,末敏子弹在减速减旋后,其减速导旋主伞张开时,系统具有一定的初始速度和转速。为模拟末敏子弹实际工作状态,设置伞-弹系统的初始条件:Vx=36.76 m/s,Vy=120.25 m/s,Vz=-41.63 m/s,ωz=14.24 r/s,系统初始位置(0 m,0 m,300 m)。计算得到如图9～图15所示的弹道结果。

当t=10 s时,系统1和系统2均进入稳定状态,在地面的扫描轨迹逐渐规则,主要弹道参数如表1所示,均满足末敏子弹稳态扫描的要求。

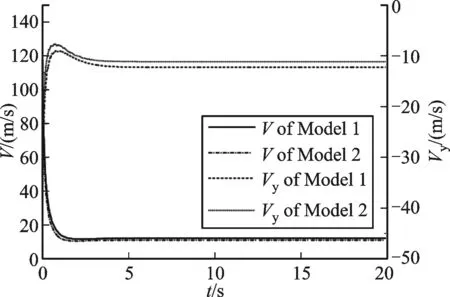
图9 子弹速度

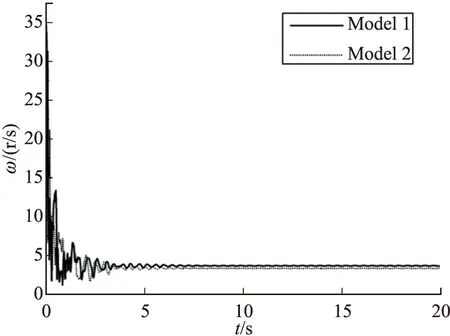
图10 子弹转速

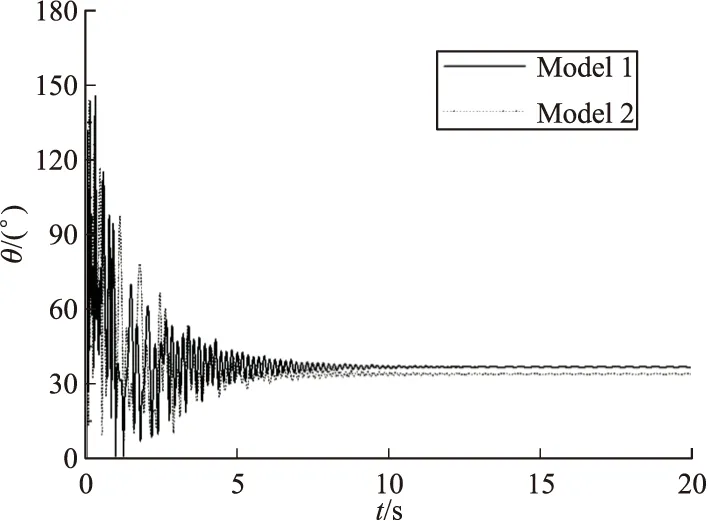
图11 子弹扫描角

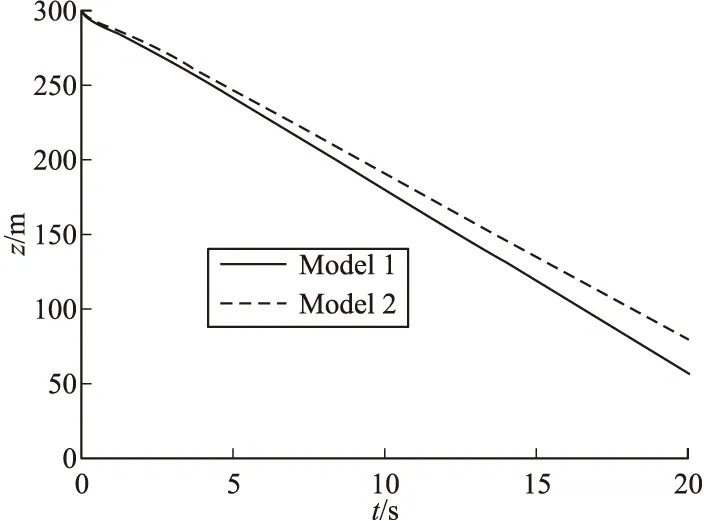
图12 子弹高度

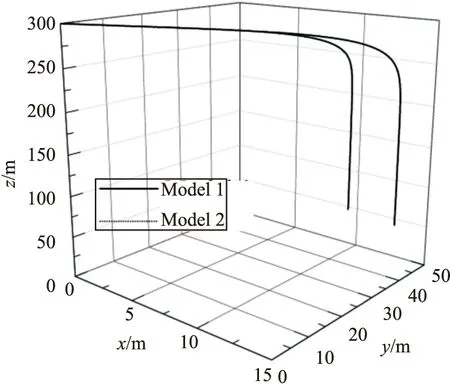
图13 伞弹系统空中轨迹(0～20 s)

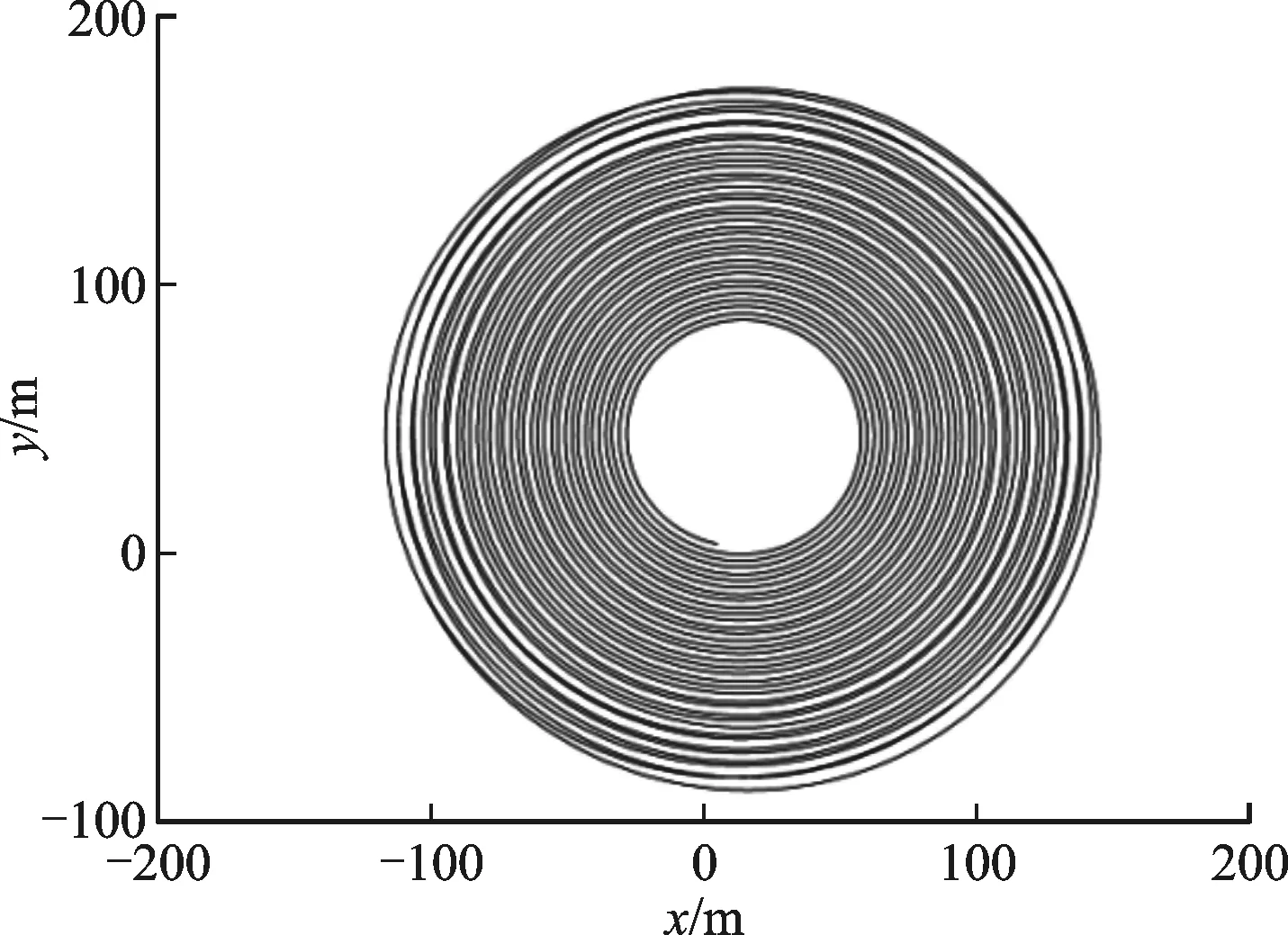
图14 模型1的地面扫描轨迹(10～20 s)

由图9得出:由于旋转伞的减速作用,系统的速度急剧下降,约在t=4 s时,速度下降到稳定值,由于有2个降落伞,系统2的减速效果略好于系统1。

由图10和图11得出:旋转伞和末敏子弹受到空气动力矩的阻尼作用,同时摩擦盘受到伞盘摩擦阻力的作用,末敏子弹的转速急剧减小;此时系统的速度和空气动力较大,末敏子弹的姿态很不规律,发生大范围的翻滚,子弹扫描角大于90°;约t=4 s时,末敏子弹的转速减小至稳定值附近,扫描角亦逐渐趋于稳定,二者在稳定值附近震荡且幅度逐渐减小,最终系统达到稳定状态。

结合图5～图11,系统在2种边界条件下的稳态落速、转速和扫描角均相等,说明文中设计的旋转伞-末敏子弹系统具有运动稳定性,且对于相同结构的旋转伞-末敏子弹系统,在相同介质和不同初始运动条件下,稳定状态相同。

由图12和图13得到:由于减速效果好,系统2的滞空时间长于系统1,水平方向位移小于系统1,末敏子弹稳态扫描时间长,更有利于搜索目标。

对比图14和图15:系统1和2具有相同的转速落速比,但系统2子弹的稳态扫描角略小于系统1,所以系统2子弹的稳态地面扫描轨迹比系统1的密集,更不易漏扫目标,即系统2的稳态扫描效果好于系统1。

5 结论

1)5刚体15自由度动力学模型和6刚体21自由度动力学模型均符合旋转伞-末敏子弹系统的实际结构,能更加真实地反映末敏子弹稳态扫描段的弹道特性,为末敏子弹总体设计与扫描装置的设计提供帮助。

2)双伞系统的减速效果优于单伞系统,使得末敏子弹系统稳态落速低,滞空时间长,为子弹的稳态扫描提供更长的时间。

3)旋转伞的转速落速比约为定值,在低转速低落速情况下的圆锥运动幅度小,使子弹在地面形成更密集的扫描轨迹。

4)作为末敏子弹的减速导旋系统,由圆形伞和旋

转伞组成的双伞系统的整体性能优于单一的旋转伞,故可以考虑将双伞系统作为末敏子弹系统的减速导旋伞。

[1] 王儒策, 刘荣忠. 灵巧弹药的构造及应用 [M]. 北京: 兵器工业出版社, 2001.

[2] KARL FRIEDRICH D, HARTMUT S. Nine-degree-of-freedom simulation of rotating parachute system [J]. Journal of Aircraft, 1992, 29(5): 774-781.

[3] Dobrokhodov V, Yakimenko O, Junge C. Six-degree-of-freedom model of a controlled circular parachute, AIAA 2002-4613 [R]. 2002.

[4] Dobrokhodov V, Yakimenko O, Junge C. Simulink implementation of the 6DOF model of controlled circular parachute, AIAA 2002-4970 [R]. 2002.

[5] 舒敬荣, 王宝贵, 韩子鹏, 等. 伞-弹系统三体运动分析 [J]. 航空学报, 2001, 22(6): 481-485.

[6] 唐乾刚, 张青斌, 张晓今, 等. 伞-弹系统九自由度动力学模型 [J]. 兵工学报, 2007, 28(4): 449-452.

[7] PILLASCH D W, SHEN Y C. Parachute/submunition system coupled dynamics, AIAA 1984-0784 [R]. 1984.

[8] 殷克功. 末敏子弹运动特性分析 [D]. 南京：南京理工大学, 2008.

[9] 郭锐, 刘荣忠, 胡志鹏, 等. 涡环旋转伞开伞稳定性及减速导旋运动特性研究 [J]. 空气动力学学报, 2013, 31(6): 733-738.

Dynamics Modeling and Simulation for Rotating Parachute-terminal-sensitive Submunition Systems

MA Xiaodong,GUO Rui,LIU Rongzhong,LYU Shengtao

(Ministerial Key Laboratory of ZNDY, Nanjing University of Science and Technology, Nanjing 210094, China)

To increase the whole performance of terminal-sensitive submunition during steady scanning stage, a compound parachute system composed of a circle drag parachute and a rotating parachute was designed. Based on ADAMS software, the dynamic models of two multi-body systems were set up, and the falling process with 0 initial velocities was simulated. Parachute tower test was designed to verify the dynamic models. Then the two models were used to simulate the steady scanning process, and the ballistic characteristics were obtained, and their kinetic performances were analyzed contrastively. The results show that the double parachute system has better kinetic performance comparatively, for its stable falling velocity is low and could stay in the air for a longer time, and the ground scanning trace is denser

parachute-submunition system; Lagrange method; multi-body dynamics; parachute tower test

2015-03-10

国家自然科学基金(11102088);江苏省研究生培养创新计划项目(CXLX12-0210)资助

马晓冬(1988-),男,黑龙江宝清人,博士研究生,研究方向:弹药灵巧化与智能化。

V212

A