活性粉末混凝土抗折疲劳寿命的对数正态分布研究
杨科文,罗许国
(湖南科技大学 土木工程学院,湘潭 411201)
参 考 文 献
活性粉末混凝土抗折疲劳寿命的对数正态分布研究
杨科文,罗许国
(湖南科技大学 土木工程学院,湘潭 411201)
活性粉末混凝土(简称RPC)是一种新型水泥复合基材料,由于具有超高强度、高韧性、高耐久性等优良性能而越来越多受到学者的关注与研究,现在开始也越来越多的被应用于实际工程中.通过三种不同钢纤维体积掺量的试件进行抗折疲劳试验研究了RPC的疲劳寿命分布.疲劳试验获得了试件的抗折疲劳加载次数,并用疲劳统计学理论验证了RPC疲劳寿命的对数正态分布.
活性粉末混凝土;钢纤维;抗折疲劳试验;疲劳寿命;对数正态分布
RPC是19世纪20年代法国BOUYGUES公司研发出的一种新型混凝土.它具有超高的强度、较低的脆性、良好的韧性以及优异的耐久性能,具有广阔的研究开发与应用前景.RPC是由水泥、粉煤灰、石英砂、硅粉、高效减水剂等组成,并通过掺入钢纤维以提高RPC的延性和韧性[1-2].
在土木工程中很多的混凝土结构承受循环荷载的作用,如机场路面、公路和铁路桥梁等承受反复车辆荷载作用,这些反复荷载会导致混凝土结构性能不断退化,使结构在低于静载强度的情况下发生脆性破坏.因此对RPC的疲劳寿命进行研究是很有必要的.疲劳寿命影响因素众多,即使在试验条件完全相同的情况下,试件的疲劳寿命也存在着很大的离散性,想要在实际应用中用结构材料的物理量来定量的分析疲劳寿命具有一定的难度.为了正确反映在不同纤维掺量下疲劳寿命的变化规律,运用概率理论对混凝土疲劳寿命与可靠性进行宏观分析和估计就显示出逻辑上、理论上和实质上的必要性和合理性.
1 疲劳寿命的对数正态分布概率模型
1.1 正态分布
正态分布的概率密度函数为[3]:
(1)
上式中,x为寿命值,μ、σ为正态分布的参数.随机变量X服从参数为(μ,σ2)的正态分布.
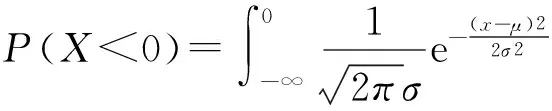
1.2 对数正态分布
综上所述,就理论而言,用正态分布来描述这些随机变量是不严格的.然而对数函数可以将实数域中的大于零的区间(0,+∞)映射为整个实数域(-∞,+∞).如对恒大于零的随机变量即疲劳寿命X作变换:Y= lnX,则Y的取值范围为:(-∞,+∞).符合正态分布的要求.如Y(即lnX)服从正态分布,其概率密度函数为:
(2)
对数正态分布有一个明显的缺点,即当F(Ni)= 0时,在理论上Ni=-∞,或当Ni= 0时,F(Ni) > 0,即少量试件未经疲劳试验就已经破坏了.不过,对数正态分布仍是目前较为常用的分布形式.这是由于基于正态分布的统计推断方法比较成熟,且按对数正态分布处理疲劳寿命数据时,得到的结果一般较为保守.
2 试验概况
2.1 材料准备与配合比设计
RPC的配合比见表1,制备RPC的主要材料为:强度等级为42.5级的普通硅酸盐水泥;平均粒径为0.1 μm的硅灰,其SiO2的质量分数>90%;40~70目的精制石英砂,其平均粒径为0.23~0.45 mm;可溶性聚羧酸系高效减水剂,当含固量为35%,掺量为2%时,减水率为25%以上;钢纤维为采用镀铜光面平直钢纤维,其直径为(0.16±0.005)mm,长度为(12±1) mm,抗拉强度>2000 MPa.

表1 RPC材料配合比
2.2 试件设计与制作
(1)试件设计
试件尺寸为40 mm×40 mm×160 mm,钢纤维体积掺量设计为0%、1%、2% ,按此将设计组分为S0、S1、S2组,每组制作11个试件,每组3个用于静载试验8个用于抗折疲劳试验.
(2)试件制作与养护
各组试件均采用标准方法制作及养护.由于操作失误,本次试验RPC试件并没有进行热水养护,而是进行标准养护.

(3)试验方法
本试验仪器采用MTS810疲劳试验机,3点弯曲试验方式进行循环加载.跨距120 mm,高度40 mm,跨高比为3.荷载施加于跨中,所施加疲劳荷载波型为正弦波,加载频率为4 Hz.
3 试验结果及分析
3.1 抗折强度试验结果
通过抗折试验所得试验数据及计算结果如表2所示.
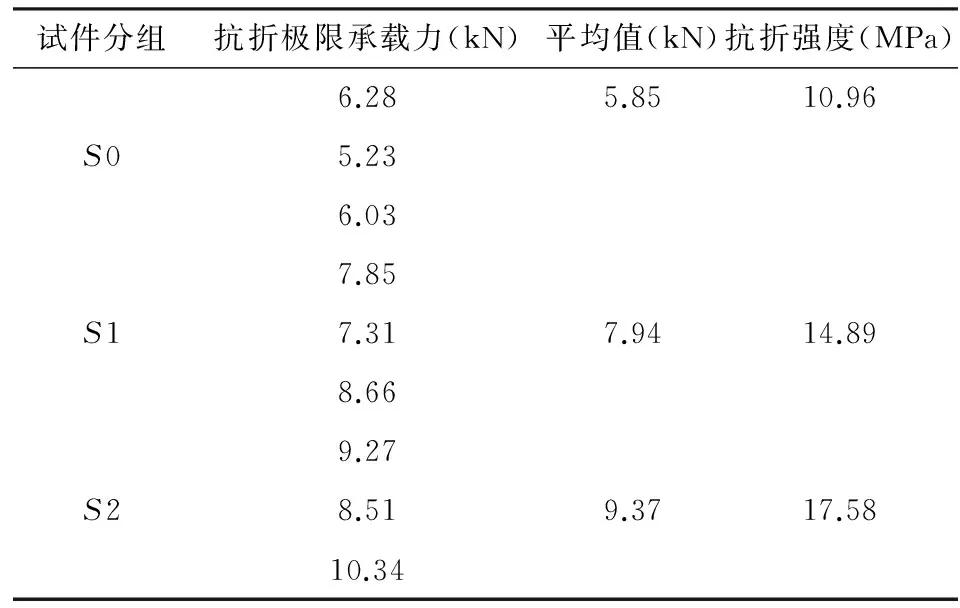
表2 抗折强度试验数据记录及计算
3.2 抗折疲劳试验现象及结果分析
将抗折疲劳试验的加载参数和试验获得的6个试件组的疲劳加载数据按从小到大整理如表3所示.

表3 抗折疲劳试验结果统计表
素RPC试件的抗折疲劳破坏也表现出了明显的偏脆性破坏,裂缝在跨中位置产生后会随着荷载循环次数的增加快速的扩展,并很快失去承载能力而破坏.但钢纤维体积掺量增加为2%时,其破坏形式表现出了较为明显的塑性破坏.观察疲劳试验现象发现,从疲劳循环荷载开始施加到RPC试件跨中底部出现竖向微裂纹这一过程中,试件的跨中挠度并没有出现明显的变化.随着荷载的继续,微裂缝会开始沿着梁高方向缓慢的扩展增长,并能够带裂缝继续承受荷载.这是由于裂缝处的钢纤维代替受拉区的混凝土承受拉力,直至部分钢纤维被拉断或拔出.此后裂缝会继续扩展直至贯通整个试件而至失去承载能力,这期间试件挠度会急速变大.此过程RPC表现出了良好的塑性性能.由此可知钢纤维的掺入在一定程度上改变了RPC试件的抗折疲劳破坏形式.
由疲劳寿命统计数据可知,钢纤维体积掺量的增加使RPC试件的疲劳寿命总体上保持了增加的势头.钢纤维的弹性模量和抗拉强度比混凝土基材大了约5倍,因此它有很好的阻裂效果,在疲劳裂纹的扩展过程中起到了延缓宏观裂缝失稳扩展的作用.试验表明,钢纤维的掺入有效地增强了RPC的韧性,提高了RPC的疲劳寿命.
通过观察疲劳试件从加载开始到裂缝发展失去承载能力过程以及对试验数据的分析,我们可以从宏观上将RPC试件的疲劳损伤演化过程分为三个不同阶段,分别是裂纹潜伏阶段、裂纹稳定扩展阶段和失稳破坏阶段.第一阶段为裂纹潜伏阶段.它是RPC试件内部的微观裂缝发展并贯通,慢慢演变出现宏观裂缝的过程.该阶段较为短暂,约占总疲劳寿命的15%左右.第二阶段为裂纹稳定扩展阶段.在一个循环过程中,疲劳荷载从Pmax变到Pmin时裂缝由张开转为闭合,随着循环荷载的继续裂缝也不断的开合.裂纹此时也开始扩张增长.该阶段的荷载循环次数是占据了总疲劳寿命的绝大部分,约为75%左右.第三阶段为失稳破坏阶段.此时的主裂缝迅速扩展使试件失去了承载能力,试件挠度也快速的增长,发生了疲劳破坏,约为疲劳总寿命的10%左右.试件疲劳破坏后可以发现,裂纹处的温度要比其他部分温度高些,这说明抗折疲劳过程中裂纹处有热量释放出来[4].
3.3 各组试件抗折疲劳寿命符合对数正态分布的检验
对数正态分布的积累分布函数为:

(3)

由于φ(z)为严格单调增函数,故其反函数存在.对公式(3)等号两边取反函数,并令:Y=φ-1[F(lnNp)],X=lnNp,A=1/σlnN,B=μlnN/σlnN,则:Y=AX-B.其为一条关于X、Y的直线方程,亦即抗折疲劳寿命若遵循对数正态分布,Y与X必定形成一条直线.
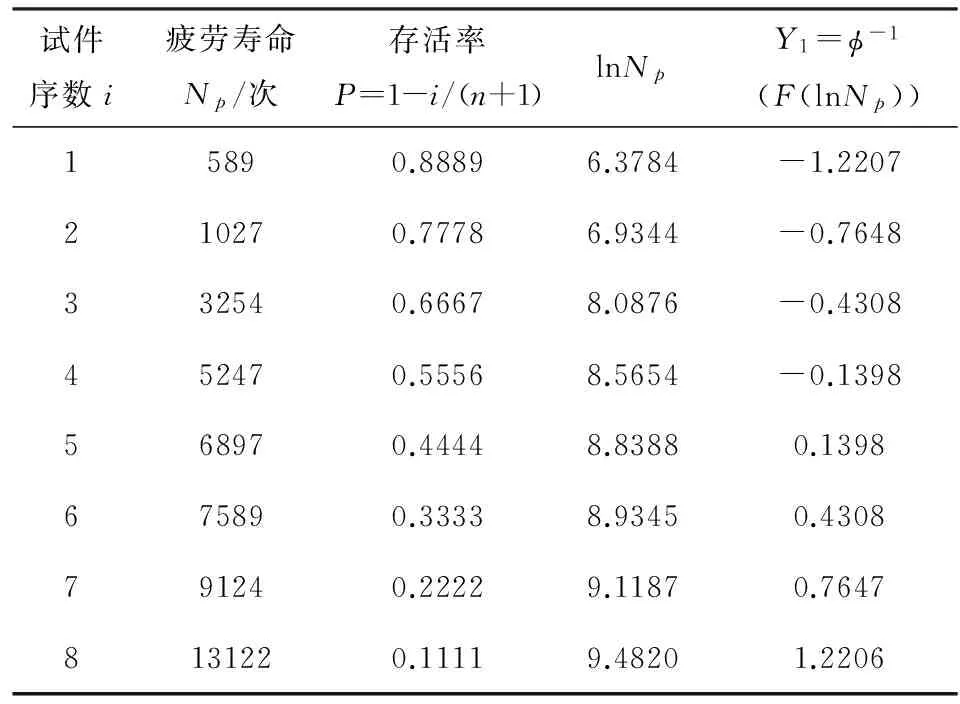
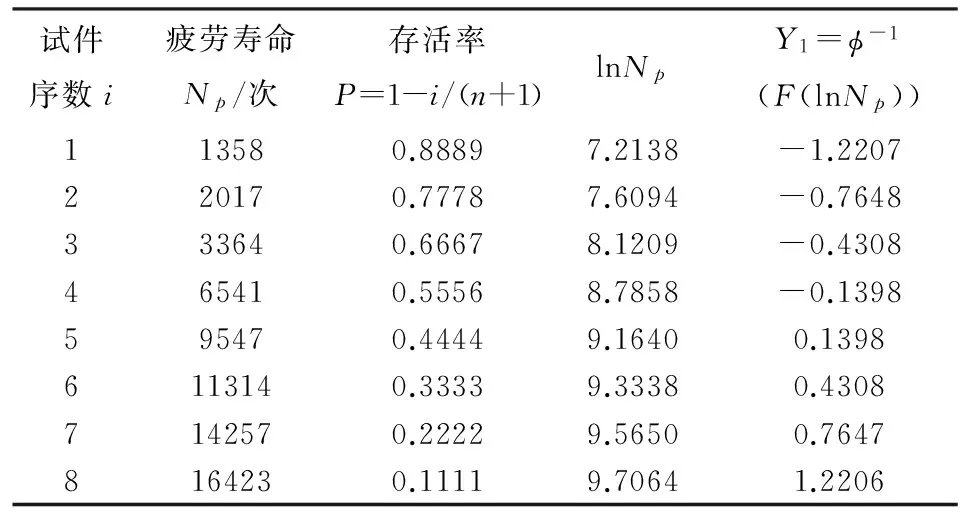
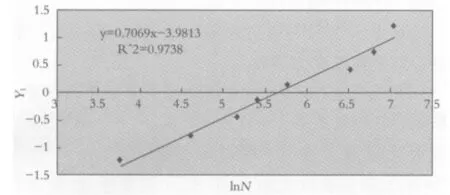
失效概率估计使用平均值,即样本点Xi(Xi (4) 则疲劳寿命Np所对应的存活率P可表示为: (5) 其中,n为某一应力水平下疲劳试验总数,i为疲劳试验数据试件序数. 综上所述,若抗折疲劳寿命服从对数正态分布,那么存在线性关系Y=AX-B.其中,X=lnNp,Np表示抗折疲劳寿命,通过试验获取.Y=φ-1(F(lnNp))可以通过计算得到.A、B需要通过(X,Y)的线性回归分析得出.根据以上推论用Excel计算各参数列表如表4、表5、表6所示,并图示见图1、图2、图3. 表4 S0试件组抗折疲劳寿命Np的对数正态分布检验 表5 S1试件组抗折疲劳寿命Np的对数正态分布检验 表6 S2试件组抗折疲劳寿命Np的对数正态分布和威布尔分布检验 图1S0试件组抗折疲劳寿命Np的对数正态分布检验 图2S1试件组抗折疲劳寿命Np的对数正态分布检验 图3S2试件组抗折疲劳寿命Np的对数正态分布检验 由图1~图3可知,回归分析结果中的相关系数r分别为0.9738、0.8936和0.9373,均在0.85以上,这表明lnNp与Y1=φ-1(F(lnNp))之间的线性相关关系显著.RPC试件的抗折疲劳寿命很好地服从了对数正态分布. (1)钢纤维的掺入有效地增强了RPC的韧性,提高了RPC的疲劳寿命.随着钢纤维的体积掺量的增大,抗折强度增大,抗折疲劳寿命也保持了增长的势头. (2)从宏观上可以将RPC试件的疲劳损伤演化过程分为三个不同阶段,分别是裂纹潜伏阶段、裂纹稳定扩展阶段和失稳破坏阶段,他们所占疲劳寿命的百分比分别为15%、75%和10%. (3)RPC试件的抗折疲劳寿命很好地服从了对数正态分布. 参 考 文 献 [1] 杜 婷,郭太平,林怀立,刘中心,周志强.混凝土材料的研究现状和发展应用[J].混凝土: 2006(5):7-9. [2] 施 涛,叶 青.活性粉末混凝土的研究和应用中存在的问题[J].建筑石膏与胶凝材料, 2003(5):23-25. [3] 张 伟.混凝土疲劳特性研究[D].河北:河北工业大学硕士论文,2006. [4] 石成恩.活性粉末混凝土(RPC)的弯曲疲劳寿命研究[D].福建:福州大学硕士论文,2004. Study on Logarithmic Normal Contribution of RPC with Flexural Fatigue Life YANG Ke-wen,LUO Xu-guo (School of Civil Engineering,Hunan University of Science and Technology, Xiangtan 411201, China) Reactive Powder Concrete (RPC) is a new type of composite cement-based material.Because of its ultra-high strength, high toughness, high durability and other excellent properties,RPC attracts more and more attention and is studied by many scholars.And now it has been used in more and more practical engineering fields. The paper studies the fatigue life distribution of RPC by testing the three different content of steel fiber volume specimens. Through the fatigue test the flexural fatigue loading times of the specimens is obtained, and the logarithmic normal distribution of fatigue life of RPC is varified by fatigue statistical theory. RPC;steel fibre;flexural fatigue test;fatigue life;logarithmic normal contribution 2015-04-21 湖南科技大学研究生创新基金资助项目(S130011). 杨科文(1990-),男,硕士研究生,研究方向:桥梁与隧道工程. TB321 A 1671-119X(2015)03-0091-04


4 结 论

