永磁同步电机无电流传感器控制系统运行性能分析*

徐 迅 ，阮建国 ，鲁文其， ，虞志源

(1．卧龙电气集团有限公司，浙江杭州310052;2．浙江省机电设计研究院有限公司，浙江杭州310009;3．浙江理工大学机械与自动控制学院，浙江杭州310016)

0 引 言

纺织行业是一个价格敏感型行业，尽可能地降低成本是所有企业所追求的目标。为此，该场合运用的伺服系统需要低成本的控制技术。而对伺服系统而言，一般需要一个物理传感器和相应的调理电路来采集并反馈电机的控制信号形成一个闭环控制系统，常用的传感器有位置传感器和电流传感器，如果能去掉这些传感器就可以减少成本，这就需要引入无传感器控制技术，而无传感器技术就相应地包括无位置传感器技术［1-8］和无电流传感器技术。如其中有文献提出了一种基于新型滑模观测器算法的无位置传感器PMSM 矢量控制调速系统并实验验证了该系统的有效性。但在某些场合，如经编机伺服系统、缝纫机伺服系统等，由于成本和定位控制精度的要求，应考虑保留位置传感器而去掉电流传感器，即无电流传感器控制。如文献［9-10］以全自动高速平缝机为对象，提出了一种新颖的无电流传感器估算方法并构成伺服系统进行了测试，分析和实验结果表明，该系统简单可行且有较好的控制性能。

为了使系统更紧凑经济［11-15］，本研究提出一种基于相电流算法重构的无电流传感器的永磁同步电机速度伺服系统方案，建立各组成部分的仿真模型，进行系统的性能分析。

1 相电流重构理论

永磁同步电机(PMSM)在d－q 坐标系下的状态方程如式(1，2)所示，对其进行改进得到的相电流重构算法的状态方程如式(3，4)所示，相电流重构算法的输入变量是电机相电压ud、uq和电角速度ωre，输出变量是电流id和iq，其原理框图如图1 所示。

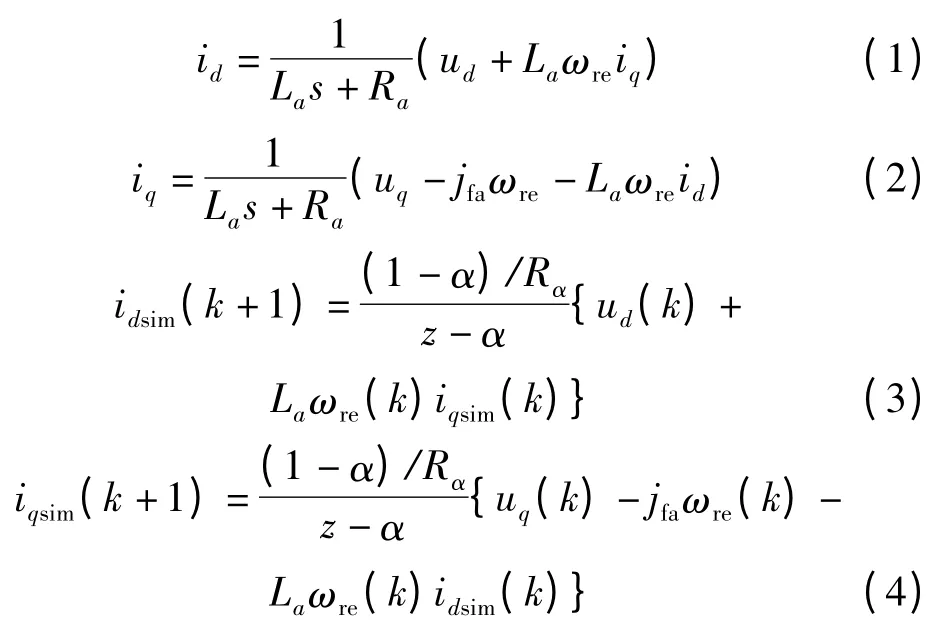
式中:ud，uq—电机相电压;ωre—电机角速度;La，Ra—电机相电感和电阻;jfa—电机磁链;idsim，iqsim—估算交直轴电流;α—估算调整因子。

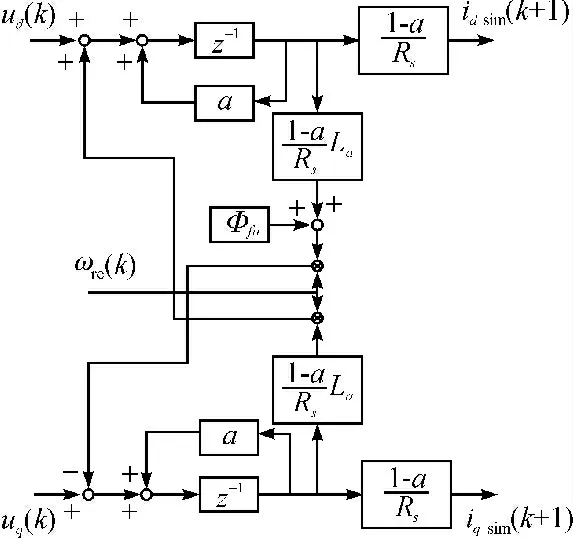
图1 相电流重构算法原理框图

2 空间矢量调制算法

为了使三相永磁同步电机能够很好的工作，需要电机转子产生圆形旋转磁场，而三相桥式逆变电路在一个工作周期内可以产生6 个基本的电压空间矢量和2 个零矢量，进而形成正六边形磁链。显然如果使用这8 个基本电压矢量去控制电机的旋转，电机的脉动很大，且电压利用率和开关管利用率都很低。为此人们提出电压空间矢量脉宽调制技术(space vector pulse width modulation，SVPWM)，SVPWM 引入“一个开关时间周期内的平均电压空间矢量”的概念，并设法使平均电压空间矢量等于期望的电压空间矢量，通过选取同一扇区相邻的两个非零矢量和相应的零矢量来合成一个等效的空间旋转电压矢量，这样就能形成更加逼近圆形的旋转磁场。该算法主要有以下实现流程:

2．1 判断当前电压所在扇区的判断

三相电压通过式(5)变换矩阵变换为Uα，Uβ:

再通过式(6)求得Vref1，Vref2，Vref3:

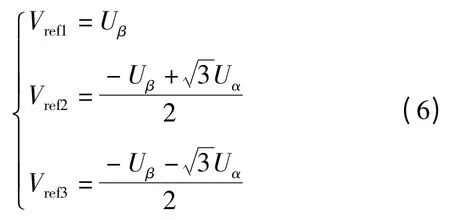
当Vref1＞0，A=1，否则A=0;

当Vref2＞0，B=1，否则B=0;

当Vref3＞0，C=1，否则C=0;

那么电压对应的扇区号N=4C+2B+A。

2．2 计算开关电压矢量作用时间的计算

首先定义变量X，Y，Z 如下:

则各扇区相邻电压矢量作用时间为t1，t2，空间矢量作用时间如表1 所示。

表1 空间矢量作用时间

2．3 计算空间矢量比较器的切换点定义

定义变量Ta、Tb、Tc如下:

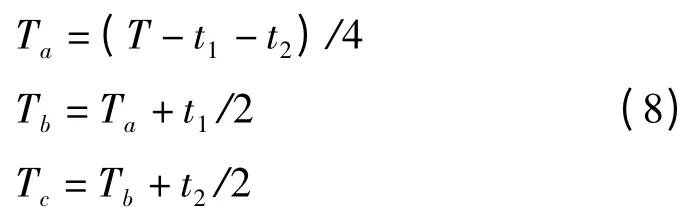
比较值作用时间如表2 所示。

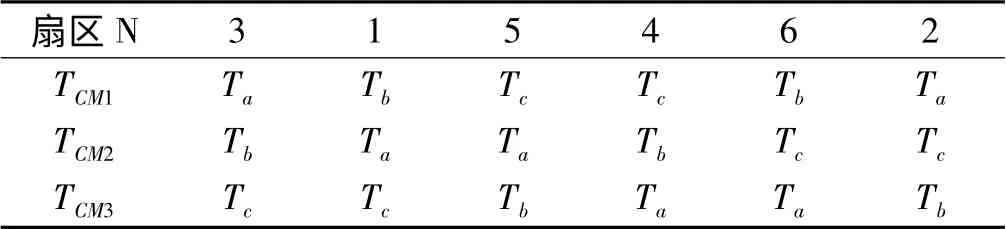
表2 比较值作用时间

则矢量切换点TCM1，TCM2，TCM3根据表2 赋值，从而得到三相桥臂的开关驱动信号。

3 无电流传感器闭环控制系统

本研究将相电流重构算法引入到伺服系统中，可得基于相电流算法重构的PMSM 伺服系统框图，如图2 所示。该系统采用id=0 的速度外环、电流内环两环控制结构的矢量控制方案，速度环和电流环采用PI 调节器进行设计，电流采用空间矢量算法进行调制，采用物理传感器对电机的转子位置信息进行检测与反馈。

图2 基于相电流重构理论的PMSM 伺服系统原理框图

4 系统建模

本研究在Simulink 环境下建立图2 所示伺服系统的仿真模型如图3 所示。包括永磁同步电机模型、虚拟码盘模型、空间矢量调制算法、速度控制器、电流控制器、相电流重构算法和纺织机械工况模拟等等。其中相电流重构算法的仿真模型如图4 所示。

图3 系统仿真模型

5 系统运行性能分析

为了全面地了解基于无电流传感器的永磁同步电机伺服系统的性能，本研究采用建模与仿真的方法对系统进行了稳态性能和动态性能方面的分析，具体如下:

5．1 稳态性能

给定转速在1 500 r/min 时，系统仿真运行得的实际速度和相电流重构估算波形如图5(a)，5(b)所示。从波形可知相电流重构算法估算的交直轴电流与实际电流相差较小，且实际速度波形比较平滑，稳态性能较好。

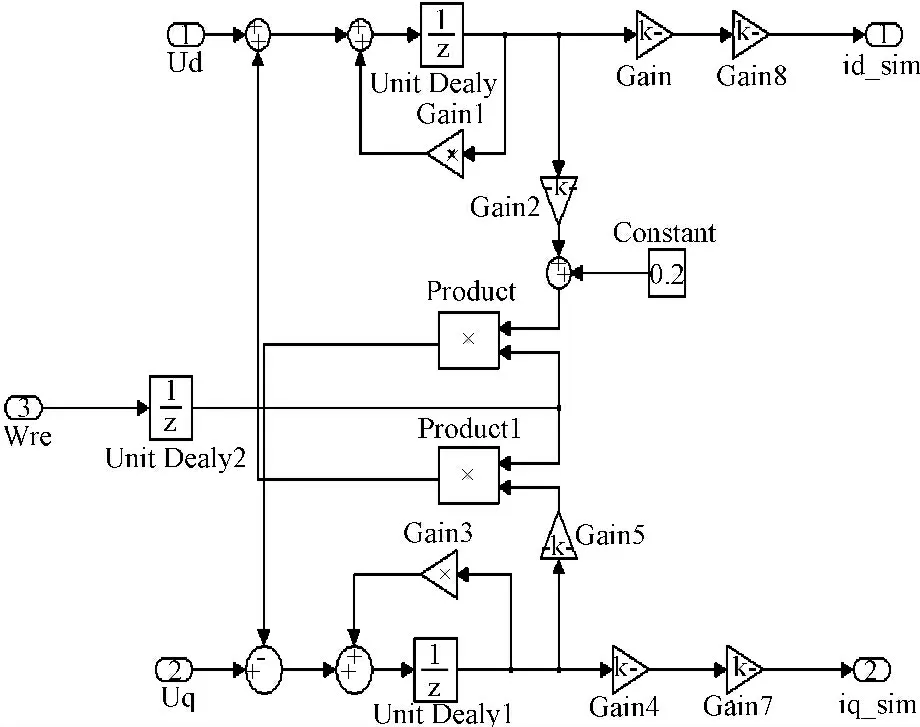
图4 相电流重构算法仿真模型

图5 无电流传感器伺服系统在给定转速1 500 r/min 运行时的仿真波形

系统给定转速在200 r/min 时，系统仿真所得到的实际速度和相电流重构估算波形如图6(a)、6(b)所示，从波形可知，相电流重构算法估算的交直轴电流与实际电流相差较大，但实际速度波形还是比较平滑，稳态性能还好。

系统给定转速在30 r/min 时，系统仿真所得到的实际速度和相电流重构估算波形如图7(a)、7(b)所示，从波形可知，相电流重构算法估算的交直轴电流脉动较大，与实际电流相差很大，且实际速度波形波动也较大，但总体还是稳定的。

5．2 动态性能

系统给定转速在500 r/min 与1 000 r/min 之间跳跃时，系统仿真所得到的相关波形如图8(a)、8(b)所示。由图8 可知，其速度动态性能较好，稳态时波形平滑。其电流估算值与实际值存在一定误差，但估算电流的响应速度较好，能够跟上实际电流的变化，系统总体性能较好。

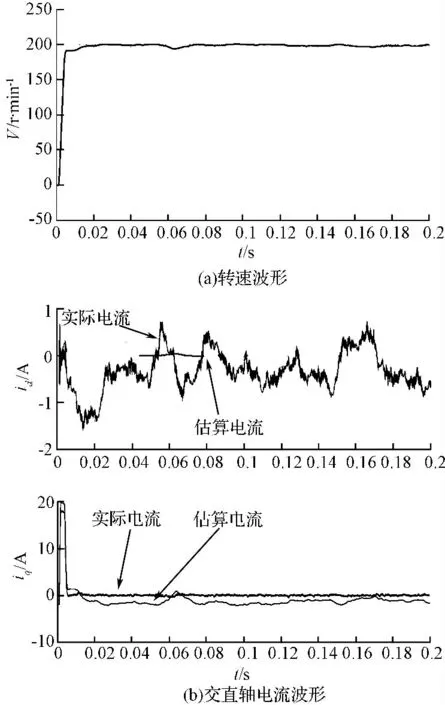
图6 无电流传感器伺服系统在给定转速200 r/min 运行时的仿真波形

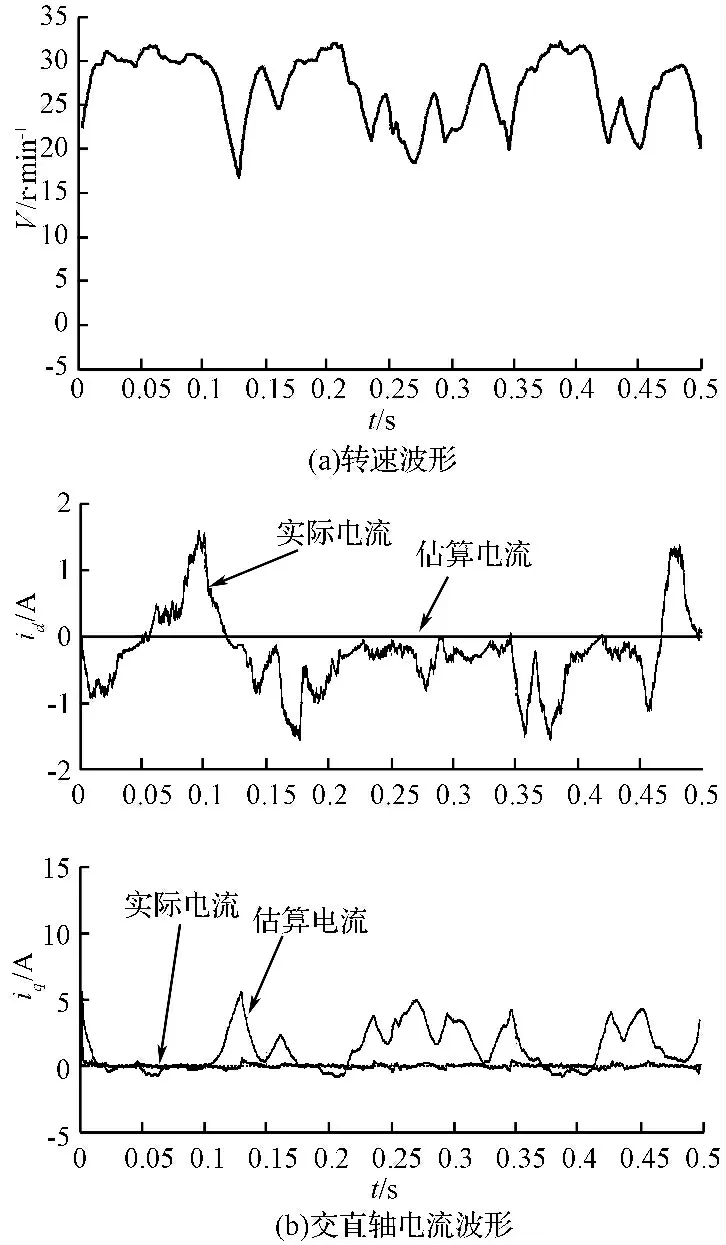
图7 系统在给定转速30 r/min 运行时的仿真波形

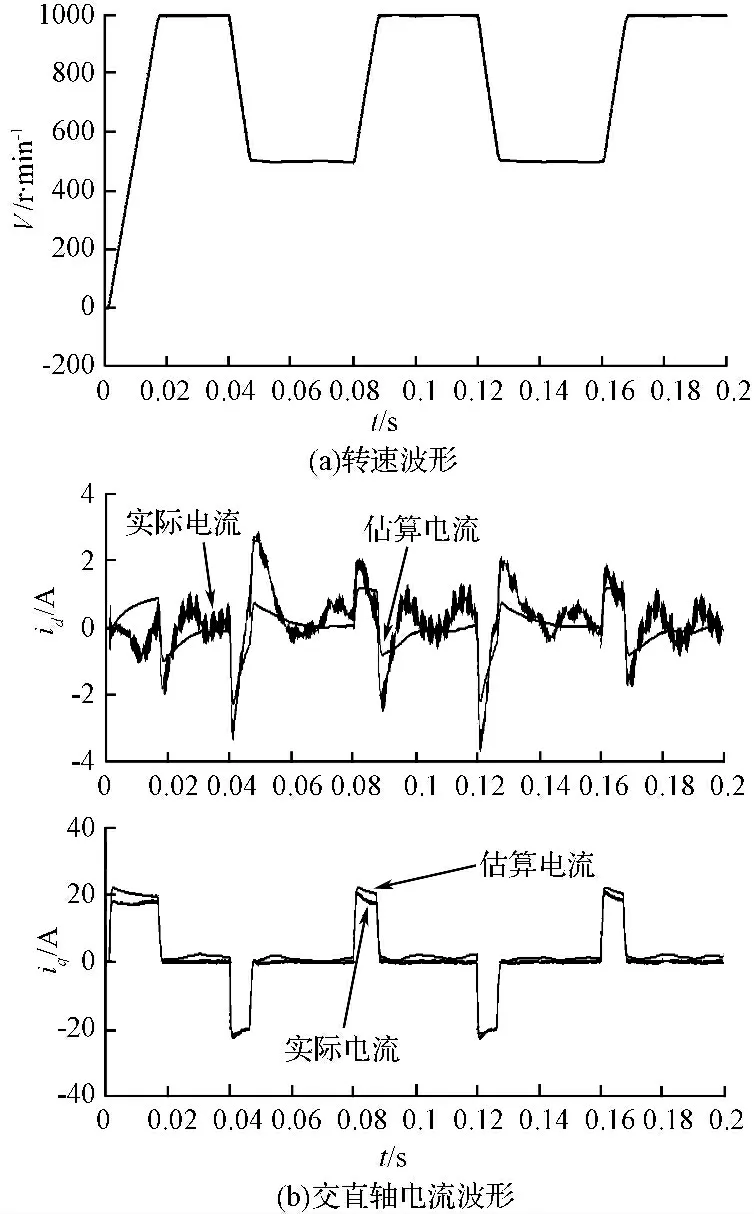
图8 系统动态运行时的仿真波形

从以上分析可知，基于相电流重构的控制系统速度性能总体较为出色，相电流重构算法的电流估算精度较高。但在低速时电流估算性能相对较差，施加负载会提高估算精度。

6 结束语

本研究提出了一种基于相电流算法重构的无电流传感器的永磁同步电机速度伺服系统方案，建立了各组成部分的仿真模型，进行了系统的性能分析。

从分析结果可知，相电流重构的控制系统速度性能总体较为出色，相电流重构算法的电流估算精度较高。但在低速时电流估算性能相对较差，适合中、高速运行场合应用。

［1］鲁文其，胡育文，杜栩扬，等．永磁同步电机新型滑模观测器无传感器矢量控制调速系统研究［J］．中国电机工程学报，2010，33(30):78-83．

［2］鲁文其，黄文新，胡育文．永磁同步电动机新型滑模观测器无传感器控制［J］． 控制理论与应用，2009，26(4):429-432．

［3］TOMONOBU S，TSUYOSHI S，KATSUMI U． Vector Control of Permanent Magnet Synchronous Motors Without Position and Speed Sensors［C］//Power Electronics Specialists Conference，26th Annual IEEE． Atlanta，GA，USA:IEEE，1995:759-765．

［4］BADO A，BOLOGNANI S，ZIGLIITTO M． Effective Estimation of Speed and Rotor Position of a pm Synchronous Motor Drive by a KALMAN Filtering Technique［C］// Power Electronics Specialists Conference，23rd Annual IEEE． Toledo，Spain:IEEE，1992:951-957．

［5］DHAOUADI R，MOHAN N． Design and implementation of an ex-tended KALMAN filter for the state estimation of a permanent magnet synchronous motor［J］． IEEE Transactions on Power Electronics，1991，6(3):491-497．

［6］WU Chun-hua，CHEN Guo-cheng，SUN Cheng-bo． Sliding mode observer for sensorless vector control of PMSM［J］．Advanced Technology of Electrical Engineering and Energy，2006，25(2):1-3，51．

［7］SUN Yi-biao，GUO Qing-ding． Feedback linearization speedtracking control of linear servo system based on sliding mode observer control［J］．Control Theory ＆ Applications，2004，21(3):391-394．

［8］WANG Jia-jun，WANG Jiang，XU Zhen-lin． Variable structure control of PMSM system based on inverter dead-time［J］．Control Theory ＆ Applications，2002，19(4):579-582．

［9］沈安文，杨薇薇，郑定富．无电流传感器的永磁同步电机伺服系统［J］．电气传动，2005，35(10):20-21．

［10］MORIMOTO S，SSNADA M，TAKEDA Y． High performance current sensorless drive for PMSM and synRM with only low resolution position sensor［J］．IEEE Transaetions on Industry Applications，2003，39(3):792-801．

［11］李新兵，张继勇．高性能永磁同步电机交流伺服系统的研究［J］．机电工程，2005，22(4):30-31．

［12］钱 昊，赵荣祥．基于DSP 的永磁同步电机矢量控制系统［J］．机电工程，2005，23(5):12-15．

［13］陈 高，杨家强． 基于TMS320F28335 的永磁同步电机数字化矢量控制器设计［J］． 机电工程，2011，28(9):1090-1094．

［14］吴家彪，马钧华．伺服系统永磁同步电机参数辨识策略［J］．轻工机械，2013，31(6):45-50．

［15］王子涛，王家军，郭 超．基于TMS320LF2812 的永磁同步交流伺服系统［J］．机电工程，2012，29(9):1050-1054．