公共自行车多目标动态调度建模与算法研究*

吴满金 ，董红召* ，刘冬旭 ，陈 宁

(1．浙江工业大学智能交通系统联合研究所，浙江杭州310014;2．浙江科技学院机械与汽车工程学院，浙江杭州310023)

0 引 言

公共自行车作为“低碳排放”［1］的中短途绿色交通形式，在全世界越来越受到推崇［2-3］。随着公共自行车系统(PBS)规模逐渐增大，租赁需求不平衡及部分自助服务点位置不合理等原因导致了自行车“租还难”现象的产生，公共自行车调度问题随之而来。目前，调度模型方面的研究主要围绕着不同目标及约束条件而展开。董红召［4］、Ravi［5］等人以公共自行车用户满意度为优化目标建立了模型。Caggiania 等［6］建立了以车辆调度成本最低为优化目标的自行车动态再分配仿真模型。Kloimullner 等［7］提出了使整体自行车调度数量最少的调度优化模型。Pfrommer 等［8］通过对公共自行车服务点设定动态变化的租车价格建立了再平衡调度模型。上述研究虽然在公共自行车调度方面取得了一定进展，但考虑的约束条件较少，且都仅对单个优化目标进行建模及求解，而实际调度过程中，往往涉及到用户满意度、企业调度成本等诸多影响因素。因此，为有效缓解公共自行车系统的“租还车难”问题，平衡公共自行车在时间和空间上的分布，提高公共自行车的利用率，有必要对统筹用户满意度及企业调度成本的公共自行车调度问题进行研究。

本研究针对公共自行车系统自行车时空分布不均衡的问题，对公共自行车调度过程中自助服务点调度优先级、动态需求特性、服务时间窗等进行研究。

1 PBS 多目标优化调度模型的建立

1．1 服务点调度请求

目前，公共自行车系统“租还车难”的问题比较凸显，需调度的服务点较多，而调度的力量相对有限，仅能对一定数量的服务点进行调度。因此，本研究根据公共自行车系统服务点车锁比(服务点自行车数量与锁桩数量的比值)，对服务点进行调度优先等级划分，并设定调度请求判断条件。

(1)一级服务窗口A+，即优先进行调度的服务点集合。本研究对车锁比满足α≤0．1 或α≥0．9 的服务点进行优先调度，并将其放入到服务窗口A+中。

(2)二级服务窗口A－，即准备进行调度的服务点集合。当服务点车锁比满足α≤0．2 或α≥0．8 时，本研究将其放入服务窗口A－中，准备接受调度车辆的调度。在保证能够对A+窗口的服务点优先调度的情况下，再对A－窗口的服务点进行调度，同时，尽量不增加调度车辆的调度路径。

(3)三级服务窗口B，即尚未有调度需求的服务点和已经接受过调度的服务点集合，该集合中的服务点不接受调度请求。

实际运用过程中，调度优先级的划分(车锁比的设定)可根据实际情况而定。

1．2 服务点租赁需求量的确定

假设编号为i 的任意服务点可容纳的公共自行车数量为Ei，在t 时刻自行车数量为qi(t)，车锁比值为αi(t)，设定能正常提供服务的最小及最大车锁比分别为αmin，αmax。当αi(t)＜αmin时，服务点为调入需求量:

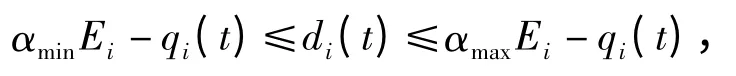
取其平均值:

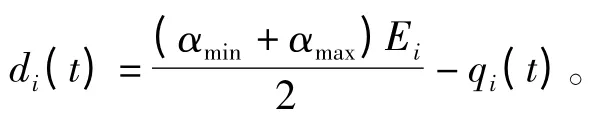
同理，当αi(t)＞αmax时，为调出需求量:

总结如下:

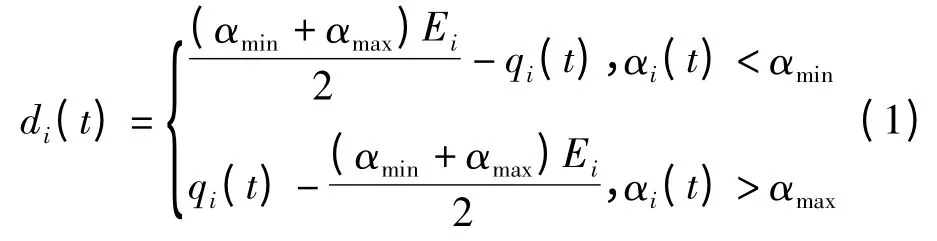
1．3 服务点调度时间窗的确定

服务点间的行驶时间是制定公共自行车调度计划的重要依据。假设服务点i－1 到服务点i 的距离为Si，调度车平均行驶速度为vave，在服务点i－1 到i 之间的行驶时间为Si/vave，则从调度中心出发到第i 个服务点所需的总时间为。而在实际调度过程中，道路交通状况的动态变化导致调度车辆在服务点间的行驶时间也随之动态变化，因此:

式中:vh—调度车高峰时段平均行驶速度，va—平峰时段平均速度。

最终得到服务点调度时间窗约束条为:

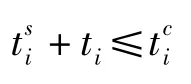
1．4 动态调度模型的建立

模型参数的含义如下:

Q 表示调度车的最大运载量;

di(t)表示t 时刻，服务点i 需要运进或运出的自行车数量;

Vi+1(t)表示t 时刻，对服务点i 完成调度后，调度车上的自行车数量;

c0表示使用每辆车的固定成本;

ε 表示车辆运行单位距离所需的成本;

ρi表示服务点i 的权重值;

Wi表示服务点i 的锁桩周转率。

公共自行车系统需要统筹考虑用户需求和调度成本，本研究建立了以用户满意度最大、调度成本最低为多优化目标的特征函数，具体如下:

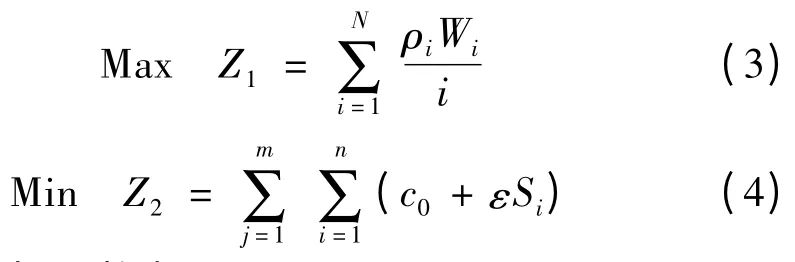
综合目标函数为:

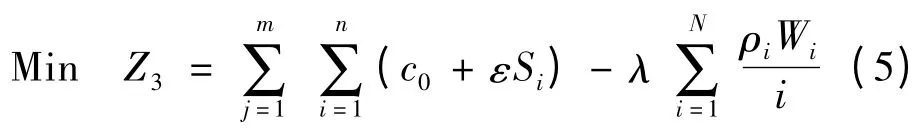
式(3)表示用户满意度，通过服务点周转率体现。周转率高则表明自行车的利用率高，说明能更好地为用户提供服务，使用户对自行车系统的满意度更高。其中:ρi—根据服务点类型取值，一般情况下中心服务点ρi取1．5，普通服务点ρi为1．0;n—调度计划中，服务点接受调度的序号，即表示该服务点为第n 个接受调度的服务点。可以看出对周转率大，权重值高的服务点进行优先调度，调度计划整体周转率Z1就越高，即满意度越高。式(4)表示车辆使用固定成本及行驶成本。式(5)表示多目标综合成本，λ 为变换因子［9］，λ=K0Knc0，其中:K0—常数，决定了对用户满意度的注重程度，根据经验设定;Kn—受调度的服务点数量。

约束条件为:s．t．

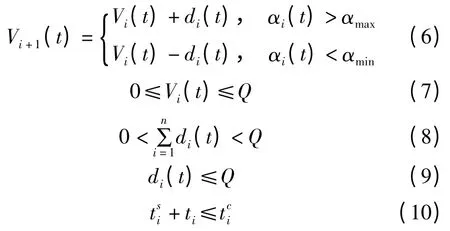
式(6)表示调度完服务点i 后，调度车上的自行车数量;式(7)表示调度车在任何时刻都不超过最大运载量;式(8)表示各服务点调入与调出总量不超过车辆的最大运载量;式(9)表示单个服务点需求量均不超过车辆的最大运载量。式(10)为车辆服务时间的约束条件。

2 算法设计

智能优化算法主要包括禁忌搜索算法［10］、遗传算法［11］、蚁群算法［12］及模拟退火算法［13］等，以上算法单独使用时，都存在一定的局限性，大多数学者采用混合智能算法［14-16］以弥补算法本身的缺陷。禁忌搜索算法能够跳出局部最优，爬山性能较好，但邻域构造简单，一定程度上削弱了算法的搜索能力。相反，遗传算法虽然有着易早熟的缺点，但算子选择、交叉、变异能够产生新的种群，可有效增加邻域的多样性，两者有着较好的互补性。考虑公共自行车调度的各种约束，本研究采用禁忌搜索算法与遗传算法相结合的混合算法求解公共自行车调度模型，得到调度车辆最优的行驶路线，满足其社会效益及经济效益的需求，具体流程如图1 所示。

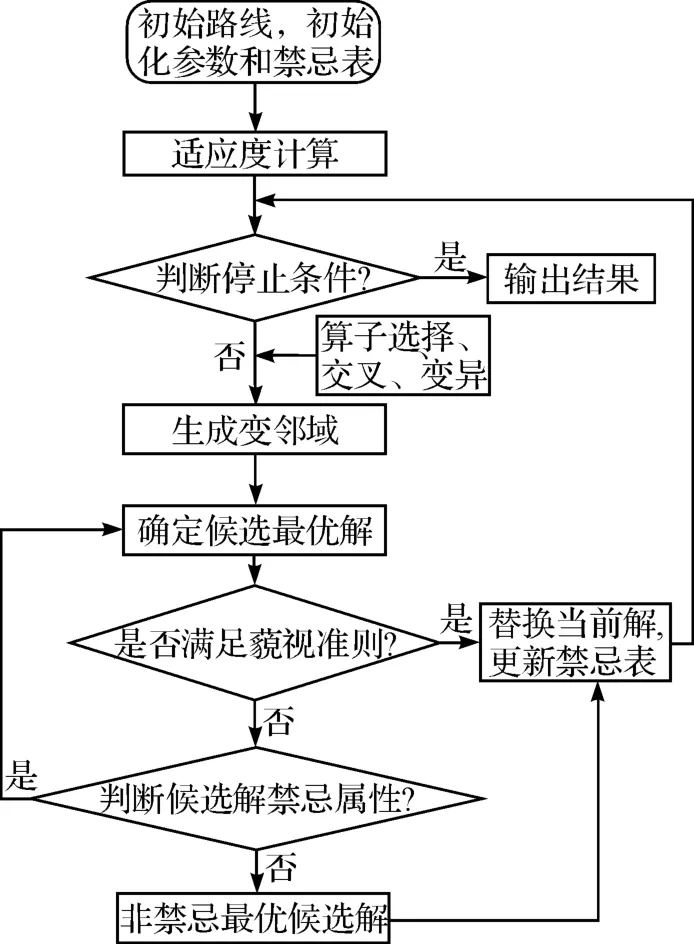
图1 混合算法流程图

2．1 调度初始路线获取与适应度函数

本研究对公共自行车初始调度路线采用双层编码方式。第一层序列代表调度车经过的n 个服务点的一种调度路径;根据调度车辆的容量约束条件，将调度路径分割成多条有效的子路径，这些子路径直接构成第二层序列。本研究选取公共自行车调度模型中的综合目标函数式(5)为混合算法的适应度函数。

2．2 变邻域生成

(1)算子选择。本研究采用精英保留策略与轮盘赌相结合的方法进行算子选择。选取群体中10%的优秀个体保留至下一代，该部分优秀个体不参与交叉变异。剩余90%的个体采用轮盘赌选择方法进入下一代参与交叉和变异的操作。

(2)交叉算子。交叉算子可有效避免某些算子存在的“早熟收敛”，在算法中起着关键作用。采用双交叉点随机组合的方法，算子交叉示意图如图2 所示。

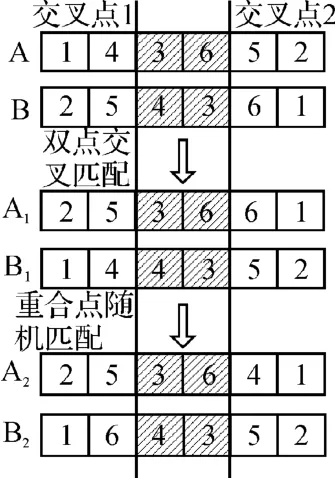
图2 算子交叉示意图

(3)算子变异。算子变异改变的是某一路径上某个服务点的顺序，这里采用2-Opt 算法进行算子变异操作。对某一条调度路线任选两个不相邻的路段进行交换，如果交换后的目标值有所提高，并且满足容量约束，则更新该路线，否则保持原路线不变。

2．3 禁忌表与藐视准则

禁忌表用于存放禁忌对象，表示在搜索过程中被禁忌的操作，即产生的新解若为禁忌对象，则不能替换当前解，以避免陷入局部最优。藐视准则是为了避免遗失优良解，而让部分禁忌对象可以被重新选择，即候选解集中的某个解优于历史最优解时，不考虑该解是否属于禁忌对象，直接替换当前解。

3 实验与分析

3．1 实验方案与数据

本研究选取杭州市滨江某区域的公共自行车系统为调度研究对象，该区域内共有一个调度中心M0 和62 个公共自行车系统服务点，选取9 个满足一级服务窗条件的服务点作为实验对象，其中相关租赁需求数据如表1 所示。设定服务点需要运出自行车时di(t)＞0，运入自行车时di(t)＜0。实际每辆调度车最大可装载自行车的数量为75 辆，行驶里程成本为2 元/km，调度车平均行驶速度为36 km/h，各服务点以及服务点与调度中心之间的距离如表2 所示。根据以往调度经验设定调度人员上架或下架一辆自行车需20 s时间，则调度车在服务点的调度停留时长为di(t)/3 min，转化为行驶距离后为0．2di(t)km，调度一轮的固定成本c0为80 元，用户满意度变换因子为0．36 c0。

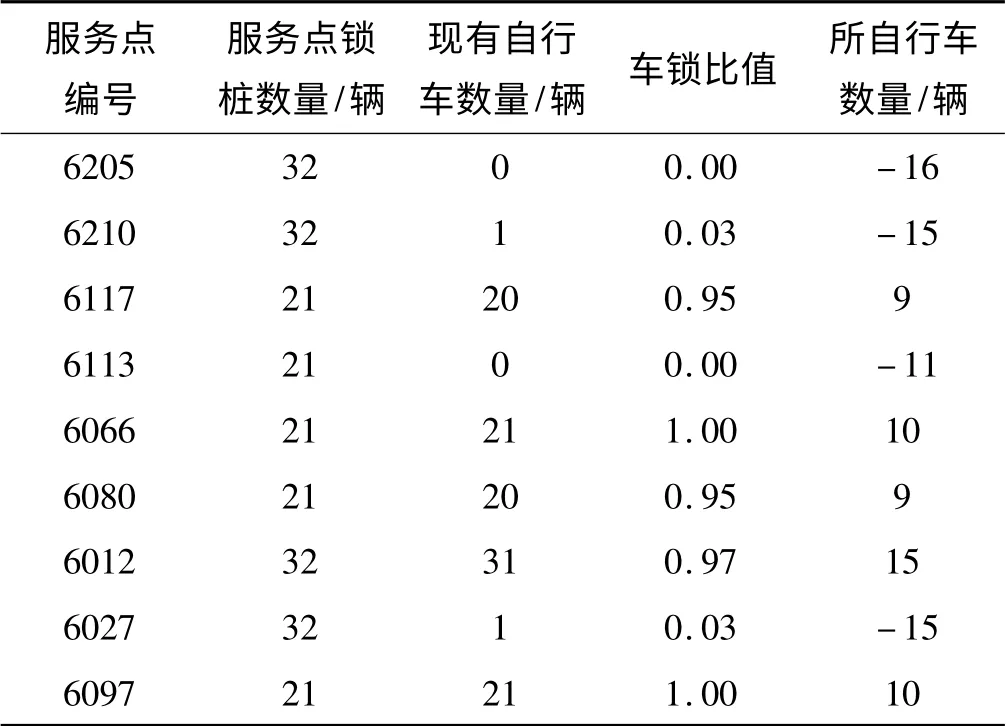
表1 服务点租赁需求信息数据表

3．2 结果分析

本研究根据表1，表2 所示实验数据，通过禁忌遗传混合算法获取公共自行车系统的调度计划。在实验测试结果过程中，一共进行了20 次的迭代次数为200的实验，得到了8 次表现相同的最优调度方案，最优解如表3 所示。

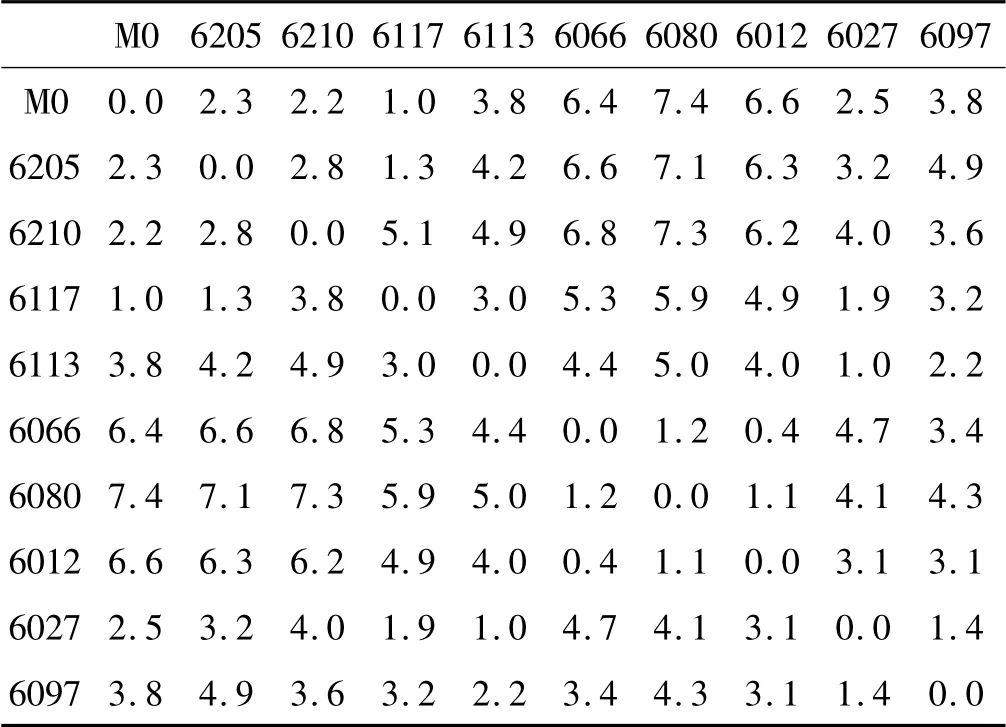
表2 各服务点以及服务点与调度中心之间的距离

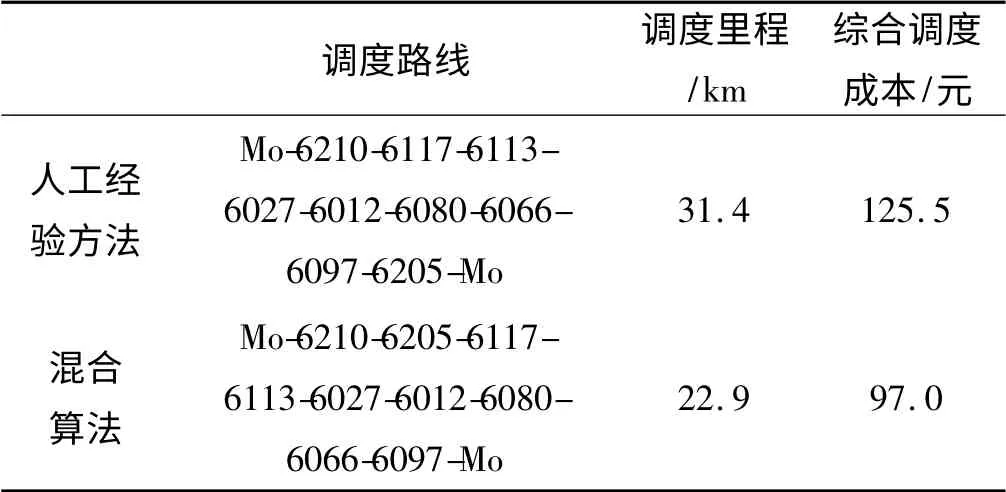
表3 禁忌遗传混合算法的最优解

从表3 中可以得到，由混合算法优化得到的调度路线总长度仅为22．9 km，比经验路线的路径长度减少了8．5 km，约占27．1%;同时优化后的路线对重要服务点(6210，6205)进行了优先调度，尽可能的提高了用户的满意度。优化路线的综合调度成本为97 元(非实际成本仅作参考)，比经验路线的综合调度成本节约了28．5 元，约为优化前的22．7%。对应的路线如图3 所示，虚线为调度车根据经验路线进行调度的实际行车轨迹，由车载GPS 定位系统得到;黑色路线为优化后的调度路线。从图3 中可看出，经验调度时，调度车在部分服务点间的行驶路线非最短距离路线，而是进行了不必要的绕行。而优化后路线在合理安排服务点接受调度顺序的同时，调度车在两服务点间的行驶路线为最短距离路线，大大降低了调度成本。

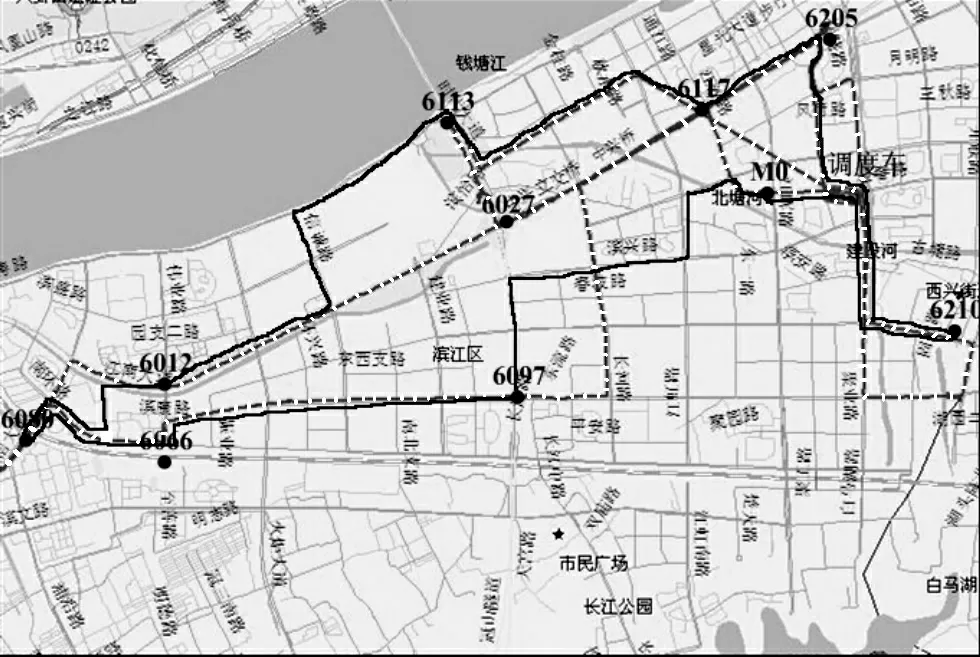
图3 调度车行驶路线图

4 结束语

通过分析公共自行车系统调度问题的特性，笔者建立了以调度成本最低与用户满意度最高为优化目标的公共自行车系统动态调度模型，利用禁忌遗传混合调度算法对公共自行车系统动态调度模型进行了求解，实验结果基本可行。

该算法在保证用户满意度基础上，减少了调度车辆的行驶距离，解决了以往单目标调度优化而导致的系统整体优化结果缺失的问题，对公共自行车系统调度工作具有重要指导意义。此外，调度计划的质量在一定程度上还依赖于服务点潜在用户需求量的精确估算，这需要更进一步的探索。

［1］陈 飞，诸大建．城市低碳竞争力理论与发展模式研究．城市规划学刊［J］．2011(4):15-22．

［2］SHAHEEN S A，GUZMAN S，ZHANG H． Bikesharing in europe，the americas，and asia［J］． Transportation Research Record，2010(2143):159-167．

［3］FISHMAN E，WASHINGTON S，HAWORTH N，et al．Factors influencing bike share membership:an analysis of melbourne and brisbane［J］． Transportation Research Part A，2015(71):17-30．

［4］董红召，赵敬洋．公共慢行系统的动态调度建模与滚动时域调度算法研究［J］．公路工程，2009，34(6):68-75．

［5］RAVIV T，TZUR M，FORMA I A． Static repositioning in a bike-sharing system:models and solution approaches［J］．EURO Journal on Transportation and Logistics，2013，2(3):187-229．

［6］CAGGIANI L，OTTOMANELLI M． A dynamic simulation based model for optimal fleet repositioning in bike-sharing systems［J］． Procedia-Social and Behavioral Sciences，2013(87):203-210．

［7］KLOIMULLNER C，PAPAZEK P，HU B． Balancing bicycle sharing systems:an approach for the dynamic case［J］． Evolutionary Computation in Combinatorial Optimisation，2014(8600):73-84．

［8］PFROMMER J，WARRINGTON J，SCHILDBACH G，et al． Dynamic vehicle redistribution and online price incentives in shared mobility systems［J］． IEEE Transactions on Intelligent Transportation Systems，2014，15(4):1567-1578．

［9］贾永基，王长军．基于满意优化的多目标车辆调度问题模型与算法［J］．东华大学学报，2009，35(3):351-354．

［10］ALESSANDRO C，KNUST S，MEIER D，et al． Tabu search and lower bounds for a combined production-transportation Problem［J］． Computers and Operations Research，2013，40(3):886-900．

［11］MOCKOVA D，RYBICKOVA A． Application of genetic algorithms to vehicle routing problem［J］． Neural Network World，2014，24(1):57-78．

［12］胡天军，程文科．带回程取货的逆向物流车辆路径建模及其蚁群算法［J］． 交通运输系统工程与信息，2010，10(3):110-114．

［13］XIAO Y，ZHAO Q，KAKU I，et al． Variable neighbourhood simulated annealing algorithm for capacitated vehicle routing problems［J］． Engineering Optimization，2014，46(4):562-579．

［14］朱珈楠，陈 勇，鲁建厦．多品种多工艺制造企业车间作业调度的ACA 建模［J］． 轻工机械，2013，31(3):99-103．

［15］余 丽，陆 锋，杨 林．交通网络旅行商路径优化的遗传禁忌搜索算法［J］． 测绘学报，2014，43(11):1197-1203．

［16］GASPERO L D，RENDL A，URLI T． A Hybrid ACO+CP for balancing bicycle sharing systems［J］． Hybrid Metaheuristics，2013(7919):198-212．