10kV配电网串联补偿电容内部故障的诊断方法

陈 璞 ，任 勇 ，陈 可 ，江道灼* ，陈 峰 ，毕仁明

(1．南网贵州供电公司，贵州贵阳市550001;2．浙江大学电气工程学院，浙江杭州310027;3．浙江桂容谐平科技有限责任公司，浙江杭州310030)

0 引 言

电压质量一直是衡量供电质量是否符合标准的一项重要指标。而我国配电网建设相对滞后，局部地区存在网架薄弱、设施老化、线径小、配电变压器数量多问题［1］，尤其是较多线路带有多台大容量的电动机或变化迅速的工业负荷，往往导致线路末端电压低、电压跌落严重的问题。

一般采用随用电器的分散式并联无功补偿的方法解决上述问题［2］。但该方法存在一条配电线路上的安装数量多、维护量大、开关动作频繁、噪声大、响应速度慢的弊端，并且会造成重载时电压低、轻载时电压高。

串联补偿装置的结构和控制相对简单，既可以起到提高稳定极限，增强输送能力，和调节潮流分配等作用，并具有负荷“自适应”电压调节和实时响应的特点［3-6］，相比之下有更好的经济性和发展前景。

固定串联电容器(D-FSC)是其中最常见的串联补偿装置，但是D-FSC 一旦出现电容元件的老化，不仅会造成高压电容器损坏，甚至可能出现鼓肚、群爆等严重的设备事故，给电网安全运行造成影响［7］。

目前电力电容器装置一般采用文献［8］提出的电流(或电压)差动保护等常规安全运行保护措施，需要额外配置电压电流的检测设备，增加了设备成本。文献［9-11］提出的基于电容值的故障诊断判据，通过检测电容器两侧的电压和电流，直接计算电容值来判断其损坏情况，此判据未考虑系统含有谐波的情况，导致在系统含有谐波时精度不高，甚至出现误判。

本研究首先分析D-FSC 在辐射状线路中改善电压特性的基本原理，并通过对电力电容器及其所在系统的建模，提出一种判断电容器内部故障的判据方法，考虑系统存在谐波的情况，最后通过仿真验证判据的有效性和可行性。

1 D-FSC 基本原理

辐射状线路中感性负荷用电向量图如图1 所示。线路中当加入串联电容器XC时，如图1 所示。

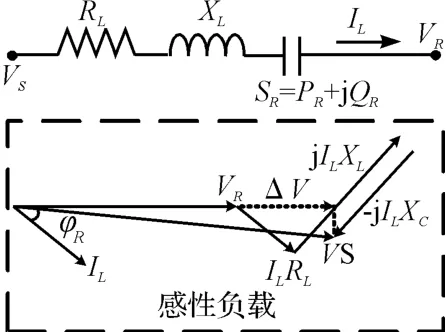
图1 加入D-FSC 时的向量图

此时，由图1 中的向量图可得，线路首末端线电压之差(一般只考虑纵分量):

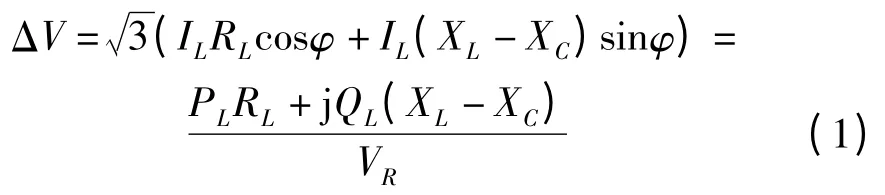
由式(2)可知，D-FSC 在线路中相当于一个电压调节器。它总能产生一个与线路电抗电压相反的电压，其值为:

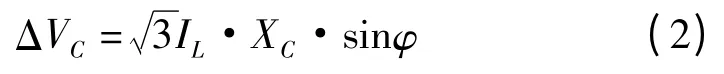
该串联电容器提供的无功补偿容量为:

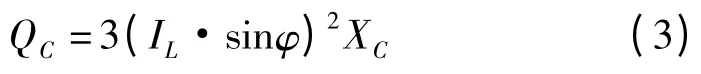
由式(3，4)可知，D-FSC 补偿的电压与线路电流成正比，容量与电流的平方成正比。

当串补装置下游负荷越重，即造成线路首末端电压差越大时，串补补偿的电压就也越大，而当负荷较轻或空载时，线路电流很小，其补偿的电压也随之减小，这是D-FSC 能够“自适应”电压调节的基本原理，也是串补最大的特点和优势。

2 D-FSC 结构及补偿电容内部结构

D-FSC 装置串于配电线路中两个分接点(配变支路与主线的连接点)之间，结构如图2 所示。

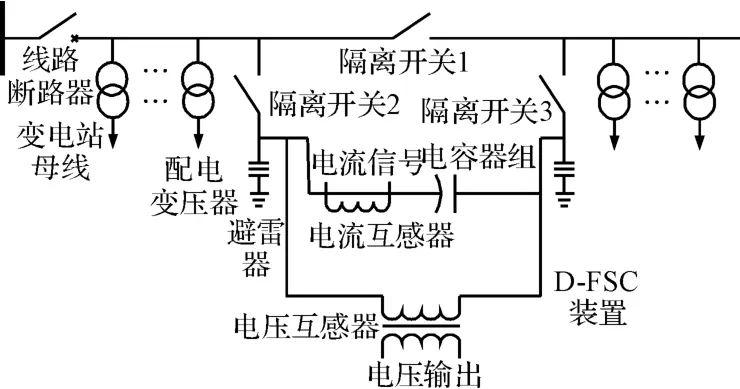
图2 固定串联补偿装置的结构图

串联补偿电容结构如图3 所示。电容器中电容由多个内部小电容和内部电阻的并联，其中每个小电容都串联一根内熔丝，一旦内部小电容发生故障时，与其串联的内熔丝迅速熔断，从而隔离故障元件，而其余小电容则可以继续运行。

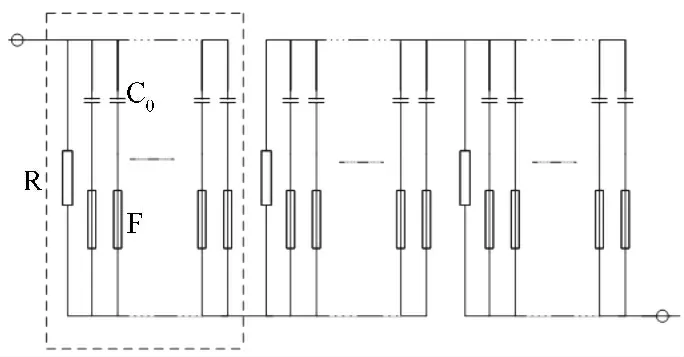
图3 电容器内部结构

3 电容器故障建模分析

3．1 电力电容器建模

大容量电力电容器一般由数十个甚至上百个小电容串并联构成。以常用型号BAM11/√3-334-1W 电容器为例，由36 个电容元件12 并3 串构成，结构图如图2 所示。并联的电阻很大，电容器的有功损耗很小，其电阻值可以忽略。电容器容值为4C0=26．359 2 μF。对其进行简化后的内部结构如图3 所示。则一个电容器的电容值C 可以通过下式计算:

式中:I—流过电容器的电流有效值，U—电容器电压有效值，ω—角频率。

若内部小电容发生不同损坏，其电容值可以通过如下计算:

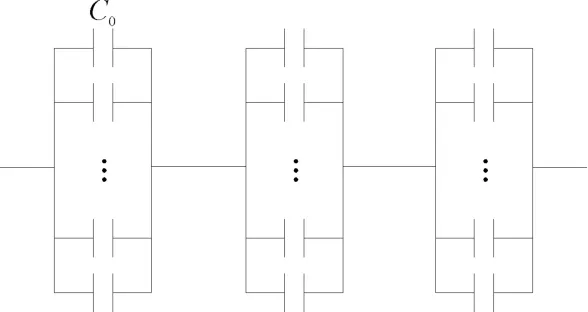
图4 简化后的电容器内部结构图

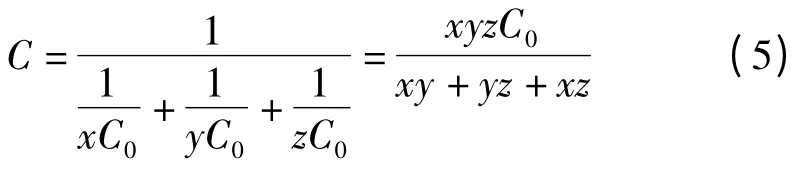
式中:C0—内部单个小电容容值;x，y，z—电容器3 个并联组中对应正常工作的小电容个数。

因此，电容器容值的相对变化百分比可以表示为:

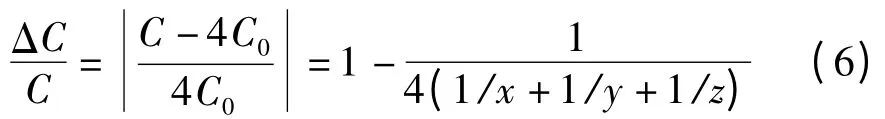
例如，当一个电容器发生两只小电容损坏时，有以下共2 种情况:

(1)两只小电容分别损坏在2 个并联组中，即x，y，z 中其中一个为12，其余两个是11，例如(x，y，z)=(11，11，12)，则:

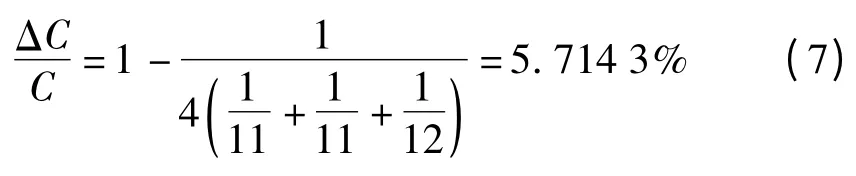
(2)两只小电容损坏在同一个并联组中，即x，y，z中其中一个为10，其他两个是12，例如(x，y，z)=(10，12，12)，则:

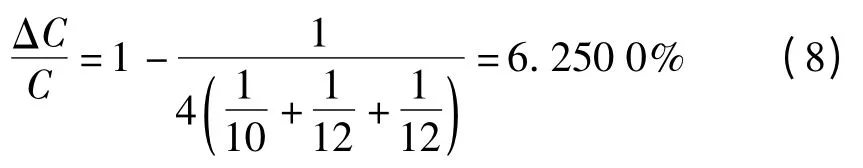
因此，当发生两只内部小电容损坏时，电容器容值变化百分比通过两者取平均可以近似为5．982 2%。同理可以分别求出损坏0、1、3 个小电容时的电容器值相对变化百分比，具体如表1 所示。

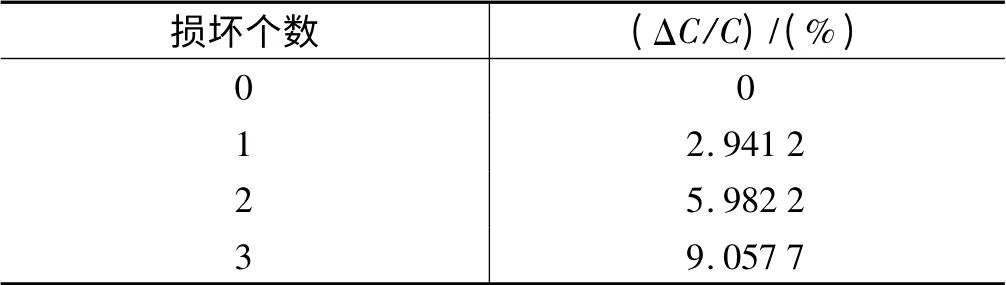
表1 电容器内部故障时容值变化百分比

本研究通过监测电容器电流电压，利用式(5)求得电容器实时电容值，再根据式(6)和式(7)，计算电容器容值变化率，从而诊断电容器故障。由于表1 是理想情况下所得到的容值百分比，实际情况下由于误差的存在，取一定范围进行判断，判据表如表2 所示。

3．2 提高精度的改进判据

一般情况下，系统中常常存在谐波，采用式(5)计算容值忽略了系统谐波的情况，可能出现误诊断，如:

表2 判据表

电容器完好无损，容值4C0为26．359 2 μF。电容器上通过的基波电压有效值为1 kV，假设系统中存在谐波且3、5、7、11 次谐波幅值分别为10%、5%、3%和2%。通过检测电容电压有效值U 和电容电流有效值I，经过式(5)计算容值C 为29．266 μF，电容器容值的相对变化百分比为9．932%，判断损坏3 个电容，出现误诊断。操作人员根据原有判据切断D-FSC，就会造成时间、资源上不必要的浪费。

因此，在考虑谐波特性的情况下，对检测到的电压和电流进行FFT 展开提取电压和电流的基波和各次谐波分别为U(1)、U(3)、U(5)…I(1)、I(3)、I(5)…。因此各次谐波下电容器的容值C(i)为:

式中:i—谐波次数。

理论上，基波和各次谐波下计算得到的电容器容值相同，但是在实际中存在差别，因此电容器容值的估算值根据基波和各次谐波在电路中所含的比例可以通过式(10)进行估算:

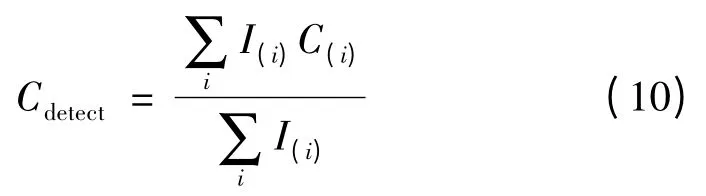
得到电容器的估算之后，得到下式:

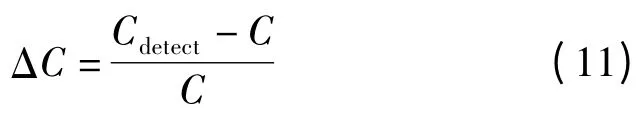
根据式(10～11)的值修正容值变化百分比，然后根据表2 进行故障判断。

4 仿真分析

从电容器的模型构建中可以发现，常规判据和改进判据在无谐波影响情况下得出的结果一致(改进判据在无谐波影响下相当于只有基波分量)，但是在系统存在谐波时会得到不同结果，下面将从仿真中验证新型判据。

4．1 内部故障仿真

当系统存在谐波，电容器组没有损坏时，电容上电压电流谐波含量如图5、图6 所示。

图5 无电容损坏时的电容电压

图6 无电容损坏时的电容电流

其基波电压有效值U(1)为240．667 V，基波电流有效值I(1)为1．991 2 A，五次谐波U(5)为10．329 V，I(5)为0．438 1 A，七次谐波U(7)为4．616 V，I(7)为0．255 1 A，用常规判据得到电容C 为27．146 9 μF，容值变化百分比2．902%，改进判据容值C 为26．380 2 μF，容值变化百分比0．08%。根据判据表，在常规判据下，因为谐波影响判断有1 个电容发生损坏，跟实际情况相违。而改进判据不会受其影响。

当两只小电容损坏在同一个并联组中，其他电容没有损坏时，电容上电压电流谐波含量如图7、图8 所示。

图7 电容损坏时的电容电压

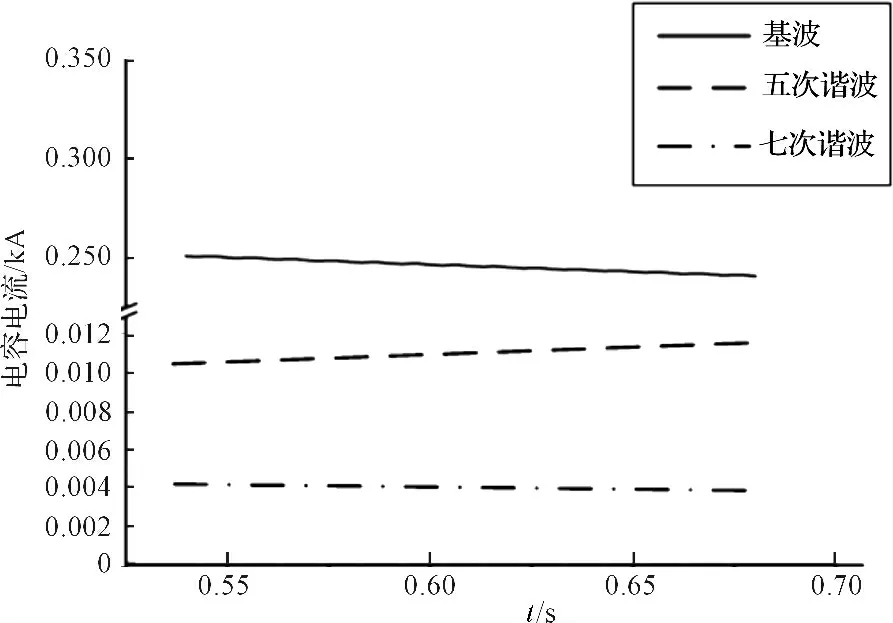
图8 电容损坏时的电容电压

其基波电压有效值U(1)为246．724 V，基波电流有效值I(1)为1．915 A，五次谐波U(5)为11．030 V，I(5)为0．438 A，七次谐波U(7)为4．065 V，I(7)为0．226 A，用常规判据得到电容C 为25．487 μF，容值变化百分比3．421%，判断仅1 个电容发生故障，再次出现误判断。改进判据容值C 为24． 855 μF，容值变化百分比6．052%，2 个电容发生故障。

4．2 改进判据对比

当实际情况中电容器组小电容发生不同个数损坏时，得到两种判据结果对比如表3 所示。

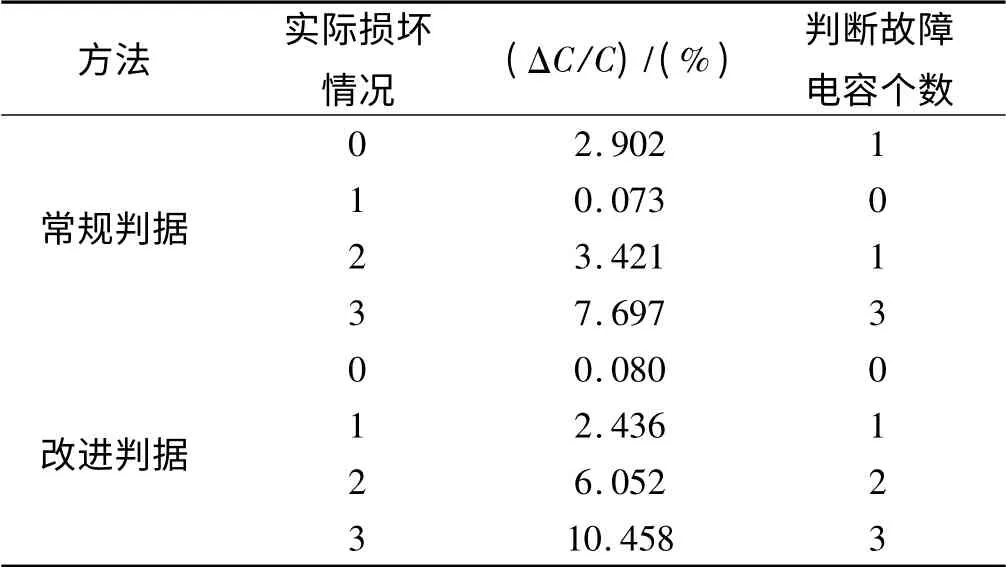
表3 判据对比

表3 中，损坏情况均发生在单个并联组中。从表3 可以看到改进判据较理想，常规判据在没有电容损坏时误判断有内部故障发生，而当有故障发生时又误判断D-FSC 内部电容全部正常，对系统中存在谐波情况下失去了准确性。改进判据则解决了这样的问题，在系统有无谐波时都能很准确地判断故障是否发生，以及电容损坏的个数。

5 结束语

本研究通过分析D-FSC 在辐射状线路中改善电压特性的基本原理，得出了串补装置的“自适应”电压调节特点，并在归纳原有D-FSC 补偿电容诊断方法基础上，提出了一种解决系统谐波影响下的电容器内部故障诊断判据，将其与原有判据进行仿真分析对比。通过对D-FSC 内部故障诊断判据的研究得出，新判据的提出可以有效解决系统谐波的影响，准确判断电容内部故障情况，相比原有判据更具优越性。

［1］戴晓亮，无功补偿技术在配电网中的应用［J］．电网技术，1999，23(6):1-7．

［2］麦敏坚． 探讨改善配网的电压质量［J］． 电力建设，2008(185):139-141．

［3］卓谷颖，江道灼，梁一桥．改善配网电压质量的固定串补技术研究［J］．电力系统保护与控制，2013(8):66-72．

［4］梁一桥，吕佳铭．一种10 kV 配网智能串联补偿装置及其工程应用［J］．电网技术增刊，2015．

［5］MAGOWAN J M． Voltage performance of series capacitors in transmission and distribution lines［J］．The Institution of Electrical Engineers，1957，104(18):505-516．

［6］ROSSO A D，CAÑIZARES C A，DOA V M． A study of TCSC controller design for powersystem stability improvement［J］．IEEE Transactions on Power Systems，2003，18(4):1487-1496．

［7］MISKE S A． Considerations for the application of seriescapacitors to radial power distribution circuits［J］． IEEE Transactions on Power Delivery，2001，16(2):306-318．

［8］黄旭东，电力电容器保护探讨［J］．电力电容器与无功补偿，2009，30(3):48-51．

［9］刘 艳，刘瑞云，陶维亮，等．电力电容器故障检测系统的设计与实现［J］．电气应用，2011，30(12):78-82．

［10］陈福锋，钱国明，宋国兵．串联电容补偿线路行波差动保护的研究［J］．中国电机工程学报，2009，29(28):89-94．

［11］QIAO Lei． Estimated means of reactive power for distributed small hydro stations based on optimal power flow［J］．Electric Power System and Its Automation Journal，2008，20(2):88-93．