基于AB运动控制系统的凸轮曲线研究
杨 钧,高 强
(上海交通大学电子信息与电气工程学院,上海200240)
0 引 言
随着电子技术的突飞猛进,运动控制得到了广泛的应用,设备的运行速度不断在提高,控制精度要求也越来越高。而为了实现这些目标,除了本身器件的硬性指标外,其控制的算法也起着至关重要的作用。传统的方法有使用梯形、指数等,虽然在一定程度上得到了速度的连续性,但是加速度是阶跃性的,并非连续。在柔性要求较高的场合传统也采用7 段S 曲线,7 段曲线保持了加速度曲线的连续性,但是其加速曲线都为线性,曲线平滑度不够导致加加速度是阶跃性的突变,在一定程度上会加快机械磨损速度[1-2]。而梯形、指数曲线的应用在高速运行的过程中经常出现冲击过流等问题,机械损耗也较大,影响使用寿命。
国外在运动控制方面的应用早于国内,在对于运动曲线的优化方面也有不少的研究,通过电子凸轮来实现曲线的运行轨迹以满足速度和精度都要求比较高的应用场合,主要服务的行业在印刷、造纸、烟草等,这些行业现在主流的设备大多采用国外进口。国内在这方面虽然也采用运动控制技术应用于这些领域,但其控制方式都比较简单,没有或很少有曲线算法应用于实际工程之中,所以在关键性能上还是无法达到国外的同等水平。
本研究引入两种凸轮曲线的算法,对于高速的位置定位采用5 次多项式的凸轮轨迹;对于高速的速度定位则采用正余弦修正的凸轮轨迹,借助AB 的控制系统进行硬件和软件的设计,把理论的曲线算法直接应用于工程之中,通过实验结果可验证这两种曲线的合理性。
1 传统凸轮曲线
传统的曲线大多为梯形、指数和7 段S 曲线[3-4],梯形曲线的算法包括3 个阶段:恒加速、匀速、恒减速。
速度和加速曲线如图1(a)所示,速度呈连续线性变化而加速度的变化不是连续的;
指数算法的曲线同样如图1(b)所示,速度和加速度的算法呈现指数形,但在匀速阶段加速度仍存在阶跃跳变的不连续[5-9];
7 段S 曲线如图1(c)所示,可以看出速度的变化可以做到平滑、连续地过渡,加速过程分为7 个阶段呈连续线性变化,但没有平滑过渡导致加加速度产生阶跃性的变化,没有连续性。

图1 传统曲线
速度和加速度曲线的不平滑对电机和机械机构会产生冲击,电机最大输出电流增大,高速下的系统稳定性变弱,加加速度的不连续性又会加大对机械的磨损速度[10-11]。故而为了保证速度和加速度的连续性和平滑性,本研究提出了五次多项式和正余弦修正的两种凸轮曲线。
2 两种凸轮曲线算法
2.1 五次多项式曲线算法
五次多项式的算法由三次演变而来,但三次的加速率在起始阶段有断点的存在,使其无法满足高速的应用环境,五次多项式顾名思义根据其变量的最高次方数来定义,如式(1)所示:

式中:s—实际的位移值;t—时间变量;C0~C5—不同情况下的固定系数。
通过对式(1)求一阶导和二阶导得出式(2)和式(3):

式中:s',s″—速度和加速度。对加速度的求导生成加加速度曲线,设在t =0 启动的时刻初始位移、速度和加速度都为0,其对应的曲线如图2 所示。

图2 五次多项式曲线
位移总行程记为S,对应t 的总行程时间为T,又因为行程结束时的末速度和末加速度回归为零,可以得到以下方程组:

通过计算可以得出式(5):

从而得到五次多项式的凸轮曲线公式(6):

由得到的公式可知,在已知给定的总时长和需要走的总行程后,就可以确定时间和位移的函数关系,整个过程的加速度和加加速度不仅连续而且其本身也是多项式函数,曲线各点实现了平滑性过度。
在系统最大允许加速度方面,传统的曲线如梯形运行因为其特性是前后加减速中间匀速,故而最大加速度是在起始和结束段,其能达到的最大值是为在系统总惯量下伺服电机以给出100%额定转矩启动时电机得到的加速度值,而五次多项式曲线的加速度曲线是连续性而非阶跃性的跳变,故而其最大加速度必然小于传统曲线运行产生的最大加速度。由于电机输出的扭矩取决于系统惯量和加速度的乘积,惯量保持不变,这样系统相比于传统的曲线运行所需的扭矩和电流更小。
因为五次多项式是在初速V0和初加速A0都为零的条件下,位移-时间的函数关系仅取决于总行程和总时长;在V0或A0不为零的情况下,曲线还受这两个因素耦合,在实际工程中该凸轮曲线的算法适用于由零速到零速的位置定位场合。
2.2 正余弦修正曲线算法
正余弦修正曲线是在摆线运动的基础上修正而来的,普通的摆线曲线如图3 所示。其加速度α 幅值较大导致电机的输出力矩T = J·α 上升(J 为系统惯量),且加速度变化率高影响系统稳定性和使用寿命。
正余弦修正曲线如图4 所示,对加速段分为了三段组合,设横轴总时长为T,总行程为S,第一段曲线为(0-1/8)T,第二段从(1/8-7/8)T,第三段为(7/8-1)T,每一段的时间t 和位移s 的函数关系见式(7):
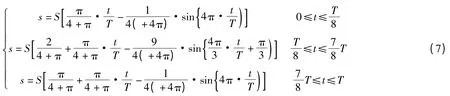

图3 摆线运动曲线

图4 正余弦修正曲线
对应的各阶段的速度与时间的函数关系见式(8),对应的加速度和时间的函数关系见式(9):

由式(7)可以得出当在t =T/2 处时,速度达到最大值V1,加速度恢复到零,设初速为V0,得到式(10):

本研究得出最大速和给定的初速之差只和总行程和总时长相关,此时的位移由式(7)得出也恰好在S/2处,所以当要求速度在规定的时间或是总行程之内达到指定速度的加速场合之下,可以采用正余弦修正曲线的前半段作为运行轨迹;当要求减速应用的场合下则选用曲线的后半段。两种速度定位场合的应用下利用正弦修正曲线的特性保证其加速度和加加速度的连续性和平滑性[12]。
3 实验设计
针对两种凸轮曲线的应用效果,本研究设计了基于AB 运动控制系统的硬件架构和软件程序,把两种曲线直接应用于伺服的控制之中,并进行了测试记录。
3.1 硬件设计
实验的CPU 控制器选用AB 的集成运动控制功能的中型控制器,型号选用1769-L18ERM,该款控制器带有双口以太网,支持CIPmotion 即以太网控制的伺服运动系统,可以带两个物理伺服轴,程序容量最高可支持到512 KB。伺服驱动器选用AB 的Kinetix5500系列,选用两个相同型号2198-H003-ERS 的驱动器作为实验,电机型号选用VPL-A0631M,此电机采用单电缆技术,电源和编码器采用同一根电缆接入到伺服驱动器之中,电机支持的额定转速是7 200 r/min,额定扭矩为0.46 N·m,峰值扭矩可达1.33 N·m[13-14]。硬件系统如图5 所示。

图5 硬件架构图
3.2 程序设计
编程软件在AB 的logix5000 环境下进行组态编程的设计,标准程序和运行控制程序都可以在这款软件下完成。该软件支持梯形、顺序、功能块和语句表的编程语言。
程序设计的流程框图如图6 所示。

图6 程序设计流程图
主程序设计功能主要负责对凸轮曲线计算的程序调用、物理轴运行指令调用以及紧急停止和复位的相关功能。对于曲线在程序中的设计,因为考虑到物理轴的轨迹为凸轮曲线,本研究设计成master 和slave 的主从轴的位置关系来规划曲线,master 作为主轴采用虚拟轴的方式始终做匀速运行,对应曲线算法中的时间横轴,程序设计把总轨迹分成一百个单位以数组的形式让控制器执行,点与点采用程序中cubic 弧线的方法连接。
对于五次多项式预先定义好主轴和从轴的总行程变量及初始位置,本研究把先前计算好的系数C0-C5编入程序当中,程序执行计算把主从轴每一个单位对应点填入数组之中,其形式为cam[x].master 和cam[x]. slave,x 为数组单位序列,在1 s 内位置由零位移动到6 000°(定义电机一圈对应100°)设计的程序描点曲线如图7 所示,对应计算出的多项式系数如图中所示。
C0=C1=C2=0,C3=6 ×10-5,
C4=-9 ×10-8,C5=3.6 ×10-11

图7 五次多项式曲线程序描点图
对于正余弦修正曲线除了预先定义主从轴的初始值变量以外,还需要定位初始速度和末速度的变量,用以服务速度定位功能,本研究在程序设计轨迹规划时对三段总行程进行统一设计,根据逻辑判断指令要求如果是加速情况,则选用曲线的前半段存入主从数组中作为执行轨迹,如果是减速情况,则选用曲线的后半段存入主从数组中作为执行轨迹,在1 s 内加速到90 r/s 的速度定位设计的程序描点曲线如图8 所示,其对应的计算曲线公式如式(11)所示:


图8 正余弦修正曲线程序描点图
从图8 中可以看出在程序中规划出来的曲线其加速从零开始又由零结束,系统冲击变小,并且可以看到加速度和加加速度的曲线都是平滑过渡,系统运行的稳定性加强。
最后,本研究通过软件中凸轮指令MAPC 来运行物理轴,同时在程序中增加主从轴数组清空程序,当根据变量的不同重新规划曲线轨迹前,对之前的曲线进行清空。
4 测试结果及分析
为了验证两种曲线执行的平滑性,本研究在空载的情况下分别进行了高速位置定位和速度定位的两种测试,每种测试下通过对物理轴1 采用传统梯形曲线的定位方式和对物理轴2 采用规划的曲线定位方式进行比较,记录运行过程中伺服电机速度和电流变化趋势。
第一个测试使伺服轴从位置0 在1 s 内移动到位置6 000(对应电机60 圈处),得到两个测试结果如图9、图10 所示。

图9 梯形曲线位置定位

图10 五次曲线位置定位
图9 显示电机在加速和减速过程中有阶跃的冲击,电机电流的最大值达到额定的28%,图10 显示整个的定位过程中电机的电流始终保持连续性,其电流最大值在24%。
第2 个测试使伺服轴由速度0 在1 s 内加速到5 400 r/min,之后保持匀速,得到如下两个测试如结果图11、图12 所示。

图11 梯形曲线速度定位速度、电流采集

图12 正余弦修正曲线速度定位速度、电流采集
如图11 所示,在定速过程中电机电流阶跃性变化,其电流最大值达到额定的20%,如图12 所示,电流变化平滑,其最大电流值为14%。
由两个测试结果可见,根据五次多项式和正余弦修正曲线轨迹运行的伺服轴其扭矩的波动幅值小于传统的梯形曲线,系统冲击变小,并且平滑度也更优于梯形曲线运行的伺服轴。
5 结束语
当前,为了提高生产效率,设备速度被不断提升,但同时又需要保证高精度、高稳定性的要求,传统的曲线轨迹逐渐无法满足这些要求。
本研究通过引入两种不同的凸轮曲线应用于位置定位和速度定位的两种场合之中,成功实现了运动控制在高速下扭矩波动更小,运行更稳定。相信其在汽车、轮胎、机器人、包装等制造业会得到越来越多的应用,并且为适应更高的要求,更加优化的凸轮曲线也会应用于工业领域。
[1]张得礼,周来水. 数控运动加工的平滑处理[J]. 航空学报,2006,27(1):125-127.
[2]郭新贵,李从心,阮雪榆.采用线性加速伺服系统的快速准确定位方法[J].机械工程学报,2003,39(7):74-77.
[3]郑中谦,王兴飞,李 松,等.基于加减速时间控制的S 形速度规划新算法研究[J]. 机电工程,2014,31(4):425-426.
[4]杨 超,张冬泉.基于S 曲线的步进电机减速的控制[J].机电工程,2011,28(7):813-815.
[5]许文斌,洪小丽.CAK3665 数控车床进给伺服系统的建模及仿真研究[J].机电一体化,2014,5(10):33-34.
[6]张 钊,陈 涛,周 勇.永磁同步电机伺服控制系统建模与仿真[J].兵工自动化,2014(4):79-82.
[7]任国华.移动机器人轨迹跟踪与运动控制[J].机械设计与制造,2014,54(3):223-225.
[8]于 蓬,张为春,裴宝浩,等.抢险机器人手臂机液耦合仿真分析[J].液压气动与密封,2011(6):29-33.
[9]赖厚安.基于运动仿真的双层凸轮曲线设计与分析[J].机械工程师,2014,72(5):98-100.
[10]邵世权,刘 霞.凸轮轮廓曲线方程形式的探讨与研究[J].机械研究与应用,2014,34(3):136-137.
[11]王云飞,郎需林,张承瑞,等.高速并联机械手最优加减速控制算法研究[J]. 机械设计与制造,2014,59(11):628-629.
[12]ROTHBART H A,EMERITUS D. CAM DESIGN HANDBOOK. Charpter3:Modified Cam Curves [J]. The McGraw-Hill Companies,Inc.,2004,48(7):83-87.
[13]Rockwell Automation Inc. CompactLogix Controllers Specifications Technical Data[M].Milwaukee:Rockwell,2012.
[14]Rockwell Automation Inc. Kinetix5500 servo drive user manual[M].Milwaukee:Rockwell,2012.

