纹理特征对松林郁闭度的判别能力研究
许章华,刘 健,余坤勇
(1.福州大学环境与资源学院,福建福州350116;2.福建省水土流失遥感监测评估与灾害防治重点实验室,福建福州350116;3.福建农林大学3S技术应用研究所,福建福州350002;4.福建省三明学院,福建三明365000)
纹理特征对松林郁闭度的判别能力研究
许章华1,2,刘健3,4,余坤勇3
(1.福州大学环境与资源学院,福建福州350116;2.福建省水土流失遥感监测评估与灾害防治重点实验室,福建福州350116;3.福建农林大学3S技术应用研究所,福建福州350002;4.福建省三明学院,福建三明365000)
摘要:郁闭度具有获取便捷的特点,是森林资源调查的基本因子之一,也是检测森林状态、检验营林效果的重要指标,并已成为许多重要特征遥感反演的基础数据。另一方面,纹理特征成为遥感信息挖掘的重要方向,并被用于判别单纯依靠光谱特征无法有效识别的信息,但纹理的应用范围与可行性仍缺乏验证。以福建省三明市、将乐县、沙县、延平区4县(市、区)HJ-1 CCD多光谱数据及实测松林郁闭度为主要数据,基于灰度共生矩阵法提取均值、方差、协同性、对比度、相异性、熵、角二阶矩及相关性等8类纹理特征(共计32个),利用单因素方差分析法筛选24个对松林郁闭度变化有所响应的纹理,并分别以单个、单类纹理特征及多纹理特征联合为自变量,建立极弱度郁闭林、弱度郁闭林与中度郁闭林的Fisher判别函数。结果表明,单个纹理特征对松林郁闭度的判别能力普遍较差,仅COR2、COR4、CON1、CON2判别精度高于50%;单类纹理特征对郁闭度的判别能力有所提高,均值、方差、对比度的判别精度高于50%,而相关性的判别精度可达62.7%;多纹理特征联合对松林郁闭度有更高的判别能力,精度达74.6%。由此证明,纹理具备郁闭度的响应能力,在其他特征的遥感反演过程中可以应用,但需要深入挖掘其相关性与响应机制。
关键词:纹理特征;松林郁闭度;Fisher判别分析;HJ-1 CCD多光谱影像;判别精度
纹理特征表现为图像灰度在空间上的变化和重复、反复出现的局部模式及排列规则,可以反映区域中像素灰度级的空间分布属性。诸多研究已经发现,依靠光谱特征开展森林指标反演或状态监测具有局限性,故纹理这一结构变量越来越得到重视,通过深入挖掘纹理与目标变量的耦合关系,为联合光谱、纹理等信息提升森林资源遥感监测水平奠定基础。例如,纹理已成为郁闭度、蓄积量、林龄等林分指标的估算依据,吴飏等[1]在光谱等传统特征的基础上,结合遥感影像的纹理特征估测郁闭度,结果表明结合纹理特征的方法比传统只基于光谱或地形特征的方法的估测精度有较大提高;刘俊等[2]建立了柞树蓄积量与ALOS影像纹理特征及衍生纹理指数的相关关系,得到蓄积量估测的最优模型;李进等[3]探讨了航片纹理图像与马尾松林测树因子间的关系,发现角二阶矩可用于拟合林龄,方差可用于拟合平均树高,但纹理特征与郁闭度的相关程度不高。此外,纹理在检测森林病虫害与生态健康领域也有重要作用[4-5]。郁闭度是传统森林资源调查的一个重要指标,反映林分的疏密状态[6]。因其实地获取的难度较低,且遥感反演的技术也较为成熟,故许多学者通过研究获取难度较大变量(如叶面积指数、生物量等)与郁闭度间的相关关系,来达到该变量反演的目的[7-8],而这些变量对于监测森林资源的存量与健康水平意义重大。虽然已有少数关于郁闭度与遥感影像纹理特征相关性的研究成果,但这种相关性是否密切,结论则不尽相同。为此,本文尝试分析纹理特征对郁闭度的判别能力,检验郁闭度与纹理特征的关系,进一步奠定利用纹理特征开展蓄积量、林龄、叶面积指数等目标变量估测的理论基础。
1研究区概况
选择福建省三明市(26°01′~26°25′N,117°17′~117°48′E)、将乐县(26°26′~27°04′N,117°05′~117°40′E)、沙县(26°06′~26°4l′N,117°32′~118°06′E)、南平市(现南平市延平区26°51′~26°52′ N,117°50′~116°40′ E)等4个县(市、区)作为研究区。4县(市、区)是我国南方重点集体林区,在自然禀赋上相似性较高,据全国第8次森林资源清查结果,各县(市、区)森林覆盖率均在73%以上,将乐县更是超过85%,居全省各县之首。研究区位置示意见图1。
2研究方法
2.1资料收集与处理
(1)郁闭度的获取与分组。2012年2~3月于研究区开展松林调查,每县(市、区)选择12个左右的小班,每个小班随机调查4个以上测点。借助两部麦哲伦手持GPS对每个测点进行同时定位,当定位结果基本一致时记录之,以有效降低定位误差;采用传统的抬头望目测法估算每个测点的林冠郁闭度。随机选择其中128组作为本研究的基础数据。在地形上,采样点分布于各坡向、坡位,坡度介于10~35°;从林龄上看,采样小班涵盖了幼龄、中龄、近熟、成熟、过熟5个龄组。考虑到郁闭度测定有一定的主观性,故对其进行分组。通常认为,当郁闭度<0.2时为疏林,介于0.3~0.4时为极弱度郁闭林,介于0.5~0.6时为弱度郁闭林,介于0.7~0.8时为中度郁闭林,而介于0.9~1.0时为高度郁闭林。测点中不包含疏林及高度郁闭林,极弱度郁闭林、弱度郁闭林、中度郁闭林的测点数量分别为11、84、23个,可以反映研究区松林的实际状况。
(2)遥感影像的获取与预处理。经中国资源卫星应用中心网站(http://www.cresda.com)获取1景与调查时间准同步的HJ-1 CCD多光谱影像,过境时间为:2012年3月26日,轨道号为:451/84。该影像为2级产品,已由地面站作了粗校正。以1∶10 000地形图为参考,基于多项式模型实现该影像的快速几何精校正,像元误差量控制在0.5个像元以内,采用立方卷积法予以重采样。利用三明市、将乐县、沙县、延平区4县(市、区)行政边界图裁剪出研究区影像(图2)。

图1 研究区位置示意图Fig.1 Location diagram of study areas

图2 研究区HJ-1 CCD多光谱遥感影像Fig.2 HJ-1 CCD multi-spectral image of study areas
2.2纹理特征提取
统计分析法、结构分析法和频谱分析法是纹理分析的3种基本方法,其中统计分析法中的灰度共生矩阵法应用最为广泛,本文亦采用该方法提取松林纹理。灰度共生矩阵(GLCM,Gray Level Co-occurrence Matrices)是纹理分析的一种常用方法,该方法提供了像元与像元、像元与整体影像间的空间关系,先依据影像的灰度级数和灰度变化情况计算出4个方向任意2个灰度级相邻出现的概率矩阵,再将该矩阵对称化和归一化处理,得到灰度联合矩阵[9-10]。利用该法可从多个从侧面描述影像纹理特征的8个纹理量。各纹理量计算如下:
(a)均值(Mean):反映纹理图像亮度。公式如下:

(1)
(b)方差(Variance):反映纹理图像灰度的离散情况。公式如下:
(2)
(c)协同性(Homogeneity):表征图像纹理的同质性,值大说明图像不同区域纹理间缺少变化,局部非常均匀,反之亦然。公式如下:
(3)
(d)对比度(Contrast):反映图像清晰度和纹理沟纹深浅程度。对比度值大,则纹理沟纹深,视觉效果清晰;反之,则沟纹浅,效果模糊。公式如下:
(4)
(e)相异性(Dissimilarity):反映纹理的行列差异。公式如下:
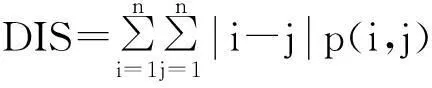
(5)
(f)熵(Entropy):可以度量图像所具有的信息量丰富程度,图像没有纹理,熵值接近为零;图像纹理信息越丰富,图像熵值越大。公式如下:

(6)
(g)角二阶矩(Second Moment):也称能量,度量图像灰度分布均匀性,图像纹理粗,角二阶矩值大,反之值小。公式如下:
(7)
(h)相关性(Correlation):可以衡量灰度共生矩阵的元素在列方向或行方向上的相似程度。公式如下:
(8)
上述各式中,P(i,j)表示灰度联合矩阵中i行j列的元素,μ表示P(i,j)的均值,n为像素值的最大值。
ENVI提供了基于灰度共生矩阵提取纹理特征量的模块,该模块的执行还需要对步长与窗口大小两个参数进行设置。一般地,步长设为(1,1),而窗口大小则包括3×3、5×5、7×7、9×9、11×11等多个尺度。本文仅选择应用较多的5×5窗口[11-12],提取均值、方差、协同性、对比度、相异性、熵、角二阶矩及相关性等8个纹理量(图3)。
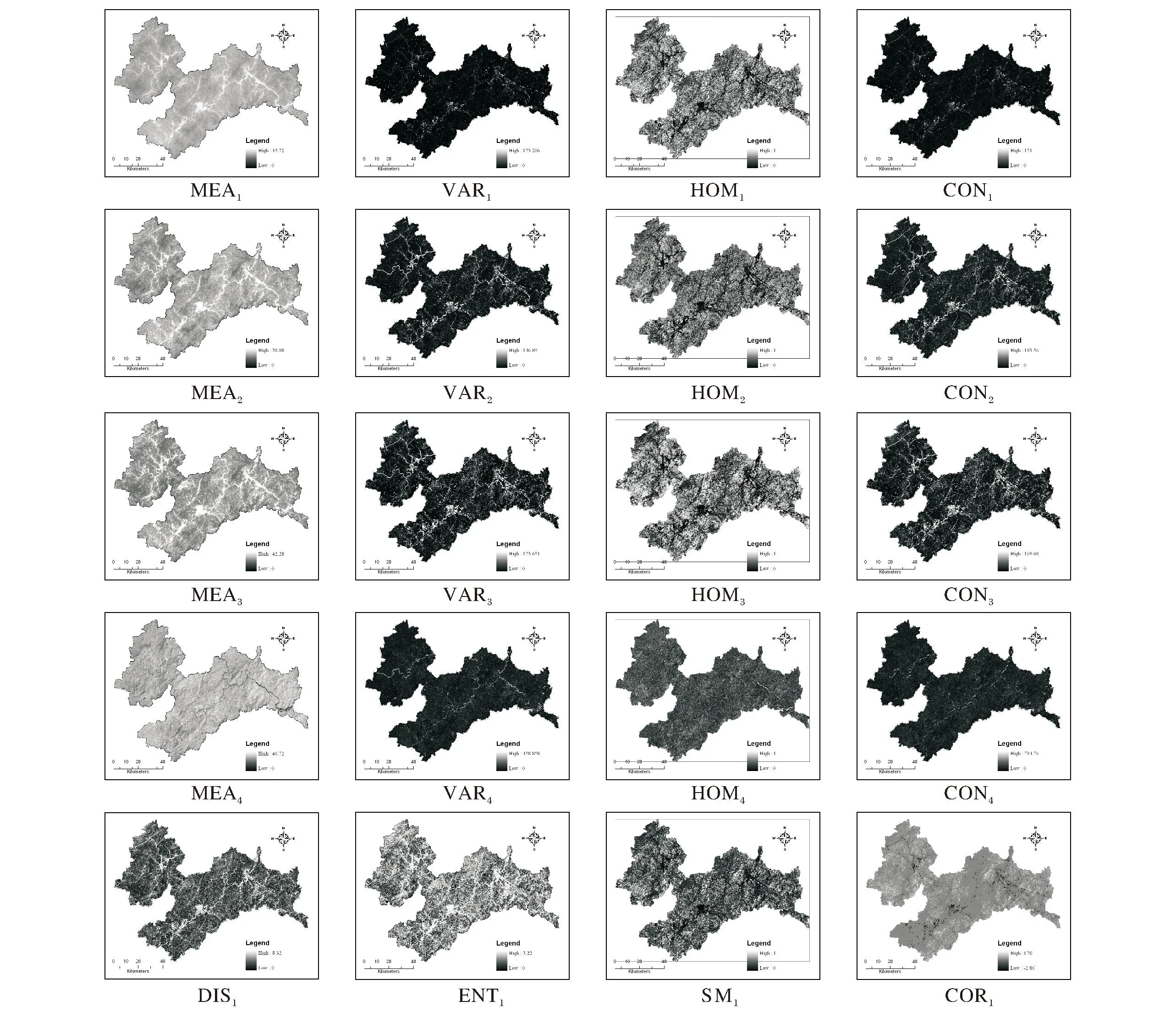
图3 纹理特征图Fig.3 Textual features
2.3单因素方差分析
单因素方差分析(One-way ANOVA)用于解决一个因素下多个不同水平之间的关系问题,其基本应用条件包括独立性、正态性与方差齐性。利用箱图法对样本的正态性进行检验,剔除异常值,保留118个样本;采用Levene法检验方差齐性,当方差不齐时利用Welch法予以校正。在此基础上,若P<0.05,表示有显著差异;若P<0.01,表示有极显著差异;若P>0.05,表示无显著差异。
2.4Fisher判别分析
根据松林纹理特征与郁闭度的单因素方差分析结果,可知哪些纹理特征在不同的郁闭度下具有显著或极显著的差异性,亦即哪些纹理特征对郁闭度的变化有所响应,由此初步筛选了可能对郁闭度具有较强判别能力的纹理特征。在此基础上,需要进一步分析这些纹理特征对松林郁闭度的判别能力,本文采用判别分析法处理之。当收集到一个新的样本数据,要确定该样本数据应当归于已知类别中的哪一类时,该问题即属于判别分析的范畴。判别分析(Discriminant analysis),又称为分辨法,是在分类确定的条件下,依据研究对象的各种特征值判别其类型归属的一种多变量统计分析方法[13-14]。其基本原理是:按照一定的判别准则,建立一个或者多个判别函数,以研究对象的大量样本资料为基础,确定判别函数中的待定系数,并计算判别指标;依此确定新样本数据的归属[15-16]。Fisher判别分析法(Fisher discriminant analysis,FDA)由Fisher于1936年提出,是最为基本的一类判别分析方法,亦称为线性判别分析法,其基本思想是将k组m维样本数据投影到某一个方向,使投影后各组之间尽可能地分开,依据组内方差尽量小、组间方差尽量大的一元方差分析原则确定判别函数,基于一定的判别准则,确定新样本的归属[17,21]。分单个纹理特征、同类纹理特征及多纹理特征联合等3个角度,通过计算Fisher判别精度、绘制判别分类图,以综合比较纹理特征对松林郁闭度的判别能力。为便于比较,同时考虑到实际应用的要求,重点考量各个判别函数的判别精度。若判别精度≤50%,则认为精度差,表明该纹理特征对松林郁闭度的判别能力弱;若判别精度介于50%~60%,则认为精度合格,表明该纹理特征对松林郁闭度有一定的判别能力;当判别精度介于60%~70%,则认为精度中等,表明该纹理特征对松林的判别能力尚可;若判别精度介于70%~80%,则认为精度良好,表明该纹理特征具有较强的判别能力;而当判别精度≥80%,则认为精度优秀,该纹理特征对松林郁闭度的判别能力很强。
3结果与分析
3.1松林纹理特征单因素方差分析
在SPSS 13.0上分别将极弱度郁闭林、弱度郁闭林、中度郁闭林归类为组1、2、3,基于118个样本得到纹理特征的单因素方差分析结果(表1)。表1显示,对于HJ-1 CCD多光谱影像的第1波段,不同郁闭度松林的对比度、相关性两个纹理特征有极显著差异,均值、方差、协同性及相异性等4个纹理特征有显著差异,而熵、角二阶距两个纹理特征的差异不显著;不同郁闭度松林在第2波段的所有纹理特征中均有显著差异,其中方差、对比度、相异性、熵与相关性5个纹理特征的差异达到极显著水平;不同郁闭度松林的均值纹理有显著差异,方差、协同性、对比度、相异性、相关性5个纹理有极显著差异;对于第4波段而言,不同郁闭度松林的熵纹理有显著差异,而方差、对比度与相关性纹理的差异达到极显著水平。对比各纹理的P值,可知相关性纹理的差异性最大,其次为对比度与方差。
表1松林纹理特征单因素方差分析结果
Tab.1ANOVA results of pine forests textual features

3.2纹理特征对松林郁闭度的判别能力分析
3.2.1单个纹理特征对松林郁闭度的判别能力分析分别以多光谱遥感影像各波段生成的8个纹理特征量为自变量,建立极弱度郁闭度、弱度郁闭林、中度郁闭林的Fisher判别函数(表2)。判别函数用于郁闭度的分类,将自变量代入3个判别函数中,可分别求出3个判别函数的值,哪一个判别函数值最大,即表示该样本属于哪一类。表2列出了分别以MEA1等32个纹理特征为自变量的松林郁闭度判别函数,但很显然,以单个纹理为自变量的判别函数对松林郁闭度的判别精度普遍较差,仅有CON1、CON2、COR2、COR4等4个纹理对松林郁闭度有一定的判别能力,以此为自变量的判别函数对郁闭度的判别精度分别为50.8%、52.5%、55.9%、55.9%。具有一定判别能力的纹理特征集中于对比度与相关性,HJ-1 CCD影像的2、4两波段的相关性纹理及1、2波段的对比度纹理对松林郁闭度的状态及其变化具备一定的响应能力。

表2 以单个纹理为自变量的Fisher判别函数及其判别精度

续表2 以单个纹理为自变量的Fisher判别函数及其判别精度
3.2.2同类纹理特征对松林郁闭度的判别能力分析HJ-1 CCD影像有4个波段,分别对应蓝光、绿光、红光与近红外波长,进一步研究不同波段生成的同类纹理特征对松林郁闭度的判别能力有重要意义。以单因素方差分析的结果为依据,将有显著性差异的同类纹理特征作为自变量,建立松林郁闭度的Fisher判别函数(表3)。由于角二阶矩纹理中,仅第2波段的差异达到显著水平,故其所建立的判别函数与3.2.1中一致,不再赘述。表2列示了以同类纹理特征为自变量的松林郁闭度判别函数,并统计了各函数的判别精度。以协同性、相异性、熵等纹理为自变量的函数的判别精度仍不足50%,表明上述类别的纹理特征对松林郁闭度的判别能力弱;均值、方差、对比度3类纹理特征对松林郁闭度具有一定的判别能力,判别精度分别为55.1%、55.1%、51.7%;而以相关性纹理特征为自变量的函数的判别精度达62.7%,达到中等水平,表明其对松林郁闭度的判别能力尚可,可以在郁闭度遥感估算中加以应用。进一步基于典型判别函数制作判别分类图,并将其划分为4个象限(图4)。通过判别分类图可看出118个样本落入不同的象限,而极弱度郁闭林、弱度郁闭林与中度郁闭林则分别形成组中心,离哪个中心越近,则被判定为该类型。对比各图亦可发现,均值、方差、对比度与相关性判别分类图中判定类别与原类别一致的样本数量更多,而其他纹理特征的分类图中的样本分布更为分散。
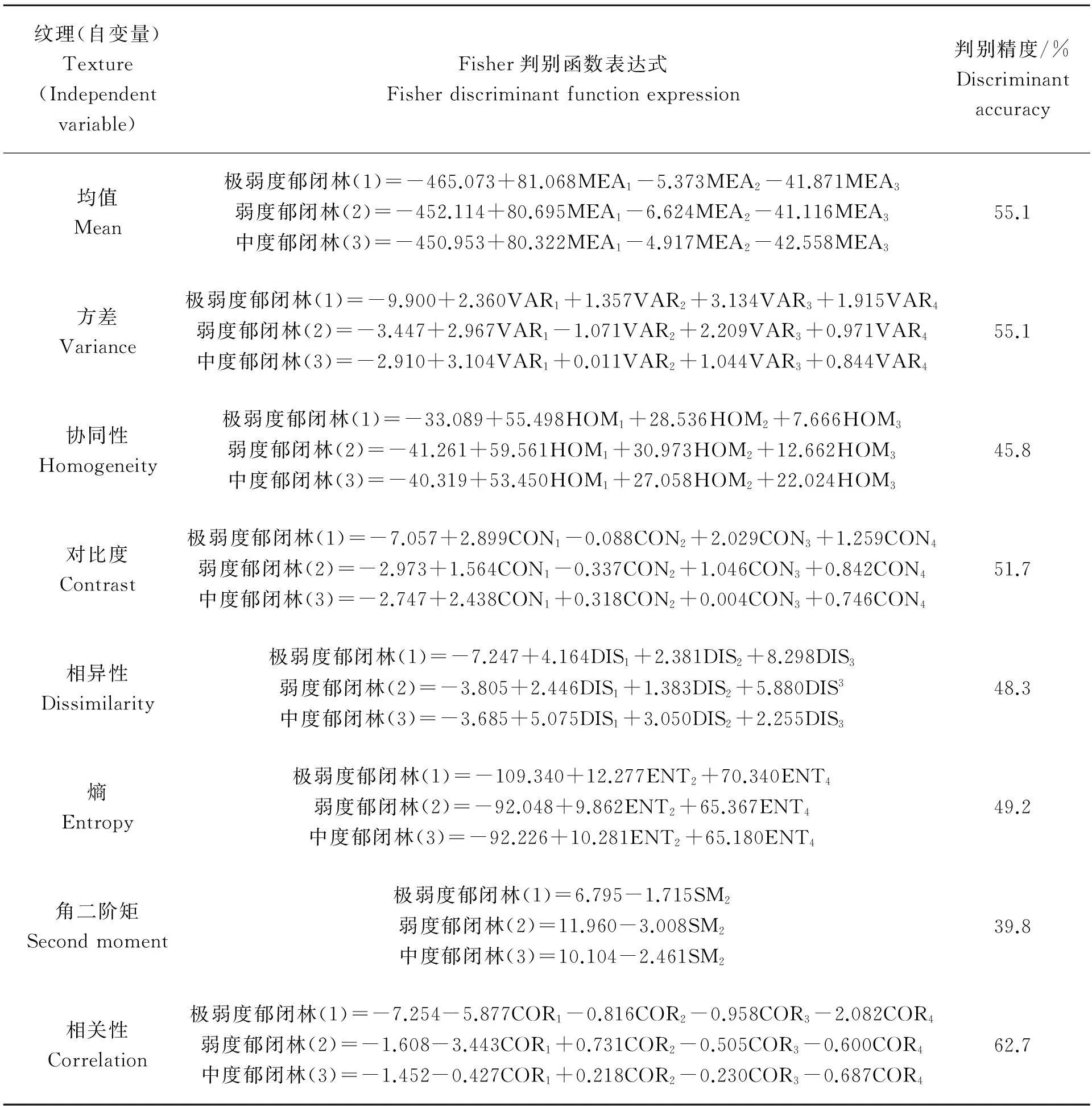
表3 以单类纹理为自变量的Fisher判别函数及其判别精度
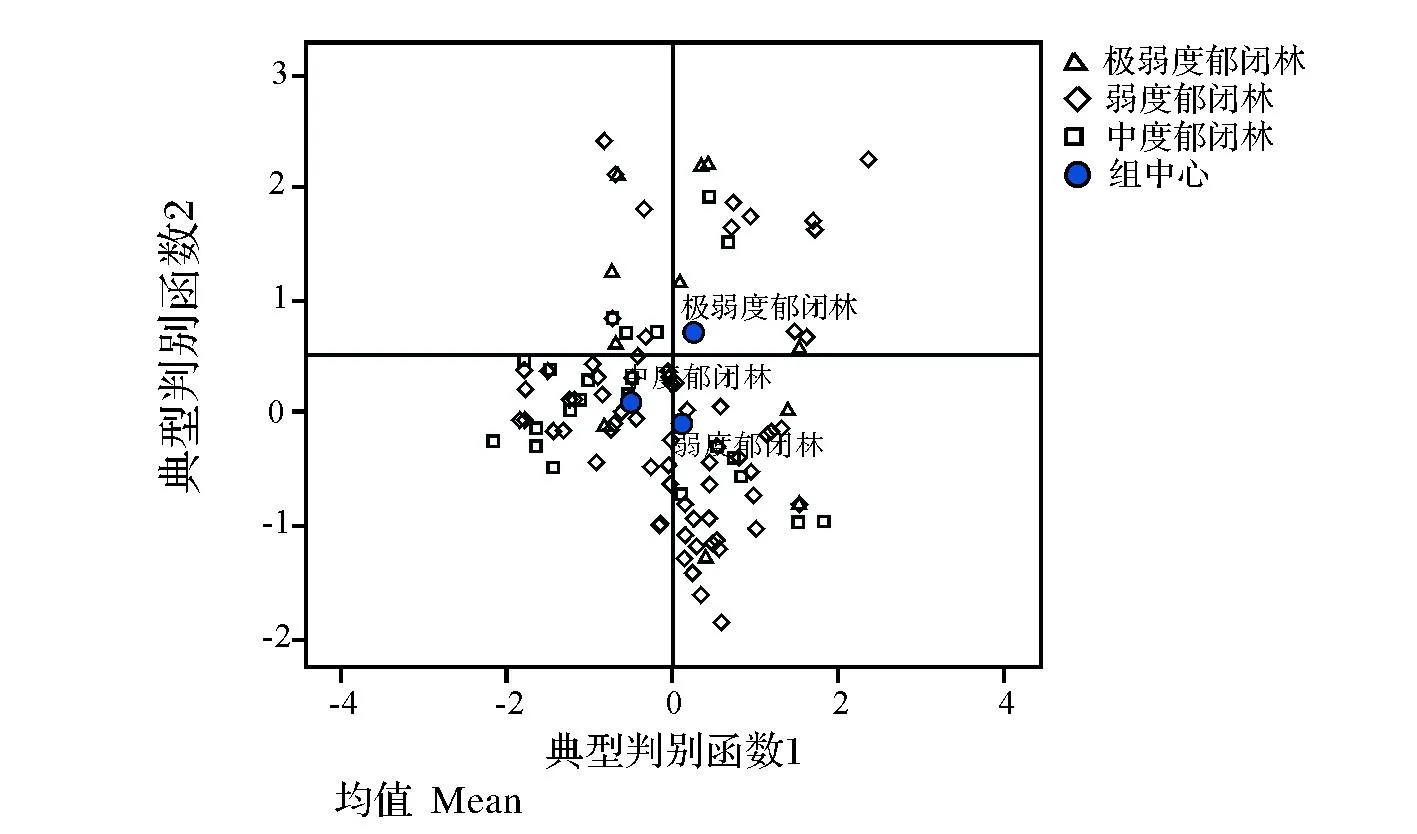

图4 基于单类纹理的典型判别函数的判别分类图Fig.4 Discriminant classification figures based on typical discriminant functions with single class textures

图5 基于多纹理特征的典型判别函数的判别分类图Fig.5 Discriminant classification figures based on typicaldiscriminant functions with multiple textures
3.2.3多纹理特征联合对松林郁闭度的判别能力分析显然,较之于单个波段的纹理特征,单类纹理特征对松林郁闭度的判别能力普遍有较大的提升,并找到已基本上可用于实际应用的纹理量——相关性纹理。在遥感信息分析领域,往往会通过多源信息、多种指标的组合实现目标信息的提取或反演。例如,Ouma et al[22]利用均值、方差等8个纹理特征组合对土地利用类型进行分类,证明纹理可识别光谱无法有效识别的信息,为遥感分类提供重要的数据支持;张锦水等[23]复合光谱、纹理和结构信息等多源数据,对IKONOS高空间分辨率图像进行分类;彭光雄等[24]则选取了CBERS02星CCD5全色波段图像灰度共生矩阵的角二阶矩、对比度、熵和相关性等4个统计量,将其与CCD1-4波段的多光谱图像联合,得到光谱、纹理特征结合的分类精度远高于单纯光谱分类精度的结论;刘健等[11]通过构建最佳纹理量组合实现了竹南方地区竹资源专题信息的有效提取。为此,本文进一步考量多纹理特征联合对松林郁闭度的判别能力。将不同松林郁闭度下差异显著或极显著的24个纹理量作为自变量,利用逐步回归法建立Fisher判别函数(式9~11),并基于典型判别函数绘制判别分类图(图5)。所建立的Fisher判别函数剔除了DIS1、DIS2、DIS3等3个纹理,即1、2、3波段的相异性纹理,保留其余21个纹理作为函数自变量。118个样本中,88个样本判别正确,30个样本判别错误,判别精度达74.6%,远高于单个及同类纹理特征对松林郁闭度的判别精度。按前文对判别精度的分级,该精度已达良好水平,表明多纹理特征联合对松林郁闭度具有较强的判别能力,已经能够满足实际应用要求。由图5可见,极弱度郁闭度的组中心位于2、3象限,而该郁闭度样本亦基本分布于这一区域;弱度郁闭林的组中心位于第1象限,该等级样本也更多地分布于该象限;中度郁闭林的组中心则位于第4象限,该郁闭度等级的样本亦更多地接近于该组中心。
极弱度郁闭林(i)=-2 254.449+54.413MEA1+27.751VAR1+748.165HOM1+214.815CON1-76.556COR1+10.262MEA2-25.179VAR2+1 321.744HOM2+39.876CON2+545.301ENT2+628.571SM2+91.463COR2-30.935MEA3-17.599VAR3+444.574HOM3+76.593CON3+4.745COR3-8.830VAR4+11.756CON4+253.990ENT4+25.322COR4
(9)
弱度郁闭林(j)=-2 261.165+53.278MEA1+30.342VAR1+759.861HOM1+216.132CON1-66.537COR1+11.325MEA2-25.194VAR2+1 301.607HOM2+39.398CON2+558.530ENT2+665.576SM2+95.752COR2-31.355MEA3-16.863VAR3+431.499HOM3+73.597CON3+5.487COR3-10.297VAR4+12.925CON4+258.379ENT4+26.834COR4
(10)
中度郁闭林(k)=-2 262.182+53.927MEA1+28.109VAR1+742.388HOM1+214.574CON1-61.893COR1+11.872MEA2-24.843VAR2+1 313.510HOM2+39.793CON2+558.722ENT2+657.567SM2+94.286COR2-32.448MEA3-17.928VAR3+433.021HOM3+73.699CON3+5.957COR3-10.369VAR4+12.594CON4+259.676ENT4+26.879COR4
(11)
4结论
(1)单个纹理特征判别能力分析表明,仅有以2、4波段的相关性纹理及1、2波段的对比度纹理为自变量的函数的判别精度高于50%,这些纹理对松林郁闭度有一定的判别能力,而其他纹理特征的判别能力均弱,单个纹理特征对松林郁闭度的判别能力普遍较差。
(2)若以同类纹理特征为自变量,所建立的Fisher判别函数的判别精度普遍得到提高,自变量为均值、方差、对比度纹理特征的函数的判别精度均高于50%,对松林郁闭度具有一定判别能力;而以相关性纹理特征为自变量的函数的判别精度为62.7%,达到中等水平,该类纹理特征对郁闭度的判别能尚可。
(3)联合单因素方差分析所筛选的24个纹理特征量,建立的Fisher判别函数的判别精度达74.6%,判别能力远优于单个及同类纹理特征。
(4)总体而言,多纹理特征联合对松林郁闭度的判别能力优于同类纹理特征,而同类纹理特征的判别能力则普遍优于单个纹理特征。由此表明,郁闭度与纹理特征间存在密切联系,纹理特征具备对郁闭度的响应能力,但需要深入挖掘这种相关性与响应机制,由此可助于林分因子的遥感估算及森林状态的动态监测。
参考文献:
[1]吴飏,张登荣,张汉奎,等.结合图像纹理特征的森林郁闭度遥感估测[J].林业科学,2012,48(2):48-53.
[2]刘俊,毕华安,朱沛林,等.基于ALOS遥感数据纹理及纹理指数的柞树蓄积量估测[J].农业机械学报,2014,45(7):245-254.
[3]李进,王鑫,张园.灰度共生矩阵纹理特征与马尾松林测树因子关系初探[J].浙江林业科技,2010,30(3):68-71.
[4]Moskal L M,Franklin S E.Relationship between airborne multispectral image texture and aspen defoliation[J].International Journal of Remote Sensing,2004,25(14):2701-2711.
[5]Kayitakire F,Hamel C,Defouray P.Retrieving forest structure variables based on image texture analysis and IKONOS-2 imagery[J].Remote Sensing of Environment,2006,102(3-4):390-400.
[6]许章华,龚从宏,刘健,等.利用郁闭度与HJ-1多光谱数据估算马尾松林叶面积指数[J].植物资源与环境学报,2013,22(1):29-35.
[7]Ex S A,Smith F W.Stand density index estimates leaf area index in uneven-aged ponderosa pine stands[J].Western Journal of Applied Forestry,2013,28(1):9-12.
[8]李明泽,毛学刚.基于郁闭度联立方程组模型的森林生物量遥感估测[J].林业科学,2014,50(2):85-91.
[9]杨志刚.纹理信息在遥感影像分类中的应用[D].南京:南京林业大学,2006.
[10]Kulkarni S B,Kulkarni R B,Kulkarni U P,et al.GLCM-Based multiclass iris recognition using FKNN and KNN[J].International Journal of Image and Graphics,2014,14(3):1450010.
[11]刘健,余坤勇,许章华,等.竹资源专题信息提取纹理特征量构建研究[J].遥感信息,2010(6):87-94.
[12]何春阳,曹鑫,史培军,等.基于Landsat7 ETM+全色数据纹理和结构信息复合的城市建筑信息提取[J].武汉大学学报:信息科学版,2004,29(9):800-804.
[13]Alonzo M,Roth K,Roberts D.Identifying Santa Barbara's urban tree species from AVIRIS imagery using Canonical Discriminant Analysis[J].Remote Sensing Letters,2013,4(5):513-521.
[14]Liao W Z,Pizurica A,Scheunders P,et al.Semisupervised local discriminant analysis for feature extraction in hyperspectral images[J].IEEE Transactions on Geoscience and Remote Sensing,203,51(1):184-198.
[15]Wang Y W,Dunn B L,Arnall D B.Assessing nitrogen status in potted geranium through discriminant analysis of ground-based spectral reflectance data[J].Hortscience,2012,47(3):343-348
[16]Prades C,Gomez-Sanchez I,Garcia-Olmo J,et al.Discriminant analysis of geographical origin of cork planks and stoppers by near infrared spectroscopy[J].Journal of Wood Chemistry and Technology,2012,32(1):54-70.
[17]Chen X H,Wang S Q,Chen J,et al.New algorithm for spectral mixture analysis based on Fisher Discriminant Analysis:evidence from laboratory experiment[J].Journal of Infrared and Millimeter Waves,2009,28(6):476-480
[18]Du Q.Modified Fisher’s Linear Discriminant analysis for hyperspectral imagery[J].IEEE Geoscience and Remote Sensing Letters,2007,4(4):503-507.
[19]李秀珍,王成华,宋刚.基于Fisher判别分析法的潜在滑坡判识模型及其应用[J].中国地质灾害与防治学报,2009,20(4):23-26.
[20]朱永生.实验数据多元统计分析[M].北京:科学出版社,2009.
[21]王文川,吴海波,赵晓慎,等.基于Fisher判别分析法的泥石流预报模型研究[J].水土保持通报,2011,31(6):104-107.
[22]Ouma Y O,Tetuko J,Tateishi R.Analysis of co-occurrence and discrete wavelet transform textures for differentiation of forest and non-forest vegetation in very-high-resolution optical-sensor imagery[J].International Journal of Remote Sensing,2008,29(12):3417-3456.
[23]张锦水,何春阳,潘耀忠,等.基于SVM的多源信息复合的高空间分辨率遥感数据分类研究[J].遥感学报,2006,10(1):49-57.
[24]彭光雄,李京,何宇华,等.利用纹理分析方法提取CBERS02星CCD图像土地覆盖信息[J].遥感技术与应用,2007,22(1):8-13.
Discriminant Abilities of Textual Features on
Pine Forest Canopy Density
XU Zhang-hua1,LIU Jian3,4,YU Kun-yong3
(1.College of Environment and Resources,Fuzhou University,Fuzhou 350116,China;2.Fujian Provincial Key Laboratory of Remote Sensing of Soil Erosion and Disaster Protection,Fuzhou 350116,China;3.Institute of Geomatics Application,Fujian Agriculture and Forestry University,Fuzhou 350002,China;4.Sanming University,Sanming 365000,China)
Abstract:Canopy density,which can be easily obtained,is one of the basic factors in forest resources survey,and also an important factor in forest state detection and forest management effect test,and has become a basic datum in remote sensing retrieval of many features.On the other hand,texture has become the significant direction of remote sensing data probing,but the application scope and feasibility of texture are still to be verified.Taking HJ-1 CCD multi-spectral image and measured pine forest canopy density materials in four counties (cities,districts) of Sanming,Jiangle,Shaxian and Yanping of Fujian Province as the main data,eight classes of textual features (total 32) such as mean,variance,homogeneity,contrast,dissimilarity,entropy,second moment,
correlation were extracted with GLCM,24 textures affecting changes in canopy density were screened with ANOVA,and Fisher discriminant functions of very-weak canopy forest,weak canopy forest and moderate canopy forest independent variables respectively as single texture,single class textures,combination of multiple textures were constructed.The results showed that the discriminant abilities of single textual features on pine forests canopy density were generally poor,only the accuracies of COR2,COR4,CON1,CON2were above 50%;the discriminant accuracies of single class textures increased,the accuracies of mean,variance,contrast were above 50%,the correlation reached 62.7%;the combination of multiple textures had higher discriminant ability on pine forests canopy density with an accuracy up to 74.6%.Therefore,texture has response ability to canopy density,and can be used in remote sensing retrieval of other features,but the relationships and response mechanisms should be deeply probed.
Key words:textual features;pine forest canopy density;Fisher Discriminant Analysis;HJ-1 CCD multi-spectral image;discriminant accuracy
作者简介:许章华(1985—) ,男,博士,讲师,主要从事资源环境遥感、城乡规划与GIS应用,E-mail:fafuxzh@163.com。
基金项目:国家自然科学基金项目(30871965)、福建省科技计划重点项目(2011N0031)和福州大学人才基金项目(XRC-1345)
收稿日期:2015-04-22修回日期:2015-06-17
中图分类号:S771.8;TP753
文献标志码:A
文章编号:1000-2286(2015)06-1016-11
许章华,刘健,余坤勇.纹理特征对松林郁闭度的判别能力研究[J].江西农业大学学报,2015,37(6):1016-1026.

