面齿轮轮齿刚度计算方法研究

黄鹏，李政民卿

(南京航空航天大学 江苏省精密与微细制造技术重点实验室, 江苏 南京 210016)



面齿轮轮齿刚度计算方法研究

黄鹏，李政民卿

(南京航空航天大学 江苏省精密与微细制造技术重点实验室, 江苏 南京 210016)

摘要：基于Buckingham的观点，将面齿轮齿形看作是由沿齿长方向一系列变压力角的齿条组成，得到沿轴向和径向都为变截面的面齿轮简化齿形，获得了面齿轮轮齿啮合变形的计算公式，求解出了面齿轮的轮齿刚度。与有元法的分析结果进行比较，二者相对误差较小，验证了面齿轮轮齿刚度计算方法的可行性。

关键词：面齿轮；轮齿变形；轮齿刚度；计算方法

面齿轮传动是圆柱齿轮与面齿轮相啮合的齿轮传动，具有重合度大、无需防错位设计、与面齿轮啮合的直齿圆柱齿轮无轴向力作用和传递动力性能优越等优点[1,3]；据波音公司报道[4]，采用面齿轮传动作为主减速器的阿帕奇Brock-Ⅲ型直升机已于2009年11月23日首飞成功。

在面齿轮传动中，由面轮齿轮齿啮合变形引起的刚度激励是其传动中的主要动态激励之一，面齿轮传动过程中的综合啮合刚度是研究动力学的基础，而确定面齿轮轮齿刚度是研究面齿轮传动综合啮合刚度的一项重要工作，因此有必要对面齿轮轮齿刚度的计算方法开展研究。

圆柱齿轮和圆锥齿轮啮合刚度的计算和测量方法从20世纪就开始研究[5,6]，并取得了一定的研究成果。Isa Yesilyurt等人[7]对圆柱齿轮的单齿啮合刚度的理论计算方法进行了研究，并采用模态法来测量圆柱齿轮的单齿刚度。而目前对于面齿轮轮齿刚度多采用有限元法计算得到，其计算效率低。本文对面齿轮轮齿刚度的解析计算方法进行研究，寻求一种高效准确的面齿轮轮齿刚度计算方法。

1 面齿轮齿形分析

基于Buckingham的观点[8]：面齿轮齿形可以看作是沿齿长方向一系列变压力角的齿条组成，如图1(a)所示；其沿齿长方向上某一截面的齿形分析，如图1(b)所示。

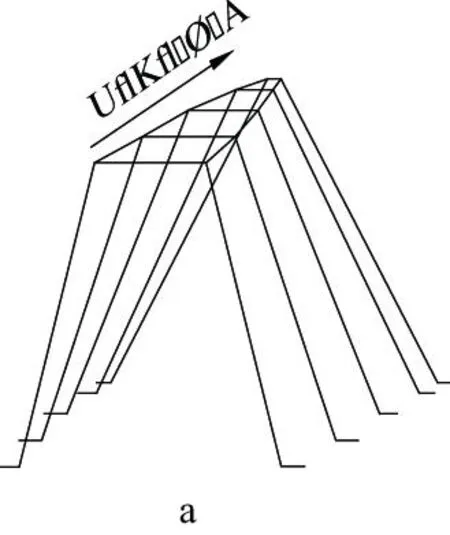
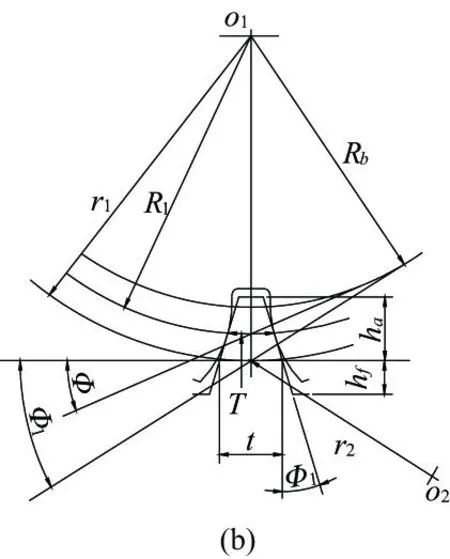
图1　面齿轮齿形及齿形分析图

根据图1(b)中的几何关系，可求出面齿轮啮合半径r2处的齿厚t[8]为：

t=2r1[(T/2R1)+invφ1-invφ]

(1)

式中：r1为渐开线直齿轮啮合半径；T为渐开线直齿轮在分度圆处的齿槽宽，其值为：

T=πm/2

其中：m为模数；R1为渐开线直齿轮分度圆半径；φ为渐开线直齿轮压力角；φ1为节点压力角，其值为：

φ1=arccos(Rb/r1)

其中Rb为渐开线直齿轮基圆半径。

齿条的齿顶高ha为：

ha=r1-Rr-c

(2)

式中：Rr为渐开线直齿轮齿根圆半径；c为齿顶间隙。

齿条的齿根高hf为：

hf=Roc-r1

(3)

式中Roc为渐开线直齿轮齿顶圆半径。

根据上述面齿轮齿形分析方法，以表1所列面齿轮参数在matlab中绘制无过渡圆弧的面齿轮单齿模型，如图2所示。

表1　面齿轮传动的齿轮副主要几何设计参数

图2　面齿轮单齿模型仿真图

2面齿轮轮齿刚度计算方法

基于面齿轮的复杂齿形，在求解面齿轮轮齿刚度时需要对面齿轮齿形进行合理简化。根据仿真图2，可将面齿轮齿形简化成由一系列沿齿高方向变化的梯形截面组成，如图3所示。

图3　面齿轮单齿模型简化示意图

根据图3中面齿轮齿形的简化形式，其轮齿刚度的解析法求解思想仍然基于圆柱齿轮轮齿刚度的当量齿轮解析分析方法，即面齿轮的轮齿综合弹性变形包括轮齿的弯曲变形、剪切变形、接触变形以及由齿根基础弹性倾斜引起的附加变形[9-11]。分析中，先通过求解轮齿各单一变形后，再将其相加，得出面齿轮轮齿在单位载荷作用下接触点处的总变形量δf为：

δf=δ1+δ2+δ3+δ4

(4)

式中：δ1为弯曲变形；δ2为剪切变形；δ3为轮齿接触变形；δ4为齿根基础弹性倾斜引起的附加变形。

根据刚度和变形量-柔度的关系可知，面齿轮在接触点处的轮齿刚度kf为:

kf=1/δf

(5)

2.1　面齿轮轮齿的弯曲变形和剪切变形

面齿轮轮齿的弯曲变形和剪切变形分析中，将在接触范围内的轮齿分成若干小段i，并把小段i看成一个悬臂梁，如图4(a)所示；每个小段i沿齿长方向的截面可看作是随面齿轮齿高方向变化的梯形截面，如图4(b)所示。

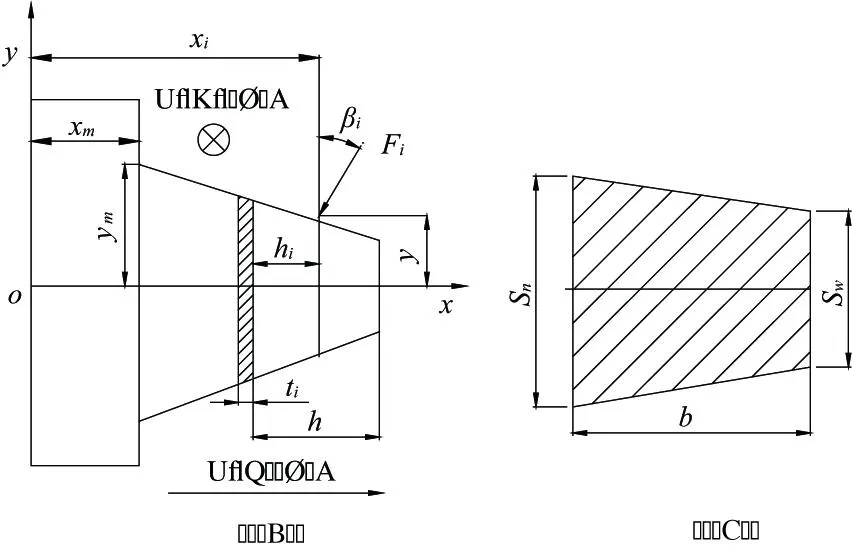
图4　面齿轮轮齿简化成的悬臂梁模型

根据截面上切应力的分布规律作以下2个假设[12]：

1) 横截面上各点切应力的方向都平行于剪应力的方向；

2) 切应力沿截面宽度均匀分布。

根据上述假设，面齿轮轮齿在接触点处的弯曲变形和剪切变形可通过对各小段的变形量求和获得。

面齿轮轮齿在接触点处弯曲变形包括单位长度载荷作用在小段i上产生的弯矩变形和横向变形。

根据图4(a)所示，取小段i的厚度为ti，截面面积为Ai，截面模量为Ii；小段i至载荷作用点沿x方向的距离为h，载荷作用点处的半齿厚为yi，齿根处的半齿厚为ym；泊松比为v，弹性模量为E；面齿轮齿宽为b；载荷与y轴间的夹角为βj；则单位长度载荷Fj作用在小段i上的弯矩变形δ11为：

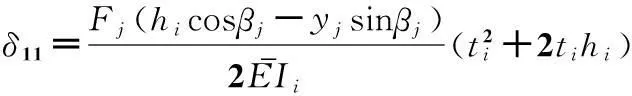
(6)

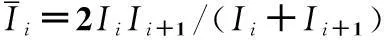
由Fj对小段i产生的横向变形δ12为：

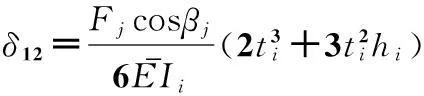
(7)

因此，单位载荷作用下小段i的弯曲变形δbi为：

δbi=δ11+δ12

(8)

由Fj对小段i产生的剪切变形δsi为：

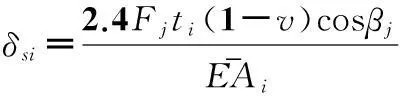
(9)

根据图4(b)可知，由于各小段的截面均是随面齿轮齿高位置变化的梯形截面，因此其截面模量Ii为：

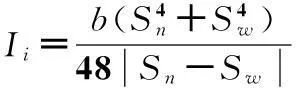
(10)

截面面积Ai为：

Ai=b(Sn+Sw)/2

(11)

式中，沿齿高方向任意高度h处的Sn、Sw可采用图5所示模型计算。

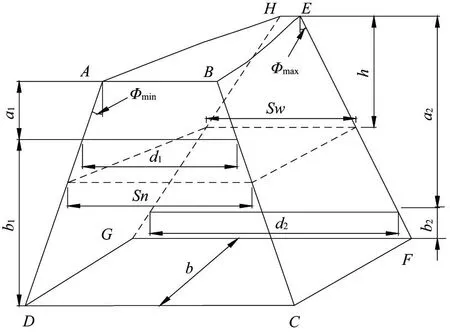
图5　Sn，Sw的计算模型

根据图5可知，利用梯形ABCD可求得:

Sn=d1+2(h-a1)tanφmin

(12)

式中：φmin为面齿轮内半径节线处的压力角；d1为面齿轮内半径节线处的齿厚；a1为面齿轮内半径节线位置到齿顶的距离。d1和a1的计算式分别为：

d1=2r11(T/2R1-invφmin+invφ)

a1=r11-Rr-c

式中r11为面齿轮内半径。

利用梯形EFGH可求得:

Sw=d2+2(h-a2)tanφmax

(13)

式中：φmax为面齿轮外半径节线处的压力角；d2为面齿轮外半径节线处的齿厚；a2为面齿轮外半径节线位置到齿顶的距离。d2和a2的计算式分别为:

d2=2r12(T/2R1-invφmax+invφ)

a2=r12-Rr-c

式中r12为面齿轮外半径。

利用式(8)-式(13)，可分别求出面齿轮轮齿在载荷作用点处沿载荷方向的弯曲变形和剪切变形，其中弯曲变形δ1为:

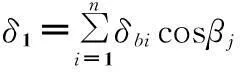
(14)

剪切变形δ2为:

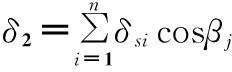
(15)

式中n为小段i的个数。

2.2　面齿轮轮齿接触变形和齿根基础弹性倾斜引起的附加变形

面齿轮接触变形分析是以布希涅斯克问题的解为基础，根据物体表面上有相同距离的点在公切面上形成类椭圆区域的结论，得出面齿轮轮齿的接触变形δ3[13]为：

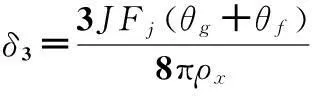
(16)

式中：J为椭圆积分系数，可通过查椭圆积分系数表获得；ρx为接触区域椭圆长半径，θg和θf可由下式确定：

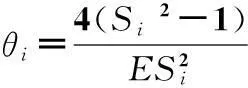
(17)

其中：i分别为g和f；Si为材料纵向延伸和横向压缩比的系数；E为材料的弹性模量。

面齿轮齿根基础弹性倾斜引起的附加变形δ4[14-15]为：

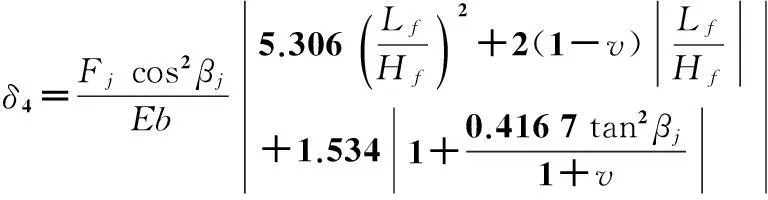
(18)

式中：Lf=xj-xm-yjtanβj，Hf=2ym。

3轮齿刚度解析法的可行性验证

为验证上述面齿轮轮齿刚度计算方法的可行性，将解析法计算结果与有限元法计算结果进行对比分析。根据表1中所列面齿轮参数，建立面齿轮有限元分析模型，如图6所示。

图6　面齿轮有限元分析模型

利用图6中模型，将计算得到的变形量转换为轮齿刚度并与上述面齿轮轮齿刚度解析计算方法进行比较，如表2所示。

表2　解析法与有限元法的刚度计算比较表

采用有限元法和本文介绍的方法计算得到的面齿轮轮齿变形量及轮齿刚度沿齿高方向变化的曲线分别如图7(a)和图7(b)所示。

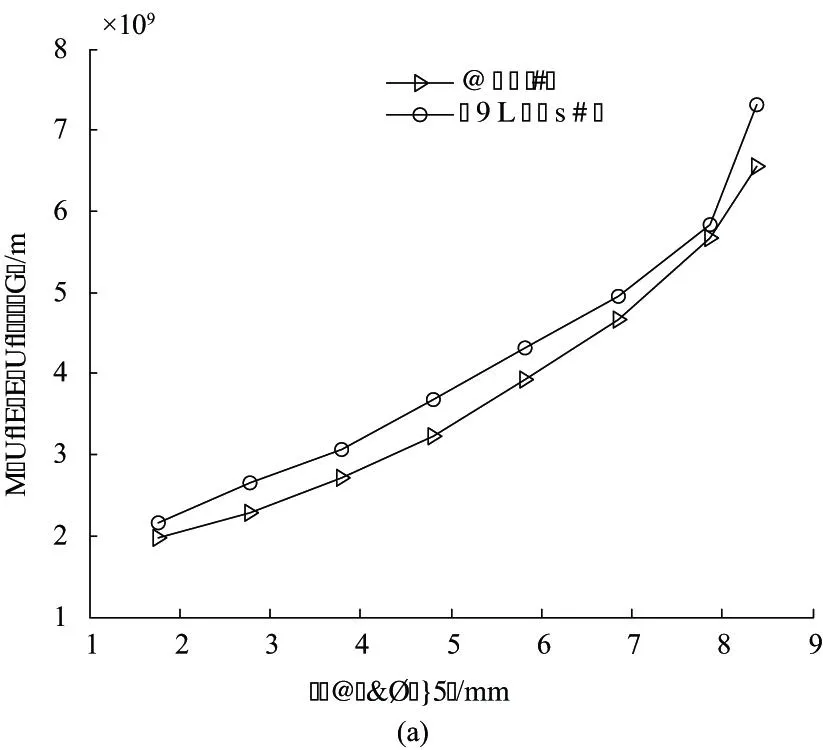
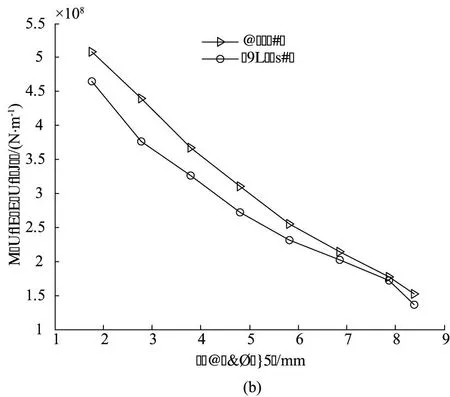
图7　解析法与有限元法计算结果对比

根据图7可知，解析法计算的面齿轮轮齿啮合变形及轮齿刚度与有限元法分析所得结果相差较小。为进一步分析面齿轮刚度解析法的可行性，定义解析法与有限元法的相对平均偏差η为:

(19)

式(19)中，N为接触点个数。利用式(19)对表2中数据分析可知，解析法与有限元法的相对平均偏差为10.32%。因此，上述面齿轮轮齿刚度的解析计算方法是可行的。

4结论

1) 基于Buckingham的观点，将面齿轮齿形看成是由一系列变压力角齿条组成，形成了用于求解面齿轮轮齿刚度的齿形建模方法。

2) 将无过渡圆弧的面齿轮齿形看作是沿轴向和径向均为变截面的梯形弹性悬臂梁，运用材料力学方法，形成了面齿轮轮齿刚度的解析计算方法。

3) 分别运用解析法和有限元法计算出了面齿轮轮齿刚度，得到了轮齿刚度沿齿高方向的变化规律，两种计算方法得到的结果相差很小，证明了面齿轮轮齿刚度的计算方法的可行性。

参考文献:

[1] LITVIN F L, WANG J C, BOSSLER R B Application of face gear drives in helicopter transmissions [J]. Journal of Mechanical Design, Transactions of the ASME, 1994, 116 (3) : 672～676.

[2] HANDSCHUH R F, LEWICKI D G, BOSSLER R B. Experimental testing of prototype face gears for helicopter transmissions [J]. Journal of Aerospace Engineering, 1994, 208 (2) : 129～136.

[3] BILL R C. Summary highlights of the advanced rotorcraft transmission (ART) program [R]. American Inst of Aeronautics and Astronautics, New York, 1992.

[4] MESA Ariz. Boeing AH-64D Apache Block III structures test aircraft makes 1st flight [EB/OL]. [2009-12-4]. http://boeing.mediaroom.com/index.php?s=20295&item=977.

[5] MONSAK P, KAZEM K. Efficient evaluation of spur gear tooth mesh load using pseudo-interference stiffness estimation method [J]. Mechanism and Machine Theory. 2002, 37(8): 769~786.

[6] COMELL R W. Compliance and stress sensitivity of spur gear teeth [J]. Journal of Mechanical Design, 1981,103: 447~459.

[7] ISA Y, GU F, ANDREW D B. Gear tooth stiffness reduction measurement using modal analysis and its use in wear fault severity assessment of spur gears [J]. NDT&E International 2003,36 (5) :357~372.

[8] BUCKINGHAM E. Analytical mechanics of gears [M]. New York, Dover Publications, 1949: 302~320.

[9] BAND R V，PETERSON R E. Load and stress cycle in gear teeth [J]．Mechanical Engineering，1929，51(9)：653～662.

[10] WEBER C．The deformation of loaded gears and the effect on their load carrying capacity [J]．Sponsored Research (Germany) ，British Dept．of Scientific and Industrial Research，Report，1949 (3).

[11] ATTIA A Y． Deflection of spur gear teeth cut in thin rims [J]．ASME Eng. Ind，1964，86(4)： 333~341.

[12] 刘鸿文．材料力学[M]. 北京：高等教育出版社，2004.

[13] 李政民卿，朱如鹏．面齿轮传动的承载接触分析[J]．南京航空航天大学学报，2010，42(2)：219~223.

[14] 吴俊飞，郭建章．变厚齿轮轮齿啮合综合刚度确定方法研究[J]．青岛化工学院学报，2002，23(1)：74~76.

[15] 李润方，王建军.齿轮系统动力学-振动、冲击、噪声[M]．北京：科学出版社，1996.

Research on Method of Calculating Stiffness of Face Gear Tooth

HUANG Peng，LI ZHENG min-qing

( Jiangsu Key Laboratory of Precision and Micro-Manufacturing Technology,

Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:Based on Buckingham’s standpoint, along the length of the tooth of face gear , any one of its sections can be considered as a section of rack with varying pressure angle. According to above theory, the tooth form of the face gear is simulated successfully. The calculating method of the tooth’s stiffness of the face gear is obtained. Compared with the result of analyzing the tooth’s stiffness by FEM, both relative errors are almost same. it is proved that the calculation method for its stiffness is correct.

Keywords:face gear; gear tooth deformation; gear tooth stiffness; calculating method

中图分类号：TH132.429

文献标志码：A

文章编号：1671-5276(2015)02-0046-04

作者简介：黄鹏(1987-)，男，湖北随州人，硕士研究生，主要从事机械传动与减振降噪研究。

基金项目：国家自然科学基金(51105194)；国家留学基金资助(201206835011)

收稿日期：2014-11-08