基于灵敏度分析的某密封结构优化设计

陈伟，赵威，王程

(1. 南京理工大学 机械工程学院, 江苏 南京 210094； 2. 中国人民解放军73841部队，江苏 南京 210003； 3. 中国人民解放军75250部队，广东 广州 510800； 4. 中国人民解放军94860部队，江苏 南京 210049)



基于灵敏度分析的某密封结构优化设计

陈伟1,2，赵威1,3，王程4

(1. 南京理工大学 机械工程学院, 江苏 南京 210094； 2. 中国人民解放军73841部队，江苏 南京 210003； 3. 中国人民解放军75250部队，广东 广州 510800； 4. 中国人民解放军94860部队，江苏 南京 210049)

摘要：在某试验装置密封结构的设计中引入灵敏度分析理论，通过对密封元件的相关结构参数相对于密封时间以及最大Mises应力的灵敏度分析，确定各设计参数对密封时间和应力变化的影响程度。并根据灵敏度分析结果，确定最适合的优化方案，从而得到密封结构各元件的最优结构尺寸。该设计思路可以为优化参数的设置提供参考。

关键词：密封结构; 灵敏度分析; 优化设计

0引言

文中研究的密封结构用于过载试验装置工作时内膛火药气体的密封。过载试验装置工作过程与火炮发射过程相同，利用火药燃烧产生的大量高温高压气体推动试验载体加速运动来获得需要的冲击加速度，从而研究不同过载加速度对试验载体内部元器件的影响。因此工作过程中内膛高温高压火药气体的密封至关重要。

1密封结构

由筒体、压盖、导向增压杆和密封环几部分组成。其中增压杆一端与压盖配合，另一端与外界大气连通，利用杆两端的压力差带动压盖挤压筒体，使筒体产生弹性径向膨胀变形，消除筒体与炮身内壁之间的初始装配间隙，最终贴紧炮身内壁后实现火药气体的完全密封。其结构如图1所示。增压杆的数量和直径决定了密封结构承压的工作范围。

如图1所示，影响密封结构密封性能的参数主要有筒体壁厚t1、初始配合间隙t2、筒体锥角α和增压杆直径d。为方便后续的参数化过程，将密封结构的尺寸参数以坐标的形式进行表示，如图2所示。由于传统的结构设计过程中一般根据经验对结构参数进行简单选取，所以导致结构种类很多，研发周期长，这样既不能够设计出最优结构，也不利于产品的应用。

图1　密封结构示意图

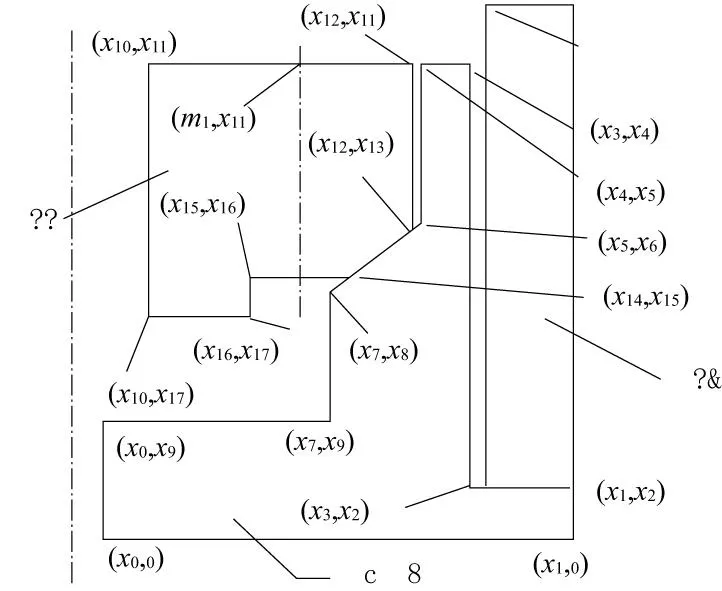
图2　密封结构尺寸的坐标形式

在进行密封结构设计时都希望能够最大限度地提高结构的密封可靠性。密封可靠性是指在满足密封结构各构件强度的前提下，尽可能延长密封时间。面对以上众多的参数，需要通过灵敏度分析来确定对密封结构密封性能影响较大的参数，再对其进行优化，从而提高性能。

2灵敏度分析

2.1　基本理论介绍

结构分析中的灵敏度分析是指密封结构性能参数uj对密封结构设计参数xi变化的敏感性。灵敏度定义为：

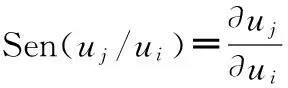
(1)

式中：Sen——灵敏度值；

uj——密封结构性能参数，如强度、密封时间等；

xi—— 密封结构设计参数。

本文利用Isight软件提供的DOE模块进行灵敏度分析。Isight的DOE模块提供了直观方便的灵敏度分析的Pareto图和主效应图，让设计者能够从容的分析参数特征，方便获得设计参数对性能参数的影响大小。

ISIGHT的DOE模块提供Full factorial design，Central composite design，Parameter study，Orthogonal arrays，Latin hypercube design，Optimal Latin hypercube design和Data file 7种方法，通过这些系统、有效的方法来分析设计空间，进行设计变量筛选，估计设计参数影响和辨别关键设计变量间的交叉影响关系。其中拉丁方试验设计方法是一种常用的试验设计方法，也是一种比较有效可靠的试验设计方法。

拉丁方试验设计方法的主要原理：首先建立一个m维单位立方体，记为Cm=[0,1]m，并从中选出n个点；然后再把每一维坐标区间[0,1]分为n等份，并用标号i记小区间[i-1/n,i/n]，用(π1j∧πnj)记第n维坐标的n个标号，(1∧n)的一个随机排列。假设这m个随机排列具有相互独立的特点，则可以得到一个n×d阶的随机矩阵(πij)；然后令:

Cij=(πij-1/2+uij)/n，

i=1,∧,n;j=1,∧,m

(2)

其中:uij是与π独立的[-1/2,1/2]上均匀分布的一个Monte Carlo抽样样本。那么选取的这n个点Ci=(Ci1,∧,Cin),i=1,∧,n就是一个LHS样本。

LHS样本非常具有代表性，也有良好的散布均匀性，又因为它的抽取具有随机性，因此搜索能力更强。在拉丁方实验中是通过较少的试验来获得更多的信息，并且近似值的高精度也因为广泛分布的数据点而得到了保证。本文的灵敏度分析采用拉丁方试验设计方法进行。

2.2　 参数化建模

进行设计参数的灵敏度分析的前提条件是要将结构进行参数化，并建立结构的参数化有限元模型。进行灵敏度分析时， ISIGHT调用密封结构的参数化文件，提交给有限元分析软件进行计算，并从结果文件中提取仿真输出，通过数据分析整理，获得设计参数对性能参数的灵敏度信息。本文采用多学科优化软件ISIGHT集成有限元分析ABAQUS软件来实现，参数化模型文件利用python语言对ABAQUS进行二次开发来获取。

Python是Abaqus软件的标准语言，在cae中所有的操作都可以通过Python脚本命令完成，同时每一步cae操作也都会产生相应的python命令。在进行参数化建模获取python脚本时，先在cae中进行相应的建模操作，然后对生成的abaqus.rpy文件进行修改，对自己要进行参数分析的参数赋值，生成可供Abaqus调用的*.py文件，该文件包含模型建立、参数设置、网格划分、载荷施加、边界条件设定、作业提交、计算结果提取等全流程命令。每改变一次设计参数，有限元模型会自动提交到ABAQUS求解器进行计算，通过结果提取程序分别提取其最大应力(maxMise )、最大径向膨胀变形(maxU1)和最长密封时间(maxsealtime)等目标响应结果，ISIGHT再根据该分析结果对设计参数进行新一轮的调整。应力与位移的结果提取程序如图3和图4所示。

图3　应力提取程序

图4　位移提取程序

为了充分了解设计参数对性能参数的影响程度，初始设计变量围绕主要影响因素选取。密封性能主要受筒体和压盖的结构影响，故将筒体和压盖的结构尺寸设计成可变参数，同时导向增压杆的直径Dz和位置m1也是密封性能好坏的关键因素，需要设计成可变参数。

目标函数初定为密封结构的径向位移最大和密封时间最长，等效于贴合最紧密和接触时间最长。约束条件为密封元件Maxmises不超过密封元件的材料强度极限1350MPa，同时对于锥角的要求是不小于摩擦角，即8°30′<α<75°。

2.3　灵敏度分析结果

在ISIGHT软件的分析结果中，通过Pareto图可以清晰明了的查看单个分析变量和分析变量之间相互作用对目标函数的影响程度。Pareto图按照对响应参数影响程度的大小(以占总影响的百分数比值表示贡献率大小，所有因子的影响程度和为100%)，按照高到低的顺序排列出所有分析变量及分析变量间的相互作用。图5为采用拉丁方试验方法时单个分析变量及其组合对密封结构Mises应力影响的Pareto图，图6为单个分析变量及其组合对密封结构径向位移的主效应图。

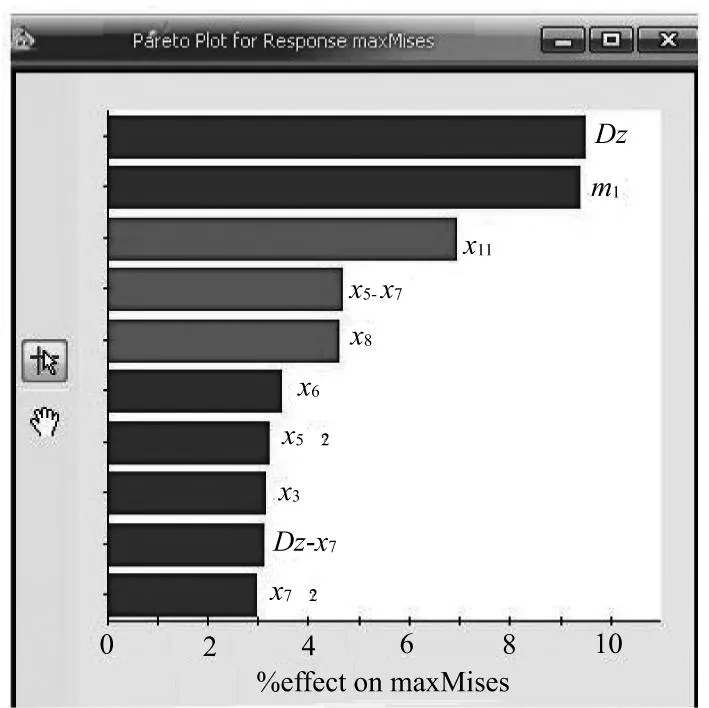
图5　应力影响的Pareto图

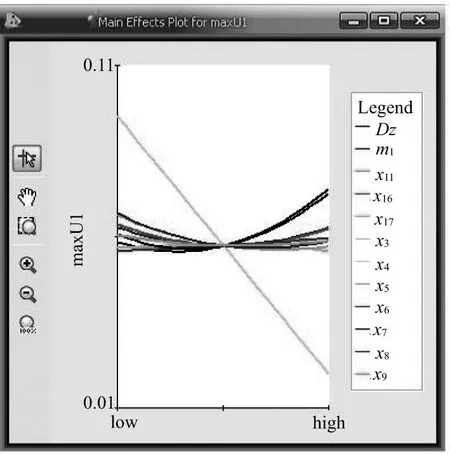
图6　位移影响的主效应图

通过Pareto图可以看出，设计变量对应力影响最大的是导向增压杆直径Dz和位置m1，约占9.4%，其次是x11，占6.9%，然后是x5与x7的交互效应和x8，约占4.6%。设计变量对径向位移影响最大的x3，占21%，其次是x7和Dz，约占5%。通过研究设计因素对响应影响大小的Pareto图和主效应图发现，对响应影响较大的设计因素其本质是影响了火药气体作用效能(如DZ)、锥面角度和初始间隙。综合以上分析结果，决定在设计时尽量增加增压杆外径Dz，减小初始间隙和锥面角度。

3尺寸优化

以8杆密封结构为例，根据灵敏度分析结果确定尺寸优化方案，并且得到密封结构的最优尺寸。根据灵敏度分析结果调整设计参数，密封结构尺寸设计参数如表1所示：

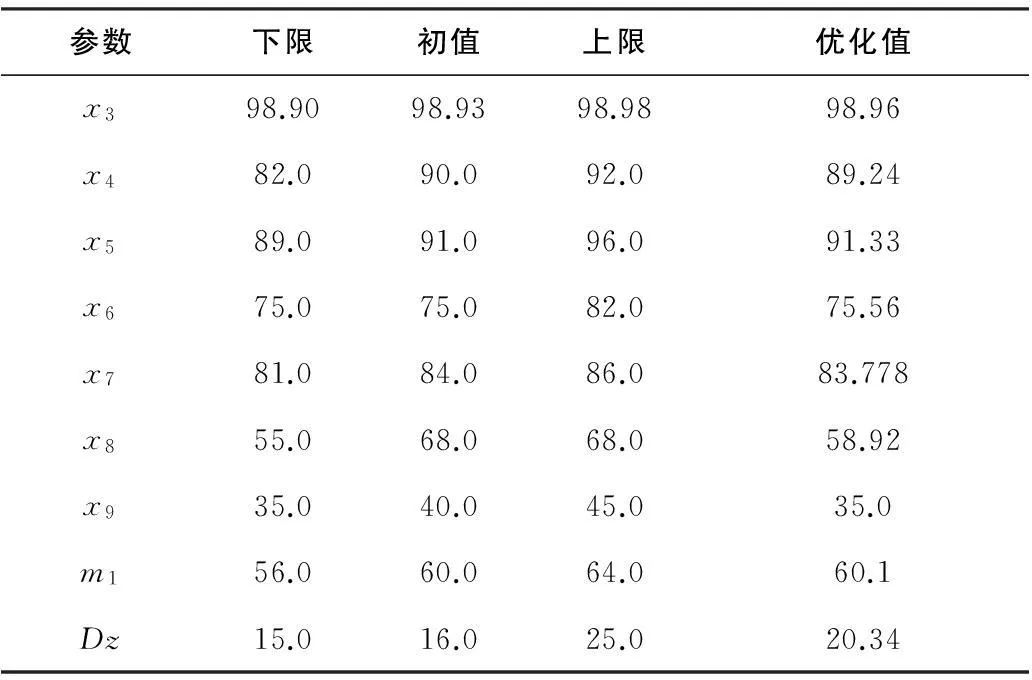
表1　密封结构尺寸设计参数　mm

加载、约束方式、目标函数及设计变量同灵敏变分析时一样。根据表1的优化结果重新设置了各元件的结构尺寸，并对优化后的密封结构重新进行了有限元分析，对比改进前后的结构强度和密封性能。

改进后密封结构最大应力为1138MPa，位置与改进前一样，均在压盖上导向增压杆装配孔根部(图7)。压盖材料屈服强度1350 MPa，强度满足要求。从表2的数据中可以看出，结构改进前密封时间为0.8ms，结构改进后密封时间为1.1ms，密封时间增加了27.3%，性能提升效果明显。

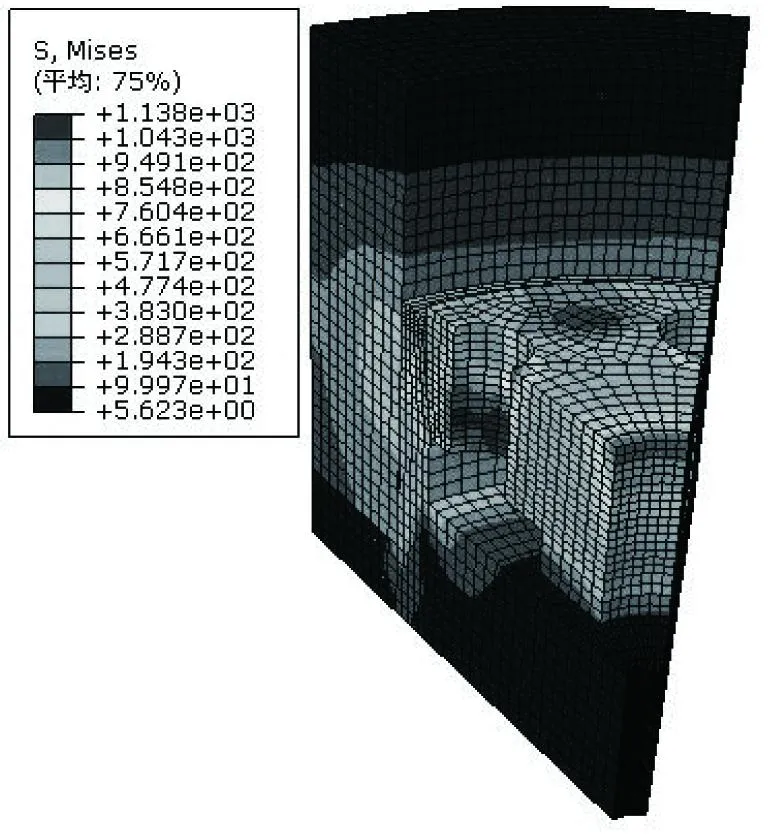
图7　优化后密封结构应力云图

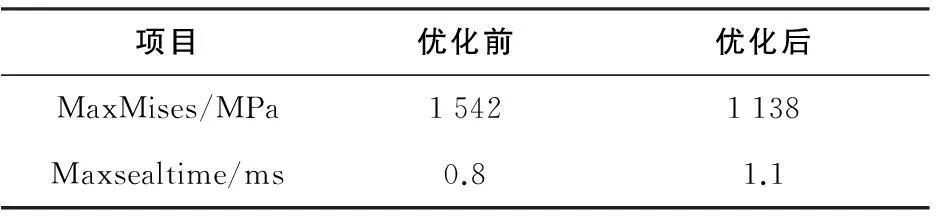
项目优化前优化后MaxMises/MPa15421138Maxsealtime/ms0.81.1

4结论

通过灵敏度分析可以达到两种目的：在众多的设计参数中选择重要的参数实施优化；预先掌握最有利于产品性能的参数变化趋势来指导优化过程。通过对密封结构尺寸的灵敏度分析获得其变化趋势之后，对密封结构进行了重新设计，获得了较优的密封结构，大大提高了设计效率。

参考文献:

[1] 曹金凤, 王旭春,孔亮. Python语言在Abaqus中的应用[M]. 北京:机械工业出版社, 2011.

[2] 白新理. 结构优化设计[M]. 郑州：黄河水利出版社，2008.

[3] 王明真. 轻型火炮大架的优化设计[D]. 南京：南京理工大学硕士学位论文， 2005.

[4] 赖宇阳. Isight参数化理论与实例详解[M]. 北京：北京航空航天大学出版社， 2012.

[5] 兰凤崇, 陈吉清. 承载式车身覆盖件板厚优化及灵敏度分析[J]. 航空制造技术，2005(3): 61-65.

[6] 罗键. 系统灵敏度理论导论[M]. 西安: 西北工业大学出版社，1990.

Optimal Structure Design of Sealing Structure Based on Sensitivity Analysis

CHEN Wei1,2, ZHAO Wei1,3, WANG Cheng4

(1. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;

2. Unit 73841 of PLA, Nanjing 210003, China;

3. Unit75250 of PLA, Guangzhou 510800, China; 4. Unit 94860 of PLA, Nanjing 210049, China)

Abstract:The theory of sensitivity analysis is introduced into a test decice’s sealing structure design. Through the sensitivity analysis of the relevant mechanical data at sealing time and max Mises stress, the design data is decided, which affects the sealing time and stress changes. Meanwhile, according to the results of the sensitivity analysis, the optimal dimensions for the sealing structure are found out. This design concept can provide a reference for optimal data setup.

Keywords:sealing structure; sensitivity analysis; optimal design

中图分类号：TJ303

文献标志码：B

文章编号：1671-5276(2015)02-0011-03

作者简介：陈伟(1986-)，男，安徽阜阳人，硕士研究生，研究方向：高效毁伤。