一类三阶微分方程周期解的变分方法

邓瑞娟

(芜湖职业技术学院，安徽 芜湖 241000)

一类三阶微分方程周期解的变分方法

邓瑞娟

(芜湖职业技术学院，安徽 芜湖 241000)

摘要：运用变分方法探讨了一类三阶微分方程x‴(t)+f(x′(t))+h(x(t))x′(t)+β(t)g(x(t-τ(t)))=p(t)的2π-周期解的存在性，获得周期解存在的一个充分条件，同时推出一个相关推论.

关键词：微分方程；2π-周期解；变分方法

1引言及引理

目前，关于具偏差变元的微分方程的应用越来越多，也使得越来越多的学者开始研究此类方程.由于自然界中很多现象如气候变化、波的振动等都具有明显的周期性，对微分方程解的周期性的研究更具有突出的意义．文[1-3]研究了二阶微分方程解的周期性，对三阶微分方程解周期性的研究虽然也正在进行[4-7]，但是结论相对较少．文[4]研究了x‴(t)+f(x′(t))+g(x(t-τ(t)))=p(t)的周期解；文[5]则给出了x‴(t)+f(x′(t))+h(x(t))x′(t)+g(x(t-τ(t)))=p(t)周期解的相关结论，但是方程

解的周期性，目前仍无法判定．本文利用与文[2，5]相类似的方法，解决了下列三阶微分方程周期解的存在性：

x‴(t)+f(x′(t))+h(x(t))x′(t)+β(t)g(x(t-τ(t)))=p(t)，

(1)

利用重合度理论得到了方程(1)关于2π-周期解的一个新结论.

在方程(1)中出现的f(x),g(x),β(t),τ(t),h(x),p(t)，均为R上的连续函数，特别地，p(t),τ(t),β(t)都是以2π为周期的函数.

(2)

(3)

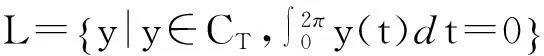
由Fourier级数理论可知，C2π=ImL⊕R，于是codim ImL=dim(C2π/ImL)=1.ImL⊂C2π，且其闭子集，算子L亦是指标为零的Fredholm算子．

假定投影算子P,Q分别为

则ImP=KerL，KerQ=ImL．令LP=L|D(L)∩Ker P，易得LP是可逆的，其逆为

(4)

算子方程Lx=λNx与下列方程等价:

x‴(t)=-λf(x′(t))-λh(x(t))x′(t)-λβ(t)g(x(t-τ(t)))+λp(t)，λ∈(0,1).

(5)

1) 对∀λ∈(0,1)，x∈∂Ω∩D(L)，有Lx≠λNx；

2) ∀x∈∂Ω∩KerL，QNx≠0；

3) deg(JQN,Ω∩KerL,0)≠0，其中J:ImQ→KerL为同构.

2主要结果及其证明

定理1如果方程(1)满足如下条件，其中常数k>0,α≥0,M>0,k1≥0,r>0，

则当4π2(k1+r+β1α(2π+1))<1时，方程(1)至少存在一个2π-周期解．

文化艺术中心以陶瓷作为主要材料，立面装饰采用大量陶板、陶片等元素，彰显福州市打造21世纪海上丝绸之路战略枢纽城市的丰富历史文化。竹子也是主要材料，每个场馆弧形曲线连廊的墙面采用竹皮材料，场馆内部地面、墙面和座椅等也大量使用竹制材料，能有效吸音，减少场馆内的回音。

证明整理方程(5)，得

x‴(t)+λf(x′(t))+λh(x(t))x′(t)+λβ(t)g(x(t-τ(t)))=λp(t)，λ∈(0,1).

(6)

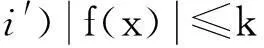
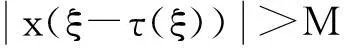
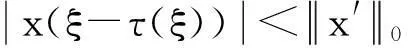
考虑到ξ-τ(ξ)∈R，故一定存在m∈Z，t*∈[0,2π]，使得ξ-τ(ξ) =2πm+t*,于是，故式(6)成立．又因为x(t)，所以

(7)

由iii)知，

(8)

将式(7)、(8)代入式(5)，并结合条件i)，得

(9)

由x(0)=x(2π)知，存在η∈[0,2π]，使得x′(η)=0，因此

(10)

将式(10)代入式(9)，

(11)

再由x′(0)=x′(2π)知，存在η*∈[0,2π]，使得x″(η*)=0，因此

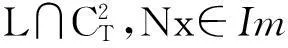
由Mawhin延拓定理知，方程(1)至少存在一个2π-周期解．证毕．

推论1如果存在常数k>0,α≥0,M>0,k1≥0,r>0，使得方程(1)满足下列条件：

则当4π2(k1+r+β1α(2π+1))<1时，方程(1)至少存在一个2π-周期解．

作为应用考虑如下方程：

其中，

由推论1可知，该方程至少存在一个2π-周期解.

参考文献:

[1] 葛渭高．一类n维-Liénard方程的调和解[J]．数学年刊，1990，11A(3)：297-307．

[2] 鲁世平，葛渭高．一类二阶具偏差变元的微分方程周期解[J]．数学学报，2002，45(4)：811-818.

[3] 施吕蓉，周宗福，高伟．一类二阶具多偏差变元微分方程的周期解[J]．山西师范大学学报：自然科学版，2012，26(4)：12-17.

[4] 汪娜，鲁世平．一类三阶具偏差变元微分方程的周期解[J]．安徽师范大学学报：自然科学版，2006，29(1)：17-22.

[5] 刘道金，鲁世平．一类具偏差变元的三阶微分方程周期解[J]．安徽师范大学学报：自然科学版，2010，33(2)：111-115.

[6] 王鲁新，李聚臣．一类三阶具多偏差变元微分方程的周期解[J]．佳木斯大学学报：自然科学版，2009，27(5)：793-796.

[7] 施吕蓉，周宗福，高伟．一类三阶具多偏差变元微分方程的周期解[J]．重庆工商大学学报：自然科学版，2013，30(1)：6-9.

The Variational Method of Periodic Solutions in the Third Order Differential Equation

DENG Ruijuan

(Wuhu Institute of Technology, Wuhu 241000， China)

Abstract:The existence of 2π-periodic solutions for the third order differential equation x‴(t)+f(x′(t))+h(x(t))x′(t)+β(t)g(x(t-τ(t)))=p(t) is explored by the variational methed, a sufficient condition for the periodic solutions is obtained, and a relevant corollary is also provided.

Key words:differential equation; 2π-periodic solutions; variational method

文章编号:1674-232X(2015)06-0652-04

中图分类号:O175.6MSC2010: 34C25

文献标志码:A

doi:10.3969/j.issn.1674-232X.2015.06.016

通信作者：邓瑞娟(1984—)，女，讲师，主要从事微分方程研究．E-mail：5862593@qq.com

基金项目：安徽省自然科学基金项目(KJ2013B347，KJ2013B348);安徽省教育厅高等学校省级质量工程项目(2014mooc070).

收稿日期：2015-04-06