基于分解方法的脉冲型地震动非弹性反应谱分析

赵国臣， 徐龙军， 谢礼立

哈尔滨工业大学(威海)土木工程系，山东威海 264209



基于分解方法的脉冲型地震动非弹性反应谱分析

赵国臣， 徐龙军*， 谢礼立

哈尔滨工业大学(威海)土木工程系，山东威海 264209

本文旨在分析脉冲型地震动中不同频率的地震动分量对于原始地震动幅值及其非弹性反应谱的影响.首先以近期12次大地震的53条典型脉冲型地震动为数据基础，基于多尺度分解方法获取脉冲型地震动中的高频分量和低频分量.为与传统方法对比，本文获取了能够表征地震动脉冲特性的卓越分量及滤除卓越分量的剩余分量.然后对比分析原始地震动和4种地震动分量的幅值特征和非弹性反应谱的特性，以讨论地震动分量对原始地震动幅值参数及其非弹性反应谱的影响.最后结合简谐地震动模型和地震动分量的性质，讨论脉冲型地震动非弹性反应谱诸多特征的产生原因.分析发现，低频分量不仅是控制脉冲型地震动速度和位移幅值的主要因素，其对原始地震动的加速度幅值也具有不可忽略的影响.低频分量也是导致脉冲型地震动非弹性位移比谱偏大以及强度折减系数谱偏小的直接原因，从而造成结构在脉冲型地震动作用下需要具有更大的非弹性位移以及更高的强度需求.

脉冲型地震动；多尺度分解方法；等延性反应谱；非弹性位移比；强度折减系数

1 引言

受断层破裂方向性效应的影响，断层区附近场地地震动的速度时程中有时表现出明显的脉冲特征：高速度幅值、短持时和长周期性(Bray and Rodriguez-Marek，2004).在研究中通常称此类地震动为脉冲型地震动或近断层地震动.震害资料表明，脉冲型地震动对长周期建筑结构的破坏作用非常突出(Hall et al.，1995; Zhang and Iwan，2002).近年来，随着超高层建筑、大跨度桥梁以及海洋平台等长周期结构的大量建造，脉冲型地震动作用已成为重特大工程结构抗震设计必须考虑的内容.丰富的低频分量是造成该类地震动特殊性的重要原因.典型的脉冲特性便是该类地震动特殊性最直观的表现.为系统分析该类地震动的脉冲特性，国内外诸多学者已开展了大量的关于速度脉冲的研究工作.Makris(1997)、Krawinkler and Alavi(1998)、Bozorgnia and Mahin(1998)和Xu等(2006)采用简单的几何函数等效地震动中的速度脉冲.Baker(2007)采用连续小波变换分离速度脉冲，并为区分脉冲型地震动和非脉冲型地震动提出了判别准则.Yaghmaei-Sabegh(2010，2012)、Mollaioli和Bosi(2012)、谢俊举等(2012)采用Baker(2007)提出的方法对该类地震动进行了更为深入的研究.Ghahari等(2010)采用“移动平均值”的分解方法获取速度脉冲，并论证了方法的可行性.赵国臣等(2013)基于多尺度分析理论提出了一种按照频率从低到高的顺序将地震动逐次分解的方法，并用卓越分量作为速度脉冲的简化形式以分析该类地震动脉冲的特性.尽管关于速度脉冲的研究已取得不少成果，但不论是等效的脉冲还是分解得到的脉冲都不足以充分表征该类地震动的长周期特性.由于这些研究通常仅考虑脉冲的影响而忽略高频成分的作用，因而尚不能系统分析该类地震动反应谱的特性.

本文以近期12次大地震的53条典型脉冲型地震动为数据基础，基于多尺度分解方法以1 s周期为界分别获取地震动的高频分量和低频分量，以讨论不同周期的地震动分量对原始地震动的参数及其非弹性反应谱的影响.为与传统研究方法的分析结果进行对比，对能够表征该类地震动中速度脉冲特征的卓越分量及滤除卓越分量的剩余分量也分别进行了分析.此外，文中采用简谐地震动模型作为地震动分量的简化以辅助分析地震动分量非弹性反应谱诸多特征的产生原因.通过讨论5种(原始记录和4种地震动分量)265条记录的幅值特征和非弹性反应谱特性，对脉冲型地震动的工程特性有了一些新的认识，以期能为相关工作的理论研究和工程实践提供参考资料.

2 地震动分量获取方法

在地震动作用下，结构的反应主要由与其自振频率相近的一个频带范围内的地震动分量决定.而脉冲的频率范围较窄，且不同地震动之间脉冲周期的差别较大.因此，脉冲虽在一定程度上能够表征地震动的长周期特性，但并不易于进行系统的分析.为综合分析脉冲型地震动的低频特性及高频特性，本文采用赵国臣等(2013)提出的多尺度分解方将脉冲型地震动分成高频和低频两部分.多尺度分解方法能够按照频率由低到高的顺序将地震动逐次分解.分解得到的分量在频域、时域以及动态响应三个方面均具有较高的精度.若某目标地震动为X，C1，C2，C3，…，Cn是由多尺度分解方法得到的n条地震动分量，其中Ci的频率大于Ci+1的频率，i= 1, 2, 3, … ,n-1.在地震动X和分量Ci之间具有以下3种特性：

2)在频域内，若分量Ci的傅里叶谱的有效频带范围为A，则在频带A内Ci傅里叶幅值谱的幅值近似等于X傅里叶幅值谱的幅值.

3)在动态响应方面，若分量Ci的周期为Ti，则周期为Ti的单自由度弹性体系在Ci和X作用下的动态响应时程相差不大.

由于Ci的频率组成较为简单，为与后文的其他分量区分，本文称这类分量为简单分量.为分析不同频带范围的地震动分量对原始地震动的影响，本文以1 s为界，将周期小于1 s的简单分量的线性和定义为高频分量HFC(High Frequency Component)，将周期大于等于1 s的简单分量的线性和定义为低频分量LFC(Low Frequency Component).在X的n条分量中，若Ci的周期Ti<1，Ci+1的周期Ti+1≥1，则该地震动的LFC=Ci+1+Ci+2+…+Cn，HFC=OGM-LFC.在理论研究和工程实践中，高、低频之间并不具有一个明确的界限.本文的目的是讨论不同频带的地震动分量对原始地震动非弹性反应谱的影响.因此，没有必要过于精确地定义高、低频分量之间的分界点.本文选取1 s作为分界周期并不具有特殊的意义.

图1为采用多尺度分解方法对集集地震TCU103台站地震动分解得到的7条分量的速度时程曲线.其中：OGM(Original Ground Motion)表示原始地震动；PGV表示原始地震动或地震动分量的峰值速度；T表示分量的周期(采用傅里叶幅值谱的峰值周期表示)，下角标对应于分量的编号.赵国臣等(2013)采用卓越分量PC(Predominant Component，与原始脉冲幅值方向相同的且速度幅值最大的分量为卓越分量)作为速度脉冲的简化形式以分析速度脉冲的特性.由图1知，C6为卓越分量.文中称原始地震动减去卓越分量的剩余部分为剩余分量RC(Residual Component).按照上文定义，C4、C5、C6和C7的和为该地震动的低频分量，OGM减去低频分量即为高频分量.由图可知C7的周期已经超过10 s，目前对于这些超长周期分量的可靠性仍存在一些争议.但分解得到的分量在时域、频域和动态响应三个方面均能满足工程的需要，且此类超长周期分量并不是本文的主要分析内容，因此对于这些超长周期分量的可靠性本文将不做过多的讨论.

图1 集集地震TCU103台站地震动及其分量速度时程Fig.1 Velocity time-histories of the ground motion located at TCU103 station during Chi-Chi earthquake and those of its components

3 地震动数据

本文采用来自近期12次地震的53条典型脉冲型地震动作为此次分析的数据.这些地震动记录均是被普遍认可的脉冲型地震动，场地信息详细，断层距均在20 km以内，所有记录均是处于活断层上的浅源地震记录.其中，岩石场地记录共计14条，土层场地记录共计39条.地震及地震动信息见表1.地震动相对于震级、场地和断层距的分布情况见图2.文中采用多尺度分解方法逐条分解该53条地震动，并求取每一条分量的周期，然后根据高、低频分量的定义获取每条地震动高频分量HFC和低频分量LFC，并根据卓越分量的定义获得能够反映地震动脉冲特性的卓越分量PC及滤除卓越分量的剩余分量RC.在后文中将对该265条5种(OGM，LFC，HFC，PC和RC)不同的地震动数据展开系统的分析与讨论，以分析不同频率的分量对原始地震动幅值参数及其非弹性反应谱的影响.

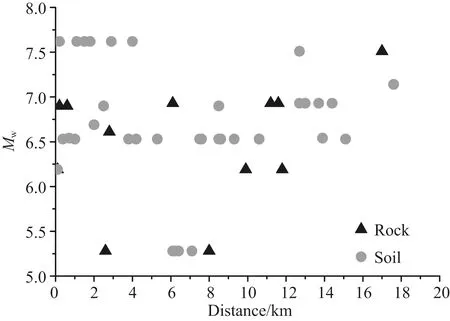
图2 台站分布图Fig.2 Distribution for ground motion stations

4 幅值特征分析

表1 地震动信息表Table 1 Ground motion information

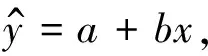
(1)

(2)

(3)

(4)

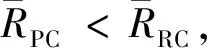
由上述分析知： 1)虽然PC的速度幅值小于LFC和RC的幅值，但PC与OGM之间PGV的相关性系数最大，进一步说明选用PC作为速度脉冲的简化是合理的； 2)HFC与OGM位移幅值之间的相关性很弱，RC因含有部分长周期成分与OGM位移幅值之间存在明显的相关性，所以高频成分对于脉冲型地震动的位移幅值影响很小； 3)PC以及LFC与OGM加速度幅值之间的相关系数大于0.6，且平均比值大于0.3，因此长周期成分对脉冲型地震动的加速度幅值具有不可忽略的影响.

表2 PGA回归分析参数Table 2 Regression analysis parameters for PGA

图3 分量与原始地震动幅值间的相关关系Fig.3 Amplitude correlation between ground motion components and original ground motions

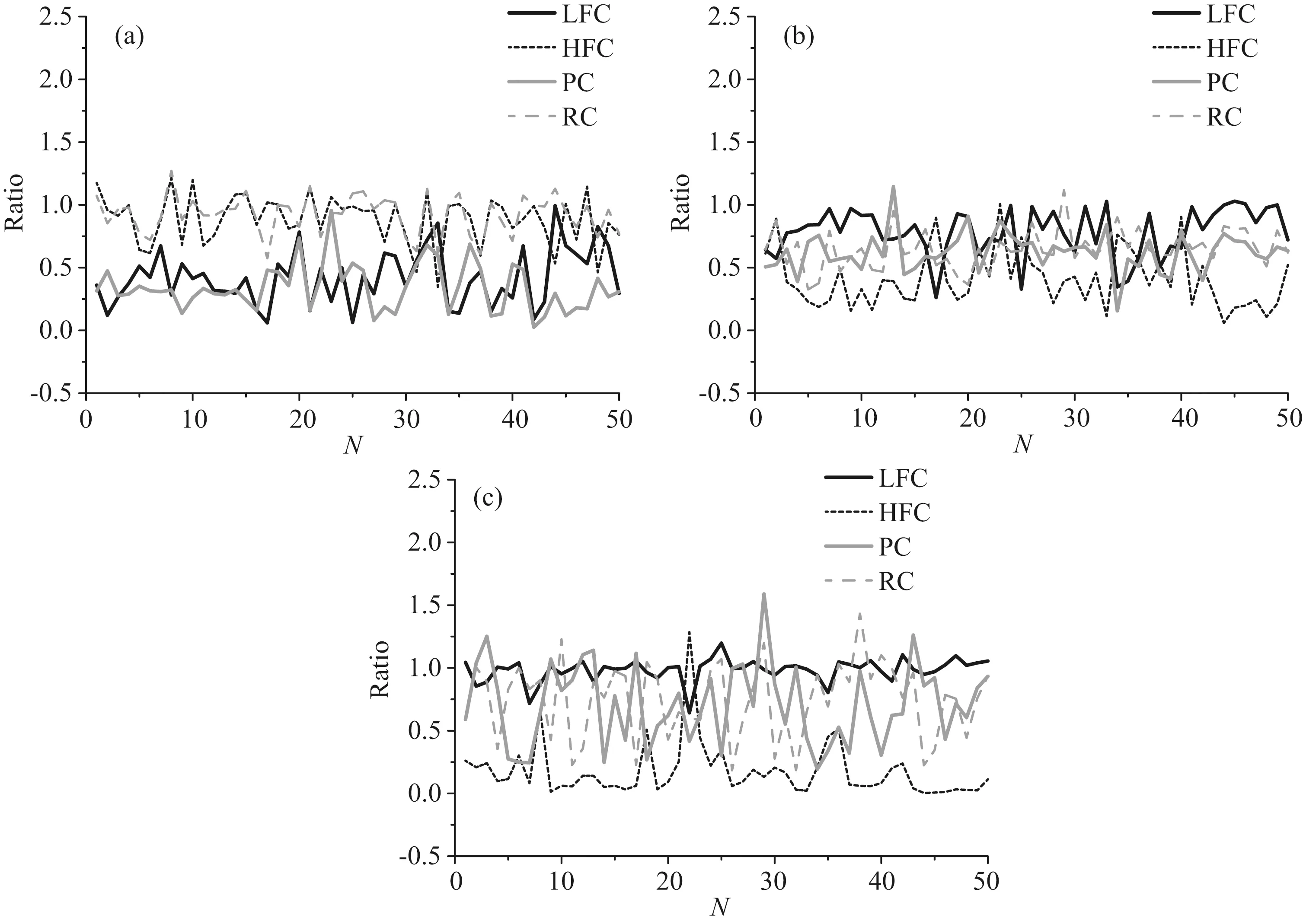
图4 地震动分量与原始地震动幅值间的比值(a) PGAc/PGA; (b) PGVc/PGV; (c) PGDc/PGD.Fig.4 Amplitude ratio between ground motion components and original ground motions

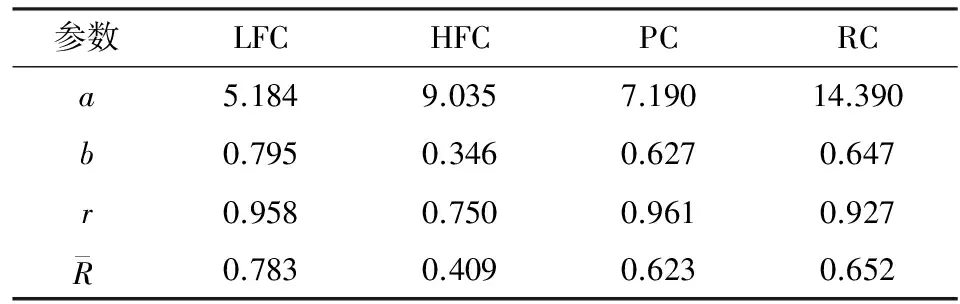
表3 PGV回归分析参数Table 3 Regression analysis parameters for PGV

表4 PGD回归分析参数Table 4 Regression analysis parameters for PGD

5 非弹性反应谱

考虑设计的经济性，结构在较大震级地震作用下不可避免地要进入弹塑性阶段(翟长海和谢礼立，2006).为提高结构抗震设计的精度与计算的准确性，对于非弹性谱的研究至关重要.为探讨不同频率地震动分量对脉冲型地震动非弹性反应谱的影响，本文对比分析了原始地震动和4种地震动分量的非弹性反应谱.在工程实践中，一般采用等延性谱进行新建结构的抗震设计，采用等强度谱评估已建结构的抗震性能.由于篇幅的限制，本文仅讨论等延性反应谱.

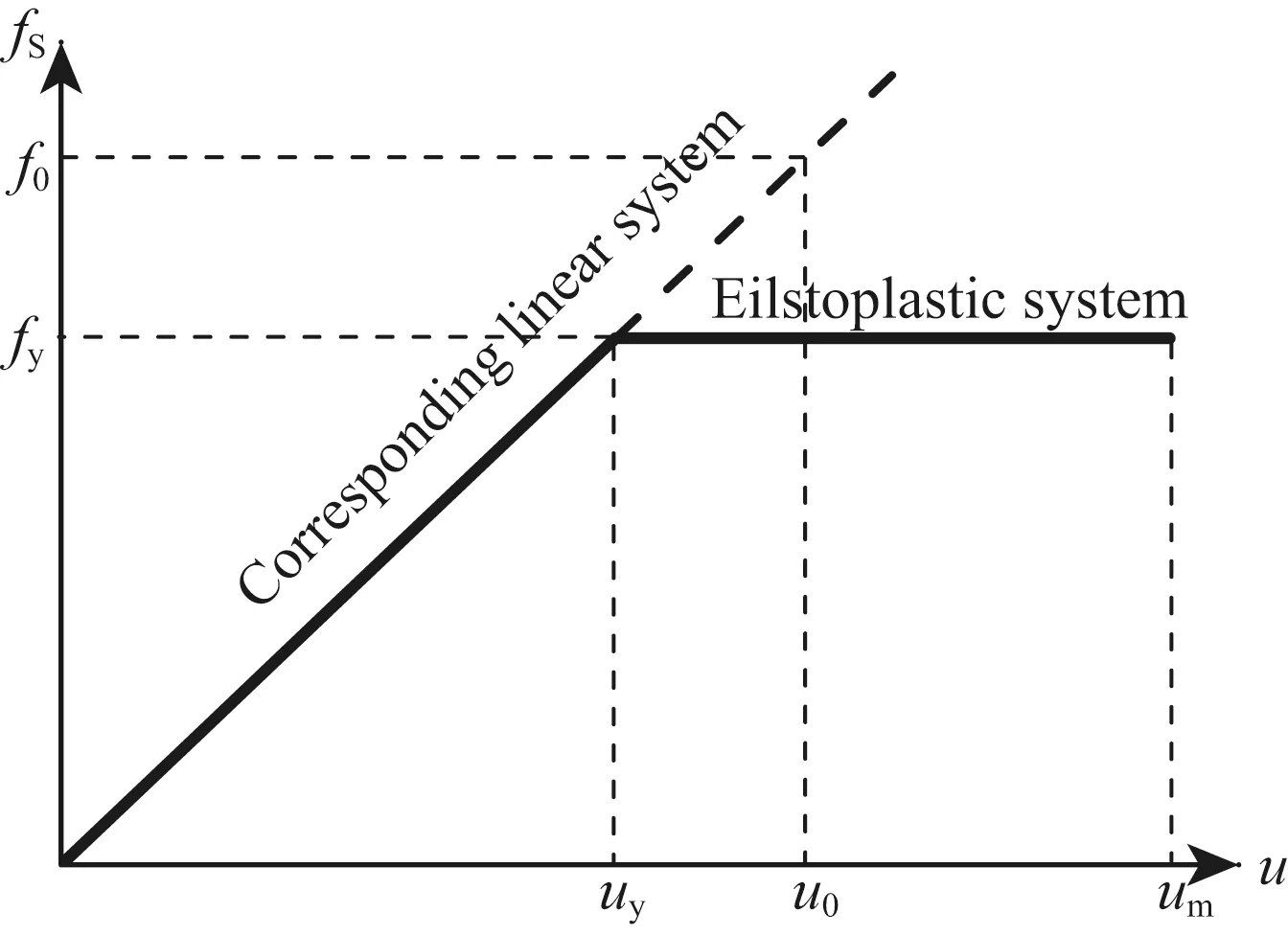
图5 理想弹塑性体系与其相应的弹性体系Fig.5 Elastoplastic system and its corresponding linear system

图5为理想弹塑性体系及相应弹性体系的本构关系图.周期为T的单自由度体系在地震动作用下，体系保持完全弹性时的最大位移反应记为u0，保持完全弹性所需要的最小侧向恢复力记为f0.若体系在该地震动作用下发生塑性变形，其屈服力为fy，屈服位移为uy，最大非弹性位移记为um.一般采用um与uy之间的比值评估结构的延性能力，即延性系数μ=um/uy.结构的最大非弹性位移与相应弹性体系的最大弹性位移之间的比值称为非弹性位移比，即C=um/u0.强度折减系数定义为结构保持完全弹性所需要的最低强度与结构的屈服强度之比.对于图5所示体系，强度折减系数可由f0与fy之间的比值确定，即R=f0/fy.文中计算给定延性目标下的C、R值，即等延性位移比和等延性强度折减系数，分别记为Cμ和Rμ.当体系周期T改变时，将得到新的Cμ、Rμ以及加速度(A)、速度(V)和位移(D)时程峰值.Cμ、Rμ、A、V和D相对于周期T的关系曲线分别称为延性为μ时的等延性位移比谱、等延性强度折减系数谱、等延性加速度谱、等延性速度谱和等延性位移谱.

在计算时，单自由度体系阻尼比取5%，周期介于0.01 s与10 s之间，按照对数坐标等间距取31个周期点；延性系数μ=1, 2, 3, 4, 5, 6, 7, 8；采用图6所示的理想弹塑性恢复力模型，其两个方向的屈服力相同，当|fs|<|fy|时加载与卸载刚度为结构的初始刚度.为得到体系在目标延性状态下的反应，在计算时逐渐降低屈服力fy，直到延性值与目标延性的相对误差(|延性-目标延性|/|目标延性|)小于1%.

图6 理想弹塑性体系力—位移关系曲线Fig.6 Idealization elastoplastic force-deformation relation

6 非弹性反应谱特性分析

6.1 等延性反应谱(加速度、速度、位移)

为讨论4种分量和原始地震动反应谱之间的关系，文中简要分析了5种数据的等延性加速度、速度和位移反应谱(见图7—9).为获得较好的显示效果，图中只给出了μ=1, 2, 4, 8时的反应谱曲线.由图7—9知：在短周期段PC与LFC的谱值均较小，RC和HFC的谱值较大且均与OGM相近；在长周期段PC和LFC谱值较大，且LFC与OGM谱值更为接近；在长周期段HFC谱值逐渐减小，而RC谱值仍较大.此外，可以发现LFC与HFC之间存在明显的交点，在延性系数为1时，交点周期约为1 s，随延性系数的增大交点周期逐渐减小，而PC与RC之间不存在明显的交点.

由上述特征知： 1)PC虽能体现OGM的脉冲特性，但尚不能完全表征OGM的长周期特性，因此其反应谱值在长周期段偏低； 2)RC也不能表征OGM的高频特性，其反应谱值在长周期段偏高； 3)按照本文方法选取的LFC能够充分体现OGM的长周期特性，其反应谱与OGM反应谱在长周期段相差不大.4)在反应谱的短周期段HFC谱值均与OGM谱值相近，且在长周期段谱值显著降低，因此本文选取的HFC能够体现OGM的高频性； 5)由于文中以1 s为界获取LFC和HFC，因此LFC与HFC弹性反应谱之间的交点周期约为1 s，而不同地震动的PC相差很大，且RC中仍含有部分低频成分，因而PC与RC之间不存在明显的交点.

6.2 等延性位移比谱

在基于位移的抗震设计方法中，精确地预估结构的最大非弹性位移是其主要研究内容之一.一种简便且被普遍接受的方法便是采用非弹性位移比评估结构的最大非弹性位移(Ruiz-Garía and Miranda 2003，2006；Ruiz-Garía，2011；Zhai et al.，2013).Veletsos and Newmark(1960，1965)首先采用这种方法分析真实地震动记录和简单脉冲的非弹性位移比谱的特性，并提出了著名的等位移原理.目前，国内外许多学者已开展了大量的关于非弹性位移比的研究工作，并得到了许多有价值的结论.研究发现，脉冲型地震动的非弹性位移比谱大于远场地震动的非弹性位移比谱，表明相对于远场地震动结构在脉冲型地震动作用下需要更大的非弹性位移需求(Chopra and Chintanapakdee，2001).Yaghmaei-Sabegh(2012)对比分析了91条脉冲型地震动和去除脉冲后剩余分量的非弹性位移比谱的特性.研究表明，相对于原始地震动，剩余分量的非弹性位移比谱较小，但没有分析脉冲的位移比谱的特性.

为探讨脉冲型地震动等延性位移比谱诸多特征的产生原因，文中对比分析了原始地震动和4种分量的位移比谱.鉴于单自由度体系在地震动和简单波形荷载作用下的反应之间存在着简单并直接的关系(Veletsos and Newmark，1960)，本文采用徐龙军等(2013)提出的简谐地震动模型作为简单分量的简化.图10是3种模型地震动的加速度时程图.其中，模型1与模型2的振动周期分别为1 s和2 s，加速度峰值为1；模型3是模型1与2的线性叠加，并将其加速度时程同比缩放至峰值为1.由地震动模型的等延性位移比谱(见图11)知，模型2的位移比谱最大，模型3其次，模型1最小，模型1和2位移比谱的最小值点对应的周期与模型的振动周期相等.由集集地震TCU103台站地震动7条简单分量μ=4时的位移比谱知(见图12)，C1～C7分量的谱值逐渐增大，且谱曲线的最小值点与分量的周期近似相等.因此，长周期分量的位移比谱大于短周期分量的位移比谱，简单分量与模型地震动的位移比谱的特征相近.

图7 非弹性加速度反应谱Fig.7 Inelastic acceleration response spectra

图8 非弹性速度反应谱Fig.8 Inelastic velocity response spectra

图9 非弹性位移反应谱Fig.9 Inelastic displacement response spectra

图10 地震动模型加速度时程图Fig.10 Acceleration time-histories for ground motion model

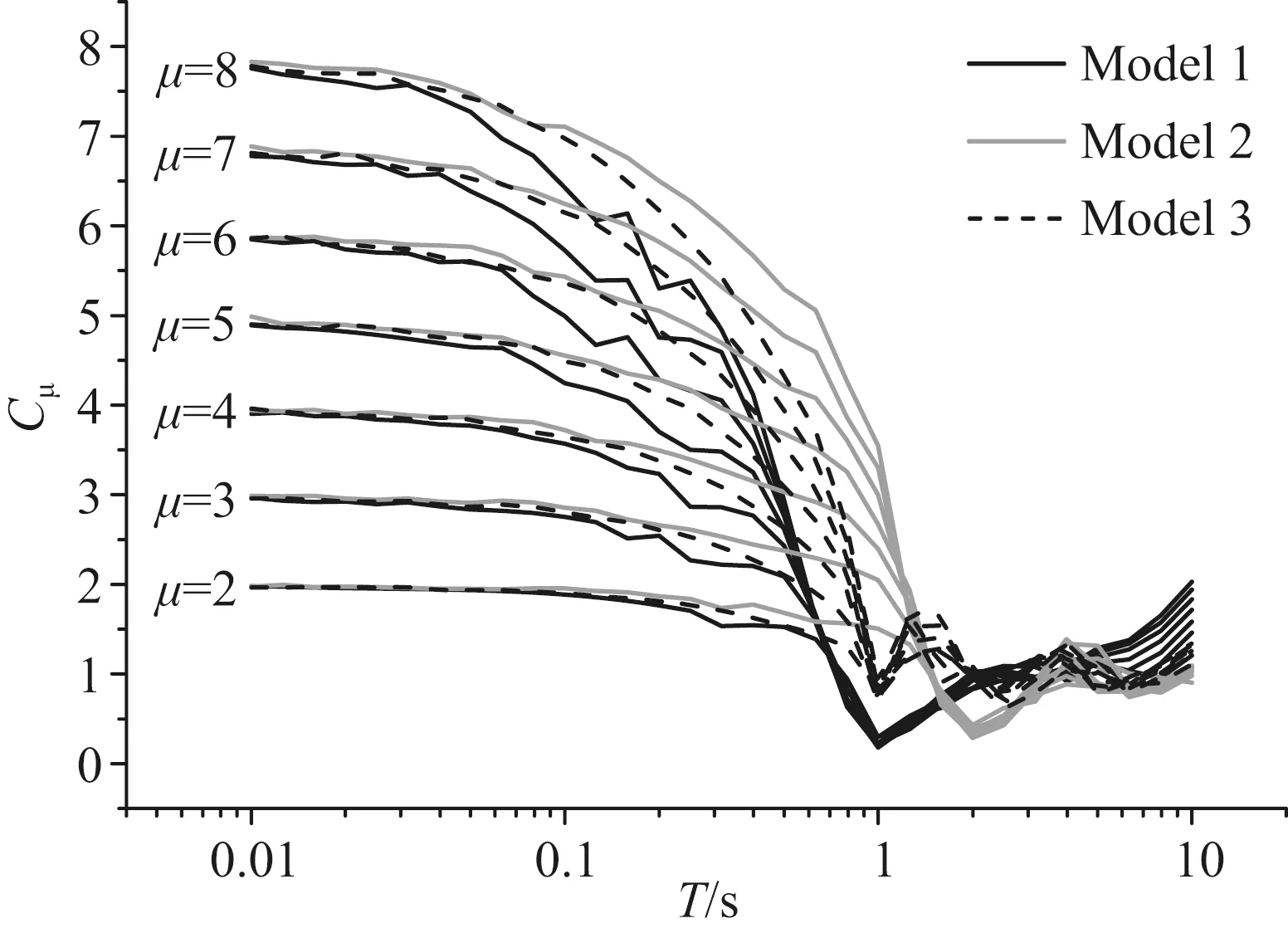
图11 地震动模型等延性位移比谱Fig.11 Constant ductility displacement ratio spectra for ground motion model

图12 集集地震TCU103台站地震动7条分量等延性位移比谱Fig.12 Constant ductility displacement ratio spectra of the 7 ground motions components for the ground motion located at TCU103 station during Chi-Chi earthquake

文中计算了延性系数μ=2, 3, 4, 5 ,6, 7, 8时5种数据的等延性位移比谱(见图13).由图知，HFC与RC的谱值均小于OGM(见图13(a，b))与Yaghmaei-Sabegh(2012)的结论吻合，PC与LFC的位移比谱均大于OGM(见图13(a，b))；由于PC是接近于单一频率的低频成分，且周期较大，而LFC中含有诸多振动周期小于PC周期的成分，故造成PC位移比谱偏大(见图13c)；相对于HFC，RC中仍含有部分长周期成分，故其长周期段的谱值较大(见图13d).

6.3 等延性强度折减系数谱

在基于强度的抗震设计中，为反映地震作用下结构的非弹性滞变特性，一般采用强度折减系数对地震力进行折减.同时，强度折减系数也是基于性态的抗震设计理论中确定非弹性反应谱的主要依据(翟长海和谢礼立，2006).目前关于强度折减系数的研究已有大量的文献可以参考，但对于脉冲型地震动的强度折减系数尚缺乏系统的研究.Chopra and Chintanapakdee(2001)对脉冲型地震动与远场地震动的强度折减系数在加速度敏感区、速度敏感区以及位移敏感区的特性进行了分析，指出，在加速度敏感区脉冲型地震动的强度折减系数明显小于远场地震动的强度折减系数，即在延性状态相同时结构在脉冲型地震动作用下需要更大的强度需求.Gillie等(2010)对脉冲型和非脉冲型地震动的强度折减系数谱进行了分析，其分析结果与Chopra和Chintanapakdee(2001)的研究结果大致相同.这些研究大都是宏观地阐述脉冲型地震动与普通地震动的区别，并未深入探究这些现象的产生原因.本文通过分析地震动分量和简谐地震动模型的非弹性反应谱的特性，以探讨脉冲型地震动强度折减系数谱诸多特征的产生原因.

图13 原始地震动和4种分量(LFC、HFC、PC和RC)的等延性位移比谱Fig.13 Constant ductility displacement ratio spectra for original ground motions and 4 kinds of components (LFC, HFC, PC and RC)

由模型地震动的等延性强度折减系数谱(见图14)知，谱峰值周期与模型的振动周期一致；当体系周期远小于振动周期时，谱值趋近于1；当体系周期远大于振动周期时谱值呈波浪状逐渐变小；虽然模型1与2的加速度幅值一致，但周期较小的模型的强度折减系数谱值较大；模型3是前两种模型的组合，但谱值最小.图15为集集地震TCU103台站地震动7条简单分量的等延性强度折减系数谱.由图知，不同分量的强度折减系数谱峰值周期不同，组合分量(HFC与LFC)的谱值小于单一分量.图16为本文5种数据在延性系数μ=2, 3, 4, 5, 6, 7, 8时的强度折减系数谱.由图知，在短周期段，PC与LFC均小于OGM(见图16(a，b))，PC与LFC差别不大(见图16c).同时，在短周期段(Chopra所指的加速度敏感区)，RC和HFC均大于OGM，与Chopra和Chintanapakdee(2001)中远场地震动和脉冲型地震动之间的特征相似(Gillie et al.(2010)中的非脉冲型地震动与脉冲型地震动).在长周期段，LFC与OGM更为接近.HFC在周期为1s左右时出现一个明显的峰值，且随延性系数的增大峰值愈加明显，而其余数据均未有峰值出现.由上文知，模型地震动与地震动分量的强度折减系数谱也存在峰值(见图14,15).在Chopra和Chintanapakdee(2001)及Miranda(1993)的研究中，其数据的强度折减系数谱也带有明显的峰值.因此，笔者认为OGM、PC、RC和LFC中均包含丰富的长周期成分，故导致其强度折减系数谱峰值后移，且不同频率的分量组合后使峰值不太明显.

图14 地震动模型等延性强度折减系数谱Fig.14 Constant ductility strength reduction factor spectra for ground motion model

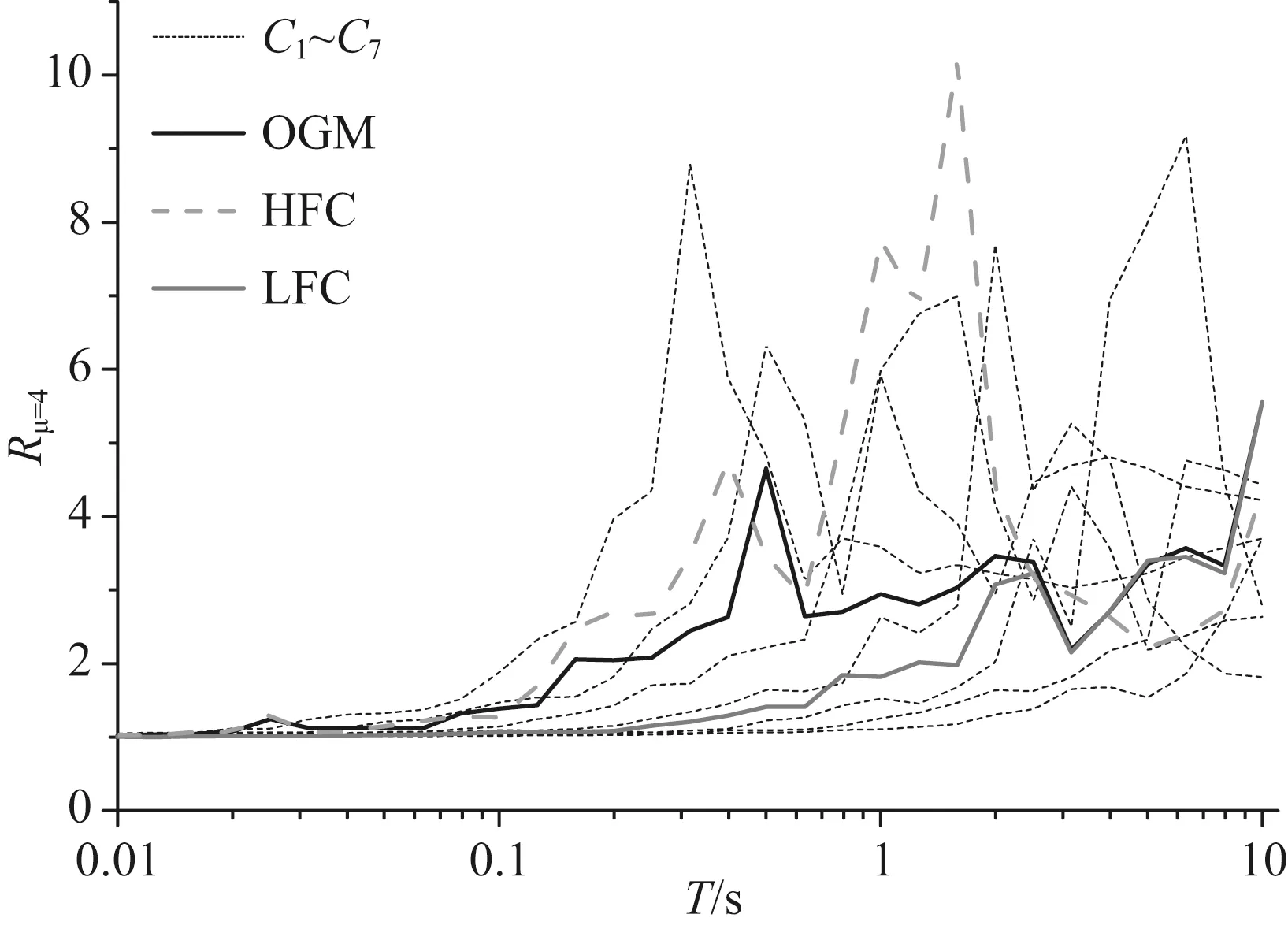
图15 集集地震TCU103台站地震动分量强度折减系数谱Fig.15 Constant ductility strength reduction factor spectra of the components for the ground motion located in TCU103 station during Chi-Chi earthquake

7 结论

本文以近期12次大地震的53条脉冲型地震动为数据基础，基于多尺度分解方法，讨论了原始地震动和地震动分量之间的幅值及非弹性反应谱的关系，对脉冲型地震动的工程特性有了一些新的认识，主要结果如下：

1) 脉冲型地震动的速度和位移幅值主要由低频分量决定，加速度幅值主要受高频分量的影响，但低频分量对其加速度幅值仍有不可忽略的影响，而高频分量与原始地震动位移幅值之间的相关性较弱.

2) 卓越分量不足以充分反映脉冲型地震动的长周期特性，且与其相补的剩余分量也不宜用于表征原始地震动的高频特性.由多尺度分解方法得到的高频分量与低频分量能够很好地分别表征原始地震动反应谱高、低频段内的特性.

3)简单分量和简谐波地震动模型的等延性位移比谱和等延性强度折减系数谱的特征相似，由于简单分量并不是理想的单一频率的简谐波，故造成其谱曲线的光滑度较差.

4) 地震动中的长周期分量是导致脉冲型地震动非弹性位移比偏大以及强度折减系数偏小的直接原因，从而造成结构在脉冲型地震动作用下需要具有更大的非弹性位移以及更高的强度需求.

在传统的研究中一般需要考虑震级、场地和断层距等因素对地震动的影响.本文从分量的角度分析脉冲型地震动的特性，由于受记录数量的限制，本

图16 原始地震动和4种分量(LFC、HFC、PC和RC)的等延性强度折减系数谱Fig.16 Constant ductility strength reduction factor spectra for original ground motions and 4 kinds of components (LFC, HFC, PC and RC)

文尚未讨论震级、场地和断层距等因素对分量的影响.当将来获得足够多的近断层记录时，我们会进行地震动的详细分类并进行讨论，也将另文刊出.

Baker J W. 2007. Quantitative classification of near-fault ground motions using wavelet analysis.BulletinoftheSeismologicalSocietyofAmerica, 97(5): 1486-501.

Bozorgnia Y, Mahin S A. 1998. Ductility and strength demands of near-fault ground motions of the Northridge earthquake. ∥Proceedings of the 6th US National Conference on Earthquake Engineering, Earthquake Engineering Research Institute, Seattle.

Bray J D, Rodriguez-Marek A. 2004. Characterization of forward-directivity ground motions in the near-fault region.SoilDynamicsandEarthquakeEngineering, 24(11): 815-828. Chopra A K, Chintanapakdee C. 2001. Comparing response of SDF systems to near-fault and far-fault earthquake motions in the context of spectral regions.EarthquakeEngineering&StructuralDynamics, 30(12): 1769-1789.Ghahari S F, Jahankhah H, Ghannad M A. 2010. Study on elastic response of structures to near-fault ground motions through record decomposition.SoilDynamicsandEarthquakeEngineering, 30(7): 536-546.Gillie J L, Rodriguez-Mark A, McDaniel C. 2010. Strength reduction factors for near-fault forward-directivity ground motions.EngineeringStructures, 32(1): 273-285.

Hall J F, Heaton T H, Halling M W, et al. 1995. Near-source ground motion and its effects on flexible buildings.EarthquakeSpectra, 11(4): 569-605.

Krawinkler H, Alavi B. 1998. Development of an improved design procedure for near-fault ground motions. SMIP 98 seminar on utilization of strong motion data, Oakland, CA.

Makris N. 1997. Rigidity-plasticity-viscosity: can electrorheological dampers protect base-isolated structures from near-source ground motions?EarthquakeEngineering&StructureDynamitic, 26(5): 571-591.Miranda E. 1993. Site-dependent strength-reduction factors.JournalofStructuralEngineering, 119(12): 3503-3519.

Mollaioli F, Bosi A. 2012. Wavelet analysis for the characterization of forward-directivity pulse-like ground motions on energy basis.Meccanica, 47(1): 203-219.

Ruiz-Garía J, Miranda E. 2003. Inelastic displacement ratios for evaluation of existing structures.EarthquakeEngineering&StructuralDynamics, 32(8): 1237-1258.

Ruiz-Garía J, Miranda E. 2006. Inelastic displacement ratios for evaluation of structures built on soft soil sites.EarthquakeEngineering&StructuralDynamics, 35(6): 679-694.

Ruiz-Garía J. 2011. Inelastic displacement ratios for seismic assessment of structures subjected to forward-directivity near-fault ground motions.JournalofEarthquakeEngineering, 15(3): 449-468.

Veletsos A S, Newmark N M. 1960. Effect of inelastic behavior on the response of simple systems to earthquake motions. ∥Proceedings of the 2nd World Conference on Earthquake Engineering, Japan, vol. 2, 895-912.

Veletsos A S, Newmark N M, Chelapati C V. 1965. Deformation spectra for elastic and elastoplastic systems subjected to ground shock and earthquake motions. ∥Proceedings of the 3rd World Conference on Earthquake Engineering, New Zealand, vol. Ⅱ, 63-682.

Xie J J, Wen Z P, Li X J, et al. 2012. Analysis of velocity pulses for near-fault strong motions from the wenchuan earthquake based on wavelet method.ChineseJournalofGeophysics(in Chinese), 55(6): 1963-1972, doi: 10.6038/j.issn.0001-5733.2012.06.017.

Xu L J, Rodriguez-Marek A, Xie L L. 2006. Design spectra including effect of rupture directivity in near-fault region.EarthquakeEngineeringandEngineeringVibration, 5(2): 159-170.

Xu L J, Zhao G C, Xie L L. 2013. Ground motion response spectra through component decomposition method.JournalofTianjinUniversity(ScienceandTechnology) (in Chinese), 46(11): 1003-1011.

Yaghmaei-Sabegh S. 2010. Detection of pulse-like ground motions based on continues wavelet transform.JournalofSeismology, 4(14): 715-726.

Yaghmaei-Sabegh S Y. 2012. Application of wavelet transforms on characterization of inelastic displacement ratio spectra for pulse-like ground motions.JournalofEarthquakeEngineering, 16(4): 561-578.

Zhai C H, Xie L L. 2006. Study on strength reduction factors considering the effect of classification of design earthquake effect.ActaSeismologicaSinica(in Chinese), 28(3): 284-294.

Zhai C H, Wen W P, Zhu T T, el al. 2013. Inelastic displacement ratios for design of structures with constant damage performance.EngineeringStructures, 53: 53-63.

Zhang Y, Iwan W. 2002. Active interaction control of tall buildings subjected to near-field ground motions.JournalofStructuralEngineering, 128(1): 69-79.

Zhao G C, Xu L J, Xie L L. 2013. On near-fault ground motion characteristics through multi-scale method.ChineseJournalofGeophysics(in Chinese), 56(12): 4153-4163, doi: 10.6038/cjg20131219.

附中文参考文献

谢俊举, 温增平, 李小军等. 2012. 基于小波方法分析汶川地震近断层地震动的速度脉冲特性. 地球物理学报, 55(6): 1963-1972, doi: 10.6038/j.issn.0001-5733.2012.06.017.

徐龙军, 赵国臣, 谢礼立. 2013. 基于分量分离方法的地震动反应谱. 天津大学学报(自然科学与工程技术版), 46(11): 1003-1011.

翟长海, 谢礼立. 2006. 考虑设计地震分组的强度折减系数的研究. 地震学报, 28(3): 284-294.

赵国臣, 徐龙军, 谢礼立. 2013. 基于多尺度分析方法的近断层地震动特性分析. 地球物理学报, 2013, 56(12): 4153-4163, doi: 10.6038/cjg20131219.

(本文编辑 汪海英)

On inelastic response spectra of pulse-type ground motion based on decomposed method

ZHAO Guo-Chen, XU Long-Jun*, XIE Li-Li

DepartmentofCivilEngineering,HarbinInstituteofTechnology,WeihaiShandong264209,China

The inelastic displacement ratio spectra of pulse-type ground motions always have higher spectral values than ordinary ground motions. And the inelastic strength reduction factor spectra of this type motions are usually less than those of ordinary ground motions. That will result in higher displacement and strength demands for building structure when the structure is subjected to pulse-type ground motions. This article attempts to investigate the influence of different frequency components on the amplitude parameters and inelastic response spectral characterizations of pulse-type ground motions.In total, 53 pulse-type ground motions selected from 12 large earthquakes are utilized in this study. And multi-scale decomposed method is adopted to obtain different frequency ground motion components. The frequency content of the ground motion component obtained by the multi-scale decomposed method is very simple. So this type of ground motion component is termed as simple component. To investigate the influence of the ground motion components in different frequency ranges on the original ground motion (OGM), high frequency component (HFC) and low frequency component (LFC) are defined. The HFC is the linear summation of the simple components with the period less than 1s, and the LFC is the linear summation of the simple components with the period no less than 1s. To compare with the results obtained by traditional methods, the predominant component (PC) which can be used as the representation of the dominant velocity pulse and the residual component (RC) which is obtained by removing the PC from original ground motion are analyzed. To explore the reasons for the special characterizations of the inelastic response spectra for pulse-type ground motions, a harmonic ground motion model is used in this study.This article first studies the relationship of the three kinds of amplitude (PGA, PGV and PGD) between original ground motion and the four kinds of ground motion components (LFC, HFC, PC, and RC). Analyses show that the velocity amplitude of PC is less than that of LFC and RC, but the correlation coefficient of the PGV between PC and OGM is more significant. There is a weak relationship of the displacement amplitude between HFC and OGM. Both of the correlation coefficients for PGV and PGD between LFC and OGM are larger than 0.9, but the correlation coefficient of PGA between LFC and OGM is still very large. And then the comparison of the inelastic response spectra between original ground motions and four kinds of ground motion components (HFC, LFC, PC, and RC) is performed. Analyses indicate that the inelastic displacement ratio spectra (IDRS) of HFC and RC are less than those of OGM which is consistent with previous analysis results. The IDRS of LFC and RC is significantly larger than that of OGM. The inelastic strength reduction-factor spectra (ISRS) of PC and LFC are less than those of OGM, and the difference between PC and LFC is not significant. The ISRS of RC and HFC is larger than that of OGM in short-period regions, and the ISRS of LFC is more approximate to that of OGM in long-period regions.The results show that low-frequency component is the major factor that influences the velocity and displacement amplitude of pulse-type ground motion. And it can also cause considerable influence on the acceleration amplitude of original ground motion. Besides, low-frequency component is the immediate causes of the larger inelastic displacement ratio and the smaller inelastic strength reduction factor for pulse-type ground motions.

Pulse-type ground motion； Multi-scale decomposed method； Constant ductility response spectra； Inelastic displacement ratio； Strength reduction factor

国家自然科学基金重大研究计划集成项目(91215301)，国家自然科学基金重点项目(51238012)和面上项目(51178152),山东省科技发展计划(2014GSF122001),山东省蓝色经济区工程建设与安全协同创新中心资助.

赵国臣，男，1990年生，博士研究生，主要从事防灾减灾工程研究. E-mail: zgc011@126.com

*通讯作者徐龙军，男，1976年生，博士，教授，博导，主要从事防灾减灾工程研究. E-mail: xulongjun80@163.com

10.6038/cjg20150828.

10.6038/cjg20150828

P315

2014-03-18，2015-07-04收修定稿

赵国臣，徐龙军，谢礼立等.2015. 基于分解方法的脉冲型地震动非弹性反应谱分析.地球物理学报，58(8):2962-2974,

Zhao G C, Xu L J, Xie L L, et al. 2015. On inelastic response spectra of pulse-type ground motion based on decomposed method.ChineseJ.Geophys. (in Chinese),58(8):2962-2974,doi:10.6038/cjg20150828.